改进PSO-BP算法的压力导丝温度及非线性补偿研究
2016-06-29范广坡余学飞卢广文林良卓周地福
范广坡 余学飞 卢广文 林良卓 周地福
(南方医科大学生物医学工程学院,广东 广州 510515)
改进PSO-BP算法的压力导丝温度及非线性补偿研究
范广坡余学飞卢广文林良卓周地福
(南方医科大学生物医学工程学院,广东 广州510515)
摘要:测量冠状动脉血管血流储备分数的压力导丝中的超微型压力传感器,具有严重的温度以及非线性漂移问题,且目前只有硬件方法进行补偿。针对硬件补偿方法存在的补偿精度不高及成本昂贵等问题,提出一种改进粒子群优化的BP神经网络算法,对压力导丝进行温度和非线性软件补偿。Matlab仿真结果表明,改进PSO-BP神经网络与现有标准PSO-BP算法、BP神经网络等软件以及硬件补偿方法相比,具有成本低、稳定性高、不易陷入局部最优、泛化能力强等优点。
关键词:压力导丝压力传感器温度非线性补偿非线性漂移粒子群算法(PSO)BP神经网络Matlab
0引言
近年来,血流储备分数(fractional flow reserve,FFR)成为评价人体冠状动脉狭窄性病变是否需要介入治疗的“金标准”。Pijls等人将FFR定义为:当狭窄存在时,冠状动脉可获得的最大血流量与正常最大血流量的比值[1-2]。但压力导丝作为FFR测量的核心元件,其远端超微型压力传感器受环境温度以及本身制作工艺的影响,引入温度及非线性误差对FFR测量影响严重。
目前,压力导丝温度及非线性补偿主要有硬件和软件两种方法。本课题组前期进行了硬件方法的补偿研究[3],发现硬件补偿与软件补偿,都存在补偿精度不高且成本昂贵等问题。因此,本文提出一种改进的粒子群算法(particle swarm optimization,PSO)优化(back-propagation,BP)神经网络。使用该算法优化神经网络的权值和阈值,能有效避免BP神经网络易陷入局部最优的问题,提高软件方法的补偿精度、泛化能力和稳定性。
1软件算法补偿原理
软件算法对压力导丝温度及非线性漂移进行补偿的实质,是利用标定的环境压力点、温度点以及在相应环境下压力导丝输出的电压值构成样本数据,通过软件算法拟合出压力导丝测量逆模型,以达到补偿的目的。
温度及非线性补偿原理如图1所示。
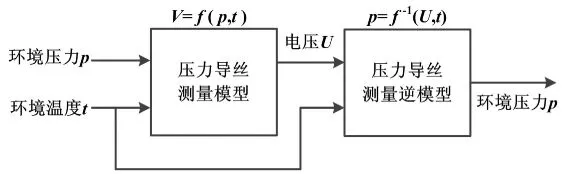
图1 温度及非线性补偿原理图
由图1可以看出,环境压力p和环境温度t经过压力导丝测量模型和改进PSO-BP算法构建压力导丝测量逆模型后,消除环境温度因素以及压力导丝本身非线性因素的影响,进而达到温度及非线性补偿的目的。
2改进PSO-BP神经网络算法
2.1BP神经网络算法
BP神经网络算法是一种带有误差反向传播的多层网络人工智能算法,具有独特的非线性映射能力和很强的环境适应能力,目前应用领域非常广泛[4-5]。软件算法对压力导丝的温度和非线性误差补偿属于非线性系统的拟合过程。现已证明:利用BP神经网络,只要神经元传递函数合适,收敛步数足够多,即可以任意精度逼近一个非线性系统[6]。
BP神经网络训练学习过程的实质,是根据样本实际输出与网络拟合输出之间的误差,利用最小梯度法,不断调整神经网络的权值和阈值等参数,直到训练次数达到最大值或误差达到要求精度,则结束训练,即找到全局最优解。因此,利用BP神经网络对非线性系统拟合时,若非线性系统除了目标极值点外,还有多个其他极值点,训练随机产生不同的初始位置就会得到不同的极小值,即无法找到全局最优解而陷入局部最优。
2.2标准PSO算法优化BP神经网络
PSO算法是一种基于迭代原理的模拟鸟类等动物觅食活动的智能算法,具有实现简单、全局搜索能力强且性能优越等特点。该算法通过群体中个体间的合作寻找最优解[7],寻优过程实质上是对算法优化BP神经网络进行压力导丝非线性补偿,步骤如下。
步骤1:采集压力导丝输出电压以及所处环境相关参数并进行归一化。
步骤2:构建BP神经网络模型,设置网络参数。
步骤3:利用PSO算法优化神经网络的权值和阈值。
①初始化构建粒子群算法,并设置粒子群相关参数。
②计算每个粒子适应度值,并记录每个粒子在历史最优适应度值时的粒子位置pibest,以及粒子群所有粒子在历史最优适应度值时的粒子位置gbest。
③判断最优适应度是否达到要求或迭代次数是否达到最大:若达到,进行步骤④;若未达到,继续步骤④。
④按照以下速度公式(1)和位置公式(2),更新所有粒子的速度和位置:

(1)
(2)
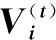
⑤重新返回步骤②。
步骤4:将优化过的权值和阈值赋给神经网络,并判断是否达到神经网络训练要求。若达到,直接进行步骤5;若未达到,对神经网络进行二次优化,达到训练要求后进行步骤⑤。
步骤5:结束BP神经网络训练,完成对非线性系统的拟合过程。
然而,在PSO算法的粒子寻优过程中,粒子运动的速度更新公式会直接影响寻优结果。一般而言,较大的运动速度可以增强PSO算法的全局搜索能力而不至于陷入局部最优,较小的运动速度也可以增强PSO算法的局部搜索能力而不至于跳过最优解。因此,如何平衡PSO算法的全局和局部搜索能力成为PSO算法改进的核心问题。
2.3改进PSO-BP算法
到目前为止,对PSO算法的改进研究已有很多,并且主要集中在对PSO算法的全局和局部搜索能力的平衡上[8-12]。为了进一步提高PSO算法的全局搜索能力,避免陷入局部最优且不错过全局最优,本文一方面综合考虑PSO算法中的粒子适应度以及迭代次数两方面因素,对惯性权重变化进行改进;另一方面对速度更新公式中的rand()项提出增加限值系数的改进方法。
①惯性权重按照下凹函数规律从大到小对数变化[13-15]的同时,综合考虑粒子适应度以及迭代次数两方面因素,达到提高PSO算法搜索能力的目的。惯性权重改进公式为:
ω=ωmax+(ωmin-ωmax)×
(3)
式中:ωmax、ωmin分别为惯性权重的最大值、最小值;t为PSO算法当前迭代次数;tmax为最大迭代次数;k控制下凹程度;fitgoal为目标适应度,fit(i)为当前粒子的适应度。
根据迭代次数和适应度动态改变惯性权重ω,在保证PSO算法前期的全局搜索能力、提高后期局部搜索能力的同时,综合考虑适应度,即离目标位置距离远时增强全局搜索能力、离目标位置距离近时增强局部搜索能力,从而提高了PSO算法的性能。
②首次将对粒子速度更新公式中的随机项rand()添加限制条件的改进方案应用于非线性系统拟合中,当rand()随机产生的系数超出限值系数a时,重新产生一个新的rand()系数。此改进可以在一定程度上限制粒子朝当前最优位置靠近的速度过快,在避免粒子群出现早熟现象的同时,提高粒子群的收敛速度和寻优能力。
③仿真测试。本试验数据来自南方医科大学医工系实验室。所选压力导丝为St.Jude公司的FFR测量导丝,在数字气压计和恒温箱标定的气压和温度下测得试验数据。试验仿真样本数据如表1所示。温度范围根据人体血液情况控制为36~40.5 ℃之间,压力范围根据人体血压范围控制在0~300mmHg之间。测试数据是在采集样本数据的同时,随机记录的非样本温度和压力点处压力导丝的输出。
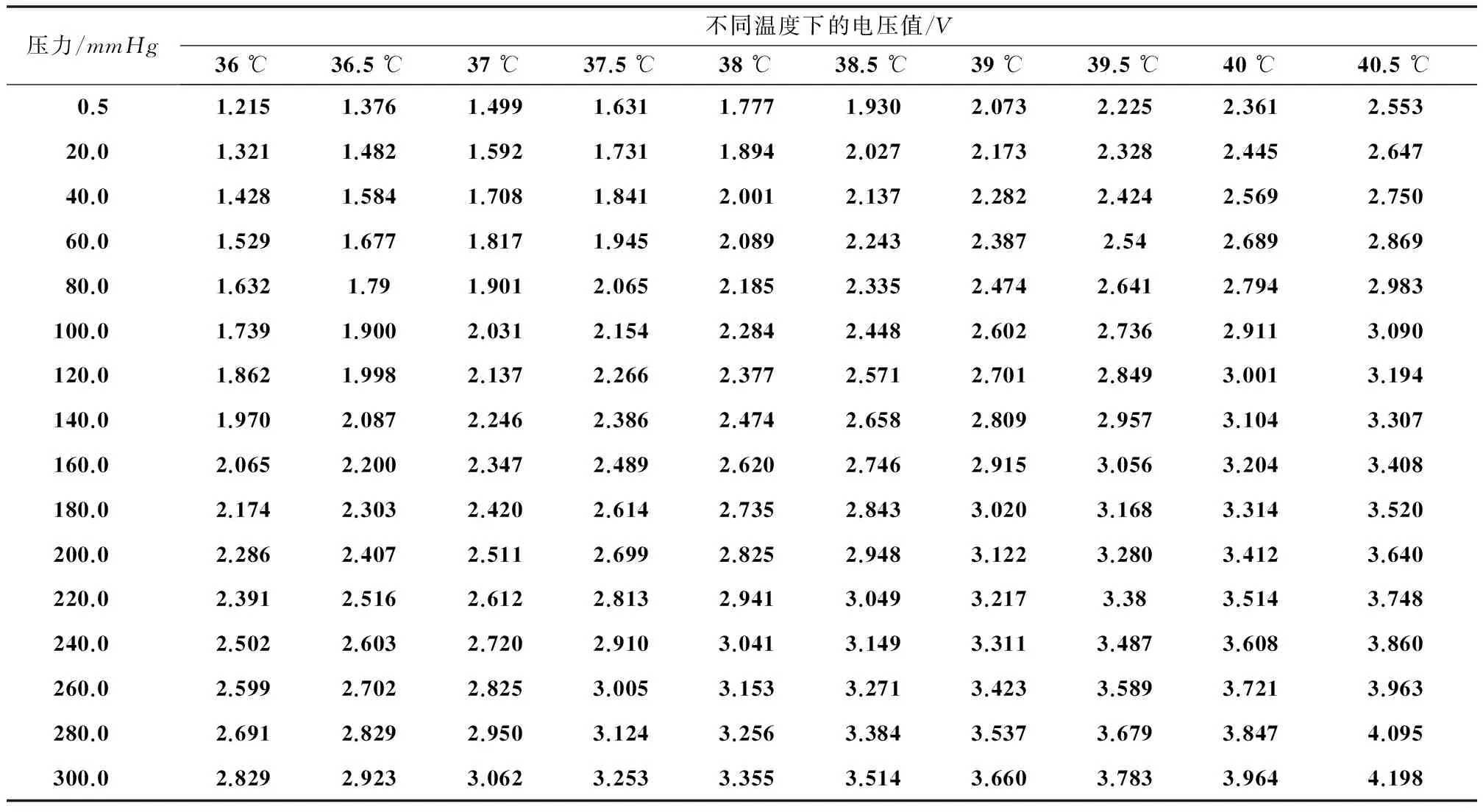
表1 部分仿真样本数据
压力导丝温度及非线性误差如图2所示。为了验证本文提出的改进方案的补偿效果,使用BP神经网络和未改进的PSO-BP算法作对比,通过Matlab仿真软件,利用样本数据对压力导丝测量逆模型进行拟合,比较补偿结果。

图2 温度和非线性误差关系图
隐含层神经元个数与补偿精度关系如图3所示,满足精度要求8×10-6的最少个数为30。
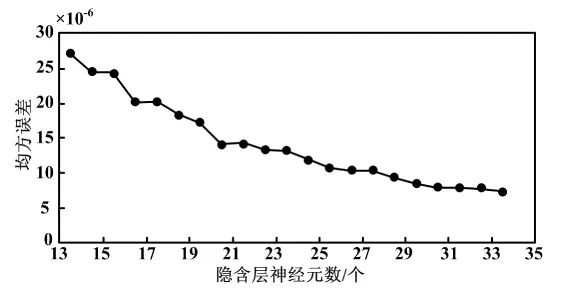
图3 隐含层神经元个数与补偿精度关系图
根据前面所述的步骤,对算法参数进行设定,完成压力导丝的温度和非线性补偿,具体参数设置如下。BP神经网络参数:神经元层数为3层,输入层神经元个数为2,隐含层神经元个数根据图3结果确定为30,输出层神经元个数为1,迭代次数为3 000,精度要求为8×10-6,隐含层传递函数为“tansig”,输出层为“pureline”,网络训练函数为“trainlm”。PSO算法:粒子群种群大小为40,迭代次数为60;惯性权重按照不同的补偿算法设定,ωmax取0.95,ωmin取0.4[13]。
限制系数a取0.2、0.4、0.6、0.8、0.9、1,对粒子群适应度影响如图4所示。当a取0.8时,粒子群寻优能力最好。
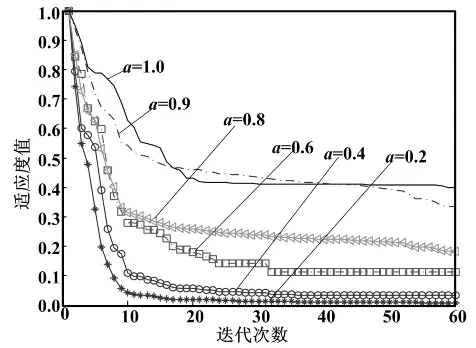
图4 限制系数a对粒子群适应度的影响图
为了验证改进PSO-BP算法的补偿效果,对样本数据分别使用BP神经网络、标准PSO-BP算法和改进PSO-BP算法,进行50次拟合训练,确定了以全局最优解的次数、平均均方误差、最大均方误差和最小均方误差为评判标准。样本数据的补偿结果如图5所示。仿真测试数据如表2所示。利用表2测试数据,验证每次训练拟合出来的非线性系统模型的泛化能力,仿真结果如表3和表4所示。

图5 改进PSO-BP算法补偿效果图
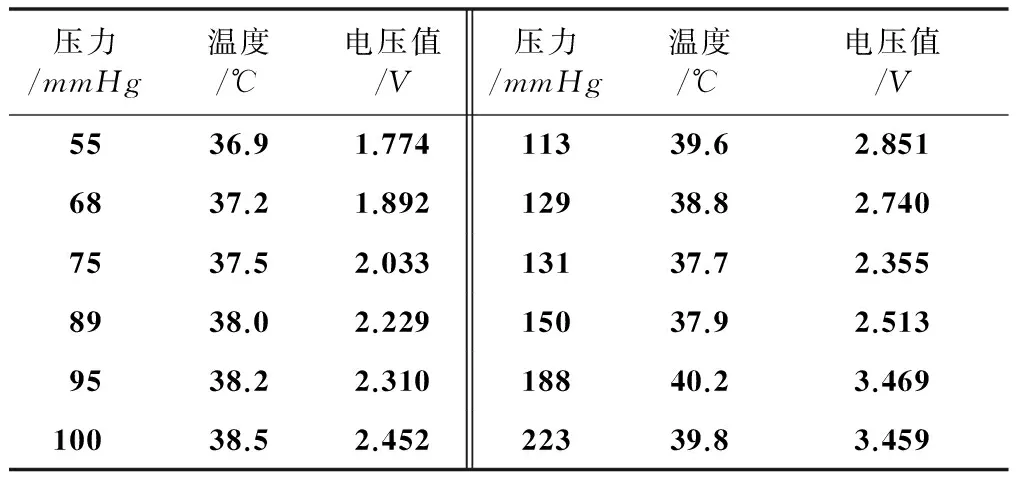
压力/mmHg温度/℃电压值/V压力/mmHg温度/℃电压值/V5536.91.77411339.62.8516837.21.89212938.82.7407537.52.03313137.72.3558938.02.22915037.92.5139538.22.31018840.23.46910038.52.45222339.83.459

表3 样本数据补偿结果

表4 测试数据补偿结果
为了验证改进PSO-BP算法的泛化能力,用测试数据的满量程误差(fullscaleoffset,FSO)来衡量算法预测值与实际压力值之间的偏差,这也直接反映了改进算法拟合非线性系统的泛化能力。仿真结果如图6所示,改进PSO-BP算法拟合出来的结果偏离实际压力值的程度明显低于其他两种算法。FSO定义公式为:
FSO=(Pp-Pt)/(Pmax-Pmin)×100%
(4)
式中:Pp为算法预测压力值;Pt为实际压力值;Pmax为测量范围的最大压力值;Pmin为测量范围的最小压力值。
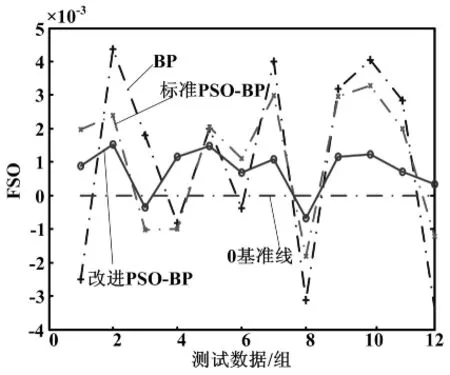
图6 测试数据补偿效果对比图
3结束语
根据仿真测试结果,对比图2和图5可以看出,改进PSO-BP算法有效补偿了FFR压力导丝的温度和非线性误差。同时此改进算法也有效地解决了BP神经网络算法和标准的PSO-BP算法存在的容易陷入局部最优或无法找到全局最优解、稳定性和可靠性有待提高等问题。从表3样本数据补偿结果可以看出,改进PSO-BP算法明显提高了软件算法的补偿精度、稳定性以及可靠性。从表4和图6可以明显看出,改进PSO-BP算法的泛化能力与其他算法相比,也得到了一定程度的提升。综上所述,本文提出的改进PSO-BP算法具有结构简单、参数少、补偿精度高、稳定性好以及泛化能力强等优点,在本项目后续低成本、高精度、高稳定性的FFR测量系统中的压力导丝测量信号温度和非线性补偿上具有很高的应用价值。
参考文献
[1] 王林林,黄进.血流储备分数在冠状动脉介入策略选择中的应用价值[J].心血管病学进展,2010,31(4):521-524.
[2] PIJLS N H J, FEARON W F, TONINO P A L, et al. Fractional flow reserve versus angiography for guiding percutaneous coronary intervention in patients with multivessel coronary artery disease:
2-year follow-up of the FAME (Fractional Flow Reserve Versus Angiography for Multivessel Evaluation) study[J]. Journal of the American College of Cardiology, 2010, 56(3): 177-184.
[3] 余学飞,梁维乐.基于Android的无线血流储备分数实时测量系统设计[J].河南理工大学学报(自然科学版),2014,33(2):202-209.
[4] 王正宏,马以武,陈建群.基于BP网络的厚膜压力传感器非线性校正[J].传感器与微系统,2007,26(2):82-84.
[5] 崔栋,刘敏敏,张光玉.BP神经网络在眼底造影图像分割中的应用[J].中国医学物理学杂志,2011,28(1):2395-2398
[6] 赵辉, 王秀峰.LM算法在传感器数据融合中的应用[J].传感器技术, 2005, 24(5) : 77- 79.
[7] 孙艳梅.基于PSO的BP神经网络在压力传感器温度补偿中的应用[J].传感器技术学报,2014,27(3):342-346.
[8] GENG H, HUANG Y, GAO J,et al.A self-guided particle swarm optimization with independent dynamic inertia weights setting on each particle[J]. Applied Mathematics and Information Science, 2013,7(2), 545-552.
[9] REZAEE J.Enhanced leader PSO (ELPSO): A new PSO variant for solving global optimization problems[J].Applied Soft Computing,2015,26(26):401-417.
[10]孟飞,兰巨龙,胡宇翔.基于改进的量子粒子群优化小波神经网络的网络流量预测[J].计算机应用研究,2014,32(5):1450-1453.
[11]宋明智,杨乐.基于改进自适应PSO算法的WSN覆盖优化方法[J].计算机应用研究,2013,30(11):3472-3475.
[12]郭晓燕,郭民,韩红桂.基于改进型PSO-BP神经网络的SVI软测量[J].控制工程,2014,21(6):873-877.
[13]陈贵敏,贾建援,韩琪.粒子群优化算法的惯性权值递减策略研究[J].西安交通大学学报,2006,40(1):53-56.
[14]LIAO C C,ZHAO X L.Blade layers optimization of wind turbines using FAST and improved PSO Algorithm.Renewable Energy,2012,4(2):227-233.
[15]LING S H,LU H H,LEUNG F,et al.Improved hybrid particle swarm optimized wavelet neural network for modeling the development of fluid dispensing for electronic packaging[J] .IEEE Transactions on Industrial Electronics,2008,66(9):344-346.
Research on the Temperature and Nonlinear Compensation Based on Improved PSO-BP Algorithm for Pressure Guidewire
Abstract:The subminiature pressure sensor in pressure guidewire used for measuring fractional flow reserve (FFR) in coronary artery is provided with serious problems of temperature and nonlinear drifts, and at present, the hardware method is the only way to compensate.Aiming at the demerits existing in hardware compensation method, such as low compensation accuracy and high cost, etc., the improved PSO-BP algorithm is proposed for realizing temperature and nonlinear compensation with software.The results of Matlab simulation show that comparing with hardware compensation method, and the software compensation methods using PSO-BP algorithm, or using BP neural network, the proposed software method using improved PSO-BP algorithm features many merits, including low cost, high stability, strong generalization capability and avoid getting into local optimum.
Keywords:Pressure guidewirePressure sensorTemperatureNonlinear compensationNonlinear driftParticle swarm optimization(PSO)BP neural networkMatlab
通讯作者余学飞(1965-),男,博士,教授;主要从事智能医疗仪器的研究。E-mail:xuefeiyu@smu.edu.cn。
中图分类号:TH811;TP212
文献标志码:A
DOI:10.16086/j.cnki.issn 1000-0380.201606004
广东省科技计划基金资助项目(编号:2012A032200015)。
修改稿收到日期:2015-12-30。
第一作者范广坡(1990-),男,现为南方医科大学生物医学工程专业在读硕士研究生;主要从事智能医疗仪器方向的研究。
