带弹性负载的直流电机试验建模和PID控制

谢树勋　杨　平　于会群,2　郭义波　丁　腾

(上海电力学院自动化工程学院1，上海　200092；同济大学电子与信息工程学院2，上海　200090)

带弹性负载的直流电机试验建模和PID控制

谢树勋1杨平1于会群1,2郭义波1丁腾1

(上海电力学院自动化工程学院1，上海200092；同济大学电子与信息工程学院2，上海200090)

摘要：对多质量弹性扭转电机控制试验装置的扭振特性进行了研究，发现其存在建立数学模型困难和无法保证电机稳定运行等问题，因此，提出了控制性能参数试验建模的计算方法和PID整定的振荡特性对消控制方法。经计算机仿真试验和多质量弹性扭转电机控制试验装置试验证实，所提出的控制性能参数计算试验建模法简单有效，所提出的振荡特性对消PID整定法切实可行，为带弹性负载的电机建模和控制提供了一种解决方法。

关键词：直流电机多质量弹性扭转电机弹性负载辨识PID控制扭转振荡整定仿真风电

0引言

旋转机械装置靠轴传递转动力矩。一般认为，传动轴是刚性的，但在实际应用中，当传动轴细长时，其弹性影响不容忽略。诸如弹性轴类的传动负载被称为弹性负载。文献[1]指出，常见的弹性负载有3类：多质量传动系统(如钢厂的轧机)、有弹性机械联系的多电机传动系统(如宽轨距行车)和弹性张力系统(如带材加工的活套车传动)。弹性负载会带来轴扭振, 影响传动的平稳性。在被控变量弹性振荡严重时，机械部件可能损坏，并导致重大事故发生。因此，传动控制系统必须采取措施来抑制弹性振荡[1]。

对于传动扭振特性及控制方法的研究已受到业内重视。文献[2]针对风电机组设计了含相位补偿环节的、基于电机转速信号的扭转振荡阻尼控制器。文献[3]研究了电动车动力传动系统的扭转特性。文献[4]为解决大弹性负载伺服系统，提出一种基于负载力反馈的变论域双模糊控制算法。文献[5]提出了变增益的方法，来解决具有变刚度弹性负载的电液位置伺服系统的扭转问题。文献[6]采用模糊控制方法，提升变刚度弹性负载液压控制系统的抗弹性扰动能力。

针对多质量弹性扭转电机控制试验装置呈现的典型扭振特性，进行建模和PID控制设计整定研究。试验证明，所提出的试验建模和PID整定新方法是行之有效的。

1带弹性负载的直流电机试验装置

本研究基于贝加莱公司的多质量弹性扭转电机控制试验装置。该系统采用贝加莱X20系列PLC控制器，具体由X20CP1484CPU模块、X20MM2436直流电机控制模块、X20DC1976编码器接收模块和0PS1050.1 24 V 5 A开关电源组成。被控过程由两相空心杯直流有刷电机、减速比14∶1的减速器模块和弹性扭转质量块及光电编码器组成。

多质量弹性扭转电机控制试验装置的系统框图如图1所示。图1中：直流电机控制模块MM2436采用脉冲宽度调制(pulse width modulation,PWM)控制方式来控制直流电机输入平均电压，实现调速驱动功能；计数模块DC1976用来接收编码器的脉冲信号。转速给定信号与转速测量信号相减,得到偏差信号e,通过PLC的PID功能指令,得到PID控制器输出；PID控制器输出作为PWM信号占空比调节的控制信号。PWM信号作用于驱动电路,控制PWM变换器主电路相应桥臂开关管的导通和关断,从而控制直流电机电枢的电压,实现直流电机的PWM调速控制[7]。

图1　弹性扭转控制试验系统框图

2试验建模及仿真验证

为开展带弹性负载的电机控制研究，需要建立被控过程的数学模型。考虑到用机理建模方法存在的实际困难，诸如许多物理参数未知、过程机理不清等因素，采用了试验建模法求取被控过程的数学模型。将直流电机及其弹性负载视为单输入单输出的黑箱系统，通过测量电机弹性扭转系统的输入输出两侧动态过程数据进行系统辨识建模，即利用标准二阶系统的阶跃响应与控制系统性能指标的关系，求取模型参数。

首先，利用自动化工作室(automation studio,AS)系统建立不加控制器的开环控制程序。设置占空比为α=23 000/32 767=70.19%，对应的输入电压U0=24×70.19%=16.85V。运行该开环控制程序并通过AS系统中的Trace模块实时追踪弹簧末端2个质量块的转速数据。所记录的开环阶跃响应曲线如图2所示。

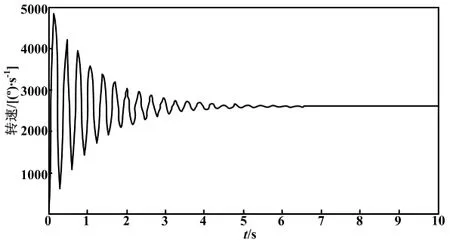
图2　开环阶跃响应曲线

其次，根据图2所示的响应曲线形态，可以假设所求的被控过程为二阶欠阻尼系统，其传递函数模型如式(1)所示。

(1)

第三，在开环阶跃响应曲线图上，可测量出性能指标参数：超调量σp%=87.5%，调整时间ts=4.52s。则根据式(2)所示的关系式，可解出二阶欠阻尼系统参数ξ和ωn，如式(3)所示。又根据式(4)所示的关系式，可解出被控过程的增益K，如式(5)所示。于是，可得二阶欠阻尼的被控过程传递函数如式(6)所示。

(2)

(3)

y(∞)=KU0=2 580

(4)

(5)

(6)

最后，根据式(6)，可利用Matlab作出被控过程的开环阶跃响应仿真曲线。将其与实际的阶跃响应曲线进行对比，结果如图3所示。

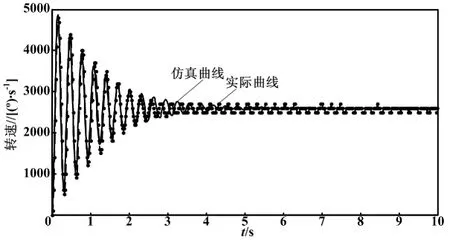
图3　开环阶跃仿真响应曲线与实际响应曲线对比图

图3中，仿真响应与实际响应曲线几乎重合，验证了所建过程模型的有效性。

3PID控制器整定与仿真试验

3.1PID控制器

PID控制器是广泛适用于工程应用背景的控制器，对于电机过程控制也是如此。设PID控制器的传递函数如式(7)所示。

(7)

式中:Kp为比例系数；TI为积分时间常数；TD为微分时间常数。

3.2PID参数整定

经理论分析与试验研究发现，针对如式(6)所示的具有二阶振荡特性的被控过程，常用的几种PID控制器参数整定方法，诸如临界比例度法、1/4和1/10衰减曲线法，均不适用。从所查找的有关带弹性负载的电机控制PID整定的文献看，PID整定仍以人工经验试凑法为主，这也间接印证了常用PID控制器参数整定方法针对衰减振荡特性被控过程的失效状况。因此，需要另辟解决途径。

对于带弹性负载的电机控制系统，最主要的问题就是弹性负载引发持续振荡。为此，控制器设计及整定的最大挑战就是抑制甚至消除振荡。振荡特性对消法是一种新的PID控制器整定方法。其具体方法是先用PID控制器的振荡环节对消被控过程的振荡环节，再根据对消后剩下的过程特性模型整定PID控制器的未定参数。整定计算步骤可分以下2步。

(1)TI和TD的整定计算。

根据式(7)，PID控制器的传递函数可整理成式(8)。令式(9)成立，则有式(10)条件，进而可推导出TI和TD的整定计算式如式(11)。针对式(6)所述的具体过程，根据式(11),得计算结果如式(12)所示。

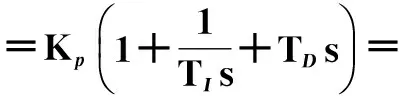
(8)

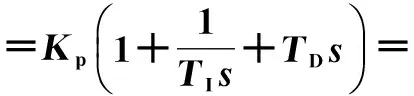
(9)

(10)

(11)

(12)

(2)Kp的整定计算。

当PID控制器的振荡环节对消被控过程的振荡环节后，根据式(9)可知：等效的被控过程G′(s)为积分环节，如式(13)所示；等效的控制器为比例增益为Kp的比例控制器；则等效的闭环传递函数为一阶惯性系统，如式(14)所示，其等效惯性时间T′可用式(15)计算。根据控制理论，一阶惯性系统的输出响应在3T′后可达稳态值的95%[8]。因此，只要设定合理的期望调整时间ts，就可反推出比例增益Kp，如式(16)所示。针对式(6)所述的具体过程，并根据式(16),取值ts=0.04，有式(17)的计算结果。

(13)

(14)

(15)

(16)

Kp=0.002

(17)

3.3PID控制仿真试验

根据式(7)所示理想的完全微分型PID控制器传递函数，当阶跃信号输入时，微分项输出会急剧增加，容易引起控制过程振荡，导致调节品质下降。因此，在PID调节器中加入低通滤波器进行抑制，从而构成不完全微分型PID控制[9]。实际常用的不完全微分型PID控制器传递函数如式(18)所示。

(18)

式中:ε为滤波器系数。

为验证所设计整定的PID控制器是否有效，在Simulink动态系统仿真平台上，搭建仿真试验系统。仿真试验获得的阶跃响应曲线如图4所示。

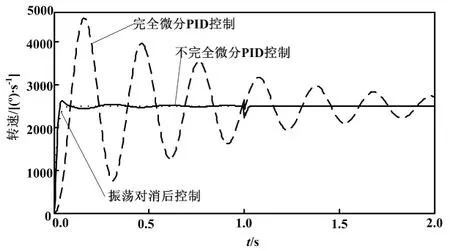
图4　系统闭环阶跃响应曲线

该仿真试验系统包含3个控制回路对比分析，分别是完全微分型PID控制回路、不完全微分型PID控制回路、PID控制器的振荡环节已对消被控过程的振荡环节之后的控制回路。这3个控制回路的输出，都被送入一个示波器进行比较。为观测各控制回路对过程扰动的抑制响应，还在各回路输出处同时加入过程阶跃扰动。阶跃扰动值为500，设置电机设定转速η=2 500 °/s。

从仿真试验结果可以看出，完全微分型PID控制效果(见虚线)最差，超调大且振荡多；不完全微分型PID控制效果(见实线)与理想的振荡已对消后的控制效果(见点线)很接近，控制误差、超调小，扰动抑制强。经研究，完全微分型PID控制效果差的主要原因是纯微分模块的仿真实现误差太大。不完全微分型PID控制得到了消除弹性振荡的预期效果，可用于实际试验。

4实际试验

4.1AS中控制器设置和代码转换

在AutomationStudio软件中，选择PID控制器作为LCRPID控制器。具体设置是d_mode=LCRPID_D_MODE_E；out_mode=LCRPID_MODE_AUTO；Kw=1;kfbk=0。通过对Matlab系统和AS系统的一系列参数进行配置，可使Simulink与AS通信协调，生成植入AS编程环境的启动代码，并下载至贝加莱PCC，以进行硬件仿真和功能测试[10]。

4.2实际控制试验

所设计的带弹性负载的电机控制的实际试验结果如图5所示。

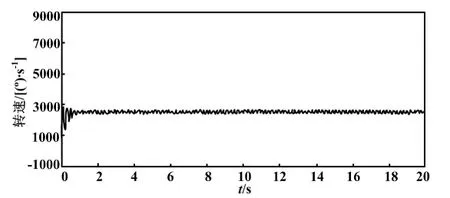
图5　实际试验时的输出转速响应曲线

从图5的转速控制曲线可看出，虽将转速控制在设定值附近，但存在持续的小幅振荡。这可被认为是控制器的振荡特性不能完全对消被控过程的振荡特性的结果。分析不完全对消的原因有两方面：一方面是所建立的模型不够准确，未能反映实际过程全部的动态特性；另一方面是所设计的控制器的振荡特性未能精确实现，比如因为Simulink系统本身存在仿真误差。针对上述原因，其解决方法是建立更准确的模型和提高控制器的实现精度。但是，无论是过程的准确建模，还是控制器模型的准确复现，都已无多少改进空间。因此不妨采用更实用的方法，即人工调整PID参数。这实质上是通过改变控制器的振荡特性，使之与被控过程的振荡

特性相匹配。人工调整PID参数试验的结果是：当在所设计的PID参数基础上，把微分时间减少至TD=0.45s时(同时比例KP增大),可得到消除振荡的实际控制效果，如图6所示。由图6可见，动态过程启动9s后，转速响应曲线已拉直，这说明振荡特性已对消。

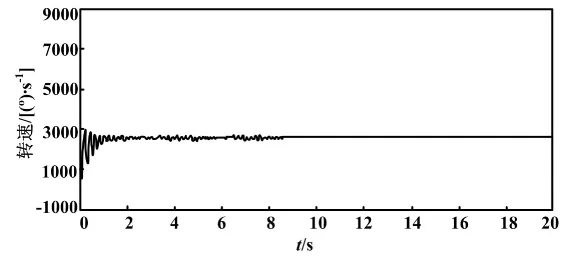
图6　人工调整PID参数试验时的输出转速响应曲线

5结束语

基于多质量弹性扭转试验装置，用阶跃响应试验建模方法建立了电机控制的质量弹性扭转被控过程的数学模型；根据被控过程所具有的二阶振荡特性的特点，设计了不完全微分PID控制器，以衰减弹性系统振荡特性；通过仿真试验和实物平台试验，验证了模型和控制器的有效性，获得了实际可用的控制效果。该设计具有简单有效、实用性强、抗干扰性好的特点，对于实现弹性负载系统的控制具有现实意义，有广阔的应用前景。

参考文献

[1] 马小亮.驱动弹性负载的调速传动[J].电气传动,2008,38(7):3-7.

[2] 王立新,程林,孙元，等.补偿双馈风电机组电磁转矩-转速闭环相位滞后特性的传动轴系统阻尼控制[J].电网技术,2014,38(12):3333-3340.

[3] 王建,梁锐,张立军，等.电动车动力传动系统的扭转特性研究[J].上海汽车,2011(4):3-8.

[4] 周丹,曾富洪,李泽蓉.大弹性负载伺服系统变论域双模糊控制[J].机械工程学报,2014,50(13):165-169.

[5] 陈永新,柯尊忠,翟华.具有变刚度弹性负载的电液位置伺服系统[J].农业机械学报,2004,35(4):155-158.

[6] 赵慧,吴远会.变刚度弹性负载液压系统的模糊控制[J].机床与液压,2008,36(5):88-90.

[7] 何新霞，邢瑞军.基于PLC的直流电机PWM调速系统设计[J].机电一体化,2011(6):29-31.

[8] 杨平,翁思义,王志萍.自动控制原理—理论篇[M](2版).北京:中国电力出版社,2014:87-98.

[9] 陈平.不完全微分型PID控制的应用研究[J].机电技术，2006(4):31-32.

[10]李磊,黄梓瑜,李刚.SimulinkPLCCoder在贝加莱运动控制系统中的应用[J].仪表技术,2011(6):59-61.

Experimental Modeling and PID Control of DC Motor with Elastic Load

Abstract：The torsional vibration characteristics of the experimental device for multi-mass elastic torsion motor are studied, it is found that the establishment of mathematical model is difficult and the stable operation of motor cannot be ensured.The calculation method of control parameters experimental modeling and the cancelation control method of oscillation characteristics of PID tuning are proposed.The tests of computer simulation and multi-mass elastic torsion motor control experimental device verify that the modeling method proposed is simple and effective, and the cancelation PID tuning method proposed is feasible.It provides a solution for modeling and controlling motor with elastic load.

Keywords:DC motorMulti-mass elastic torsion motorElastic loadRecognitionPID controlTorsional oscillationTuningSimulationWind power

中图分类号：TH71;TP273+.1

文献标志码：A

DOI:10.16086/j.cnki.issn 1000-0380.201606002

国家自然科学基金资助项目(编号：61034004);

上海市教育委员会科研创新基金资助项目(编号：12YZ142);

上海市科学技术委员会基金资助项目(编号：14DZ2251100)。

修改稿收到日期：2015-06-18。

第一作者谢树勋(1990-),男,现为上海电力学院电气系统检测与控制专业在读硕士研究生；主要从事电气自动化方向的研究。