一种BUCK变换器的抗扰动控制方法

严宏举　冯全源

( 西南交通大学微电子研究所，四川 成都　611756)

一种BUCK变换器的抗扰动控制方法

严宏举冯全源

( 西南交通大学微电子研究所，四川 成都611756)

摘要：为解决降压变换器中存在多种扰动(如输入电压变化和负载变化等)严重影响输出电压的问题，提出了一种BUCK变换器的抗扰动控制方法。首先，采用变参数PI(VAPI)控制器代替传统PI控制器，作为改进的PI控制方法；然后，设计扰动观测器(DOB)观测参数摄动与负载变化带来的系统扰动，作为补偿量补偿到前馈通道，提高系统的收敛速度与抗扰动能力；最后，通过仿真验证了该算法的有效性。

关键词：降压变换器扰动观测器PI控制复合控制负载变化补偿收敛速度抗干扰能力仿真

0引言

随着科学技术的日新月异，开关电源技术的应用范围越来越广。其不仅应用在移动电源、LED[1]，还越来越多地应用在航空二次电源、工业机械设备以及电力电网[2-3]和高频器等领域。但随着对开关频率和系统复杂性要求的提高，BUCK变换器对输入扰动、负载突变以及参数变化越来越敏感。因此，保证变换器在各种条件下具有良好的稳定性、准确性以及抗干扰能力显得尤为重要。

基于上述考虑，本文拟采用线性控制加扰动观测的复合控制方案来提高系统的性能。这种复合控制器具有以下优点。①更强的抗干扰能力[3-4]。BUCK变换器系统中的非线性因素可以通过扰动观测器进行观测和补偿，从而消除系统内部和外部扰动带来的影响。②更快的反应速度[5]。扰动观测器通过前馈补偿的方式对控制量进行补偿，加快了反应速度。③简化了参调过程[6]。扰动观测器的模型可以根据实际模型来设计，在不明确实际模型的情况下，可以用简单的一、二阶环节来替代；原有的PID控制器可以简化为P+DOB控制器，仅需要一个比例环节的参数即可。④易于实现[6]。由于扰动观测器具有计算量小的优点，即使采用模拟电路来实现也不会很复杂。

1 BUCK变换器控制系统

BUCK变换器原理图如图1所示。BUCK变换器的工作过程可以简单地分为以下2个状态。①Sw开通，电源向负载供电，电容处于充电状态，二极管D处于截止状态，负载电压U=Ug,负载电流按指数上升。②Sw关断，负载电流经二极管D续流，负载电压U近似为0，负载电流按指数下降。当负载电阻不变时，BUCK变换器将可以达到稳态。

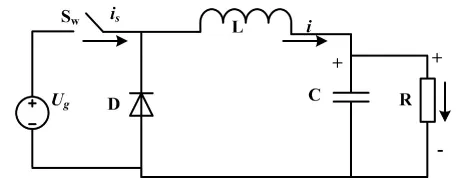
图1　BUCK变换器原理图

根据上述工作过程，先利用空间平均法对BUCK变换器建模，并将时域表达式转化到频域中；然后根据频域传递函数，设计控制器；最后将控制器离散化，得到数字控制器。

在状态①中，Sw开通，D截止，电路工作状态表示为：

(1)

在状态②中，Sw关断，D导通，电路工作状态表示为：

(2)

在低频条件下，将一个周期内的状态①、状态②合并，即将式(1)、式(2)合并，得到：

(3)

式中：d(t)为占空比。

根据式(3)，整理得到状态空间表达式：

(4)

将式(4)进行拉普拉斯变换后，得到状态空间频域的数学模型为：

(5)

由式(5)可知：

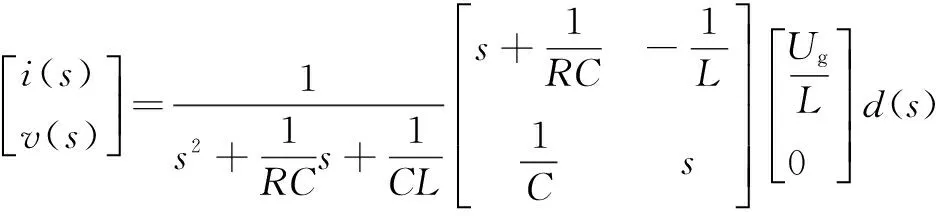
(6)

本文主要讨论电压控制方法，对式(6)进行提取，则得到电压反馈控制的传递函数：

(7)

2复合控制器设计

2.1变参数PI控制器

PI控制器的控制量由期望值与实际输出值之间偏差量的比例(P)与积分(I)进行线性组合所构成。其控制律可以表示为：

(8)

变参数PI(VAPI)控制器继承了PI控制器结构简单、易于实现、计算量小等优点，同时又通过调节过程中参数的自整定，提高了控制效果。传统PI控制器通过选取适当的比例、积分增益，使系统具有一定的动静态性能，这种调参过程往往基于反复试验与一定经验。与传统PI控制器相比，VAPI控制器省去了繁琐的调参过程，采用在线整定的方案，使得系统能够在运行中获得更好的性能。

在系统上升阶段，输出电压U与期望值Uref之间的偏差e的绝对值较大，这时需要较大的比例环节系数KP来加快反应速度；随着e逐渐变小，积分环节系数Ki将变大，这样不仅保证输出电压U无静态误差，超调量也不会因此增大。本文选取的增益为[7]：

(9)

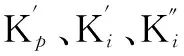
2.2扰动观测器

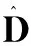
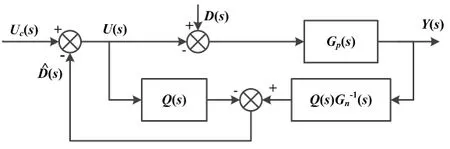
图2　扰动观测器结构图

由式(7)可知，BUCK变换器为二阶系统，其标称模型根据式(7)设计为：

(10)

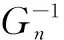
(11)

2.3消除内部扰动的证明

考虑到系统的扰动一般包括输入电压的变化、输出负载的突变以及系统参数的变换，且由于系统参数的不定性，在文中的扰动中选取输入电压和负载这两种来进行推导和证明。

如图2所示，当系统没有扰动时，输出电压为：

Y(s)=Uc(s)Gp(s)

(12)

当考虑输入电压扰动和负载扰动变量时，系统实际的占空比到输出电压的传递函数为：

(13)

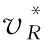
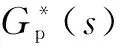
(14)

式中：

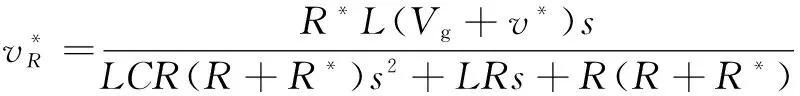
根据式(14),得到系统输出为：

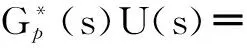
Gp(s)U(s)+G*(s)U(s)

(15)

同时，扰动传递函数为：

(16)

将式(16)代入式(15)，可得：

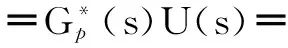
(17)

由于系统输出为：Y(s)=Gp(s)U(s)+D(s)，则：

扰动估计值为：

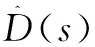
由于Gp(s)=Gn(s)，则：

(18)

又因为补偿后控制量为：

则：

(19)

因此，在模拟添加输入电压和输出负载的扰动后，系统输出为：

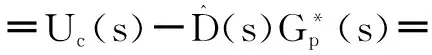
(20)

将式(19)代入式(20)，可得：

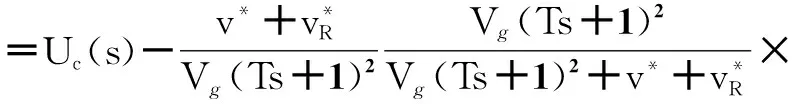
当时间趋向无穷，则有：

因此，在添加扰动观测器环节后，理论上可以消除BUCK变换器的输入电压扰动和输出负载突变。

3仿真验证

利用Matlab2010b内的SimPowerSystems工具包进行仿真验证。电路仿真参数的选取如表1所示。

表1　系统电路参数的选取

根据BUCK变换器的参数，可得被控对象的标称模型的传递函数为:

(21)

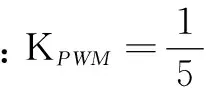
根据实际应用情况，为降压电路设计了2种扰动。图3为3种控制器在负载电阻从25 Ω切换到50 Ω时的输出波形；图4为3种控制器在输入电压正负波动10 V时的输出波形。由图3、图4可以看出，在受到扰动时，加入扰动观测器后输出电压更加稳定、误差更小。

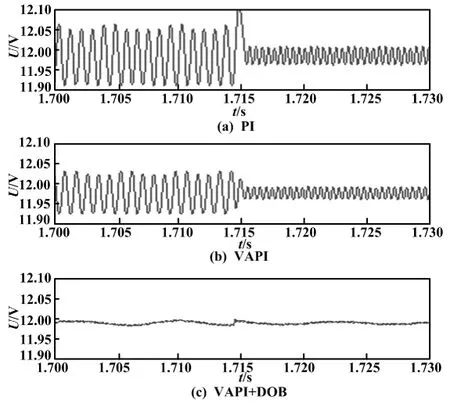
图3　负载突变时输出电压波形图

另外，本文还验证了P+DOB控制器的抗扰动性，输出电压波形图如图5所示。图5(a)反映的是负载电阻在25 Ω与50 Ω之间切换时，输出电压的变化；图5(b)反映的是输入电压在19 V与29 V之间变化时，输出电压的变化。由图5可见，即使只有比例环节，加入扰动观测器之后的系统同样具有较强的抗扰动性。

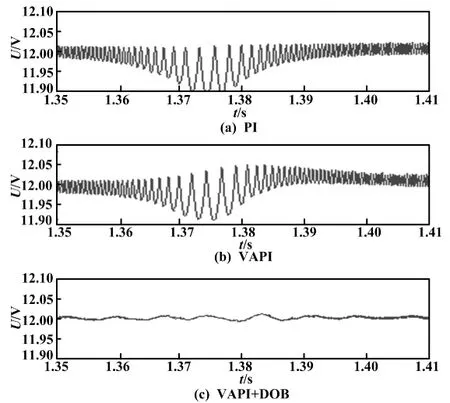
图4　输入电压突变时输出电压波形图

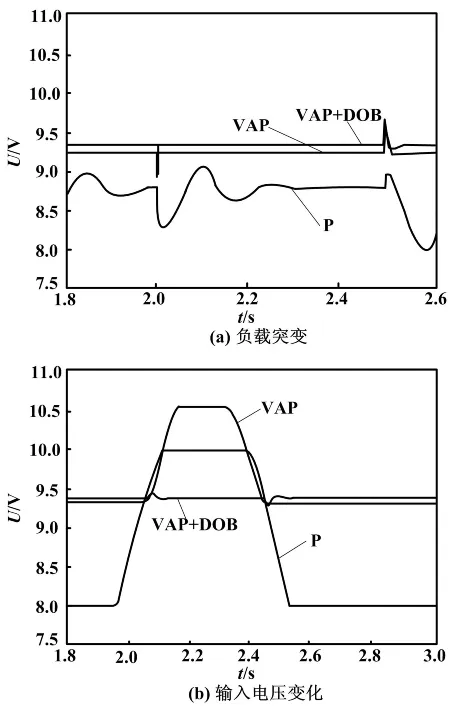
图5　输出电压波形图

4结束语

本文针对BUCK电路的常见扰动，提出了一种基于变参数PI与扰动观测器的复合控制方法。随着数字电源的发展，这类简单、高效的控制算法具有很好的工程应用前景。经过仿真验证，本文所设计的复合控制器有助于提高控制效果与抗干扰能力。

参考文献

[1] 张文煜,刘立群,杨凯.微电网的功率控制系统设计[J].自动化仪表，2014，30(4):1-7.

[2] 孙钦斐，高婷婷，杨仁刚，等.农村户用型智能微电网设计与实现[J].农业工程学报，2013,29(13):150-157.

[3] 马红波,冯全源.BUCK型开关变换器最优PID控制器设计[J].电机与控制学报,2008,12(6):639-643.

[4] 成庶,陈特放,余明扬.开关电源时变模型的新型 PID算法[J].中南大学学报,2007,38(5):970-974.

[5] SALIMI M; SOLTANI J,MARKADEH G A,et al.Adaptive nonlinear control of the DC-DC buck converters operating in CCM and DCM[J].International Transactions on Electrical Energy Systems.2013,23(8): 1536-1547.

[6] BABAZADEH A.Hybrid digital adaptive control for fast transient response in synchronous buck DC-DC converters[J].IEEE Transactions on Power Electronics.2009,24(11): 2625-2638.

[7] SAHIN M E,OKUMUS H I.Fuzzy logic controlled parallel connected synchronous buck DC-DC converter for water electrolysis[J].IETE Journal of Research.2013,59(3): 280-288.

DisturbanceRejectionControlMethodforBUCKConverter

Abstract：In order to solve the problem of a variety of disturbances (variations of input voltage and load changes, etc.) existing in BUCK converter that exerts great influence on the output voltage, the disturbance rejection control method for BUCK converter is proposed.Firstly, the traditional PI controller is replaced by the variable parameter PI (VAPI) controller for improving PI control method; then, the disturbance observer (DOB) is designed to observe system disturbance caused by parameter perturbation or load changes, the observed information serves as the compensation to the feed-forward channel, thus the convergence speed and anti-disturbance capability are improved; finally, the effectiveness of the proposed algorithm is verified by simulation.

Keywords:BUCK converterDisturbance observerPI controlCompound controlLoad variationCompensationConvergence speedAnti-interference abilitySimulation

中图分类号：TH7;TP273

文献标志码：A

DOI:10.16086/j.cnki.issn 1000-0380.201606003

国家自然科学基金资助项目(编号：61271090)；

四川省科技支撑计划基金资助项目(编号：015GZ0103)。

修改稿收到日期：2015-05-29。

第一作者严宏举(1990-)，男，现为西南交通大学微电子学与固体电子学专业在读硕士研究生；从事模拟集成电路设计和滑模控制器设计方向的研究。