大学生数学竞赛题对数学分析课程教学的促进作用*

刘小松

(岭南师范学院 数学与计算科学学院，广东 湛江 524048)

大学生数学竞赛题对数学分析课程教学的促进作用*

刘小松

(岭南师范学院 数学与计算科学学院，广东 湛江 524048)

摘要：以近几届全国大学生数学竞赛数学专业组的预赛题为例，浅析其对数学分析课程教学的促进作用，这无疑将推动数学分析课程的教学改革，从而促进优秀的数学人才脱颖而出。

关键词：大学生数学竞赛题；数学分析；促进作用

全国大学生数学竞赛是一项由中国数学会普及工作委员会举办的全国性赛事，参加对象是大学本科二年级及以上的在校大学生，分数学专业组和非数学专业组，该赛事始于2009年，已举办7届，旨在“为青年学子提供展示数学特长的舞台，也为发现和选拔优秀数学人才积累资源”[1]。现影响日益扩大，参赛人数众多，越来越受到社会各界的关注。本文结合本人多次带队参加全国大学生数学竞赛广东赛区比赛的体会以及近几年全国大学生数学竞赛数学专业组的预赛题，从以下三个方面进行剖析，以期起到“抛砖引玉”的作用。

1竞赛题对数学分析课程概念、性质内容教学的促进作用

以下为首届全国大学生数学竞赛初赛题(数学专业类)的第五题：

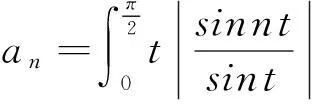
2竞赛题对数学分析课程数学应用内容教学的促进作用

第三届全国大学生数学竞赛初赛题(数学专业类)有下面一道计算应用题(第四题)：对于ΔABC，求3sinA+4sinB+18sinC的最大值。初看此题，以下两个思路很自然，第一易认为这是一道初等数学应用题，用中学的知识和方法即可解决，其实经过一番尝试后，用中学的知识解决非常艰难，且技巧性非常高，计算量大；第二易视该题为典型的条件极值问题，用拉格朗日乘数法求解是常规解法，但经仔细推敲，发现建立的拉格朗日函数有四个变量，稳定点不好确定，且极大值点的判别也不容易。因此，这两个思路只能遗憾地加以放弃。学过数分的人熟知，一元函数的最值问题相对好处理，而且方法也较多，因此，直接将三元函数最值问题化为二元函数最值问题，然后再将二元函数最值问题化为一元函数最值问题，这很可能是一条迈向成功之路。当然，以上想法也有一个难点，就是如何转化? 但利用熟悉的三角恒等式和柯西不等式，发现这个难点是不难突破的。最后，通过一元函数最值问题的常规解法，本题获得圆满的解决。本题的解决给我教学的最大启示是：对一些经典问题，也不能思维定势，退一步可能是海阔天空。另外，这道题也可进一步推广，即将相应三角函数前面的系数一般化(适当加以限制)，我指导的一篇10届本科毕业论文就是从该题出发，得到较为一般的结论。

3竞赛题对数学分析课程计算内容教学的促进作用

首届全国大学生数学竞赛初赛题(数学专业类)有这样一道题：

初步浏览该题，这是一道计算二重积分的题，常规解法是化二重积分为累次积分。由于该题的函数是以微分方程形式给出，是隐函数，而非显函数，直接计算肯定很困难，但从积分域上，很自然想到用极坐标变换比较合适。而利用了极坐标变换后，接下来就是将变换后的二重积分化为累次积分。但化为累次积分，又遇到难关，由于被积函数不是显函数，不能直接用定积分进行计算。但联想到第二型曲线积分可化为定积分后，当然定积分也可化为第二型曲线积分，因此将第一个积分化为第二型曲线积分不失为一个好的办法。最后利用格林公式和已知条件，就将一道二重积分题化为一道先二重后一重的积分问题，这样迂回的好处是最后积分的被积函数“神奇”地变为具体函数，再轻松地利用极坐标变换，就化为熟悉的定积分，求解变为举手之劳之事。纵观该题的解法，极坐标变换起了最关键的作用，把“未知”化为“已知”，化“难”为“易”，不仅是中学数学的常用做法，也为数学分析课程的常用做法。该题也是一道综合题，考察了多个知识点：极坐标变换、二重积分化累次积分公式、第二型曲线积分化定积分公式以及格林公式等。

4结语

全国大学生数学竞赛题数学分析题占整个竞赛内容的50%左右，其综合性，技巧性和新颖性，在参赛学子的脑海里已牢牢地留下印记。本文仅从三个实例剖析竞赛题对数学分析课程教学的促进作用，很可能有遗漏和体会不深刻的地方，但即便如此，这对我开展数学分析课程的教学收益颇丰，主要体现在对数学分析课程概念、性质和计算等教学内容的把握上，对学生逻辑思维的训练上有进一步的感性认识，从而促进数学分析课程的教学。

参考文献：

[1] 张天德，崔玉泉.全国大学生数学竞赛辅导指南[M].北京：清华大学出版社，2014.

[2] 华东师范大学数学系.数学分析(上册)[M].4版.北京：高等教育出版社，2013.

(责任校对谢宜辰)

doi:10.13582/j.cnki.1674-5884.2016.06.010

收稿日期：20160201

基金项目：岭南师范学院2014年精品课程建设项目

作者简介：刘小松(1968- )，男，湖南邵阳人，教授，博士，主要从事多复分析研究。

中图分类号：G642.4

文献标志码：A

文章编号：1674-5884(2016)06-0029-02