关于基因重组中OLC算法的改进研究

买阿丽， 杨雯雯

(运城学院 应用数学系 山西 运城 044000)

关于基因重组中OLC算法的改进研究

买阿丽， 杨雯雯

(运城学院 应用数学系 山西 运城 044000)

针对基因组组装问题，从数据预处理，利用KMP算法在O(m+n)的时间上快速确定某两个碱基片段的最大重复度，将读长序列依据Overlap图连成Contigs链以及ContigsN50的确定4个环节，改进现有的OLC拼接技术，并给出优化后的模型和算法，较好地解决了基因组组装问题.

基因重组； KMP算法； Overlap图； Contigs链； ContigsN50

0 引言

确定基因组碱基对序列的过程，称为测序.目前，测序技术正向着高通量、低成本的方向发展[1-3].但能直接读取的碱基对序列长度远小于基因组序列长度，因此需要利用一定的方法将测序得到的短片段序列组装成更长的序列.

常用的组装算法主要基于OLC(Overlap/Layout/Consensus)方法、贪婪图方法及De Bruijn图方法等[1-2,4].一个好的算法应具备组装效果好、时间短和内存小等特点[5-7].新一代测序技术的性能还有较大的改善空间，曾培龙分析基因组序列拼接所面临的主要挑战，比如大量重复片段的存在，reads数据海量、长度短及含有测序错误等，探讨了当前基因组序列拼接所采用的贪心策略、交叠-排序-生成共有序列(OLC)策略和De Bruijn图策略等，总结了不同算法的优势及不足，提出了序列拼接算法的改进方向，率先在拼接算法中提出了基于信息累计和数据特征相结合的评分方法[4].郑纬名等提出了欧拉超路拼接算法，由于该算法要求构造一个复杂的De Bruijn图,因此用欧拉超路算法拼接大规模全基因组存在存储瓶颈问题[8].王旭提出了一种新的重叠群生成算法SRGA,该算法基于De Bruijn图,将从头测序问题转化成一个四叉树的搜索问题,并采用启发式搜索策略,能够快速地处理海量测序数据,能得到质量较高的重叠群[9].

基因组组装就是将得到的有ATCG4个字符组成的字符串，拼接成更长的字符串，本质上就是字符串匹配问题，利用KMP算法可以较快速地实现基因重组.KMP算法如图1所示[10].本文以2014年深圳杯全国大学生数学建模B题(以下简称2014B题)附件为例在现有的OLC拼接技术上提出改进.2014B题中数据为一个全长约为120 000个碱基对的细菌人工染色体(BAC)，采用Hiseq2000测序仪进行测序，基因组中每个位置平均被测到约70次[11].

1 数据预处理

2014B题得到的长数据存储在fastq文件中，首先将数据读取到Matlab中，并依据以下原则对数据进行筛选，去除不准确的数据.

1) 整条read碱基中无N碱基.N代表模糊碱基，可能是由于测序荧光强度不够造成，将其删除[12].

2) 整条read中质量值低于20的碱基不超过20%.根据文献[12]中给出的公式：字符的ASCII码-64=质量值.也即将read_zhiliang矩阵中ASCII码值中小于84的数据占该行比例小于20%的行删除，对应将reads1、reads2中的该碱基片段删除.

3) 整条read中质量值低于13的碱基不超过10 %.也即将read_zhiliang矩阵中ASCII码值中小于77的数据占该行比例小于10 %的行删除，对应将reads1、reads2中的该碱基片段删除[12].

4) 整条read的碱基平均值不小于20.将不符合的片段删除[12].

依据删除数据的4个标准，reads1共删掉2 805行，reads2共删掉4 487行.得到43 982×89的reads1_used矩阵和42 360×89的reads2_used矩阵，其中第89列记录该行在reads1、reads2中的位置.

图1 KMP算法Fig.1 KMP algorithm

2 建立Overlap有向图

若有两个短片段序列分别为AGTACCTTGCTAGCGT 和GCTAGCGTAGGTCTGA.则有可能基因组序列中包含有AGTACCTTGCTAGCGTAGGTCTGA这一段.事实上，一个片段可能与多个片段都有重复部分，但是重复的碱基数量不同，记此数量为重复度.认为重复越大，这两个片段越有可能连在一起.因此，找到reads1中每个片段与之重复度最大的片段，记下此时的重复度，命为最大重复度.整理这些最大重复度，建立一个Overlap有向图.

2.1 计算两个片段最大重复度

若逐一比较整段基因片段，则需将两个基因片段从不同的位置开始依次比较，这个过程比较复杂，效率很低.因此，在比较两段基因之前先进行查找，快速锁定可能的重复位置，根据可能的重复位置再从最大的可能重复的位置开始比较.以片段a：TCGATACTAG 和片段b：ACTAGGCTAG为例说明.

1) 在b片段中利用KMP算法查找a片段最后3个字符串TAG，称为子串，并记下子串在b中出现的每个起始地址.

3 7

2) 先从位置7开始，倒序向前逐一比较每个字符.

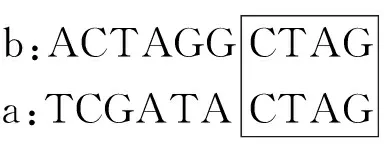
倒序第5位对应不相等，于是再从位置3开始比较.

此时重叠部分相同，重叠部分有5个碱基，认为a、b的最大重复度为5. 称此时子串的起始地址为重复地址，即a与b重复地址为3.

2.2 在多个片段寻找某个片段的后继片段

以a：TCGATACTAG; b：ACTAGGCTAG; c：TAGCCAATTA; d：GATACTAGAC4个片段为例，寻找a的后继片段：

3 7

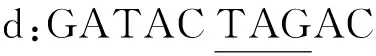
6

1) 用上述1中的方法得出b与a的重复地址为3，最大重复度为5.

2) 在c片段大于等于3的位置上利用KMP算法寻找“TAG”，不是从c的第一个位置开始找，这样就减少了查找次数，提高了执行效率.此例中，发现没有找到.此时仍然认为b最有可能是a的后继片段.

3) 在d片段大于等于3的位置上利用KMP算法寻找“TAG”，发现位置6出现“TAG”,再用2.1中的方法比较d与a，得出重复度为8，大于b与a的重复度，于是认为在b、c、d中d最可能为a的后继片段.

2.3 建立Overlap图算法

Overlap图模型算法1：等长reads重复度计算.

算法描述：对每个ri片段在剩余的片段中寻找后继片段，并计算最大重复度.

算法输入：(1) reads片段集合,即ri集合； (2) 最小重复度d.

算法输出：每个ri片段最大重复度，及其后继片段在ri集合中的序号.

P1初始化,i=1.

P2 若i>n，则结束，否则转P3.

P3 1) 取出ri的最后一个长度为d的子串，记为rd；

2) 令max_p=1及j=1；

3) 若j>n，则转P4；否则转4)；

4) 若j≠i，转5，否则转8)；

5) 令p=max_p；

6) 在ri中从p开始调用KMP算法找到所有子串rd出现的位置，记为B={b-1,b-2,…b-k}其中bi+1>bi,k表示在rd中rj出现的次数；

7) 令l=k,若l<1,则转8)，否则执行以下操作：

① 依次比较rj中第bi之前位置是否与ri中对应字符相等，若直到rj中第一个字符均相等，则令max_p=bi+1，j=j+1，转3).否则转②

②l=l-1，转①；

8)j=j+1，转3).

P4 记录ri的最大重复度为max_p+d-1及对应后继片段rj；i=i+1，转P2.

当rd越大，两个reads片段重复的概率越小，算法执行越快，但会使许多reads无法连接到一起.另一方面，若rd越小，两个reads片段连接的概率越大，算法执行越慢，同时错连概率增大.因此，先取rd=30建立Overlap图，之后对无后继节点取rd=10，完善Overlap图. Matlab编程得到最后的44 042×2的矩阵readsl_used_youxiangtu，第ri行第1列表示第ri个片段的后继片段是rj，第2列表示ri与rj的最大重复度.

3 Contigs的建立

基于 reads 之间的 Overlap 有向图，拼接获得的序列称为 Contigs(重叠群)，Contigs的建立是连接成更长碱基链的过渡环节.

3.1 模型建立

先列举10个片段进行说明，假设这10个片段建立了如图2的Overlap图，第二列表示两个片段的最大重复度.

Overlap图说明：1的后继片段是7，7的后继片段是10，10没有后继片段.所以得出Contigs单链；2的后继片段是3，4的后继片段也是3，3的后继片段是5，5没有后继片段，所以得出Contigs分叉链；6的后继片段是8，8的后继片段是9，9的后继片段是8，所以得出Contigs环链,如图3所示.

产生分叉和环的原因是在整条基因中存在很多碱基序列相同的区域，如图4所示，阴影部分为碱基序列相同的两个区域，虚线是切割位置，与4片段重复度最大的是3片段，于是错把3片段当作4片段的后继片段,因此产生了分叉.环的产生也类似.

实际上，基因中存在许多碱基序列一样的区域，在这种情况下出现分叉和环的概率很大，而且还会出现分叉和环相组合的情况.

图2 10个片段的Overlap图Fig.2 Overlap figure of ten Congtigs

图3 Contigs链Fig.3 Chain of Contigs

图4 有重复片段基因图Fig.4 Figure of duplication Contigs

3.2 数据结构

基于以上分析，为了从Overlap有向图找到Contigs，构造如下的数据结构Contigs.

1) 第i行表示第i条Contigs的信息;

2) 每一行有5个元素，第1列为该条Contigs的起点，第2列为终点，第3列为该条Contigs的类型,0表示单链，1表示分叉，2表示环；

3) 如果为分叉，第4列表示分叉接入的Contigs编号，第5列表示接入的位置;

4) 如果为环，第2列表示接入位置的前驱位置，第4列为0，第5列表示环接入的位置.

3.3 模型算法

Contigs连接算法描述：对建立的Overlap有向图，寻找每一个有向路径，即连接reads片段形成单支、环及分叉.

算法输入：Overlap有向图.

算法输出：Contigs矩阵.

1) 将44 042×2的矩阵reads1_used_youxiangtu对应建立一个44 042×2的矩阵biao_hao，将有后继的节点标记为0，无后继的节点标记为-1，即若biao_hao(i,1)=0表示第i个片段有后继,biao_hao(i,1)=-1表示第i个片段无后继.

2) 找到第1个标号为0的行，记为zerosl，并令Contigs_num=1.

3) 从zerosl之后开始，在矩阵biao_hao中找到第1个标号为0的行，若找到，则该行为第i行，做为第Contigs_num条Contigs的开头片段；令zerosl=i，转4)；否则结束.

4) 在对应到Overlap图中沿后继往后找，同时将经过的每个节点对应的biao_hao改为Contigs_num.

如果节点biao_hao(i,1)=-1，Contigs_num=Contigs_num+1，则转3)；如果节点标号biao_hao(i,1)=contigs_num，则转5)；否则转6).

5) (形成环)记录Contigs中Contigs_num行为环及相应元素值；

6) (形成分叉)记录Contigs中Contigs_num行为分叉及相应元素值；

将形成的矩阵reads1_used_contigs按其类型分为矩阵danzhi_xulie和矩阵fencha_xulie，对形成的环Contigs从接入位置展开，合并到danzhi_xulie矩阵中. Matlab以此算法编程得到矩阵reads1_used_danzhi_xulie.

从矩阵reads1_used_danzhi_xulie中发现有的碱基片段无后继片段，形成单个孤立的片段.单个孤立片段之所以属于矩阵danzhi_xulie，是因为基因被切割后很多碱基序列是完全一样的，这些片断有后继而且彼此之间的最大重复度是88，从接入位置展开后依然是片段本身.对于这些长度仍为88 bp的单链,Contigs将其从矩阵中删除.Matlab编程不断调试后发现rd=10时，即在ri片段中选取倒数10个碱基作为子串，建立Overlap图和Contigs链效果最佳，reads1形成了3 574条Contigs单链，reads2形成3 415条Contigs单链.

Matlab依据Contigs算法编程得到矩阵reads1_used_fencha_xulie，如图5所示.

图5 Contigs矩阵Fig.5 Contigs matrix

对于形成的矩阵fencha_xulie，会形成比较复杂的情况，但都嫁接在单链上， 考虑选取一簇中最长的一条，Matlab编程实现找到每簇分叉中最长的单链，最后将reads1形成的3 574条和reads2形成的3 415条单链分别存入矩阵reads1_contigs_max_dazhi和reads2_contigs_max_dazhi中，再将其转为字符串碱基存入Matlab软件cell中，其中一条长度为282 bp的reads1_contigs碱基,如图6所示：

图6 单链Contigs Fig.6 Single stranded Contigs

图7 碱基片段Fig.7 Basic group

如图7, reads1、reads2是同一基因碱基片段互补链上的碱基，但reads2与reads1的测序方向相反，故将reads2形成的单链Contigs中的碱基先倒序然后再依据碱基互补原则(与碱基A结合的碱基必为T，与碱基C结合的碱基必为G)翻译，并与reads1形成的单链Contigs合并，形成一个总共含有6 989个Contigs链的Contigs库，对所有Contigs链进行一次Overlap图和Contigs链建立，最终在10重复度下形成1 500条Contigs链.

4 ContigsN50的确定

4.1 结果分析

reads 拼接后会获得一些不同长度的 Contigs.将所有的 Contigs长度相加，能获得一个 Contigs 总长度.将所有的 Contigs 按照从长到短进行排序，再按照这个顺序依次相加，当相加的长度达到 Contigs 总长度的一半时，最后一个加上的 Contigs 长度即为 ContigsN50.举例：Contigs1+Contigs2+ Contigs3+Contigs4=Contigs 总长度的1/2 时，Contigs4 的长度即为 ContigsN50[3].ContigsN50 可以作为基因组拼接的结果好坏的一个判断标准.

4.2 ContigsN50的确定

统计得到的1 500条Contigs链的长度，所有长度相加得到Contigs的总长为371 311 bp，将所有的 Contigs 按照从长到短进行排序，将这Contigs的长度从大到小依次累加，最终加到第462条Contigs时，达到总长的一半，第462条Contigs长度为284 bp，所以ContigsN50=284 bp，最长Contigs为1 226 bp .ContigsN50和最长Contigs的碱基序列如图8、图9所示.

图8 ContigsN50的碱基序列Fig.8 Base sequence of ContigsN50

图9 最长Contigs的碱基序列Fig.9 the longest base sequence of Contigs

5 模型计算时间

Overlap图的运行时间：在子串最大重复度为30的情况下，对于reads1和reads2建立Overlap图的运行时间分别在9 638.8 s、9 416 s；最大重复度为10的情况下， reads1和reads2分别在1 283.4 s、1 336 s建立了Overlap图.

r1_r2_Contig的运行时间：重复度30运行时间为498.71 s;重复度10运行时间为485.701 s.

6 结语

对于海量的碱基片段，对数据依据相关文献进行预处理，可以有效避免错误数据对后续拼接的干扰.处理中人工干预较少.在传统的OLC算法上，运用KMP算法将原本的O(m×n)时间缩短为O(m+n)，在保证准确性和连续性不会降低的情况下提高了碱基段的拼接速度.进一步拼接形成3种Contigs链，对于单链和环给出了解决方法，但是出于拼接完整性的考虑，对分叉型Contigs处理还需进一步研究，另外重复度的选取也需进一步探讨.

[1] 骆志刚,方小永，丁凡.DNA 序列拼接的研究进展及挑战[J].计算机工程与科学，2007，29(8):127-127.

[2] 孙海汐，王秀杰.DNA测序技术发展及其展望[J].科研信息化技术与应用，2009(3):18-18.

[3] 徐魁,陈科,徐君,等. CGDNA:基于簇图的基因组序列集成拼接算法[J].计算机科学, 2015, 42(9):235-239.

[4] 曾培龙.基于 reads 引导的基因组序列拼接算法[J]. 智能计算机与应用，2015, 5(3)：23-25.

[5] 汪勇,张新,徐琼,等.基因重组算法设计及多目标旅行商问题求解[J].系统工程, 2015(2):68-73.

[6] 耿丽,张仁杰.对基因组组装算法的分析和研究[J].世界最新医学信息文摘,2015(88):169-170.

[7] 毛华, 赵小娜, 史田敏,等. 多部图的最大匹配算法[J]. 郑州大学学报(理学版), 2013, 45(1):27-29.[8] 郑纬民，林皎，罗水华.DNA 序列拼接中欧拉超路算法的新并行策略[J].计算机学报,2006，29(1): 139-139.

[9] 王旭.基于De Bruijn图的DNA contig生成算法[D].哈尔滨:哈尔滨工业大学,2011.

[10]严蔚敏.数据结构(C语言版)[M].北京：清华大学出版社,2007.

[11]数学建模全国组委会.全国大学生数学建模竞赛[EB/OL].[2014-04-19]. http：//www.Mcm.edu.cn.

[12]美吉生物网.Illumina测序reads过滤[EB/OL]. [2014-05-19]. http：//www.majorbio.com.

(责任编辑：方惠敏)

The Improvement and Research about the OLC Algorithm in the Genetic Recombination

MAI Ali， YANG Wenwen

(DepartmentofAppliedMathematics,YunchengUniversity,Yuncheng044000,China)

It was great significance to obtain the genetic information of the organism quickly and accurately, then to obtain the sequence information of target creature genome for life science research. For genome assembly problem, four steps were proposed .They were the data preprocessing, the use of KMP algorithm in the time ofO(m+n) to quickly determine the maximum of certain segments of two bases the duplication, Contigs chain according to the Overlap figure, and the determination of ContigsN50. They could considerably improve existing OLC splicing technology. The optimized model and algorithm was presented, and the problem of the genome assembly could be solved in an easy way.

genetic recombination; KMP algorithm; Overlap figure; the chain of Contigs; ContigsN50

2015-11-17

国家自然科学基金资助项目(11526183);山西省基础研究项目(2015021015);运城学院数学学科研究项目(XK-2014035, XK-2014030);运城学院博士启动项目(YQ-2014011).

买阿丽(1981—),女,山西运城人,副教授,博士,主要从事微分方程理论及应用研究,E-mail: maialiy@126.com.

买阿丽，杨雯雯．关于基因重组中OLC算法的改进研究[J]．郑州大学学报(理学版)，2016，48(2)：34-39．

Q784

A

1671-6841(2016)02-0034-06

10.13705/j.issn.1671-6841.2015266