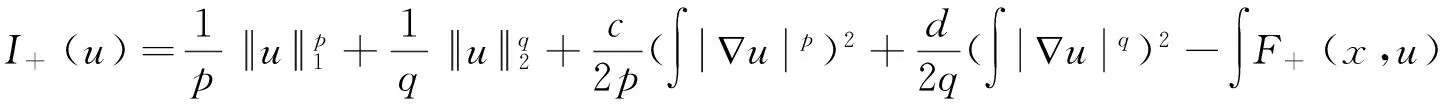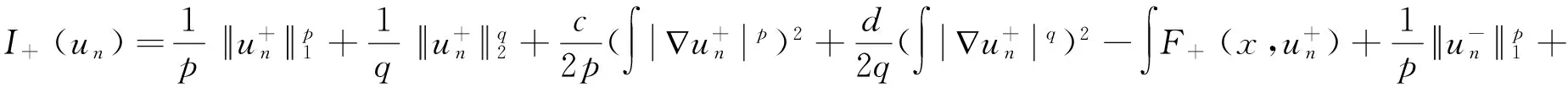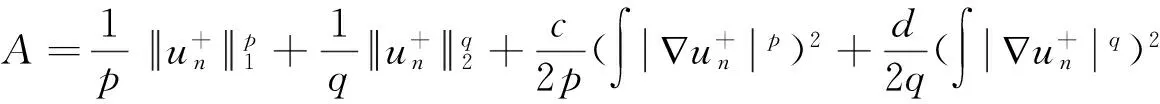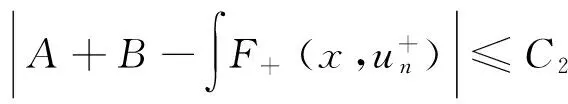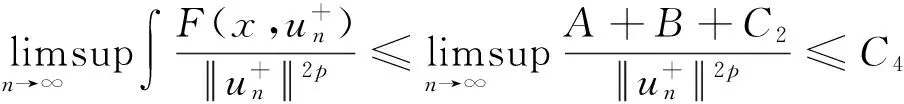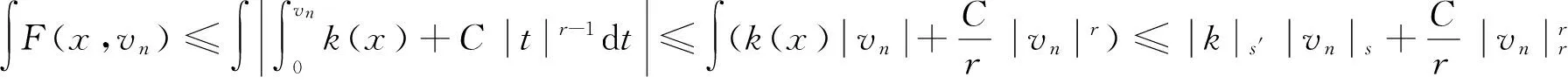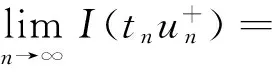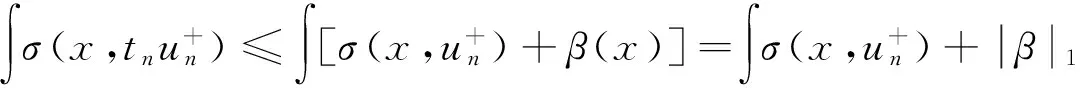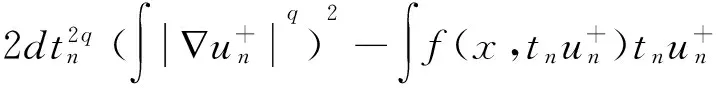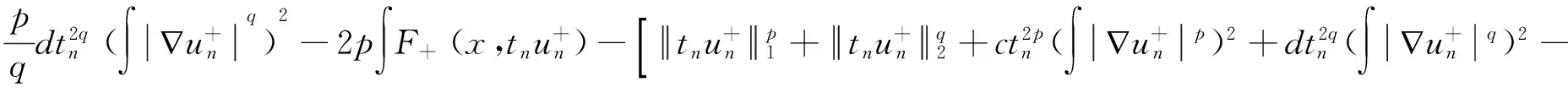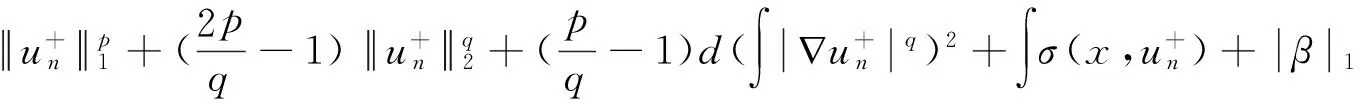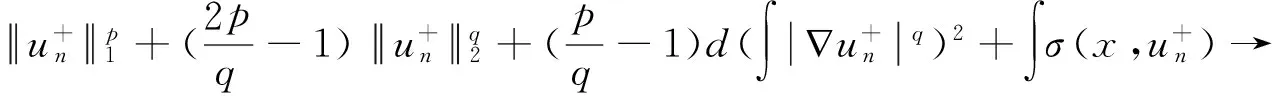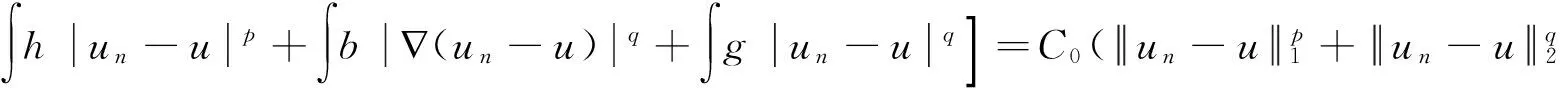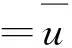一类非局部(p,q)-Laplace方程非负解的存在性
2016-06-27李瑞
李 瑞
(山西大学 数学科学学院 山西 太原 030006)
一类非局部(p,q)-Laplace方程非负解的存在性
李 瑞
(山西大学 数学科学学院 山西 太原 030006)
研究了RN中一类带有非局部项的(p,q)-Laplace方程非负解的存在性.在f(x,t)满足一定条件下,得到能量泛函Cerami序列的有界性,结合变分法证明了非负解的存在性.
(p,q)-Laplace方程; 非局部项; Cerami条件; 非负解
0 引言
考虑带有非局部项的(p,q)-Laplace方程,
(1)

(2)
当p=q>1时,方程(2)为单个p-Laplace方程.当p=q=2时,方程(2)为非线性Laplace方程
-Δu+au=f(x,u),x∈RN.
(3)
方程(2)是一般的反应扩散方程的稳定态情形,ut=div[D(u)u]+f(x,u),其中:u代表浓度;D(u)q-2,是扩散系数;f(x,u)是反应项.这类方程在物理、生物和化学中都有广泛的应用[1-4].文献[5]研究了方程(3)正解的存在性,a>0为常数.由于(p,q)-Laplace算子是非齐次的,处理一般椭圆方程的方法不再适用,文献[4,6-7]中作者运用不同的方法得到了方程(2)非平凡解的存在性.文献[4]考虑了(RN)的情形.文献[6]考虑了1 本文探究带有非局部项的(p,q)-Laplace方程非平凡解的存在性.其中f满足如下条件: (f1)f(x,t)是一个Carathéodory函数满足:f(x,0)=0,当t>0时F(x,t)>0.其中, 定理1 令2≤q 引理1Wp,a,h是自反的Banach空间,当s∈[p,p*]时,Wp,a,h→Ls(RN)为连续嵌入,当s∈[p,p*)时为紧嵌入.Wq,b,g的性质类似可得[6]. 注1 通过直接计算,并运用Hölder不等式,对任意u∈Wp,a,h,线性泛函φ∈Ep,a,hφφ)∈R是有界的,且有.定义赋范空间W=Wp,a,h∩Wq,b,g,及范数.由W的定义及引理1直接可得. 推论1W是自反的Banach空间,当s∈[q,p*]时,W→Ls(RN)为连续嵌入,当s∈[q,p*)时为紧嵌入. 序列{un}⊂W称为是C1泛函I:W→R的Cerami序列,如果满足: (C)I的任意Cerami序列在W中都有收敛子列. 用比较弱的(C)条件代替(PS)条件,定量形变引理仍成立[10].在假设(C)条件成立的情况下,山路定理也成立[11].因此,如果C1泛函I:W→R满足(C)条件及山路几何条件,则I在W中有一个临界点. 定义 引理2I+满足(C)条件. 证明 令{un}⊂W为I+的Cerami序列,则 (4) 其中K为某个不依赖于n的正常数,且 (5) (6) (7) 记 (8) 故有 (9) 由式(7)、(8)得 (10) (11) 从而可得 (12) (13) (14) 从而 由上式可得 (15) 而由式(10)可知 (16) ∫f+(x,un)(un-u)→0. (17) 对任意u∈W,由注1线性泛函φ∈W〈-Δpu,φ〉∈R,φ∈W〈-Δqu,φ〉∈R,φ∈W〈hΨpu,φ〉∈R,φ∈W〈gΨqu,φ〉∈R都有界.在W中un弱收敛于u,从而有.由算子-Δp,-Δq,hΨp,gΨq的单调性可得 hΨp(u)+gΨq(u),un-u〉, 〈-aΔpun-bΔqun+hΨp(un)+gΨq(un),un-u〉-〈-aΔpu-bΔqu+hΨp(u)+gΨq(u),un-u〉= 〈-aΔpun,un-u〉-〈-aΔpu,un-u〉+〈-bΔqun,un-u〉-〈-bΔqu,un-u〉+〈hΨp(un),un-u〉- 引理3 存在R,ρ>0使得 证明 (i) 令r∈(2p,p*).由条件(f2)、(f5),对任意ε>0,存在Cε>0使得 则 定理1的证明 由引理3,I+满足山路几何条件,结合引理2,存在0≠u∈W,对任意φ∈W满足 [1] GIOVANY M F. Existence of positive solutions for a class ofp&qelliptic problems with critical growth on RN[J]. Math Anal Appl, 2011,378(2):507-518. [2] HE C J, LI G B. The regularity of weak solutions to nonlinear scalar field elliptic equations containingp&q-Laplacians[J]. Ann Acad Sci Fenn Math, 2008,33(2):337-371. [3] LI G B, LIANG X Y. The existence of nontrivial solutions to nonlinear elliptic equation ofp-q-Laplacian type on RN[J]. Nonlinear Anal, 2009,71(5/6):2316-2334. [4] WU M, YANG Z D. A class ofp-q-Laplacian type equation with potentials eigenvalue problem in RN[J]. Bound Value Probl, 2009(1):429-436.185319. [5] LI G B, ZHOU H S. The existence of a positive solution to asymptotically linear scalar field equations[J]. Proc Roy Soc Edinburgh Sect A, 2000,130(1):81-105. [6] CHAVES M F, ERCOLE G, MIYAGAKI O H. Existence of a nontrivial solution for the (p,q)-Laplacian in RNwithout the Ambrosetti-Rabinowitz condition[J]. Nonlinear Anal, 2015,114:133-141. [7] HE C J, LI G B. The existence of a nontrivial solution to the (p,q)-Laplacian problem with nonlinearity asymptotic toup-1at infinity in RN[J]. Nonlinear Anal, 2008,68(5):1100-1119. [8] 高婷梅.含有一个参数的p-拉普拉斯方程正解的存在性[J].郑州大学学报(理学版),2014,46(3):9-12. [9] BEN-NAOUM A K, TROESTLER C, WILLEM M. Extrema problems with critical Sobolev exponents on unbounded domains[J]. Nonlinear Anal, 1996,26(4):823-833. [10] BERESTYCKI H, LIONS P L. Nonlinear scalar field equations. II. Existence of infinitely many solutions[J]. Arch Rational Mech Anal, 1983,82(4):347-375. [11] NIKOLAOS C K, NIKOLAOS S P. Nonsmooth critical point theory and nonlinear elliptic equations at resonance[J]. J Austral Math Soc Ser A, 2000,23(2):245-271. [12] DAMASCELLI L. Comparison theorems for some quasilinear degenerate elliptic operators and applications to symmetry and monotonicity results[J]. Ann Inst H Poincare Anal Non Lineaire, 1998,15(4):493-516. (责任编辑:方惠敏) Existence of Nonnegative Solution to a Class of (p,q)-Laplacian Equation LI Rui (SchoolofMathematicalSciences,ShanxiUniversity,Taiyuan030006,China) The existence of nonnegative solution to a class of (p,q)-Laplacian equation in RNwas studied. Under the assumptions off(x,t), the boundedness of the Cerami sequence of energy function was obtained. Combining variational method, the existence of the nonnegative solution was extended. (p,q)-Laplacian equation; nonlocal term; Cerami condition; nonnegative solution 2015-11-06 国家自然科学基金资助项目(11071149,11301313,11101250);山西省自然科学基金资助项目(2014021009-1, 2015021007). 李瑞(1990—), 女,山西吕梁人,硕士研究生,主要从事非线性泛函分析与非线性微分方程研究,E-mail:rli1990@sina.com. 李瑞.一类非局部(p,q)-Laplace方程非负解的存在性[J].郑州大学学报(理学版),2016,48(2):5-10. O175.2;O177 A 1671-6841(2016)02-0005-06 10.13705/j.issn.1671-6841.2015231
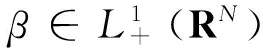
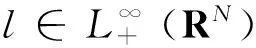

1 准备工作

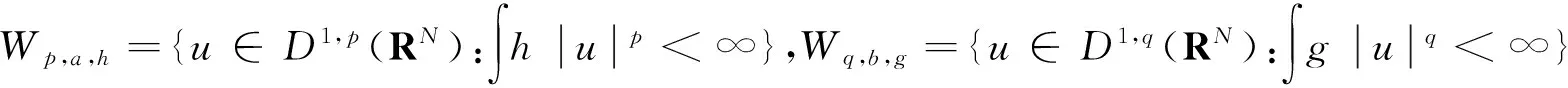



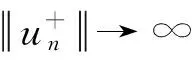
2 主要结果