石英加速度计零偏非线性集成预测
2016-06-24陈雪冬陈大志黄玉清
陈雪冬, 陈大志, 黄玉清
(1.中国工程物理研究院 电子工程研究所,四川 绵阳 621900;2.西南科技大学 信息工程学院,四川 绵阳 621000)
研究与探讨
石英加速度计零偏非线性集成预测
陈雪冬1, 陈大志2, 黄玉清2
(1.中国工程物理研究院 电子工程研究所,四川 绵阳 621900;2.西南科技大学 信息工程学院,四川 绵阳 621000)
摘要:基于小波变换(WT)的多尺度分析能力和径向基函数(RBF)神经网络良好的非线性预测与集成能力,研究了一种非线性集成预测方法。针对贮存期石英挠性加速度计零偏漂移抑制的问题,提出了基于WT和RBF神经网络的一种石英挠性加速度计零偏非线性集成预测方法。为验证所提方法的有效性,设计了一种加速度计参数的重力场标定实验,并针对某型号石英挠性加速度计进行了为期2年的标定实验。分别利用所提WT—RBF集成模型和RBF模型对零偏标定序列进行了预测分析,仿真结果显示:WT—RBF集成模型具有更好的预测性能。
关键词:小波变换; 径向基函数; 集成预测; 加速度计零偏漂移
0引言
石英挠性加速度计是高精度控制仪器,是惯性导航系统中的核心器件。在工程应用中,通过测量加速度计的输出电压,利用输入加速度与其的关系式外推出载体的运动加速度。由于外界的扰动,在贮存期间,加速度计的零偏会随着时间发生漂移,从而导致严重的导航计算误差[1]。目前常用的解决零偏漂移的方法是定期标定。因此,对加速度计零偏进行预测分析,对改良加工工艺和导航精度具有较为重要的意义。
小波变换(wavelet transform,WT)理论由于其具有多尺度分析能力,常用于非线性时间序列预测[2]。文献[3]利用WT—ARMA模型对月径流进行了预测分析,仿真结果表明,WT—ARMA模型较单一模型精度更高。文献[4]分别采用WT—ARMA模型和WT—BP模型对网络流量进行了预测分析,对比发现WT—BP模型的预测精度和模型复杂度都要优于WT—ARMA。而径向基函数(radial basis function,RBF)神经网络的预测能力和泛化能力均优于BP神经网络,且较BP神经网络具有迭代次数少,收敛速度快和网络结构简单等显著优势[5],且可非线性集成多个模型的预测结果,具有较好的预测性能[6]。
本文以此为出发点,研究了一种加速度计零偏序列的非线性集成预测方法,通过Mallat快速WT算法,分离出零偏序列中的趋势信号和细节信号,运用RBF网络对各信号序列进行预测,最后利用RBF网络集成各序列的预测结果得到零偏的预测值。为了验证所提方法的有效性,针对中国工程物理研究院生产的某型号加速度计零偏标定实验数据分别应用WT—RBF集成模型和RBF模型进行了预测仿真,计算结果表明:WT—RBF集成模型的预测精度较单一模型更高。
1非线性集成预测模型
1.1WT
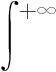
(1)
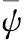
离散WT由Mallat快速算法[7]实现,Mallat算法是运用高通滤波器和低通滤波器对原始信号进行抽取和重构的过程。设第i分解层的低频分量为Ci、高频分量为Dj,正交小波滤波器分别为H(低通)、G(高通),则该尺度的Mallat算法的分解与合成的表达式为
(2)
Ci-1(n)=∑H(k-2n)Ci(n)+
∑G(k-2n)Di(n)
(3)
1.2RBF模型
RBF网络是一种三层的前馈式神经网络。它具有结构简单、收敛快、局部逼近能力强等优点,是一种非线性能力非常优异的人工智能预测模型。它的训练过程通常分为两个阶段[8]:1)利用输入向量计算隐含层各神经元的计函数中心cj和基函数宽度σ;2)由最小二乘法求得输出层的权值w。实际使用Matlab仿真过程中,函数中心cj、宽度σ和权值w交由程序进行计算,通过不断调整隐含层神经元个数,优化三个参数的值,以得到最优的参数。
1.3非线性集成模型原理
基于小波分析与RBF模型的优点,所研究的WT—RBF集成预测模型如图1所示。
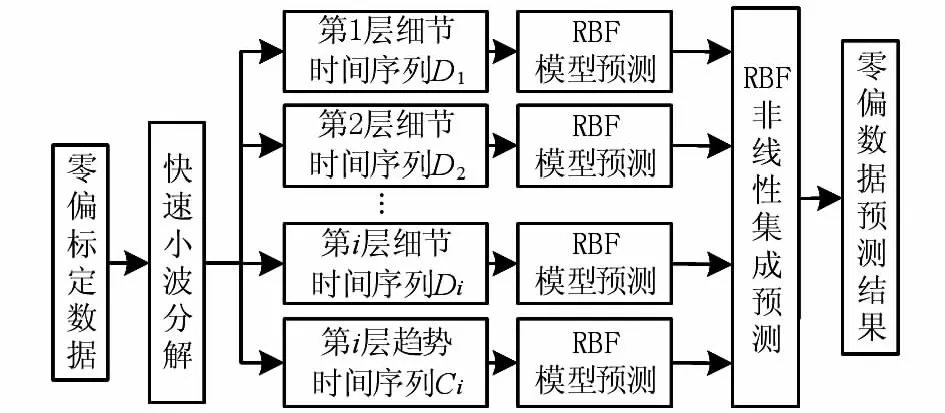
图1 WT—RBF网络预测模型Fig 1 WT—RBF integrate prediction model
WT—RBF集成模型的计算过程:
1)确定小波基函数与分解层数,利用Mallat算法对零偏数据进行分解为一个平滑低频信号Ci和多个高频信号D1,D2,…,Di(i为小波分解层数)。
2)对分解后的每个序列进行RBF预测建模。首先归一化处理,确定RBF神经网络的输入节点大小m,并按照式(4)将一维时间序列转换成一个多维时间序列。将训练序列划分为学习序列和检验序列,通过不同值的尝试训练得到使检验序列预测精度最佳的goal和S,利用所得最优参数对原训练序列进行训练、预测并作反归一化处理,得到各序列的拟合值与预测值
(4)
3)最后,对各序列的预测值进行RBF非线性集成得到零偏预测值。集成模型输入层数为i+1,利用各模型的拟合值进行模型训练,再利用训练好的集成模型和各序列的预测值进行集成处理,得到零偏预测值。
2加速度计零偏实验仿真
2.1数据来源与评价指标
本文选择重力翻转实验来进行加速度计的参数标定。标定实验环境设置为温度25 ℃,湿度40 %RH。数据采集系统[9]如图2所示,石英挠性加速度计被安装在特种钢材制成的六面体中,下方为有90°凹陷的卡槽底座,每次标定以0°为起点,每个角度测试5 min,并进行滤波处理[10],采集完成后翻转45°,继续采集,共采集翻转一周8个角度下的加速度计输出电压E。标定实验为期2年,标定周期为4天,实验对象为一组18个不同工艺制作的石英加速度计。
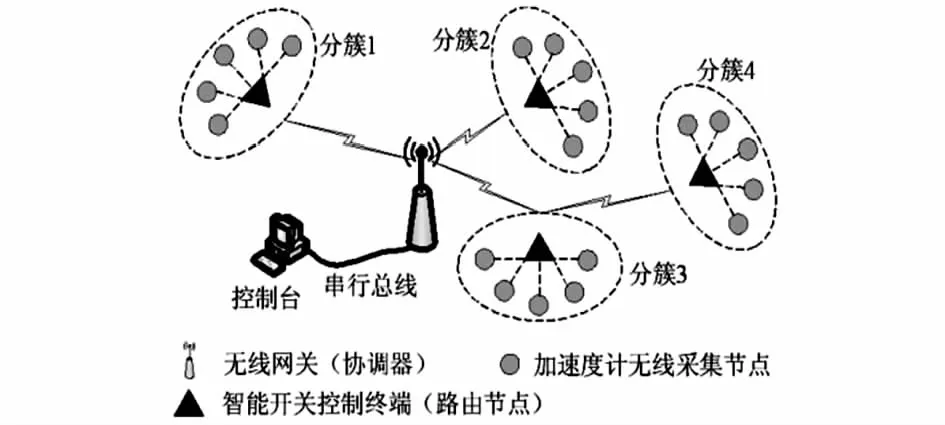
图2 加速度计数据采集系统Fig 2 Data acquisition system of accelerometer
加速度计呈“摆状态”安装,可知加速度计输入轴的输入加速度为ai=gsinθ,θ为加速度计翻转角度,g为当地重力加速度。标定模型选用加速度计二阶模型,取模型公式为
(5)
式中K0为零偏值;K1为标度因数;K2为二阶非线性系数;aout为加速度计输出加速度值。
利用总体最小二乘法和公式(5)对实验数据进行参数辨识得到零偏标定值K0。取标号为V146的加速度计的零偏标定数据为研究对象,如图3所示,设其零偏标定序列为{Xt},将标定序列{Xt}按照8∶1∶1比例划分学习序列、检验序列和验证序列。
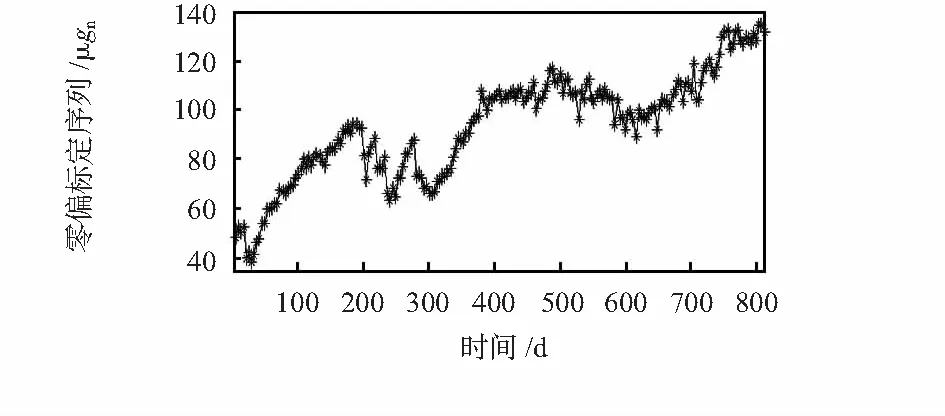
图3 加速度计零偏标定序列Fig 3 Zero-bias calibration sequence of accelerometer
选择预测评价中常用的均方根误差(root means square error,RMSE)作为准则来评价预测性能,其公式分别为
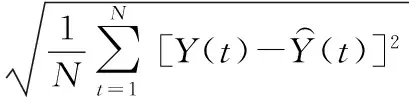
(6)
式中Y⌒(t)为预测值;Y(t)为真实值;N为样本数。
2.2零偏预测建模
本文以Matlab数据分析软件为平台,对零偏标定序列{Xt}进行仿真分析。
首先,对零偏序列{Xt}进行WT。小波基函数选择db4小波,它是紧支撑标准正交小波。经实验分析发现,分解层数为3时,预测精度最高,分解层数继续增大对预测精度的提升效果不显著。零偏序列的分解得到的趋势序列C3、细节序列D1~D3,如图4所示。
其次,利用RBF神经网络对各序列进行拟合预测,得到各验证序列的预测值C⌒3,D⌒3,D⌒2,D⌒1。
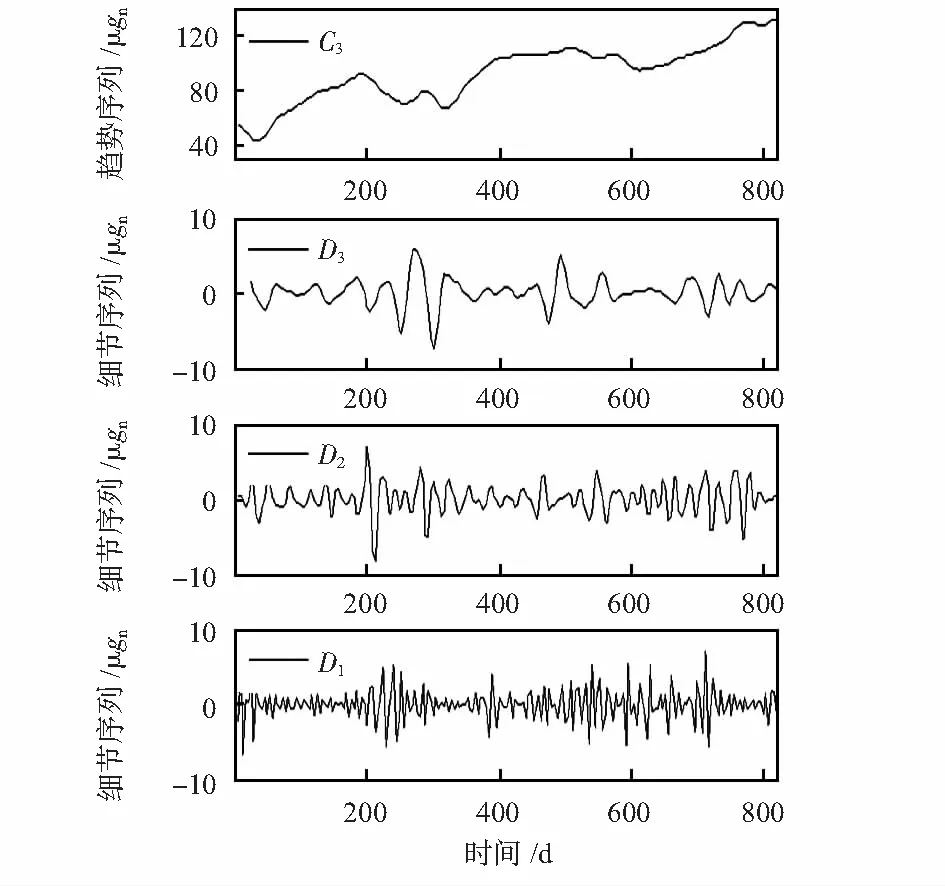
图4 零偏序列的小波变换结果Fig 4 Results of WT of zero-bias sequence
最后,进行RBF神经网络非线性集成训练。集成模型结构为4×4×1,目标的RMSE为3×10-6gn,扩展因子为20。将各序列的预测值C⌒3,D⌒3,D⌒2和D⌒1输入集成模型,得到零偏验证序列的预测值Y⌒(t)如图5所示。
从图5(a)中可以看到,采用RBF和WT—RBF集成模型的预测曲线都非常接近实际的标定值,较好地预测了零偏漂移的趋势,WT—RBF集成模型与真实值的契合度更好,证明了所研究的预测方法的有效性。从图5(b)中可以看到,WT—RBF集成模型的预测残差范围为-2.44~5.34 μgn,而单一RBF模型的预测残差范围为-6.35~11.71 μgn,显然WT—RBF集成模型预测残差更小。
利用公式(6)可以得到WT—RBF集成模型的RMSE为2.27 μgn,而RBF模型的RMSE为4.91 μgn。WT—RBF模型的预测精度更高。
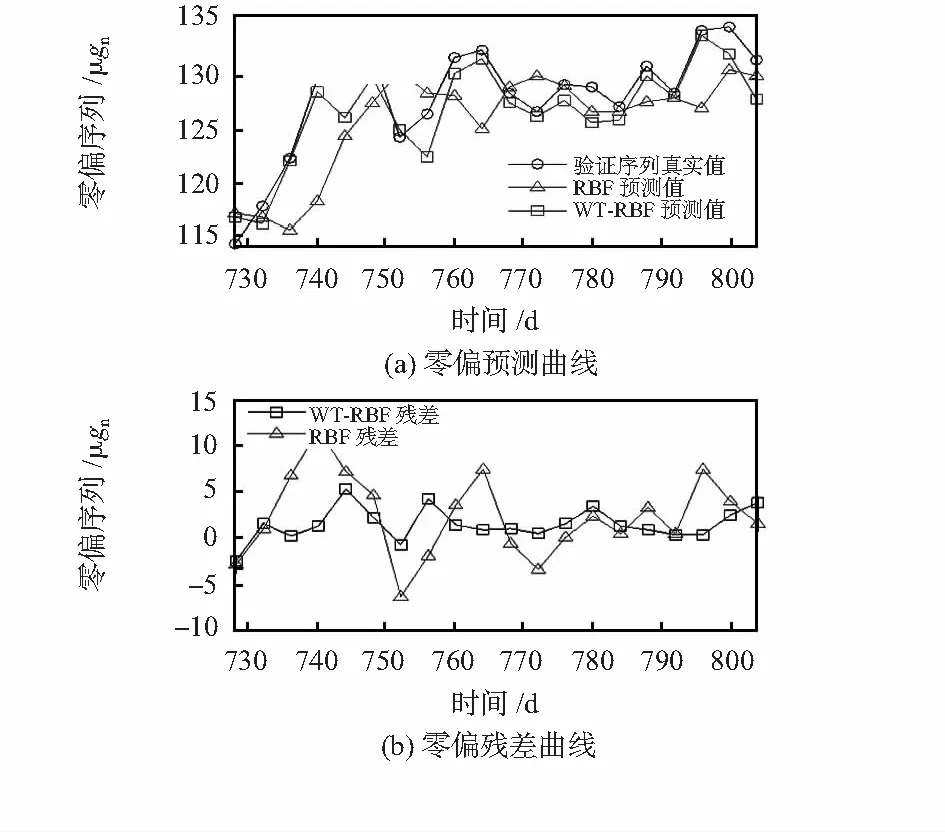
图5 加速度计零偏预测结果Fig 5 Prediction result of accelerometer zero-bias
3结论
本文针对自然贮存条件下石英加速度计零偏参数漂移的抑制问题,根据零偏变化的特点,研究了一种WT—RBF非线性集成预测方法。仿真结果表明:WT—RBF模型对比单一RBF模型具有更高的预测精度。因为影响石英加速度计参数变化的有胶粘剂性能老化、硬磁材料失磁以及残余应力的释放等多种因素,单独使用RBF网络对零偏进行预测时,拟合曲线较平滑,丢失较多细节信息。而WT—RBF集成模型利用小波分解的多尺度分析能力,将对不同分辨率下的序列分别进行拟合预测,较好地提取了原序列的细节,又利用RBF的非线性集成能力,避免了多个预测值叠加导致的误差扩大,保证了预测精度,具有更好的预测性能。
参考文献:
[1]王洪,李磊民,黄玉清.石英挠性加速度计零偏分析与建模方法[J].自动化仪表,2014,35(11):13-19.
[2]刘向丽,王旭朋.基于小波分析的股指期货高频预测研究[J].系统工程理论与实践,2015,35(6):1425-1432.
[3]周惠成,彭勇.基于小波分解的月径流预测校正模型研究[J].系统仿真学报,2007,19(5):1104-1108.
[4]黎志勇,李宁.基于小波的非平稳时间序列预测方法研究[J].计算机工程与应用,2014,50(10):38-43.
[5]陈烈,张永明,齐维贵,等.基于RBF神经网络的时间序列交叉供热负荷预报研究[J].电子学报,2009,37(11):2444-2447.
[6]冯雪,张金锁,邹绍辉.基于RBF神经网络非线性集成模型的天然气需求预测[J].统计与决策,2015,31(11):91-93.
[7]Stéphane G Mallat.A theory for multi resolution signal decomposition:The wavelet representation[J].IEEE Trans on Pattern Anal Mach Int,1989,11(7):674-693.
[8]Powell M J D.Radial basis functions for multivariable interpolation:A review[C]∥IMA Conference on Algorithms for the Approximation of Functions and Data,Shrivenham:Royal Military College of Science,1985.
[9]陈雪冬,张德.石英挠性加速度计网络化自主测试系统[J].传感器与微系统,2014,33(8):65-68.
[10] 陈雪冬,陈硕红,徐伟.加速度计信号的小波形态滤波与样本熵分析[J].自动化仪表,2014,35(5):22-25.
Nonlinear integrate prediction of quartz accelerometer zero-bias
CHEN Xue-dong1, CHEN Da-zhi2, HUANG Yu-qing2
(1.Institute of Electronic Engineering,China Academy of Engineering Physics,Mianyang 621900,China;2.School of Information Engineering,Southwest University of Science and Technology,Mianyang 621000,China)
Abstract:Based on multi-scale analysis capabilities of wavelet transform and good nonlinear prediction and integrated capabilities of RBF neural network,a nonlinear integrate prediction method is studied.Aiming at problem of zero-bias drift inhibition during storage,of quartz elastic accelerometer,a zero-bias nonlinear integeration predictive method for accelerometer,which based on WT and RBF,is proposed.In order to verify the effectiveness of the proposed method,a gravitational field calibration test of accelerometer parameters is designed.The two-year calibration experiment of some type quartz accelerometer is carried out.Prediction analysis on zero-bias calibration sequence by WT—RBF integrate model and RBF model,simulation results show that the WT—RBF integrate model,compared with the single RBF model,has better prediction performance.
Key words:wavelet transform(WT); radial basis function(RBF); integrate prediction; accelerometer zero-bias drift
DOI:10.13873/J.1000—9787(2016)04—0011—04
收稿日期:2015—10—09
中图分类号:TP 391
文献标识码:A
文章编号:1000—9787(2016)04—0011—04
作者简介:
陈雪东(1967-),男,湖南邵阳人,副研究员,主要研究领域为传感器测试与信号分析处理。
