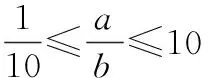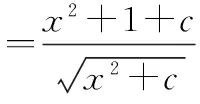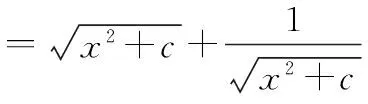优化解题过程 培养思维能力

龙正祥

(陕西省西安惠安中学，710302)

优化解题过程培养思维能力

龙正祥

(陕西省西安惠安中学，710302)

数学教育作为培养人的思维能力、创新意识,是丰富多彩、充满活力的．新课程标准强调:高中数学课程应注重提高学生的数学思维能力,这是数学教育的基本目标之一．从高考改革的趋势来看,将来的高考试题会给思维能力强的学生留下了充分施展才能的空间，在高考中这种思维能力主要体现在解题能力上.解题能力的提高在高考数学复习课中,主要是让学生通过一题多法、多题共法、一题多变、一题多用、一题多联的思维训练逐渐培养思维灵活性、广阔性、严谨性、批判性、深刻性等品质．

一、一题多法，培养思维的灵活性

解法1(利用三角函数的有界性) 设动点D(3+cosθ,sinθ),则

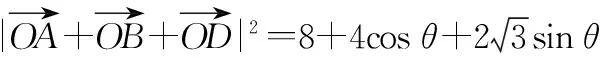
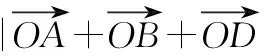
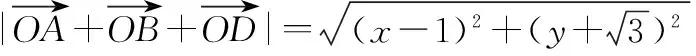
解法3(利用三角不等式)

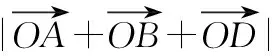
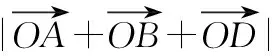
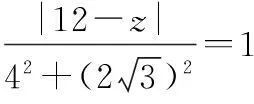
由柯西不等式，得

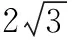
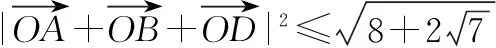
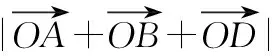
需要特别指出的是,一题多法的价值并不是为了使学生掌握这道题的所有解法,而在于使学生学会从不同角度、不同方位去审视、去思考,从而沟通知识之间的纵横联系,激发学生的求知欲,达到培养学生思维灵活性品质的目标.要实现这一目标,需教师引导学生多方位思考,并及时调整，否则可能造成学生的迷惘,走入误区.

二、多题共法，培养思维的广阔性

例2(1)设关于x的方程x2+2x+a=0在(0,+∞)上有解,求实数a的取值范围.

(2)设关于x的方程sin2x+2sinx+a=0有解,求实数a的取值范围；

(3)设关于x的不等式sin2x+2sinx+a>0有解,求实数a的取值范围.

(4)设关于x的不式sin2x+2sinx+a>0恒成立,求实数a的取值范围.

经过分析、比对,虽然这个例子中(1)～(4)数学情境不同,分别以二次方程、三角方程、三角不等式的“面孔”出现,但其本质特征——通过两个变量的相互关系,寻找其中一个变量的取值(范围)是相同的,所以都可以用“分离法”解决.

对第(4)问略解如下:

sin2x+2sinx+a>0恒成立等价于a>-(sinx+1)2+1对x∈R恒成立.

∵f(x)=-(sinx+1)2+1的最大值为1,故所求a的取值范围是(1,+∞).

多题共法需要学生有一定的类比、观察和概括能力,对学生掌握基本数学技能和解题规律性有着一定的积极作用,能达到做一题,会一类;用一法,解多题的效果.有利于求同思维的发展,有利于培养学生思维的广阔性.

三、一题多变——培养思维的严谨性

例3已知a,b,c,d∈R,且a2+b2=1,c2+d2=1,求证:|ac+bd|≤1.

在学生用比较法、分析法、综合法证明之后, 可启发学生反思是否还有其它解法.经过学生独立思考、合作交流,分析归纳出柯西不等式法、三角代换法、向量法、复数法、几何法等方法.通过师生共同探究,还可以将例题变形、推广,得出一系列新题:

变式2已知a,b,c,d∈R,且a2+b2=1,c2+d2=1,求证:|ac-bd|≤1；

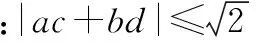
变式5已知a,b,c,d∈R,且a2+b2=1,c2+d2=1,ab+cd=1,求证:ab-cd=0；

以“原型题”作为素材,适当改变条件或问题背景；或对问题作横、纵向拓展引申,能大大增强学生对问题的认识,辩证地分析和应用条件,对培养思维严谨性大有裨益.课堂教学中若能发挥此类题的辐射作用,可起到事半功倍的效能.

四、一题多用，培养思维的批判性

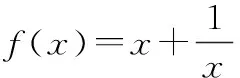
该题的证明比较简单，这里从略.此函数不妨简称“对勾”函数,其单调性在求最值方面用途非常广泛,我们可以利用这种函数的结论或方法解决一类函数最值问题.

(i)若0

(ii)若c>1,求f(x)的最小值.

f(t)min=f(1)=2.

由单调性可得

利用基本不等式求最值是常用方法之一,但取“=”条件不具备时,我们应想到利用“对勾”函数的单调性,让例4的功用得到彰显.

五、一题多联——培养思维的深刻性

思路1鉴于MF1和MF2是椭圆上点与两焦点连线,故可联系椭圆定义.

∵|MF1|+|MF2|=2a,

|MF1|2+|MF2|2=4c2,

思路2由F1M⊥F2M,可联系直线的斜率.设M(x0,y0) (-a

①

又点M在椭圆C上,有

②

思路3采用“交轨法”,联系点M上是以F1F2为直径的圆上.

因为F1M⊥F2M,所以点M所在的轨迹方程为x2+y2=c2.

与椭圆方程联立,可得

(a2-b2)x2-a2(c2-b2)=0,

思路4由F1M⊥F2M及张角∠F1MF2大小随点M的变化趋势,可联系运动观念.

一个数学问题,可从不同角度、不同的知识点出发,都能得到圆满的解决.同时，在问题解决过程中,思维的广阔性、深刻性也得到深化．