从教材练习题到高考压轴题——例谈“求递推数列通项公式”的教学

江创树

(广东省揭阳市揭东区第二中学，522000)

从教材练习题到高考压轴题
——例谈“求递推数列通项公式”的教学

江创树

(广东省揭阳市揭东区第二中学，522000)

递推数列是高考数列压轴题的主要类型之一,特别是近几年的广东高考,对递推数列的考查更是情有独钟.这类问题是一类比较难以处理的问题,学生碰到这类问题往往手足无措,无从下手.高考中这类问题的得分率很低，这是教学中的一个难点问题．

笔者在教学中发现,老师如果能从教材出发,科学合理地利用教材,注重对教材中的通识、通法以及例题、习题进行变形引申,引导学生用变化发展的眼光观察这些例题、习题,归纳出解决问题的系统方法,扎实打好基础,学生在高考中碰到这些难题便能做到心中有数,这些难题也会迎刃而解．本文就教材中的一道习题及其变式练习与一道高考压轴题的联系,谈谈笔者在求递推数列通项公式的教学中的一些做法．

例1已知数列{an}中,a1=5,a2=2,an=2an-1+3an-2(n≥3)．对这个数列的通项公式作一研究,能否写出它的通项公式?

解由题意，可设

an+λan-1=μ(an-1+λan-2)，

则an=(μ-λ)an-1+μλan-2.

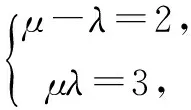
由an=2n-1+3an-2,得

an-3an-1=-(an-1-3an-2)，

或an+an-1=3(an-1+an-2).

又∵a1=5,a2=2，

∴{an-3an-1}是以a2-3a1=-13为首项,-1为公比的等比数列;{an+an-1}是以a2+a1=7为首项,3为公比的等比数列．

由等比数列的性质，可得

an-3an-1=-13·(-1)n-2,

即an-3an-1=13·(-1)n-1，

①

又an+an-1=7·3n-2.

②

由① 、② ，可解得

评注这是新课标人教A版必修5第二章复习参考题B组的一道练习题,其原型是an=pan-1+qan-2(其中p、q为常数).这类问题有多种不同的解法,如数学归纳法、构造法、特征根法等．上述解答过程用到了构造法,在教学中可以引导学生对该问题进行变形引申得到如下题目，从而引导学生归纳总结出形如an=pan-1+qan-2(其中p、q为常数)这类题目的一般解法．

例2已知数列{an}中,a1=1,a2=4,an=4an-1-4an-2(n≥3)，求该数列的通项公式．

解由题意，可设

an+λan-1=μ(an-1+λan-2)，

则an=(μ-λ)an-1+μλan-2.

对比an=4an-1-4an-2，可得

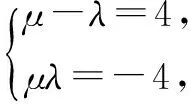
由an=4an-1-4an-2，得

an-2an-1=2(an-1-2an-2),

又a1=1,a2=4,

∴数列{an-2an-1}是以a2-2a1=2为首项,2为公比的等比数列．

由等比数列的性质,可得

an-2an-1=2·2n-2，

即an-2an-1=2n-1，

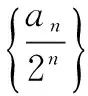
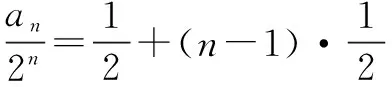
∴an=n·2n-1．

评注在讲解教材中的例题之后,对例题进行变形,引导学生解答变形后的题目,最后归纳总结出如何利用构造法求形如an=pan-1+qan-2(其中p、q为常数)递推关系的数列的通项公式．解答过程中,我们构造出新的递推关系an+λan-1=μ(an-1+λan-2),再根据其与题设给出的递推关系求参数λ、μ.当λ、μ有两组解时,我们可以利用解方程组的思想求出{an}的通项公式(如例1)；当λ、μ只有一组解时,我们可再次利用构造法求出{an}的通项公式(如例2)．通过对比我们可以比较直观地让学生对如何求形如an=pan-1+qan-2(其中p、q为常数)递推关系的数列的通项公式有较为全面的认识．由此可见,在平时的教学中,如果教师能经常引导学生用发展变化的眼光去观察教材中的例题、练习，熟练地掌握教材介绍的通识、通法，在高考中,我们对这类问题便能以不变应万变,处变不惊．接下来我们再来看一道经典的高考压轴题．

例3(2008年广东高考题)设p，q为实数,α，β是方程x2-px+q=0的两根,数列{xn}满足x1=p,x2=p2-q,xn=pxn-1-qxn-2(n=3、4、5…)．

(1)证明:α+β=p,αβ=q；

(2)求数列{xn}的通项公式；

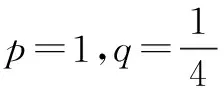
解(1)略．

(2)由题意，设

xn+λxn-1=μ(xn-1+λxn-2)，

则xn=(μ-λ)xn-1+μλxn-2.

又xn=pxn-1-qxn-2，

又由(1)知α+β=p,αβ=q，可解得

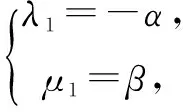
故由xn=pxn-1-qxn-2，可得

xn-αxn-1=β(xn-1-αxn-2)，

或xn-βxn-1=α(xn-1-βxn-2)，

∴数列{xn-αxn-1}、{xn-βxn-1}分别是以β、α为公比的等比数列．

由等比数列的性质，可得

xn-αxn-1=(x2-αx1)βn-2，

③

xn-βxn-1=(x2-βx1)αn-2.

④

∴(i)当α≠β时,由③ 、④， 可得

(β-α)xn=(x2-αx1)βn-1-(x2-βx1)αn-1.

又x1=p,x2=p2-q,α+β=p,αβ=q,

∴(x2-αx1)βn-1=βn+1,

(x2-βx1)αn-1=αn+1，

∴(β-α)xn=βn+1-αn+1，

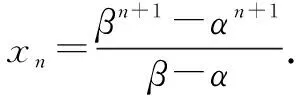
(ii)当α=β,即Δ=p2-4q=0时,

λ=-α=-β,μ=α=β.

由③ 或④ 及x1=p,x2=p2-q,α+β=p,αβ=q，可得

xn-αxn-1=αn,

∴xn=(n+1)αn.

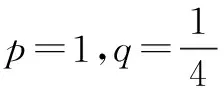
评注这是2008年广东高考卷的压轴题,其主要难点在第(2)小题,利用递推关系求数列的通项公式.由上面的解答过程我们不难看出,此题考查的内容只是将我们前面两道例题综合起来,并将其一般化而已．如果我们在平时的教学中,能引导学生对前面两个例题进行归纳总结,学生们在高考中就能心中有数．所以,只要我们在平时的教学中不断引导学生用发展变化的眼光去对待教材中的习题,并及时地进行归纳整理,做到对教材有整体的认识,高考时便能得心应手地化解难题，立于不败之地．

递推数列存在较多的类型,各种类型的特点不尽相同.为了较为更好地阐述如何利用教材对求其通项公式的方法进行教学,我们再看看在平时的教学中,如何利用教材求下面这几种类型递推数列的通项公式．

类型1an=an-1+f(n);

类型2an=f(n)an-1;

类型3an=pan-1+q(p、q为常数).

综上所述,求递推数列的通项公式既是教学的难点,又是高考的重点,近几年的高考经常考查,学生的得分率比较低．通过我们上面的分析,只要老师们在教学中合理科学地利用教材,科学地对教材中的例题、习题进行变式引申,引导学生用发展变化的眼光对待教材中的例题、习题,引导学生熟练掌握通识、通法,及时地进行归纳总结，在高考中碰到这样的问题便能胸有成竹，顺利求解．