浅析高中数学试题中的“陷阱”
2016-06-24刘学亮
刘学亮
(江苏省徐州市铜山区棠张中学,221113)
浅析高中数学试题中的“陷阱”
刘学亮
(江苏省徐州市铜山区棠张中学,221113)
在高中数学命题过程中,命题者为了考查学生的基础知识、基本技能,往往更喜欢设置学生注意不到的“陷阱”.如果学生基础知识掌握得不扎实,且在做题时对命题者设计的“陷阱”视而不见,那么就会严重失分.我们只有清楚命题者在哪些方面设置“陷阱”,才可能绕过“陷阱”顺利解题,从而达到事半功倍的效果.
一、针对学生对概念掌握不清设置“陷阱”
命题人往往围绕数学概念设置“陷阱”.如果相关的定理、定义、公式掌握不清,理解有偏差,就会就会掉入“陷阱”之中.因此吃透每一个概念,理解其真正的含义才能绕过“陷阱”顺利解题.
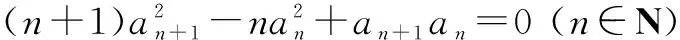
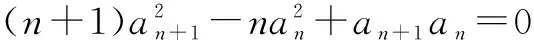
(an+1+an)[(n+1)an+1-nan]=0.
而{an}是正项数列,即an+1+an>0,
从而(n+1)an+1-nan=0,
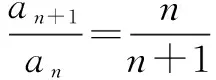
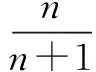
二、针对思维的片面性设置“陷阱”
解题时如对题目分析片面,就会陷入困境之中,只有全面地分析题目才能从“陷阱”中走出来,才能真正地把握解题思路,从而达到正确解题的目的.
例2已知数列{an}为等差数列,公差d≠0,其中ak1,ak2,ak3,…,akn恰为等比数列,若k1=1,k2=5,k3=17,求k1+k2+k3+…+kn.
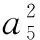
(a1+4d)2=a1(a1+16d)(d≠0),
解得a1=2d.
因此该数列的前三项为2d,6d,18d,公比为3,所以
akn=2d·3kn-1.
又因为akn=a1+(kn-1)d=(kn+1)d,
所以2d·3kn-1=(kn+1)d,
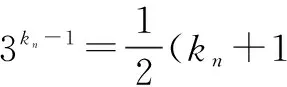
剖析以上解答中akn为等差数列的第kn项,但在等比数列ak1,ak2,ak3,…,akn中为第n项,得akn=2d·3kn-1是错误的.上述错误主要错在对题目给出的条件分析不全面造成的.
三、针对思维定势设置“陷阱”
命题人往往根据人们习惯于用固定的思维模式或方法分析问题,盲目套用一些公式或结论等特点设置“陷阱”,若我们不仔细观察,稍微不慎就会滑入“陷阱”.
例3设四个数成等比数列其乘积为16,中间两项的和为5,试求公比q的值.
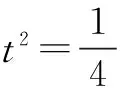
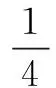
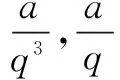
四、针对隐含条件,设置“陷阱”
隐含条件往往是很难发现的,可透过现象看本质,发现的愈多揭露问题的本质愈深.有些题目的题设条件并不那么明显,有明有暗,如不认真考虑斟酌挖掘隐含条件,就会掉入“陷阱”.
例4已知3sin2α+2sin2β=2sinα,求S=sin2α+sin2β的最大值和最小值.
错解由3sin2α+2sin2β=2sinα,得
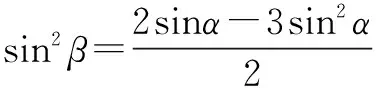
代入S=sin2α+sin2β,得
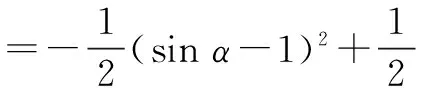
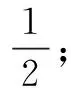
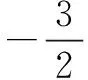
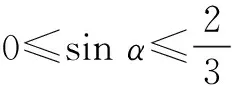
五、针对学生缺乏知识的应用能力,设置“陷阱”
学生在平时的学习中,主要是机械地去接受知识,很少注意知识应用能力的培养.当学生遇到实际问题时,就不会运用相应的知识解决问题,就会很容易掉入命题者设置的“陷阱”.
例5某同学把一枚硬币抛掷100次,出现50次反面的可能性很大吗?
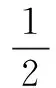
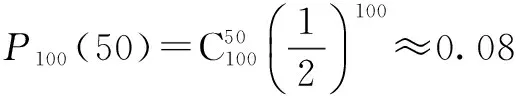
说明这个事件发生的概率很小.
六、针对学生解题的粗心大意,审题不细设置“陷阱”
有些题目的题设条件对解题的方法有限制,如果审题不细,粗心大意,注意不到一些条件,就会掉入命题者设置的“陷阱”.
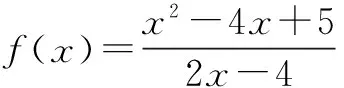
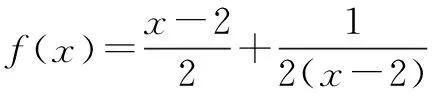
因为x≥4,故x-2≥2,
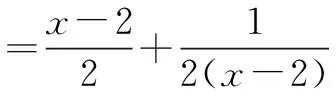
=1.
七、针对学生画函数图象忽略极限的思想设置“陷阱”
学生在画函数图象时容易忽略极限的思想,最终图象画得不准确,导致题目解答不对,最终掉入命题者设计的陷阱.
例7已知y=ax-lnx有两个零点,求a的取值范围.
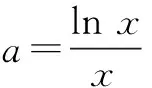
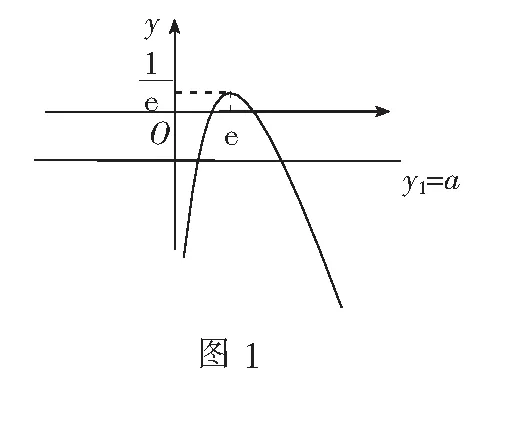
总之,当我们能了解到高中数学命题中的陷阱,在做题时可以跳过陷阱,达到有效解题的目的.
