新融合小波变换与低秩矩阵恢复图像去噪算法
2016-06-24吴君钦
吴君钦,邬 亮
(江西理工大学 信息工程学院,江西 赣州 341000)
新融合小波变换与低秩矩阵恢复图像去噪算法
吴君钦1,邬亮2
(江西理工大学信息工程学院,江西赣州341000)
摘要:针对小波阈值图像去噪会引入量化噪声和阈值选取不当会损失图像本身有用信息的问题,提出一种新的融合小波变换与低秩矩阵恢复(Low Rank Matrtix Recovery,LRMR)的图像去噪算法。不同于传统的单一阈值的去噪算法,所提出的算法在单一阈值上结合了低秩矩阵恢复算法,这样不仅能进一步消除噪声,同时还能修复被噪声损坏的数据,而且更能适应各种不同的噪声环境。首先,选取固定阈值对图像矩阵进行小波去噪处理。其次,采用增广拉格朗日乘子算法最小化矩阵核范数。最后,将矩阵分解为低秩逼近矩阵和稀疏误差矩阵。实验结果表明,算法获得了较高的峰值信噪比,在不同噪声环境下有较高的鲁棒性。
关键词:小波变换;图像去噪;增广拉格朗日乘子;低秩矩阵恢复;最小核范数
1图像去噪
图像去噪是图像处理中一个重要的环节,传统的图像去噪方法分为空域去噪[1]和频域去噪[2]。在目前大部分的研究中无论是空域去噪还是频域去噪采用的方法都比较单一。
相对于传统的去噪方法,小波去噪[3-5]具有多分率的特点。目前大部分的研究基于小波阈值去噪的改进主要集中在去噪阈值的选取上面。文献[4]选用了一种新的平滑的阈值函数代替传统阈值函数。文献[5]在多个不同尺度上选用不同阈值函数去噪。但是这种基于阈值改进的去噪算法在进行小波系数量化时不可避免地会引入量化噪声,并且阈值选取不当,去噪效果不太理想,还可能损害图像本身的有效数据信息,而且也没有去除低频部分噪声。
为了解决小波基于阈值的方法会引入量化噪声和去噪过程未考虑低频噪声,阈值选取不当会损害图像有用信息的这两个问题,本文在小波去噪的基础上,结合低秩矩阵的最小核范数约束来解决这两个问题。低秩矩阵最小核范数约束进行图像去噪时,直接将整个图像矩阵作为整体处理,可以消除小波阈值去噪过程引入的量化的噪声和小波阈值去噪未考虑的低频部分噪声,同时还能修复在小波去噪过程中受损的矩阵信息。将低秩矩阵最小核范数约束和小波变换结合能够使算法能适应不同的噪声环境,增强了算法的鲁棒性,扩充了算法的适用范围。
2传统的小波阈值去噪简介
小波去噪根据所给出的阈值重构小波系数矩阵,小波去噪中常用的阈值为
(1)
式中:δ为噪声方差;N为信号长度。
对小波高频系数w(i,j)重构的硬阈值方法为
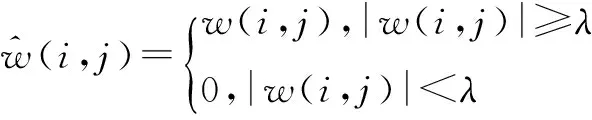
(2)
软阈值方法为
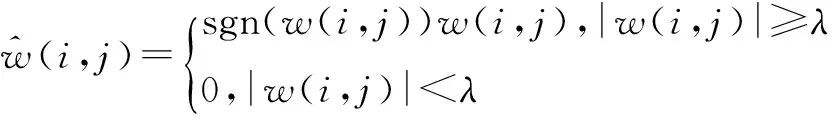
(3)
文献[4]改进阈值算法为
(4)
图像矩阵经过小波变换后,得到小波系数矩阵,然后根据式(2)、(3)、(4)重构小波系数矩阵,最后通过小波逆变换得到去噪后的图像矩阵。传统的基于小波阈值的去噪算法只是简单地将一些高频高频系数置0,没考虑低频噪声部分,并且根据单一阈值直接置0系数可能会损坏图像本身有用信息,因此本文在单一阈值基础上引入低秩矩阵最小核范数优化来解决这些问题。
3融合小波变换与低秩矩阵恢复的图像去噪算法
3.1算法思想
传统小波阈值算法和文献[4]改进算法中,直接将小于阈值的高频部分小波系数量化为0,这会引入量化噪声。小波高频系数不仅有噪声系数还包含了图像的边缘信息。根据式(1),如果噪声较大,在数据长度不变的情况下,噪声方差δ大,阈值λ较大,根据式(2)、(3)、(4)将较多的高频系数置0,因而会错误地将图像的边缘的小波系数置0,破坏了图像本身的有用信息。并且,基于阈值的算法仅考虑了高频系数的噪声,实际大多数噪声在低频系数部分也有分布。由于小波低频系数包含了较多的图像细节信息,直接用阈值法处理低频部分的小波系数将会损害图像本身的细节信息,不仅达不到去噪目的反而会使得图像质量更差。低秩矩阵恢复算法对噪声的去除是直接在原始图像上进行,因而能克服小波对于频域去噪的不足。并且,由于低秩矩阵恢复算法还有修复数据的能力,能够修复被噪声污染的数据,使得最后结果更加鲁棒。
应用低秩矩阵恢复算法时,要求数据矩阵具有低秩特性和误差矩阵的稀疏特性。直接在原始图像矩阵处理时,由于实际噪声分布可能不满足稀疏特性造成低秩矩阵恢复算法性能的下降。经过小波去噪处理后,大部分噪声去除,噪声分布更能满足噪声误差矩阵的稀疏性要求,使得本文算法更加鲁棒。
3.2低秩矩阵恢复算法
根据数学理论,矩阵D是由低秩矩阵A受到噪声E的破坏形成的,并且E是一个稀疏矩阵[6],即E中只有少量的非零元素。因此可以用LRMR来进行问题求解,LRMR可用式(5)优化问题来表示

(5)
s.t.D=A+E
式(5)理论可行,实际上是一个NP问题。根据现有理论,矩阵0范数可用矩阵1范数近似替代。矩阵rank函数,可用矩阵核范数近似替代。因而,式(5)优化问题就可用式(6)优化问题近似代替
(6)
s.t.D=A+E
求解式(6)的优化问题有多种优化算法,常用的算法有迭代阈值法[7]、加速近端梯度法[8]、对偶法[9]与增广拉格朗日算法[11](AugmentedLagrangemultipliers,ALM)。
本文算法涉及的几个概念解释如下:
定义1,矩阵的范数。矩阵A=(aij)∈Rm×n的Frobenius范数为

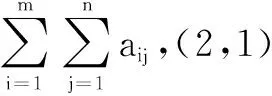
定义2,矩阵内积。同型矩阵A,B的内积为
(8)
矩阵X的奇异值分解为
(9)
式中:U∈Rm×m和V∈Rn×n均为正交矩阵。对角矩阵Σr=diag(δ1,δ2,…,δr)∈Rr×r,且对角元素满足δ1≥δ2≥…≥δr。奇异值阈值算子为
Dτ(X)=U∑rVT
(10)

低秩矩阵恢复问题实际是矩阵的核范数最小化的优化问题,矩阵最小核范数优化的ALM算法描述如下。
构造增广拉格朗日函数为式(11)
(11)
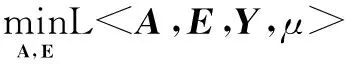
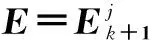
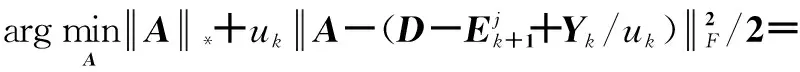
(12)
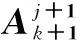
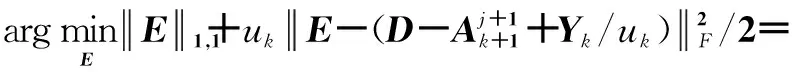
(13)
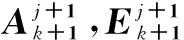
(14)
uk的更新公式为
(15)
式中:ρ>1,为常数;ε>0为较小的正数。
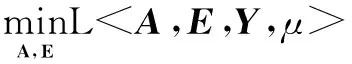
D1/uk(D-Ek+1+Yk/uk)
(16)
Sλ/uk(D-Ak+1+Yk/uk)
(17)
EALM与IELAM区别在于EALM收敛于Qlinearly最优解决方案,每次迭代只计算矩阵中部分块的SVD。IELAM针对整个矩阵进行计算SVD,可能收敛于次优解。
ALM算法可以概括为:
(18)
输入参数λ,u0>0,ρ>1,k=0。
重复。
2)(U,S,V)=svd(D-Ek+Yk/uk)
(19)
3)Ak+1=D1/uk(D-Ek+1+Yk/uk)
(20)
4)Ek+1=Sλ/uk(D-Ak+1+Yk/uk)
(21)
5)Yk+1=Yk+(D-Ak+1-Ek+1)
(22)
6)按式(15)更新uk,直到收敛。
7)输出低秩矩阵A和稀疏误差矩阵E。
通过分析求解低秩矩阵最小核范数优化问题的过程,可以得出如下结论:
在低秩矩阵核范数矩阵优化问题中,当核范数收敛时,此时矩阵奇异值很小,使恢复出的低秩矩阵最大程度地保留了原始矩阵信息,因而可以达到修复矩阵受损数据的目的。同时,用误差矩阵1范数最优解代替0范数最优解,使得当低秩矩阵优化问题收敛时,误差矩阵尽可能地稀疏,误差矩阵越稀疏低秩矩阵恢复的效果越好。
在运用矩阵低秩矩恢复算法阵去除噪声和恢复数据时,根据矩阵有用信息的低秩特性和误差的稀疏特性,并不要求噪声源要满足某一特定的噪声分布,因而在各种噪声下,用低秩矩阵恢复算法能达到去噪和数据恢复的双重作用。
为了更好地比较EALM算法和IEALM算法的性能,对一图片增加噪声密度为0.2的椒盐噪声进行对比实验。两种算法的运行结果如图1所示,图1中所示图片实际大小为(350,490)。EALM恢复图像的PSNR为24.22dB,运行时间为232.94s。IEALM恢复图像的PSNR值为24.21dB,运行时间为6.26s。由此可见,EALM算法运行时间较IEALM算法增加较大,而PSNR值增加较小。在本文中选取IEALM算法进行图像核矩阵优化问题的求解。

图1 EALM和IEALM恢复结果比较
本文算法流程如下:
1)图像矩阵进行小波分解,高频系数用阈值法重构。
2)用重构的小波系数矩阵进行图像重构,完成小波阈值去噪处理。
3)对处理后的图像矩阵用IELAM算法进行核范数优化,将其分解为低秩矩阵和误差矩阵。
4)输出恢复出的低秩矩阵和稀疏误差矩阵。
4仿真结果及分析
本文算法所使用图片如图2所示。

图2本文所使用实验图片
对上述图2a增加噪声密度density=0.1的椒盐噪声后,用本文算法去噪后的图片如图3所示。

图3 图像去噪比较1
图像矩阵I增加乘性噪声公式如下
J=I+vI
(23)
对图2d增加系数v=0.1的乘性噪声时,本文算法去噪效果如图4所示。

图4 图像去噪比较2
对Lena图增加u=0,σ=0.1的Gaussian噪声后,本文算法去噪效果如图5所示。

图5 图像去噪比较3
从图3~5可以看出本文算法比传统单一小波阈值算法去噪获得了更好的视觉特性和更大信噪比。小波阈值去噪虽然能够去除图像的噪声,但是在重构小波系数的时候,引入了量化噪声。小波阈值选取不当还可能破坏图像本身有用的信息,大噪声环境下,要尽可能多地去除噪声,就要选择大的阈值才能达到较好的去噪效果。选取阈值过大将会去除图像本身有用的信息,造成图像信息缺失和信噪比下降。在小波去噪引入量化噪声和去噪过程中损害了原始数据时,利用低秩矩阵恢复算法来恢复受损的图像本身的有用信息,同时又进一步去除低频部分噪声和量化噪声,从而达到比单一小波阈值去噪更好的去噪效果。
在PSNR对比上,本文进行的的对比实验结果如图6~8所示。
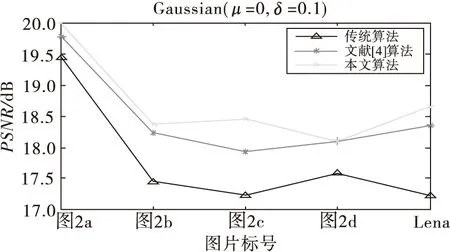
图6 高斯噪声下的PSNR对比

图7 椒盐噪声下的PSNR对比

图8 乘性噪声下的PSNR对比
进一步分析去噪结果比较图和PSNR对比结果。从图3可以看出,在椒盐噪声环境下,本文算法去噪的视觉特性要明显优于单一的小波阈值算法,图7的实验结果也验证了这个结论。从图4、图5和PSNR对比结果可以看出,在乘性噪声和高斯噪声环境下,本文算法本文算法都不但有最好的视觉特性而且还有最高PSNR。可以看出,在种多噪声环境下本文算法都达到了预期去噪和修复受损数据的目的,算法性能都好于单一的小波阈值去噪。
5结束语
本文提出了一种融合小波变换与低秩矩阵恢复的图像去噪算法,针对小波阈值算法会引入量化噪声和去噪过程未考虑低频噪声,阈值选取不当会损害图像有用信息的这两个问题,在小波去噪的基础上,结合低秩矩阵的最小核范数约束的方法基本解决了上述两个问题,并且实验结果已经验证了本文所提出算法的有效性和可行性。但是在实验中发现,在高斯噪声环境下本文算法PSNR提高并不大,如何提高在高斯噪声条件下本文算法的性能是将来所要进一步研究的问题。同时,本文低秩矩阵恢复算法基于奇异值分解,算法求解效率不是最优,如何提高本文算法的运行效率也将是下一步研究的重点。
参考文献:
[1]翟东海,鱼江,段维夏,等.米字型各向异性扩散模型的图像去噪算法[J].计算机应用, 2014,34(5):1494-1498.
[2]朱华生,邓承志.自适应Shearle域约束的全变差图像去噪[J].计算机工程,2013,39(1):221-224.
[3]刘平.基于小波变换的边缘保留图像去噪改进算法[J].电视技术,2014,38(5):13-15.
[4]金显华,赵元庆.改进的阈值图像去噪算法仿真研究[J].计算机仿真,2012(1):191-194.
[5]刘毅文,李玲玲,李翠华,等.基于小波多阈值和子带增强的图像去噪[J].厦门大学学报(自然科学版),2012,51(3):342-347.
[6]刘冶,朱蔚恒,潘炎,等.基于低秩和稀疏矩阵分解的多源融合链接预测算法[J].计算机研究与发展,2015,52(2):423-436.
[7]BECKA,TEBOULLEM.Afastiterativeshrin-kagethresholdingalgorithmforlinearinverseproblems[J].SIAMjournalonimagingsciences,2009,2(1):183-202.
[8]LINZC,GANESHA,WRIGHTJ,etal.Fastconvexoptimizationalgorithmsforexactrecoveryofacorruptedlowrankm-atrix[EB/OL].[2015-07-12].http://perception.csl.illinois.edu/matrix-rank/Files/rpca_algorithms.pdf.
[9]LIANGX,RENX,ZHANGZD,etal.Europeanconferenceoncomputervision(ECCV)[EB/OL].[2015-07-12].http://eccv2012.unifi.it/.
[10]ZHENGZL,YUMD,JIAJ,etal.Fisherdiscriminationbasedlowrankma-trixrecoveryforfacerecognition[J].Patternrecognition,2014(47):3502-3511.
New image denoising algorithm based on wavelet transform and low rank matrix recovery
WU Junqin,WU Liang
(SchoolofInformationEngineering,JiangxiUniversityofScienceandTechnology,JiangxiGanzhou341000,China)
Abstract:Aiming at the problem of image denoising based on the wavelet threshold introduced the quantization noise, the threshold selected may lose the useful information of the image itself.An image denoising algorithm based on wavelet transform and low rank matrix recovery (LRMR) is proposed. Different from a single threshold denoising algorithm, the algorithm can eliminate the more noise and fixs the corrupted data, and can adapt to various noise environment. Firstly, select the fixed threshold to carry on the wavelet denoising to preprocess the image matrix. Then the augmented Lagrange multiplier algorithm minimize the kernel matrix norm,and the preprocessed matrix factorized into a low rank approximation matrix and a sparse error matrix. Experiments results show that the proposed algorithm has better performance and robustness under different noise condition.
Key words:wavelet transform;image denoising;agumented lagrange multiplier;low rank matrix recovery;minimize the kernal norm
中图分类号:TP301
文献标志码:A
DOI:10.16280/j.videoe.2016.03.004
基金项目:国家自然科学基金项目(11062002)
作者简介:
吴君钦(1966— ),副教授、硕士生导师,研究领域为信号与信息处理、嵌入式;
邬亮(1990— ),硕士生,研究领域为模式识别与人工智能。
责任编辑:时雯
收稿日期:2015-08-15
文献引用格式:吴君钦,邬亮.新融合小波变换与低秩矩阵恢复图像去噪算法[J].电视技术,2016,40(3):17-21.
WU J Q,WU L.New image denoising algorithm based on wavelet transform and low rank matrix recovery[J].Video engineering,2016,40(3):17-21.
