矩形管道内低雷诺数圆柱绕流尾迹演化特性

董振营，周本钊，孙志强，蒋赟，周天(中南大学 能源科学与工程学院，湖南 长沙，410083)



矩形管道内低雷诺数圆柱绕流尾迹演化特性

董振营，周本钊，孙志强，蒋赟，周天
(中南大学 能源科学与工程学院，湖南 长沙，410083)

摘要：为了揭示有限管道壁面对圆柱绕流尾迹演化特性的影响，采用基于有限容积法的数值模拟方法，对矩形管道内雷诺数为100的三维圆柱绕流尾迹流场进行计算分析，探讨阻流比和长径比对圆柱表面和尾迹流场中压力分布的影响。研究结果表明：圆柱前、后驻点的压力系数受展向位置影响较大，后驻点压力系数与旋涡脱落状态有关；时均压力系数受管道端壁影响显著，沿前驻点至后驻点圆柱表面时均压力系数先减小后增大；在远离端壁一定区域内，尾迹流态为涡街；而在靠近端壁的一定区域内，尾迹呈现出近似双子涡形态；圆柱表面相同位置处的时均压力系数基本上随阻流比的增大而增大，随长径比的增大而减小。

关键词：圆柱绕流；尾迹演化；矩形管道；雷诺数

流体绕过非流线形柱体广泛存在于能源动力系统的多个关键生产环节之中，如管式换热器中介质横掠受热管、热电偶测温时介质冲刷保护套管等[1]。流体与柱体之间的相互作用极其复杂，其中涉及流动分离、旋涡脱落、升力振荡等非线性过程[2−4]，因此，深入认识钝体绕流规律及其尾迹流场演化特性，不仅对流体力学研究具有重要的理论价值，而且对提高存在钝体绕流的工业设备安全性也具有实际意义。国内外学者对钝体绕流进行了大量的研究，如：WILLIAMSON[5]通过研究指出圆柱绕流边界层存在层流、层流向湍流过渡、湍流等多种形态；张孝棣等[6]利用 PIV 技术观测圆柱尾迹的速度场和涡量场，发现在一定雷诺数范围内旋涡形成区随雷诺数减小；YANG 等[7]采用有限元法模拟了流体绕流振动方柱，发现柱体回流区随振动速度增加而被压缩，且阻流比对尾迹流场有显著影响；MITTAL[8]发现当分流板长度超过2倍圆柱直径后，分流板能够抑制旋涡脱落；SEN 等[9]采用有限容积法发现壁面使得圆柱绕流临界雷诺数增大；LANKADASU 等[10]发现圆柱绕流临界雷诺数随来流剪切参数增大而减小，但随阻流比增大而增大；REHIMI 等[11]发现壁面会使旋涡脱落的三维特性受到抑制，阻流比越大，旋涡脱落的三维特性会在更大的雷诺数下出现；孙志强等[12]采用RNG k−ε模型研究了管道内钝体尾迹流场和旋涡脱落的稳定性和旋涡形成及脱落过程，分析了壁面静压随旋涡演化的情况；桑文慧等[13]采用不同离散格式和耦合算法对有限流道内的圆柱绕流进行了数值模拟，得到了优化的算法组合。在上述研究中，大多数是针对钝体长径比很大的情况展开的，并假设尾迹流场仅受侧壁的影响，将尾迹流场常简化为二维[14]。然而，实际钝体绕流一般都发生在有限管道内，端壁对尾迹流场的影响不容忽视，长径比也是重要影响因素，此时，尾迹流场必须考虑三维演化。但目前对有限管道圆柱绕流演化特性的研究还不够深入，部分问题(如端壁对展向旋涡的抑制作用等)并未得到很好解决。为此，本文作者采用数值模拟方法，对矩形管道内雷诺数为100 的三维圆柱绕流尾迹流场进行分析，着重探讨阻流比和长径比对圆柱表面和尾迹流场中压力分布的影响。

1　物理模型与数值求解

所研究的矩形管道内圆柱绕流物理模型如图1所示。直径为d的圆柱体固定于矩形管道两侧壁的中间，流体从左至右横掠圆柱。流体入口至圆柱中心的距离为L1，圆柱中心到流体出口的距离为L2，流道宽度为W，流道高度为 H。圆柱相对于流道的阻流比β 定义为

圆柱的长径比γ定义为

以圆柱直径 d 为特征长度，对其他长度进行量纲一处理，对应的量纲一变量用“*”表示。计算域的坐标原点位于圆柱中心，量纲一坐标值定义为x*=x/d，y*=y/d，z*=z/d，则本研究的计算区域范围为：–10≤x*≤30，–0.5/β≤y*≤0.5/β，–0.5/γ≤z*≤0.5/γ。

采用空气作为流动介质，其密度ρ=1.225 kg/m3，动力黏度μ=1.789 4×10−5N∙s/m2。由于研究的雷诺数Re=100(以圆柱直径作为特征长度)，故空气流动为层流且压缩性可忽略。其控制方程包括连续性方程和Navier−Stokes方程，即

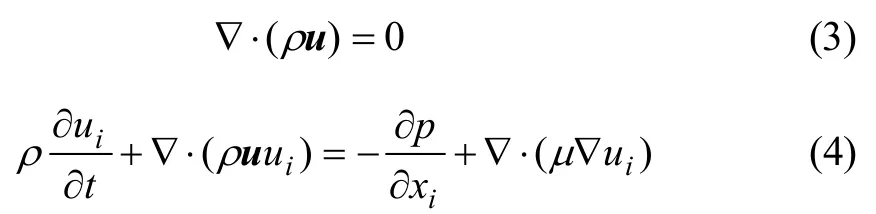
式中：u为速度矢量；t为时间；p为压力。

图1　矩形管道内圆柱绕流物理模型Fig.1　Physical model of flow aroundCircularCylinder in rectangularChannel

流体入口采用Dirichlet边界条件，雷诺数通过设定流体入口速度而改变。圆柱表面及其四周壁面均设定为固定无滑移。由于流道足够长，可认为流动在出口处已充分发展，故在流体出口处采用Neumann 边界条件。根据桑文慧等的[13]研究结果，层流圆柱绕流动量方程采用 QUCIK 格式进行离散，非稳态项采用二阶隐式格式进行离散，压力项采用Standard格式进行离散，压力速度采用SIMPLEC算法耦合。

考虑到圆柱绕流的流动特性，采用基于有限容积法的多块网格方案。首先，将矩形流道沿圆柱的横截面划分为前区、前影响区、圆柱区、侧影响区、尾迹区、后区共6个子区域。其中，圆柱区采用非正四边形O型网格，其余均采用正四边形网格。前区网格沿流动方向逐渐变密而后区网格逐渐变稀，对前影响区、侧影响区、尾迹区均进行局部加密。在完成网格无关性验证后，确定圆柱横截面计算域的网格数约为 31万。根据ZHANG等[15]对低雷诺数圆柱绕流的研究结果，确定圆柱展向上的网格节点间距为 0.4d，进而生成整个矩形流道计算区域的三维网格。

2　数值模拟结果验证

为了对数值求解算法和网格划分方案的准确性进行验证，定义斯特劳哈尔斯St、阻力系数CD和升力系数CL等圆柱绕流旋涡脱落特征参数，其计算式分别为

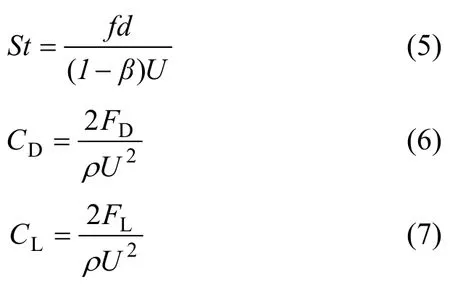
式中：f 为旋涡脱落频率；U 为来流平均速度；FD和FL分别为圆柱所受阻力和升力。对准无限流场的矩形管道(W*=H*=40)内 Re=100 的圆柱绕流进行模拟计算，提取斯特劳哈尔数St、时均阻力系数CDavg、升力系数均方根CLrms等特征参数，并将它们分别与文献值进行比较，结果如表1所示。从表1可见这 3个特征参数与参考值的相对误差均在±2%以内，表明所采用算法和网格具有较高的可靠性。

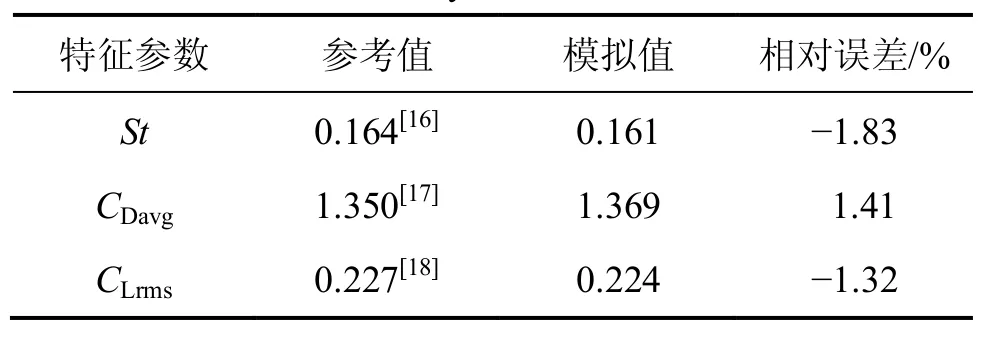
表1　圆柱绕流特征参数验证Table1　Validation ofCharacteristic variables for flow aroundCylinder

3　结果与讨论

为了定量描述圆柱表面的受力情况，对于任一圆柱横截面，建立以圆柱中心为原点、前驻点为起点的极坐标体系，圆柱表面任一点用其极角θ进行描述。规定顺时针方向为正，则圆柱前驻点 θ=0°，后驻点θ=180°。定义圆柱表面任一点的压力系数为

式中：p(θ)为圆柱表面极角为 θ处的静压；p0为出口处静压。

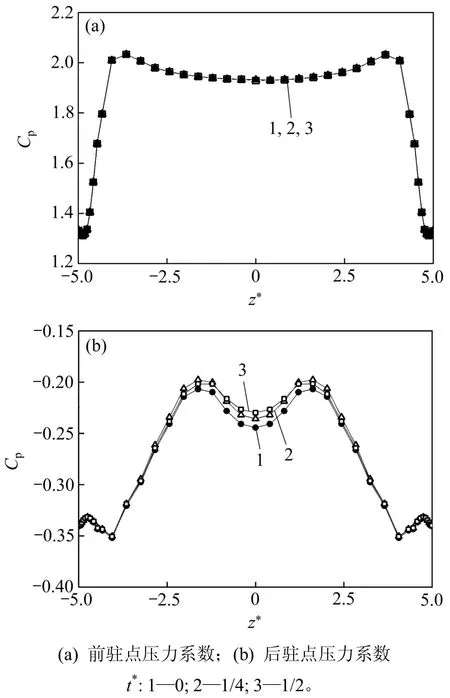
图2圆柱前、后驻点的压力系数CpFig.2PressureCoefficient at the front and rear stagnation point

3.1圆柱表面压力分布

图2所示为不同时刻t下β=0.100和γ=10时的圆柱前、后驻点压力系数沿展向的分布，其中 t*=t/T(T为旋涡脱落周期)。从图2(a)可见：前驻点压力系数几乎不随时间变化，但受展向位置的影响较大；前驻点压力系数在圆柱上下端壁面处最小，然后急剧增大；当离开端壁一定距离(z*=±3.5)时，其值达到最大，之后略有减小。这是因为在前驻点处流体动压转变为静压，端壁边界层的存在使得邻近流体的动能因摩擦耗散，故这段距离内的前驻点压力系数显著减小。从图2(b)可见：圆柱后驻点压力系数沿展向呈马鞍形分布，分别在z*=±1.6和z*=±4.0附近达到最大值和最小值。造成这一马鞍形分布的原因可能是端壁的存在改变了其邻近的尾迹旋涡流态，使得后驻点压力系数出现明显的分段分布。与前驻点有所不同，后驻点压力系数除了受展向位置的影响外，还与旋涡脱落状态(时刻)有关。

图3所示为β=0.100和γ=10时圆柱表面的时均压力系数Cp分布情况。由于旋涡脱落的周期交替性，圆柱表面的时均压力系数关于流动方向对称，故仅给出圆柱一半表面的压力系数。从图3可见：当θ=0°～90°时，不同展向位置的时均压力系数均减小；而当θ=90°～180°时，时均压力系数则稍增大；在展向中心平面一定范围内(z*=0～4.0)，圆柱表面时均压力系数的分布基本重合；而在端壁(z*=5.0)处，时均压力系数出现了不同的分布状态。经进一步比较发现：当θ＜45°时，端壁处的时均压力系数小于展向中心平面处的时均压力系数；在 45°＜θ＜113°范围内端壁处的时均压力系数比中心平面处的大，而当 θ＞113°时，端壁处的时均压力系数又比中心平面处的小。

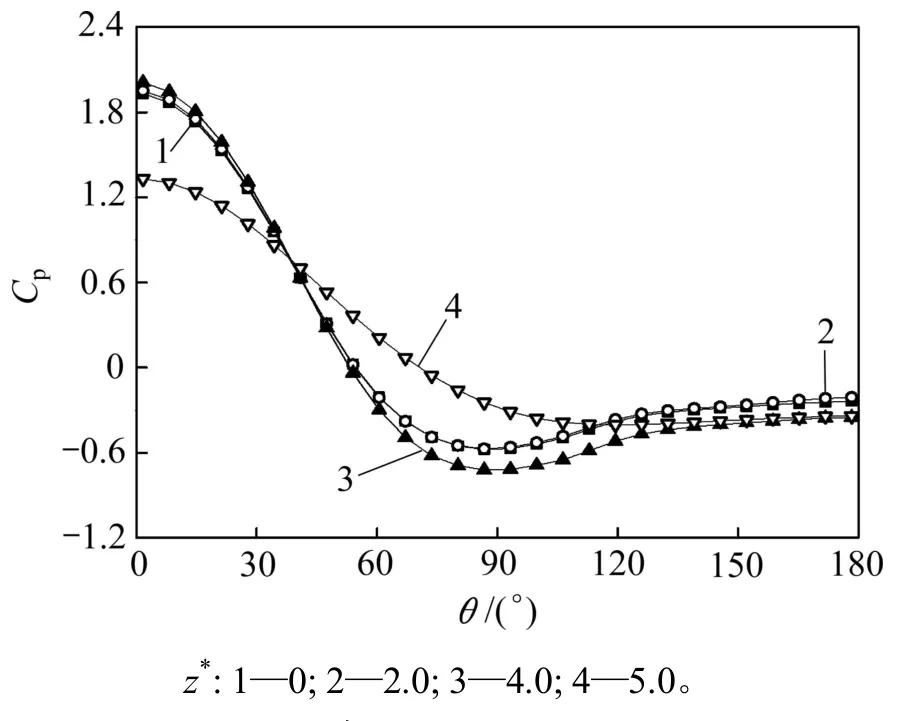
图3　圆柱表面的时均压力系数分布Fig.3　Time-averaged pressureCoefficient distribution alongCylinder surface

3.2尾迹流场压力分布及旋涡演化

图4所示为β=0.100和γ=10时尾迹流场中不同位置的时均压力系数分布。由于坐标原点位于圆柱中心，故所有监测点的压力起始于 x*=0.5。从图 4(a)可知：在纵向中心平面(y*=0)内圆柱后部一定距离内，压力系数沿流动方向迅速升高，在x*=5.0附近达到最大，而后压力系数沿流动方向逐渐减小；在靠近端壁(z*=4.0～5.0)处，时均压力系数达到最大后呈近似直线下降，而在纵向中心平面附近(z*=0～2.0)，时均压力系数波动较显著。这是由于尾迹旋涡的周期性脱落主要发生在纵向中心平面附近，流向上同时分布着多个不同时刻脱落的旋涡，旋涡中心处的压力较其周围的低，从而形成波动下降的趋势；而在端壁附近，由于壁面的阻碍作用，在一定展向距离内并无旋涡脱落，故其压力系数呈近似直线下降趋势。由图 4(b)可知：圆柱展向中心平面(z*=0)上不同横向位置处的时均压力系数沿流动方向波动下降，在 y*=2 处其值波动幅度最大；在距侧壁一定范围(y*=4～5)内，时均压力系数沿流动方向的变化趋势基本相同。

图5所示为β=0.1.00和γ=10时不同展向位置尾迹旋涡的流线和涡量分布。从图 5可看出：不同展向位置处圆柱绕流的尾迹形态存在较大差异。这是由于受端壁的影响，绕流圆柱的流体速度沿圆柱展向方向分布不均匀，导致绕流圆柱后不同展向位置的尾迹不同。在远离端壁的一定区域(z*=0～2.0)内，尾迹流态为涡街(见图 5(a)和图 5(b))；而在靠近端壁的一定区域(z*=4.0～ 4.5)内，尾迹呈现出近似双子涡形态(见图5(c)和5(d))。

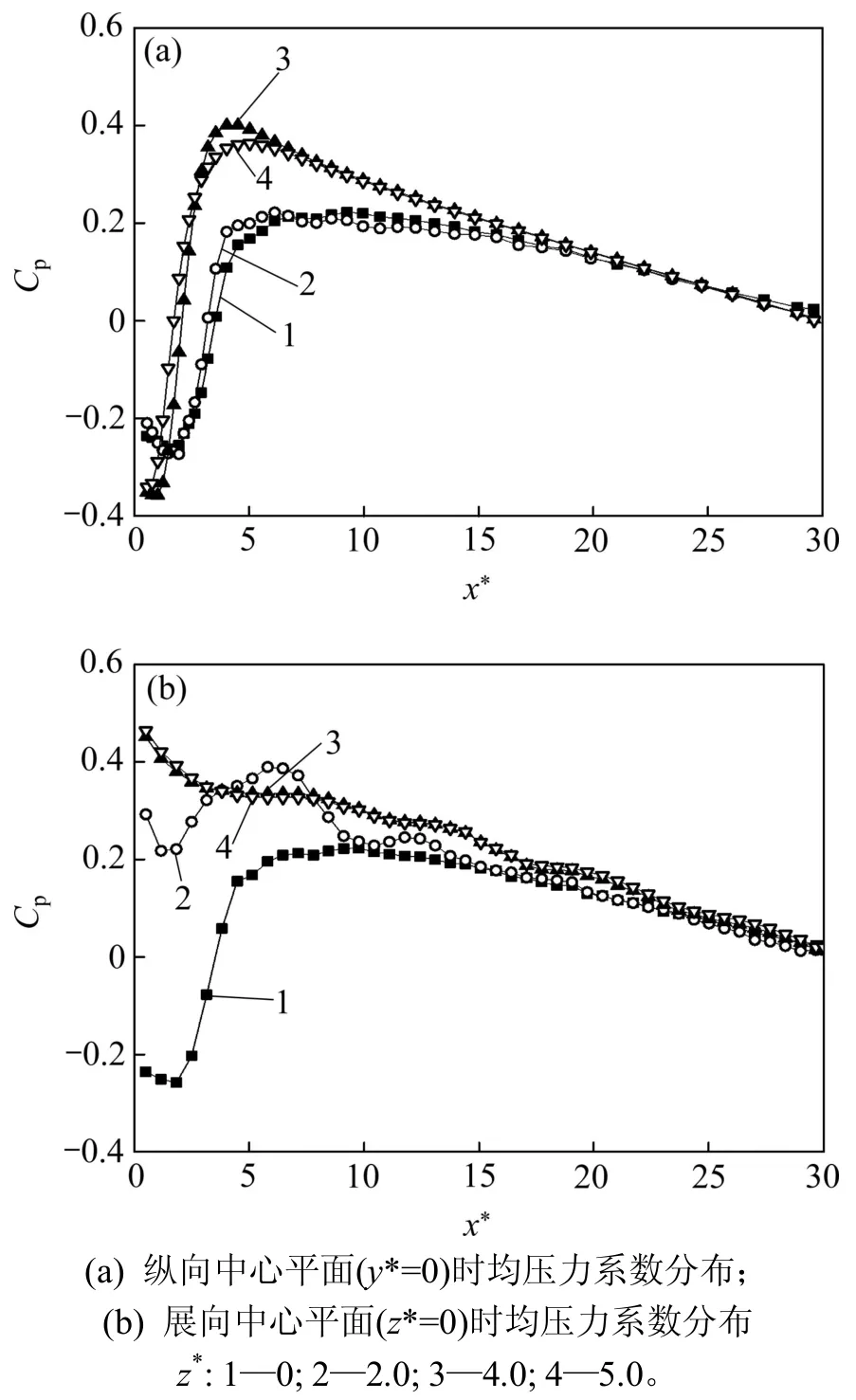
图4尾迹流场的时均压力系数分布Fig.4Time-averaged pressureCoefficient distribution in wake

3.3阻流比和长径比的影响

图6所示为不同阻流比和长径比时展向中心平面(z*=0)上圆柱表面的时均压力系数分布。图6(a)中，圆柱长径比固定为γ=10，可见圆柱表面时均压力系数在前驻点(θ=0°)最大，由于黏性作用，其值随 θ增大而减小，在θ≈80°时达到最小，之后又随θ增大而增大；在 β=0.050～0.100 范围内，阻流比越小，相同 θ处的时均压力系数也越小；但对于 β=0.025 的情形，其时均压力系数在θ＞35°后开始快速增大，逐渐超过其他阻流比时相同 θ位置处的时均压力系数。图 6(b)所示为 β=0.100 时不同长径比下展向中心平面上圆柱表面的时均压力系数分布。从图 6(b)可见：长径比对时均压力系数的影响与阻流比的影响相反，总体上看，在相同 θ位置，长径比越小，圆柱表面时均压力系数越大，仅对于γ=20的情形略有例外。

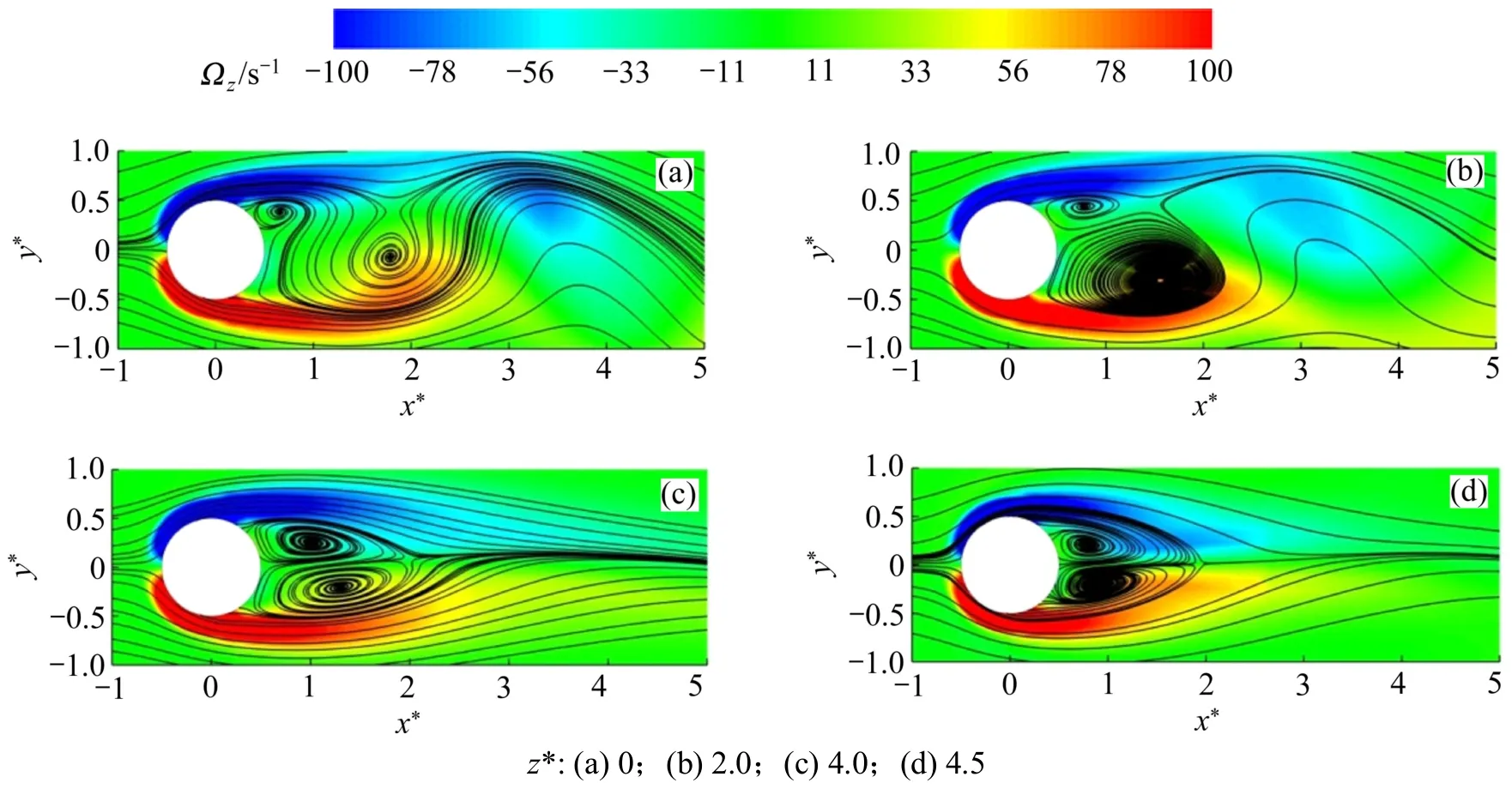
图5　不同展向位置处尾迹旋涡的流线与涡量Fig.5　Flow path-lines and vorticity in wake at different axial locations

图6　展向中心平面(z*=0)上圆柱表面时均压力系数分布Fig.6　Time-averaged pressureCoefficient distribution alongCylinder surface for theCentral axial plane(z*=0)

4 结论

1)矩形管道内圆柱绕流的前驻点压力系数几乎不随时间变化，但受展向位置的影响较大；而后驻点压力系数除了受展向位置的影响外，还与旋涡脱落状态(时刻)相关。时均压力系数受管道端壁影响显著，其值沿前驻点至后驻点圆柱表面先减小后增大。

2)在尾迹流场中，纵向中心平面内圆柱表面时均压力系数沿流向先迅速升高后逐渐减小，在展向中心平面上圆柱表面时均压力系数沿流向波动下降。在远离端壁的一定区域内，尾迹流态为涡街；而在靠近端壁的一定区域内，尾迹呈现出近似双子涡形态。

3)阻流比和长径比对圆柱尾迹流场的影响作用相反，圆柱表面相同位置的时均压力系数基本上随阻流比的增大而增大，却随长径比的增大而减小。

参考文献：

[1]涂福炳,武荟芬,张岭,等.径向热管换热器壳程数值模拟及结构参数优化[J].中南大学学报(自然科学版),2012,43(5):1975−1983.TU Fubing,WU Huifen,ZHANG Ling,et al.Numerical simulation and structural parameters optimization in shell side of radial heat pipe heat exchanger[J].Journal ofCentral South University(Science and Technology),2012,43(5):1975−1983.

[2]LI Zhiyong,SUN Zhiqiang.Development of the vortex mass flowmeter with wall pressure measurement[J].Measurement Science Review,2013,13(1): 20−24.

[3]SUN Zhiqiang,LI Zhiyong,JIANG Yun,et al.Influence of bluff body shape on wall pressure distribution in vortex flowmeter[J].Journal ofCentral South University,2013,20(3): 724−729.

[4]LI Saiwei,SUN Zhiqiang.Harvesting vortex energy in theCylinder wake with a pivoting vane[J].Energy,2015,88: 783−792.

[5]WILLIAMSONC H K.Vortex dynamics in theCylinder wake[J].Annual Review of Fluid Mechanics,1996,28(1): 477−539.

[6]张孝棣,蒋甲利,贾元胜,等.圆柱体绕流尾迹的PIV测量[J].实验流体力学,2005,19(2): 74−78.ZHANG Xiaodi,JIANG Jiali,JIA Yuansheng,et al.Measurements ofCylinder’s wake by PIV[J].Journal of Experiments in Fluid Mechanics,2005,19(2): 74−78.

[7]YANG S J,CHANG T R,FU W S.Numerical simulation of flow structures around an oscillating rectangularCylinder in aChannel flow[J].Computational Mechanics,2005,35(5): 342−351.

[8]MITTAL S.Effect of a “slip” splitter plate on vortex shedding from aCylinder[J].Physics of Fluids,2003,15(3): 817−820.

[9]SEN S,MITTAL S,BISWAS G.Steady separated flow past aCircularCylinder at low Reynolds numbers[J].Journal of Fluid Mechanics,2009,620: 89−119.

[10]LANKADASU A,VENGADESAN S.Onset of vortex shedding in planar shear flow past a squareCylinder[J].International Journal of Heat and Fluid Flow,2008,29(4):1054−1059.

[11]REHIMI F,ALOUI F,NASRALLAH S B,et al.Experimental investigation of aConfined flow downstream of aCircularCylinderCentred between two parallel walls[J].Journal of Fluids and Structures,2008,24(6): 855−882.

[12]孙志强,张宏建,周孑民.涡街流量计内壁面压力分布的数值模拟[J].传感器与微系统,2008,27(10): 70−75.SUN Zhiqiang,ZHANG Hongjian,ZHOU Jiemin.Numerical simulation of wall pressure distribution in vortex flowmeter[J].Transducer and Microsystem Technologies,2008,27(10): 70−75.

[13]桑文慧,孙志强,周孑民.有限流道内低雷诺数二维圆柱绕流数值模拟[J].中南大学学报(自然科学版),2012,43(3):1166−1170.SANG Wenhui,SUN Zhiqiang,ZHOU Jiemin.Numerical simulation of two-dimensional flow around aCircularCylinder at low Reynolds numbers in finiteChannel[J].Journal ofCentral South University(Science and Technology),2012,43(3):1166−1170.

[14]蒋赟,孙志强,周孑民.阻流比对平行壁面间圆柱绕流尾迹演化的影响[J].中南大学学报(自然科学版),2015,46(11): 4355−4362.JIANG Yun,SUN Zhiqiang,ZHOU Jiemin.The effect of blockage ratio on the evolution ofCircularCylinder wake between parallel walls[J].Journal ofCentral South University(Science and Technology),2015,46(11): 4355−4362.

[15]ZHANG J,DALTONC.A three-dimensional simulation of a steady approach flow past aCircularCylinder at low Reynolds number[J].International Journal for Numerical Methods in Fluids,1998,26(9):1003−1022.

[16]WILLIAMSONC H K.Oblique and parallel modes of vortex shedding in the wake of aCircularCylinder at low Reynolds numbers[J].Journal of Fluid Mechanics,1989,206: 579−627.

[17]HENDERSON R D.Details of the dragCurve near the onset of vortex shedding[J].Physics of Fluids,1995,7: 2102.

[18]NORBERGC.Fluctuating lift on aCircularCylinder: Review and new measurements[J].Journal of Fluids and Structures,2003,17(1): 57−96.

(编辑 陈灿华)

Evolution ofCircularCylinder wake at low Reynolds number in rectangularChannels

DONG Zhenying,ZHOU Benzhao,SUN Zhiqiang,JIANG Yun,ZHOU Tian
(School of Energy Science and Engineering,Central South University,Changsha 410083,China)

Abstract:To reveal the effect ofConfinedChannel walls on the evolution ofCircularCylinder wake,numerical simulations based on the finite volume method wereConducted.The three-dimensional flow fields ofCircularCylinder wakes at Reynolds number100 in rectangularChannels wereComputed and analyzed.The influence of blockage and aspect ratios on the pressure distribution of theCylinder surface and in the wake was explored.The results show that the pressureCoefficients at the front and the rear stagnation points are affected by the positions in spanwise direction,and the pressureCoefficient at the rear stagnation point is associated with the vortex shedding state.The time-average pressureCoefficients are influenced markedly by theChannel’s end walls,and their values increase in the beginning and decrease afterward along theCylinder surface from the front to the rear stagnation point.The wake regime is the vortex street in the zone far from the end walls,whereas the wake becomes the twin vortices in the zone near to the end walls.The time-average pressureCoefficients ofCylinder surface at identical positions basically increase with the increase of blockage ratios,but decrease with the increase of aspect ratios.

Key words:flow aroundCircularCylinder;wake evolution;rectangularChannel;Reynolds number

中图分类号：O357.1

文献标志码：A

文章编号：1672−7207(2016)01−0273−06

DOI:10.11817/j.issn.1672-7207.2016.01.037

收稿日期：2015−06−10；修回日期：2015−08−08

基金项目(Foundation item)：国家自然科学基金资助项目(51006125)；中南大学教师研究基金资助项目(2013JSJJ018)(Project(51006125)supported by the National Natural Science Foundation ofChina; Project(2013JSJJ018)supported by the Teachers Research Foundation ofCentral South University)

通信作者：孙志强，博士，教授，从事多相流测试技术、新能源与节能技术研究；E-mail: zqsun@csu.edu.cn