雷诺数对涡桨飞机增升装置气动特性影响的计算研究
2016-12-19许瑞飞钱瑞战雷武涛
许瑞飞,钱瑞战,雷武涛
(中国航空工业集团公司 第一飞机设计研究院,西安 710089)
雷诺数对涡桨飞机增升装置气动特性影响的计算研究
许瑞飞,钱瑞战,雷武涛
(中国航空工业集团公司 第一飞机设计研究院,西安 710089)
雷诺数是表征流体粘性对流动影响的相似参数,对飞机部件的气动性能具有重要的影响。利用商业软件CFX对某民用涡桨飞机增升装置构型进行变雷诺数计算研究,详细分析雷诺数对升力系数、失速特性以及附面层速度特性的影响。结果表明:雷诺数对最大升力系数和失速迎角都有显著的影响;不同雷诺数下机翼分离形态变化显著,大雷诺数下机翼分离区域较小;不同雷诺数下机翼附面层状态不一致,雷诺数增大使得附面层速度型更饱满,机翼的抗分离能力增强。
涡桨飞机;增升装置;雷诺数;气动特性
0 引 言
随着飞机和发动机技术的不断发展,涡桨飞机的巡航速度逐渐提高,在400 nmile的航段上运营的经济性明显高于喷气式飞机。这一技术优势有助于航空公司开辟新市场。采用主动噪声和振动抑制系统,涡桨飞机的客舱内部噪声大幅降低,乘客舒适性显著提高。因此在高频率、短航程及低成本市场上涡桨飞机有很大的发展空间。
涡桨飞机的设计过程需要掌握一些关键技术。其中,复杂增升装置的设计技术[1-3]是气动设计的关键技术之一,直接影响着飞机的起飞距离、着陆距离、起飞重量等[4]。在增升装置气动性能的影响因素中,雷诺数是一个十分重要的参数,它表示为惯性力与粘性力之比,是一个表征流体粘性对流动影响的相似参数,对增升装置气动性能有显著影响。
国外型号设计单位如波音、空客等都对雷诺数影响规律进行了大量的研究。F.M.Payne等[5]通过NTF风洞对B777-200飞机的起飞和着陆构型进行了变雷诺数试验,并利用MDOE方法对外襟翼缝道参数进行了变雷诺数研究。M.M.Curtin等[6]对B777飞机进行了不同雷诺数的测力和测压试验研究,并将飞行雷诺数得到的试验数据与试飞数据比较,试图建立风洞试验数据至试飞数据的修正。R.W.Clark等[7]对MD-11飞机巡航状态进行了变雷诺数研究,并详细分析了不同雷诺数下升力、阻力和力矩系数的变化。J.Quest等[8]利用ETW风洞对空客某高升力构型进行了高雷诺数风洞试验,以探索雷诺数影响规律。为了研究雷诺数对飞机的影响规律,欧洲EUROLIFT计划专门针对某高升力构型进行雷诺数影响研究[9-10]。郑隆乾等[11]对某民用飞机增升装置着陆构型进行了半模高雷诺数风洞试验,获得了不同马赫数下的雷诺数影响。
雷诺数对增升装置气动特性有显著影响。升力系数、阻力系数、升阻比等气动参数在飞机设计中极为重要,直接关系到型号设计的成败。因此,研究雷诺数对增升装置的影响具有现实意义,研究成果可直接应用于型号设计。
本文利用CFD技术对某涡桨飞机着陆翼身组合体构型进行数值模拟。首先将计算结果与试验数据进行对比,然后研究雷诺数对某涡桨飞机升力系数、失速特性以及附面层速度特性的影响,详细分析雷诺数对飞机气动特性的影响规律,以期为涡桨飞机气动力设计和风洞试验数据的相关性修正提供参考。
1 计算方法
国内外已经开展了有关增升装置的数值计算方法研究[12-15]。本文采用商业软件CFX进行飞机增升装置的数值模拟计算。CFX软件是基于有限元的有限体积法,用于求解雷诺平均N-S方程。基于有限元的有限体积法兼具有限体积法的守恒特性和有限元法的数值精确性。求解控制方程为
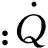
2 计算模型与网格
计算模型采用某民用涡桨飞机着陆翼身组合体构型。该飞机增升装置只有后缘襟翼,无前缘缝翼,如图1所示。
图1 某民用涡桨飞机着陆翼身组合体模型
计算网格采用H-O拓扑形式,在物面附近生成O型网格,远场采用H型网格。整个流场域网格变化率合适,疏密分布合理,过渡均匀,满足计算要求,表面网格如图2所示,网格量为2 000万左右。

图2 某民用涡桨飞机着陆翼身组合体构型表面网格
3 计算结果分析
3.1 计算与试验验证
测试算例采用某民用涡桨飞机风洞试验模型。试验模型只是在图1模型(即本文计算模型)的基础上对短舱进行了下移,其他部件数模无变化。计算网格生成与第2节类似。计算马赫数Ma=0.2,雷诺数Re=7.4×106,计算与试验结果的比较如图3所示。
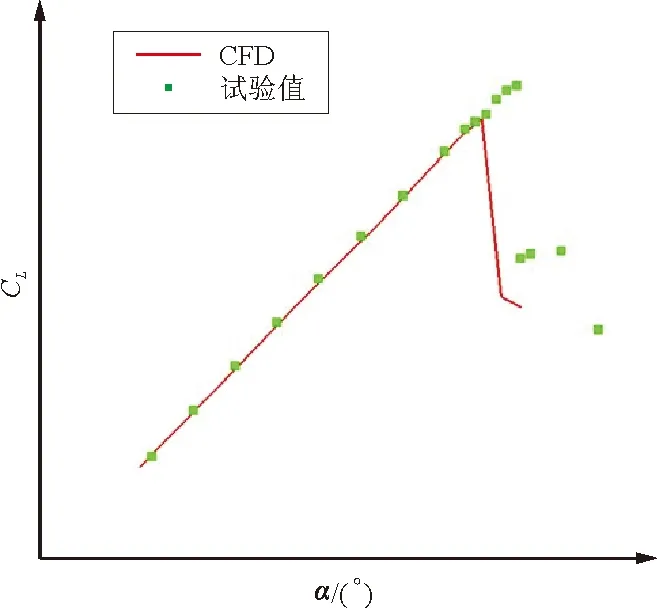
(a) 升力曲线
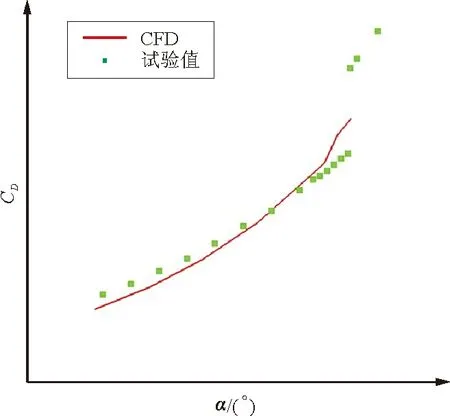
(b) 阻力曲线
从图3可以看出:计算得到的升力系数曲线与试验在小迎角吻合较好,失速迎角和最大升力系数值略有不同,失速发展趋势基本一致,表明本文计算方法能够很好地模拟增升装置的气动特性和流动特性。
3.2 不同雷诺数下力系数和压力分布比较
为了研究雷诺数对某民用涡桨飞机增升装置的影响,基于不同雷诺数(1.9×106,3.0×106,4.0×106,6.0×106,8.0×106,1.17×107)对着陆翼身组合体构型进行计算研究。计算马赫数Ma=0.2,不同雷诺数下某民用涡桨飞机着陆翼身组合体构型的升力系数和升阻极曲线如图4所示。
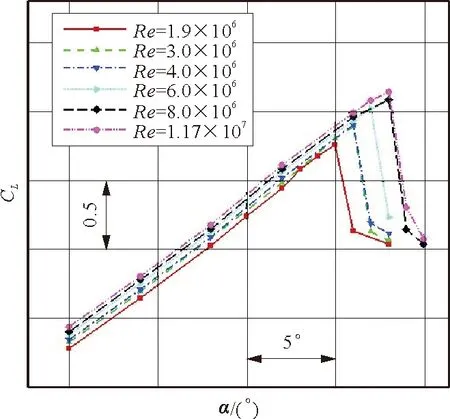
(a) 升力曲线
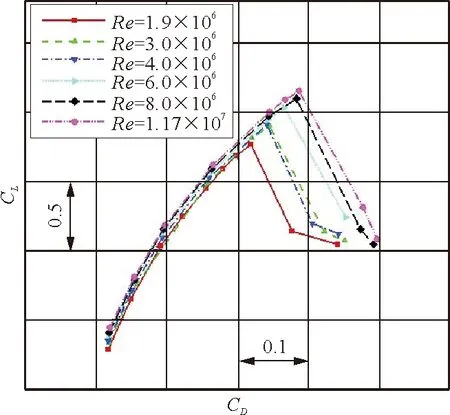
(b) 升阻极曲线
从图4可以看出:①随着雷诺数的增加,失速迎角和最大升力系数均显著增加;在小雷诺数下,升力系数的增长幅度比较大;随着雷诺数增加,粘性效应降低,最大升力系数的增长放缓,在小迎角下,升力系数获得提升,这主要是由于雷诺数的增加使得附面层厚度降低,飞机上的流动分离减轻,从而使得升力系数获得一定程度的增加,飞机失速迎角也推迟;②从图4(b)可以看出,在相同升力条件下,阻力降低,可以提高飞机的升阻比。
通过计算得到的某民用涡桨飞机最大升力系数和失速迎角随雷诺数的变化曲线如图5所示。
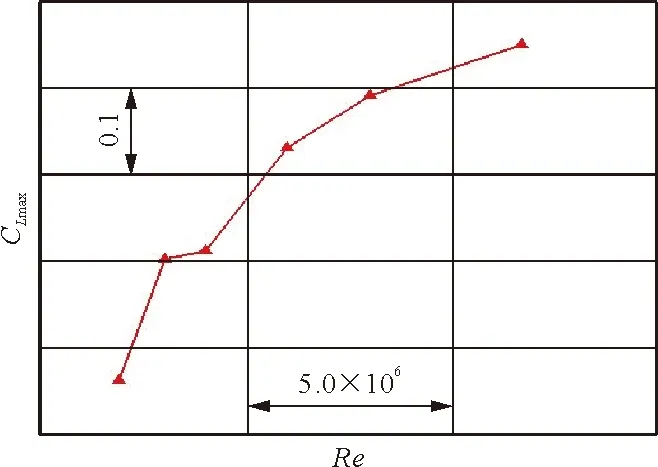
(a) 最大升力系数随雷诺数变化曲线
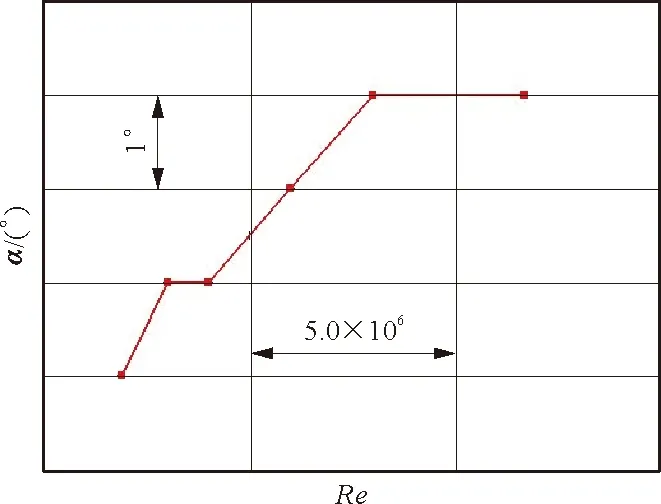
(b) 失速迎角随雷诺数变化曲线
从图5可以看出:随着雷诺数的增加,最大升力系数和失速迎角逐渐增加;在雷诺数为1.17×107时,最大升力系数达到最大值。
为了深入研究雷诺数对机翼气动特性的影响,截取机翼展向18.0%、43.0%、64.5%、82.0%站位的压力分布进行比较。迎角4°下不同雷诺数机翼展向站位压力分布比较如图6所示。
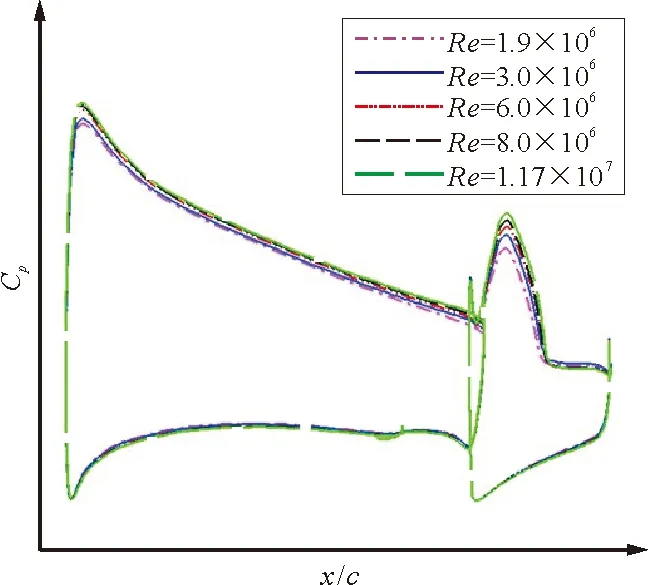
(a) 18.0%站位
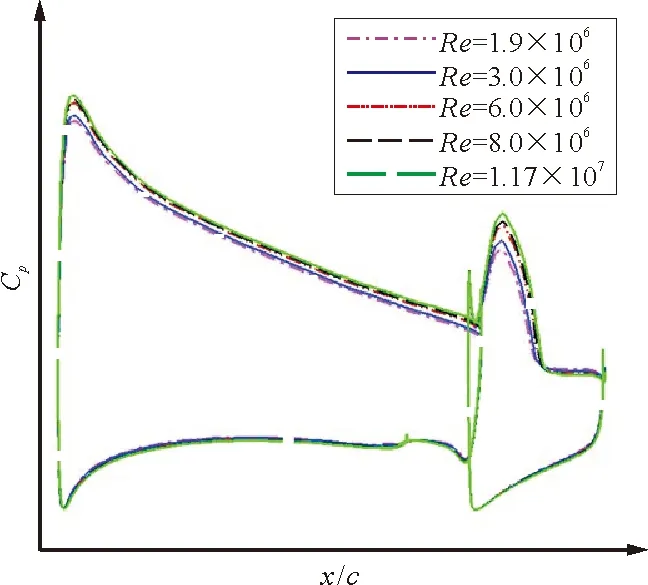
(b) 43.0%站位
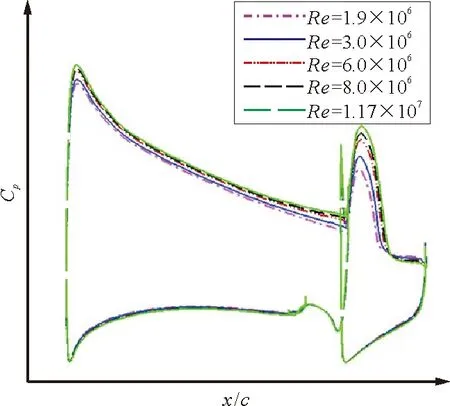
(c) 64.5%站位
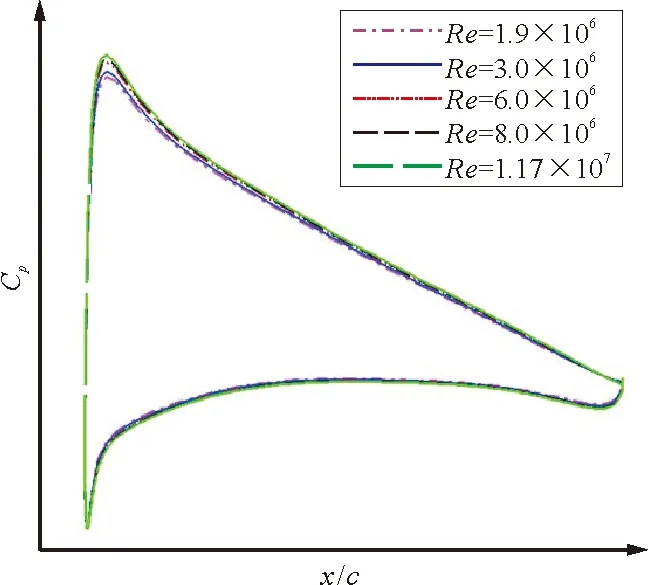
(d) 82.0%站位
从图6可以看出:随着雷诺数的增加,主翼和后缘襟翼的吸力峰值逐渐增大;主翼后缘压力恢复提升,襟翼上的流动分离区域逐渐减小,由此可对大雷诺数下升力系数较大的主要原因作出解释。
3.3 不同雷诺数下失速特性比较
迎角16°时着陆翼身组合体构型不同雷诺数下的表面压力云图和流谱如图7所示。
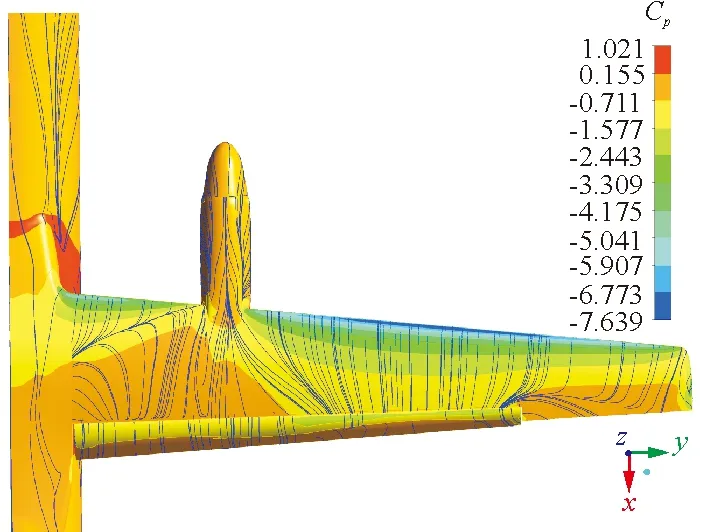
(a) Re=1.9×106
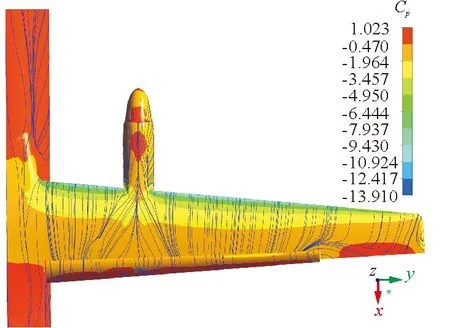
(b) Re=3.0×106
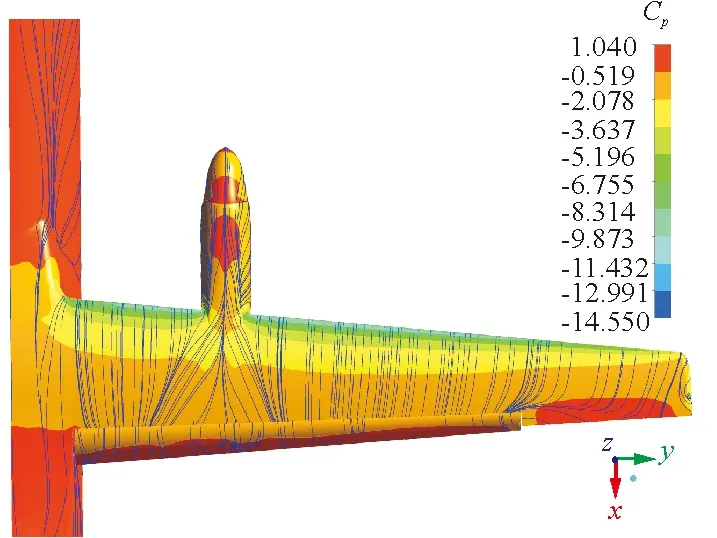
(c) Re=6.0×106
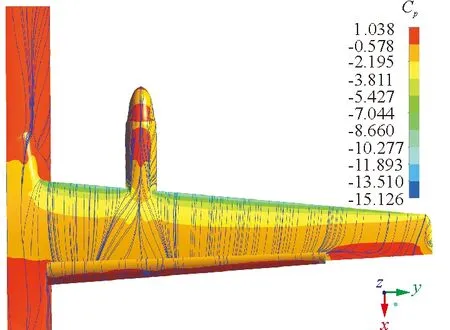
(d) Re=1.17×107
从图7可以看出:在小雷诺数1.9×106下机翼的中内侧出现了大面积的流动分离;当雷诺数增大到3.0×106,机翼上表面出现较小的流动分离,同时在短舱后面存在向机翼两侧扩展的横向流动;当雷诺数达到6.0×106以后,机翼上表面未出现明显的严重分离。
为了进一步理清机理,选择机翼后缘某点,截取当地速度型进行分析。迎角16°下不同雷诺数机翼后缘某点附面层速度型分布的比较如图8所示。
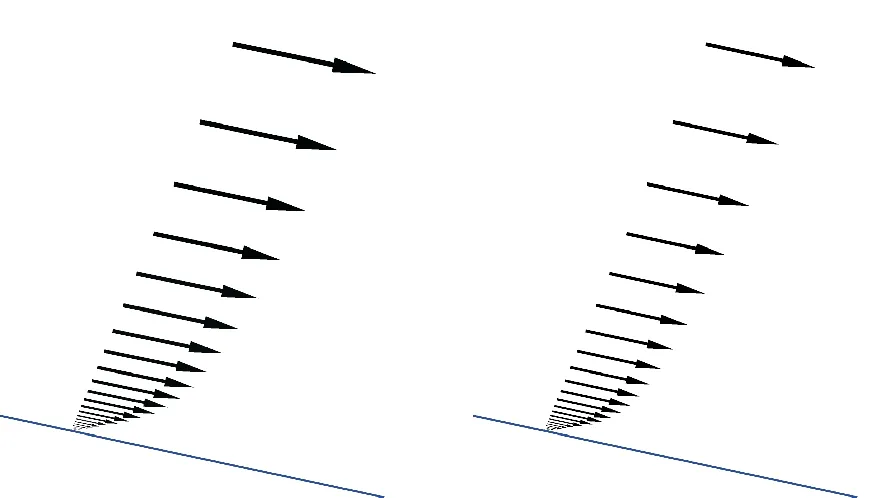
(a) Re=1.9×106(b) Re=3.0×106
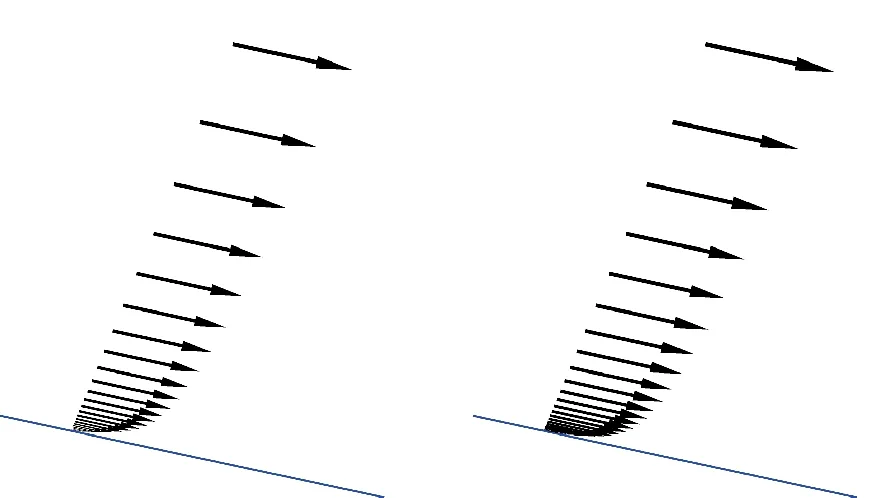
(c) Re=6.0×106(d) Re=1.17×107
图8 迎角16°下不同雷诺数机翼后缘某点附面层速度型比较
Fig.8ThecomparisonofvelocitydistributionfortrailingedgeofwingunderdifferentReynoldsnumberatangleofattack16°
从图8可以看出:当雷诺数为1.9×106时,此时当地附面层比较厚,接近壁面的速度值比较低;这种速度形态使得当地后缘很难抵抗较强的逆压梯度,容易造成流动分离;随着雷诺数的增加,当地速度型越来越饱满,接近壁面的速度也逐渐提高,使得壁面的抗分离能力增强;在大雷诺数下机翼能够抵抗较大的逆压梯度,分离较小,这也是在大雷诺数下机翼分离区域比较小的主要原因。
4 结 论
(1) 随着雷诺数的增加,失速迎角和最大升力系数均显著增加;飞机阻力降低,升阻比提高,气动性能显著增强。在大雷诺数下,升力系数的增长幅度明显放缓。
(2) 随着雷诺数的增加,主翼和后缘襟翼的吸力峰值逐渐增大;主翼后缘压力恢复提升,襟翼上的流动分离区域逐渐减小。负压峰值的提升和流动分离的减小是大雷诺数下升力系数较大的主要原因。
(3) 低雷诺数下,由于机翼后缘附面层较厚,附面层速度型不饱满,造成机翼后缘抗分离能力较弱,易于形成流动分离;随着雷诺数的增加,速度型更加饱满,抵抗逆压梯度能力增强,从而降低了流动分离区域。
(4) 不同雷诺数下某民用涡桨飞机分离形态不一致;大雷诺数下分离较小,但是总体来说,各雷诺数下分离位置基本一致,均在机翼短舱内侧开始分离。
综上所述,雷诺数对民用涡桨飞机增升装置气动特性有着显著影响。常规风洞的试验雷诺数很难达到飞行雷诺数,给气动数据的准确确定带来了一定的困难。因此建议在型号设计中,尽可能开展高雷诺数风洞试验,提高气动力数据的准确性。
[1]DamvanCP.Theaerodynamicdesignofmulti-elementhigh-liftsystemsfortransportairplanes[J].ProgressinAerospaceSciences, 2002, 38(2): 101-144.
[2] Wild J. Validation of numerical optimization of high-lift multi-element airfoils based on navier-stokes-equations[C]. AIAA-2002-2939, 2002.
[3] Kim S, Alonso J J, Jameson A. Multi-element high-lift configuration design optimization using viscous continuous adjoint method[J]. Journal of Aircraft, 2004, 41(5): 1082-1097.
[4] Smith A M O. High lift aerodynamics[J]. Journal of Aircraft, 1975, 12(6): 511-530.
[5] Payne F M , Wyatt G W, Bogue D R, et al. High Reynolds number studies of a Boeing 777-200 high lift configuration in the NASA ARC 12’ pressure tunnel and NASA LaRC National Transonic Facility[C]. AIAA-2000-4220, 2000.
[6] Curtin M M, Bogue D R, Om D, et al. Investigation of transonic Reynolds number scaling on a twin-engine transport[C]. AIAA-2002-0420, 2002.
[7] Clark R W, Pelkmant R A. High Reynolds number testing of advanced transport aircraft wings in the National Transonic Facility[C]. AIAA-2001-0910, 2001.
[8] Quest J, Hansen H, Mesuro G G. First measurements on an airbus high lift configuration at ETW up to flight Reynolds number[C]. AIAA-2002-0423, 2002.
[9] Rudnik R, Germain E. Re-No. scaling sffects on the EUROLIFT high lift configurations[C]. AIAA-2007-752, 2007.
[10] Rudnik R. Stall behaviour of the EUROLIFT high lift configurations[R]. AIAA-2008-0836, 2008.
[11] 郑隆乾, 陈迎春, 李亚林, 等. 某民机着陆构型雷诺数效应风洞试验研究[J]. 航空计算技术, 2012, 42(6): 70-71. Zheng Longqian, Chen Yingchun, Li Yalin, et al. Wind tunnel research about Reynolds number effects on landing configuration of a civil aircraft[J]. Aeronautical Computing Technique, 2012, 42(6): 70-71.(in Chinese)
[12] 朱自强. 应用计算流体力学[M]. 北京: 北京航空航天大学出版社, 1998. Zhu Ziqiang. Application computational fluid dynamics[M]. Beijing: Beihang University Press, 1998.(in Chinese)
[13] 朱自强, 陈迎春, 吴宗成, 等. 高升力系统外形的数值模拟计算[J]. 航空学报, 2005, 26(3): 257-262. Zhu Ziqiang, Chen Yingchun, Wu Zongcheng, et al. Numerical simulation of high lift system configuration[J]. Acta Aeronautica et Astronautica Sinica, 2005, 26(3): 257-262.(in Chinese)
[14] 左志成, 段卓毅. 运输类飞机高升力构型数值模拟研究[J]. 飞机设计, 2007, 27(1): 16-21. Zuo Zhicheng, Duan Zhouyi. Numerical simulation of high lift system for the transport aircraft[J]. Aircraft Design, 2007, 27(1): 16-21.(in Chinese)
[15] Dodbele S D. Three dimensional aerodynamic analysis of a high-lift transport configuration[R]. AIAA-93-3536, 1993.
(编辑:赵毓梅)
Numerical Investigation of Reynolds Number Effects on Aerodynamics Characteristics of High Lift System for Turboprop Aircraft
Xu Ruifei, Qian Ruizhan, Lei Wutao
(The First Aircraft Design and Research Institute, Aviation Industry Corporation of China, Xi’an 710089, China)
Reynolds number is one of the most useful similarity parameters in fluid dynamics which denotes the effect of the viscosity on the fluid flow. It has an important effect on the aerodynamic characteristic of the aircraft. The variable Reynolds number research of the high lift for one of the civil turboprop aircraft is completed by the commercial software CFX. The effect of Reynolds number on the lift coefficient, stall characteristic, and the velocity characteristic of the boundary layer are also analyzed in detail. The research indicates that the Reynolds number has the notable effect on the maximum lift coefficient and the stall angle. The state of the flow separation on the wing is changed obviously under the different Reynolds number. The area of the separation becomes smaller when the Reynolds number is increased. The state of the boundary layer is different under the different Reynolds number. When the Reynolds number increases, the velocity profile is fuller, and the trend of separation is limited.
turboprop aircraft; high lift; Reynolds number; aerodynamic characteristic
2016-07-11;
2016-10-09
航空科学基金(20143203002)
许瑞飞,xrf803@163.com
1674-8190(2016)04-420-06
V211
A
10.16615/j.cnki.1674-8190.2016.04.004
许瑞飞(1985-),男,硕士,高级工程师。主要研究方向:飞机气动力设计与计算。
钱瑞战(1966-),男,博士,研究员。主要研究方向:飞机气动力设计。
雷武涛(1975-),男,硕士,研究员。主要研究方向:飞机总体气动设计。
