初中数学几何教学证明中“基本图形”的作用分析

汪德

中图分类号：G633.6 文献标识码：B文章编号：1672-1578（2016）06-0244-01

在初中阶段，学习几何基本知识至关重要，要引导学生学习基本的几何定义、公理等，借助"基本图形"，逐渐培养学生逻辑思维能力、抽象思维能力等，提高他们分析、解决问题的能力，促进他们的全面发展。以此，改变初中数学教学现状，提高课堂教学效率与质量。

1.简化教师几何教学方法，拓展学生思维

在初中几何教学中，想要提高学生解题效率，缩短几何题证明时间，必须准确了解不同类型的几何图形，要引导学生把基本图形从复杂图形中分解出来，记住必要的基本图形性质，便能把复杂的图形简单化，降低题目难度。在初中几何教学中，"互为邻补角的两个角品分线互相垂直"这一结论是学生必须正确理解、掌握的。同时，在适当延伸、拓展基本图形的基础上，能够进一步拓展学生思维，也能在一定程度上简化教师的几何教学方法。在"基本图形"作用下，关于角平分线题目思路也会更加清新，解题过程更加简单，具有较好的化难为易的作用，学生也能准确理解、掌握新的知识点。

例如：∠AOB、∠BOC为邻补角，OD、OE为∠AOB、∠BOC的平分线，得出OD⊥OE。下面是相关的图形。

在角平分线教学中，教师可以借助该基本图形来简化相关的证明过程，迅速找到解题的突破口，提高解题速度与准确率。

例如：小东根据提示，画出了45度的角，即：需要先做出两条相互垂直的直线MN、PQ，点A、B是直线MN、PQ上的任意一点，需要作出∠ABP的平分线，即BD，并将其反向延长，和∠OAB平分线相交于点C，而∠C就是所求的45度角。请问是否正确，并进行证明。下面是相关的图形。

对于这道题来说，图形复杂化，题中的条件也非常零乱，但仔细审题，便能发现题目中的核心条件，即两条角平分线，这就是解题的关键所在。在解答该题的时候，学生可以根据相关定理的基本图形，适当简化图形，并借助图形变换，加入一些关键性图形，解题思路也更加清晰，迅速找到突破口，提高解题正确率。还能拓展学生的思维，做到举一反三，学以致用，不断培养他们的数学思维。

2.巧妙引入其他知识点，培养学生创新素养

例如：B是直线DF上的某点，∠ABC和Rt∠相等，以A、C两点为基点，做直线的垂线，D、E是对应垂足。那么，△ABD ∽△BCE，如果AB和BC相等，△ABD ≌△BCE。下面是相关的图形。

对于该图形来说，学生大都非常熟悉，分别在全等三角形、相似三角形中出现，只是没有两线段相等的相关条件。在反复练习中，大部分学生都能灵活应用该基本图形。在此基础上，教师需要根据学生掌握情况，把其他相关知识点巧妙地融入到该图形中，使其相互融合，引导学生进一步深入思考，为培养他们的创新思维做好铺垫。

例如：已知正三角形ABC的边长为8，其中BD为3，角ADF的度数为60度，请求出AE的长度。下面是相关的图形。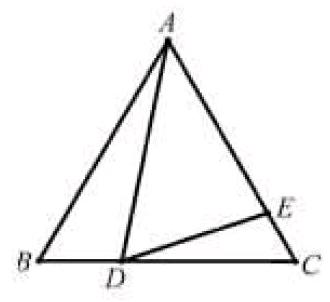

就该题来说，该图形是在基本图形基础上得出的，基本图形中的直角三角形已经变为等边三角形，也就是说将对应角从90度变为60度，其他条件都没有任何变化，和原题有着相同的解题思路。简单来说，学生只要掌握了基本图形的解题方法，便能迅速找到解答该题的突破口，正确解答该题。为此，在几何知识教学中，教师要让学生充分意识到基本图形的重要性，准确理解、掌握相关知识点，并巧妙地应用到各类变形题中，基本图形拓展题中，把知识学活，转化为自己的知识点。

3.结语

总而言之，在初中几何教学中，教师要对"基本图形"引起重视，要优化利用不同类型的"基本图形"，不断深入研究各类基本图形，结合初中生的兴趣爱好、个性特征、心理特征等，优化几何教学方法，巧妙地引入其他相关知识，和图形有机融合，不断拓展学生思维，引导他们积极思考，培养他们的创新素养，逐渐提高学生灵活运用各类基本图形有效解决对应的几何问题。以此，更好地发挥"基本图形"在初中几何课堂教学中所起的作用，提高课堂教学有效性。