高中数学函数极限证明的例题梳理

■江汉大学　冯　青



高中数学函数极限证明的例题梳理

■江汉大学冯青

函数是被广泛应用的数学概念，在自然科学、工程技术，甚至某些社会科学中都会认识到函数。研究高中数学函数不等式证明的方法是极限。无论是再中学数学还是在大学数学中，极限的概念和思想都非常重要，从量变中认识质变，都要用到极限。我们还能够通过极限研究函数的连续性、可导性、收敛性等概念。因此极限概念是研究函数的重要概念，具有一定的理论意义和现实意义。本文梳理了极限概念，归纳总结了部分求极限的方法，在进行不等式极限求解的过程中，巧妙地运用了高中数学中相关的理论知识，达到巩固、复习，培养学生一题多解的思维能力，并希望能把极限的思想运用到更广泛的领域。

一、辨析概念，夯实基础

极限思想作为研究函数最基本的方法，早在古代就有比较清楚的描述。中国魏晋时期杰出的数学家刘薇于公元263年创立了“割圆术”，就是使用了极限的思想。在近代数学许多分支中一些重要的概念与理论都是极限和连续函数概念的推广、延拓和深化。在19世纪，柯西根据微积分研究的需要改进了极限方法。近年许多专家学者对函数极限的计算方法作了研究，并取得了一定的突破。房俊、李广民研究了用中值定理求函数极限的方法；曹学锋、孙幸荣讨论了利用无穷小量计算函数的极限。极限思想在高中数学函数中的应用越来越大。

众所周知，常见的求极限的方法包含无穷小量、重要极限公式、洛必达法则等。但实际在求极限时并不是依靠单一方法，而是把多种方法加以综合运用。前人在对求函数极限的方法大多是单一的，没有一个对求函数极限的方法进行全面的归纳总结。对函数极限求解方法的讨论是本文的核心点，本文通过一些典型例题来讨论求函数极限的解法并加以综合运用。这就需要学生牢固地掌握求极限的方法并对函数极限的方法加以归纳、总结，希望对初学者有所帮助。

二、重点总结

笔者通过查阅资料总结出各种求函数极限的计算技巧，然后结合具体的例子给出这些计算技巧的具体应用，最后对内容进行整合。常见的求极限的方法有定义法、利用极限四则运算、利用夹逼性定理求极限、利用两个重要极限求极限、用洛必达法则、用定积分求极限、利用无穷小量性质和无穷小量与无穷小量之间的关系、利用变量替换等等方法求极限。此外，数学归纳法也是常见的方法之一。

（一）定义：（各种类型的极限的严格定义参见《高等数学》函授教材，这里不一一叙述）。

说明：（1）一些最简单的数列或函数的极限（极限值可以观察得到）都可以用上面的极限严格定义证明，例如：

（2）在后面求极限时，（1）中提到的简单极限作为已知结果直接运用，而不需再用极限严格定义证明。

（二）极限运算法则

定理1 已知limf（x），limg（x）都存在，极限值分别为A，B，则下面极限都存在，且有

（1）lim［f（x）±g（x）］=A±B

（2）limf（x）·g（x）=A·B

说明：极限号下面的极限过程是一致的；同时注意法则成立的条件，当条件不满足时，不能用。

（三）两个重要极限

说明：不仅要能够运用这两个重要极限本身，还应能够熟练运用它们的变形形式，

（四）等价无穷小

定理2 无穷小与有界函数的乘积仍然是无穷小（即极限是0）。

定理3 当x→0时，下列函数都是无穷小（即极限是0），且相互等价，即有：

X～sinx～tanx～arcsinx～arctanx～1n（1+x）～ex-1。

说明：当上面每个函数中的自变量x换成g（x）时（g（x）→0），仍有上面的等价关系成立，例如：

当x→0时，e3x-1～3x；1n（1-x2）～-x2。

定理4 如果函数f（x），g（x），f1（x），g1（x）都是x→x0时的无穷小，且f（x）～f1（x），g（x）～g1（x），则当存在时，也存在且等于，即

三、举例解析

极限在高中数学中的应用十分常见，本文现拟从以下几个例题来探讨求函数极限的方法。

（一）分类讨论求极限

例已知数列an｛｝bn｛｝、都是由正数组成的等比数列，公比分别为p，q，其中p＞q，且p≠1，q≠1，设cn=an=bn，Sn为数列Cn｛｝的前n项和，求

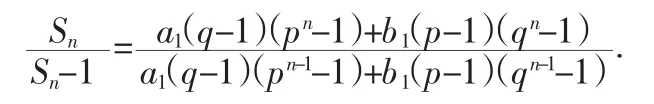
分两种情况讨论；

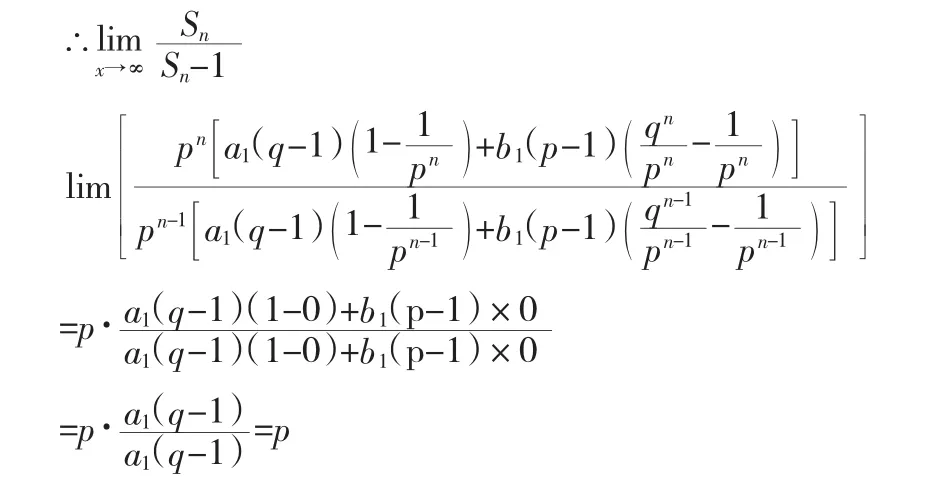
（2）当p＜1时，∵0＜q＜p＜1，

说明：先化简，再求极限是求极限经常用到的方法，该题考查了数列的基础知识、恒等变形的能力，分类讨论的数学思想方法和求极限的方法。

（二）自变量趋向无穷时函数的极限

例求下列极限：

分析：第（1）题中，当x→∞时，分子、分母都趋于无穷大，属于“”型，变形的一般方法是分子、分母同除以x的最高次幂，再应用极限的运算法则.

（三）无穷减无穷型极限求解

例求极限：

分析：含根式的函数求极限，一般要先进行变形，进行分子、分母有理化，再求极限。

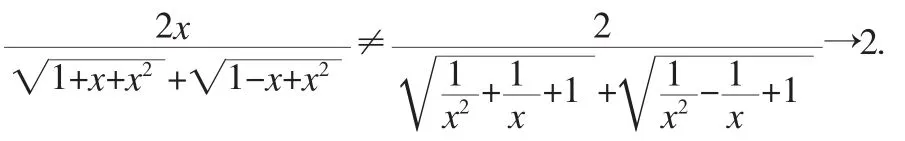
（四）利用运算法则求极限

例计算下列极限：

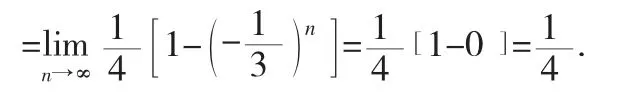
说明：该题计算时，要先求和，再求所得代数式的极限，不能将只适用有限个数列的加、减、乘、除的数列极限的四则运算法则，照搬到无限个数列的加、减、乘、除。

（五）用二项式定理展开或逆用等比数列和公式化简求极限

例设p∈N*，求

或：逆用等比数列求和公式：

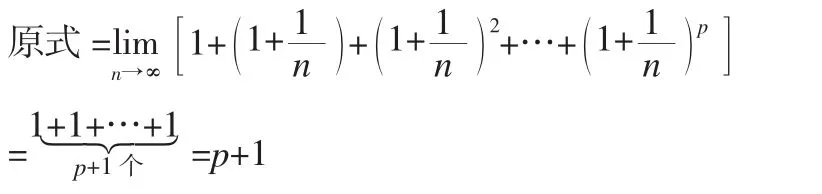
（六）零乘无穷型转化为无穷除无穷型

分析：当n→∞时，所求极限相当于0·∞型，需要设法化为我们熟悉的型.

说明：对于这种含有根号的0·∞型的极限，可采取分子有理化或分母有理化来实现.如本题是通过分子有理化，从而化为，即为型，也可以将分子、分母同除以n的最高次幂即，完成极限的计算.

（七）零比零型的极限

说明：本题采用的换元法是把x→0化为y-1→0，这是一种变量代换.灵活地运用这种代换，可以解决一些型的极限问题.

（八）利用数学归纳法求极限

归纳法包含不完全归纳法和完全归纳法。

①不完全归纳法：根据事物的部分（而不是全部）特殊事例得出一般结论的推理方法。

②完全归纳法：根据事物的所有特殊事例得出一般结论的推理方法。

数学归纳法常与不完全归纳法结合起来使用，用不完全归纳法发现规律，用数学归纳法证明结论。

例若数列｛an｝的通项an=2n-1，设数列｛bn｝的通项bn=1+，又记Tn是数列｛bn｝的前n项的积.

（Ⅰ）求T1，T2，T3的值；

（Ⅱ）试比较Tn与的大小，并证明你的结论.

分析与证明：

（1）∵an=2n-1

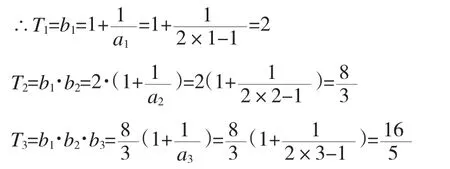
假设n=k（k≥1）时，原不等式成立，即

当n=k+1时，不等式左边为

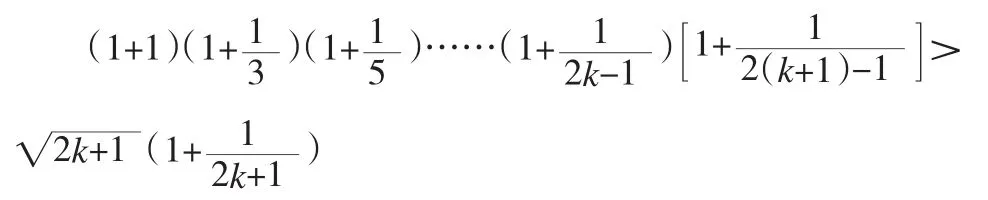
即n=k+1时不等式也成立，∴对于n∈N，则有

说明：数学归纳法步骤如下

①验证当取第一个时结论成立；

②由假设当（）时，结论成立，证明当时，结论成立；

根据①②对一切自然数时，都成立。

四、总结

在学习数学的过程中，敢于探索，善于总结，是我们学习数学必须具备的素质。本文只是举例说明了在极限中证明中常用的几种方法的运用，另外还有很多其它方法可以灵活综合的解决问题，这需要我们平时多观察和总结。同时，我们需要在解题时能举一反三，从概念出发深入分析极限与函数在数学中的应用。

极限是数学中不可缺少的工具之一，它在解决一些数学问题中具体所体现出来的作用值得我们去思考，掌握好这个工具，对学好这门内容抽象逻辑性强的高等数学具有一定的帮助。

责任编辑郑占怡