基于稀疏拉伸式COLD传感器的波达角和极化参数估计

赵继超　陶海红　高志奇

(西安电子科技大学 雷达信号处理国家重点实验室,西安 710071)



基于稀疏拉伸式COLD传感器的波达角和极化参数估计

赵继超陶海红高志奇

(西安电子科技大学 雷达信号处理国家重点实验室,西安 710071)

摘要同点正交配置磁环和电偶极子(Co-centered Orthogonal Loop and Dipole, COLD)是常用的二分量电磁矢量传感器之一,但是COLD传感器没有充分利用磁环和电偶极子分量的空间信息. 针对由COLD传感器组成的均匀线阵,磁环分量保持不变,将电偶极子分量沿正交方向稀疏拉伸,形成L形阵,扩展阵列的空间孔径,提出了基于广义旋转不变的降维多重信号分类算法. 该算法利用L形阵的几何构形,将导向矢量分隔成三部分,利用广义旋转不变矩阵分别估计各个部分,使得波达角和极化参数仅需一维谱峰搜索就可以估计得到. 同时,在参考点处新增一个电偶极子天线,利用四元数模型解决了由于稀疏拉伸引起的相位周期模糊问题. 仿真实验验证了所提算法的有效性.

关键词同点配置正交磁环-电偶极子;波达角;极化;基于广义旋转不变的降维多重信号分类算法

引言

由电磁矢量传感器(Electromagnetic Vector Sensor, EMVS)组成的极化敏感阵列是一种新型阵列,与传统标量阵列相比,不仅能够利用阵元的空间分布获取信号的空域信息,而且还可以获取信号的极化状态,使得极化敏感阵列在空间源定位上有更高的分辨能力和更强的抗干扰能力.

Paldi. N. E.基于麦克斯韦方程于1994年在文献[1]中推导出复数模型下的极化敏感阵列的数学模型,奠定了极化敏感阵列信号处理的基础. K.T.Wang、袁鑫等学者在文献[2-5]阐述了如何利用单个六分量EMVS或者单个三分量EMVS去估计正弦信号的波达角(Direction of Arrival, DOA)和极化参数,但是单个EMVS的孔径信息非常有限,参数估计精度较低,且这类算法只适用于正弦信号,算法实际应用很受限.

为了获取更高的参数估计精度,由二分量EMVS组成的二维极化敏感阵列引起了国内外诸多学者的广泛研究. 二维极化敏感阵列,由于其天线结构简单,很容易将标量阵中的一些算法扩展到极化敏感阵列中. 如文献[6]针对由同点正交配置磁环-电偶极子(Co-centered Orthogonal Loop and Dipole, COLD)组成的均匀线阵(Uniform Linear Array, ULA),将空间旋转不变参数估计[7](Estimation of Signal Parameters via Rotational Invariance Techniques, ESPRIT) 算法拓展到了极化域,文献[8]将多重信号分类方法[9](Multiple Signal Classification Method, MUSIC)应用到二维极化敏感阵列中.

极化敏感阵列中的算法不单单是标量阵列算法的扩展,由于极化敏感阵列自身的特性,也有一些只适用于极化敏感阵列的算法. 如文献[10-11]针对循环平稳信号,研究了基于极化敏感阵列的空域/极化域的数据平滑解相干算法,与空间平滑相比,极化平滑对阵列排布没有特殊要求,且不损失孔径信息. 文献[12]针对二维极化敏感阵列引入了四元数模型,提出了四元数MUSIC (Quaternion Multiple Signal Classification Method, Q-MUSIC)算法,但是算法需要四维谱峰搜索. 文献[13]改进了Q-MUSIC算法,并提出了降维四元数ESPRIT(Dimension Reduction Quaternion Estimation of Signal Parameters via Rotational Invariance Techniques, DRQ-ESPRIT),该算法有效降低了算法复杂度,使得DOA和极化参数无需谱峰搜索就可以估计得到.

但是,这些算法均采用的是传统二分量EMVS,传感器分量是空间共点配置,没有充分利用其空间信息. 为了充分利用各传感器分量的空间信息,本文针对由COLD传感器组成的ULA,保持磁环分量不变,将电偶极子分量沿正交方向均匀稀疏拉伸,形成L形阵,并提出了基于广义旋转不变的降维多重信号分类算法(Generalized Rotational Invariance Based Dimension Reduction Multiple Signal Classification Method, GRIDR-MUSIC). 所提算法利用L形阵的几何构形,将导向矢量分隔成三部分,利用广义旋转不变矩阵仅需一维谱峰搜索就可以估计得到DOA和极化参数. 此外,在参考点新增一个电偶极子,利用四元数模型解决了由于稀疏拉伸引起的相位周期模糊问题.

本文结构如下:第一部分给出了基于拉伸式COLD传感器的极化敏感阵列的数学模型,第二部分详细讲述了所提算法,第三部分给出了算法运算复杂度对比,第四部分用仿真实验对算法性能进行说明,第五部分总结全文.

符号定义: (·)†,(·)-1,(·)H和(·)*分别表示广义逆,矩阵求逆,共轭转置和共轭运算; arg(·)表示取角度运算;E[·]表示数学期望. R表示有理数集,[·]r,[·]i,[·]j和[·]k分别表示取四元数的实部,第一虚部(i部),第二虚部(j部)和第三虚部(k部).

1数学模型

假设沿z轴分布的ULA由M个COLD传感器组成,其中,磁环平行于x-y平面,电偶极子严格指向z轴,阵元间距d1为半波长,如图1所示.

为了充分利用COLD传感器中电偶极子和磁环分量的空间信息,本文保持沿z轴均匀分布的磁环不变,将电偶极子沿y轴均匀拉伸,为了弥补类空间平滑造成的阵列孔径损失,电偶极子间的拉伸间距d2大于半波长. 阵元间距大于半波长会引起相位周期模糊问题,为此本文在参考点新增一个严格指向x轴的电偶极子,利用四元数模型来解相位周期模糊. 经过拉伸处理后的阵列如图2所示.

图1　COLD传感器组成的ULA

图2　拉伸式COLD传感器组成的L形阵

记由沿z轴分布,平行于x-y平面的磁环组成的ULA为子阵1,由沿y轴分布,严格指向z轴的电偶极子组成的ULA为子阵2. 假设有N个彼此独立的远场窄带完全极化信号入射到该阵,则子阵1,子阵2和新增严格指向x轴的电偶极子的接收数据矩阵可以分别表示为:

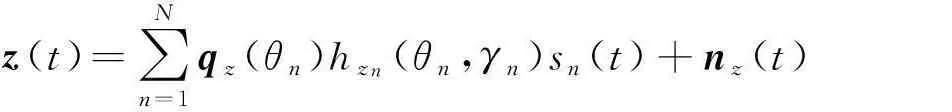
z(t) =∑Nn=1qz(θn)hzn(θn,γn)sn(t)+nz(t)

=Az(θ,γ)s(t)+nz(t),

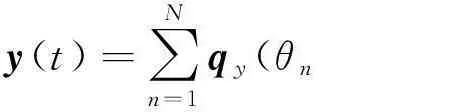
(1)

,φn)ezn(θn,γn,ηn)sn(t)+ny(t)

=Ay(θ,φ,γ,η)s(t)+ny(t),

(2)

(3)

式中: Az=[az(θ1,γ1),…,az(θN,γN)]为子阵1的阵列流形; az(θn,γn)=qz(θn)hzn(θn,γn)为第n个信号的导向矢量,n=1,2,…,N; qz(θn)=[1,e-j2πd1cosθn/λ,…,e-j2π(M-1)d1cosθn/λ]T表示阵元空间相移矢量;极化-角度域导向矢量hzn=sinθncosγn为沿z轴的磁场表达式,阵元间距d1=λ/2,λ是波长,φn∈[0,2π),θn∈[0,π],γn∈[0,π/2],ηn=[-π,π)分别是第n个信号的方位角、俯仰角、极化辅角和极化相位差. Ay=[ay(θ1,φ1,γ1,η1),…,ay(θN,φN,γN,ηN)]为子阵2的阵列流形,ay(θn,φn,γn,ηn)=qy(θn,φn)ezn(θn,γn,ηn)为第n个信号的导向矢量,qy(θn,φn)=[1,e-j2πd2sinθnsinφn/λ,…,e-j2π(M-1)d2sinθnsinφn/λ]T表示阵元空间相移矢量,阵元间距d2大于半波长,极化-角度域导向矢量ezn=-sinθnsinγnejηn为沿z轴的电场表达式. 极化-角度域导向矢量exn=cosφncosθnsinγnejηn-sinφncosγn为沿x轴的电场表达式. s(t)=[s1(t),…,sN(t)]T为信号矢量,nx(t),ny(t)和nz(t)均为加性高斯白噪声,并假设矢量传感器接收的每个噪声分量彼此独立且功率为σ2.

为了方便讨论,令

αn=-2πd1cosθn/λ,

(4)

βn=-2πd2sinθnsinφn/λ.

(5)

则qz(θn)和qy(θn,φn)分别由qz(αn)和qy(βn)表示:

qz(αn)=[1,ejαn,ej2αn,…,ej(M-1)αn]T,

(6)

qy(βn)=[1,ejβn,ej2βn,…,ej(M-1)βn]T.

(7)

定义第n个信号的正交相位差Δn为

Δn=βn-αn.

(8)

本文需要做以下三点的假设: 1)αa-βa≠αb-βb+2πg,g为整数,a,b∈{1,2,…,N}; 2) 入射源个数已知; 3) 俯仰角不等于0和π,极化辅角不等于0和π/2.

2GRIDR-MUSIC算法

2.1传统四维谱峰搜索的参数估计

拉伸式COLD传感器组成的L形阵列的接收数据矩阵可以表示为

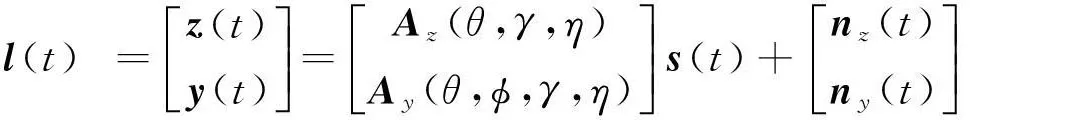
l(t) =z(t)y(t)éëêêùûúú=Az(θ,γ,η)Ay(θ,ϕ,γ,η)éëêêùûúús(t)+nz(t)ny(t)éëêêùûúú

=A(θ,φ,γ,η)s(t)+n(t).

(9)

式中,A=[a(θ1,φ1,γ1,η1),…,a(θN,φN,γN,ηN)]为L形阵的阵列流形,第n个信号的导向矢量可以表示为

(10)

接收数据的协方差矩阵为:

Rll=E[l(t)lH(t)]=ARsAH+σ2I2M.

(11)

式中,Rs是信号矢量协方差矩阵,因为假设信号为彼此独立的远场窄带完全极化信号,所以Rs为实对角矩阵,即Rs=diag{ps1,ps2,…,psN},对角线元素表征了入射信号的功率,I2M为2M维单位矩阵.

对Rll进行特征值分解,噪声子空间Un为由2M-N个小特征值对应的特征向量组成的矩阵,信号子空间Us为由N个大特征值对应的特征向量组成的矩阵.

由传统MUSIC算法可知,DOA和极化参数可以通过下式进行四维谱峰搜索估计得出:

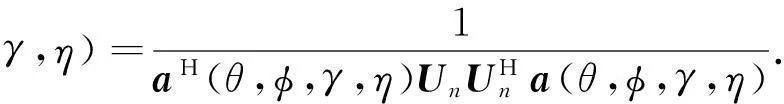
(12)

四维谱峰搜索的运算量巨大,且由于d2大于半波长会引起相位周期模糊,使得式(12)估计得到的参数不唯一. 所以本文提出了GRIDR-MUSIC算法,所提算法利用L形阵的几何构形,将导向矢量a(θ,φ,γ,η)分隔成三部分,并通过子阵1和子阵2的广义旋转不变性,仅需一维谱峰搜索就可以估计得到DOA和极化参数,有效地降低了运算量. 同时利用新增严格指向x轴的电偶极子的接收数据x(t),基于四元数模型解决了相位周期模糊问题.

2.2将导向矢量分隔为三部分

基于子空间理论可知信号子空间Us与阵列流形A张成的空间一样,即

(13)

式中,T为N×N维满秩矩阵. Az和Ay具有广义旋转不变的结构[14],可以表示为

Ay=[ay(θ1,φ1,γ1,η1),…,ay(θN,φN,γN,ηN)]

=[Ψ1az(θ1,γ1),…,ΨNaz(θN,γN)].

(14)

其中广义旋转不变矩阵Ψn可以表示为

Ψn(Δn,γn,ηn)=diag{-tanγnejηn,-tanγnejηnejΔn,

…,-tanγnejηnej(M-1)Δn}.

(15)

因此,导向矢量a(θ,φ,γ,η)可以重新表示为

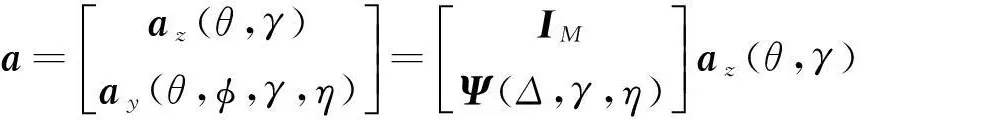
a =az(θ,γ)ay(θ,ϕ,γ,η)éëêêùûúú=IMΨ(Δ,γ,η)éëêêùûúúaz(θ,γ)

=Γ(Δ,γ,η)qz(α)hz(θ,γ).

(16)

记Γ(Δ,γ,η)为导向矢量的第一部分,qz(α)为导向矢量的第二部分,hz(θ,γ)为导向矢量的第三部分.

2.3估计导向矢量的第一部分

传统广义旋转不变子空算法(Generalized Estimation of Signal Parameters via Rotational Invariance Techniques, G-ESPRIT)[14]指出,Ψ通过对下式函数进行三维谱峰搜索估计得到:

f(Δ,γ,η)=

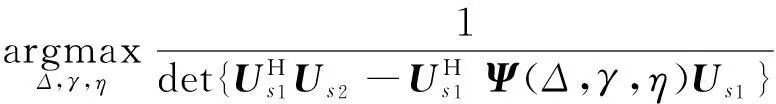
(17)

但是,三维谱峰搜索的运算量仍然十分巨大,因此本文利用子阵1和子阵2互相关矩阵的对角线元素来对式(17)降维处理,以损失N个传感器的孔径自由度为代价,仅通过一维谱峰搜索就可以估计出Ψ中的Δ,γ和η.

2.3.1估计参数Δ

子阵1和子阵2接收数据的互相关矩阵可以表示为:

Rzy=E[y(t)zH(t)]=AyRsAz

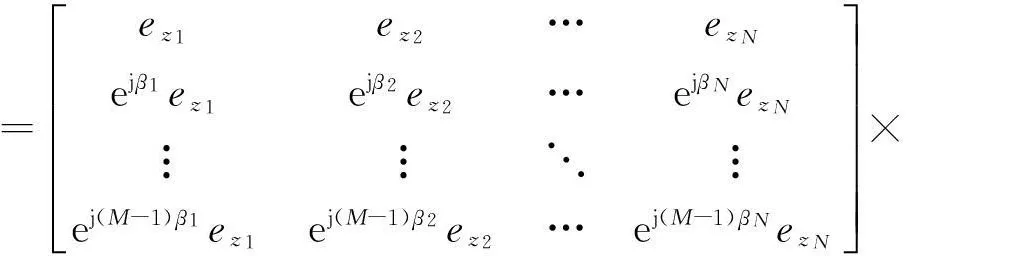
= ez1ez2…ezNejβ1ez1ejβ2ez2…ejβNezN︙︙⋱︙ej(M-1)β1ez1ej(M-1)β2ez2…ej(M-1)βNezNéëêêêêêêùûúúúúúú×

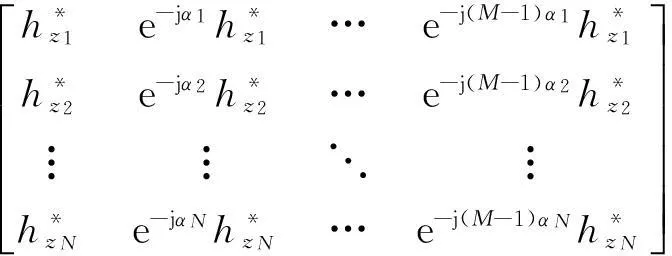
(18)

记rdiag为互相关矩阵Rzy对角线元素,rdiag可以表示成:

rdiag=

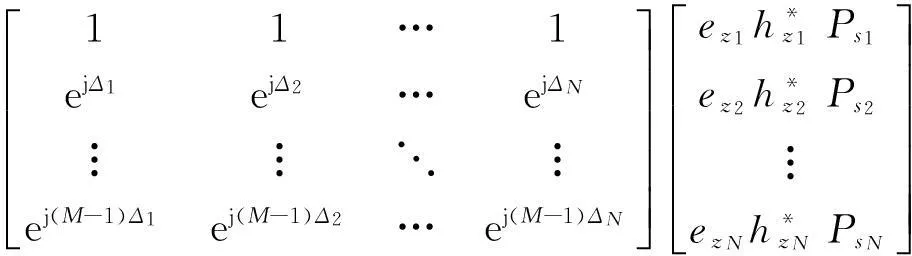
(19)

本文假设信源数已知,类似于参考文献[15]的类空间平滑处理,构造(M-N+1)×N维矩阵Rdiag:

Rdiag=[r1,r2,…,rN].

(20)

式中,rn=rdiag(n∶M-N+n),n=1,2,…,N,rdiag(p:q)表示由rdiag的第p行到第q行组成的列矢量. Rdiag可以表示为三个矩阵相乘的形式:

Rdiag=UVW.

(21)

其中,

(22)

(23)

(24)

定义选择矩阵J1=[IM-N,01],J2=[01,IM-N],其中,IM-N是(M-N)×(M-N)维单位矩阵,01是(M-N)×1的全零列向量,构造旋转不变结构:

J2Rdiag=J2UVW=J1UΩVW

=J1Rdiag(VW)-1ΩVW.

(25)

式中,旋转矩阵Ω为

Ω=diag{ejΔ1,ejΔ2,…,ejΔN}.

(26)

旋转矩阵Ω可以通过特征值分解矩阵(J1Rdiag)†J2Rdiag得到的特征值进行估计,记为

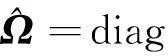
(27)

2.3.2估计极化参数

(28)

(29)

基于式(21),矩阵V可以通过下式估计得出:

(30)

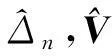
(31)

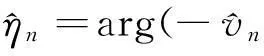
(32)

(33)

明显看出,式(33)仅需N次一维谱峰搜索就可以估计出入射信号的极化辅角,与式(17)相比,有效地降低了运算量,不足之处就是在利用类空间平滑处理构造Rdiag时,损失了N个传感器的孔径自由度,本文将电偶极子沿y轴稀疏拉伸就是为了弥补孔径自由度损失引起的参数估计精度降低. 但是本文算法依然存在可估计信源个数降低N个的不足.

2.4估计导向矢量的第二部分

利用MUSIC算法通过式(12)估计参数时,谱峰的形成仅仅取决于导向矢量的第一部分和第二部分,这是因为导向矢量的第三部分hz(θ,γ)=sinθncosγn不会影响导向矢量a和噪声子空间Un的正交性,hz(θ,γ)类似于窗函数,只会影响谱峰的高低,所以导向矢量a可以简化成:

(34)

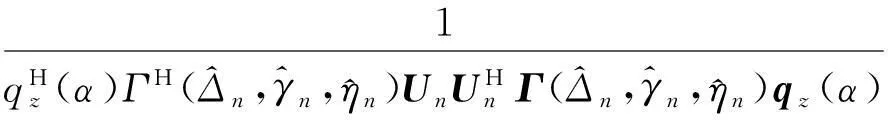
(35)

(36)

基于式(8)可得:

(37)

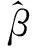
2.5利用四元数模型解相位周期模糊

2.5.1四元数定义

四元数[16]是由Hamilton于1843提出的一种四维超复数,四元数h由一个实部和三个虚部组成:h=a+bi+cj+dk,其中a,b,c,d∈R,虚部i, j, k满足:

i2=j2=k2=ijk=-1;

ij=-ji=k; ki=-ik=j;jk=-kj=i.

简要介绍下本文用到的四元数基本运算,定义四元数h的共轭h*为h*=a-bi-cj-dk.

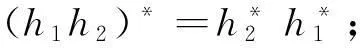
2.5.2解相位周期模糊

在图2中参考点处,平行于x-y平面的磁环和新增严格指向z轴的电偶极子的接收数据可以用四元数联合表示为:

x0(t)=

n0(t).

(38)

式中,四元数表示的极化-角度域导向矢量Ψn可以表示为:

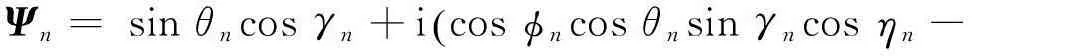
Ψn= sinθncosγn+icosϕncosθnsinγncosηn-(

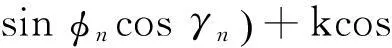
(39)

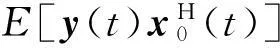
=MG.

(40)

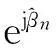
(41)

所以可以得到G:

(42)

记G(n)为G的第n个元素,可以表示为:

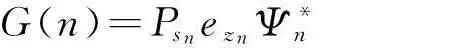
G(n) =PsneznΨ*n

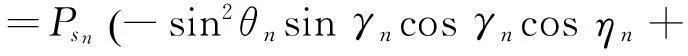
=Psn-sin2θnsinγncosγncosηn+(

jsin2θnsinγncosγnsinηn+

(43)

利用G(n)的第二虚部(j部)和第三虚部(k部),第n个信号的方位角可以粗估为:

(44)

(45)

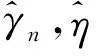
2.6GRIDR-MUSIC算法流程

本文所提GRIGR-MUSIC算法仅需要一维谱峰搜索就可以估计入射信号的DOA和极化参数,且无需参数匹配,算法流程可以归结如下:

1) 特征值分解L阵接收数据的协方差矩阵得到信号子空间Us和噪声子空间Un;

2) 利用L阵的几何构形,将导向矢量分隔成三部分,如式(16)所示;

3) 基于子阵1和子阵2的广义旋转不变结构,通过式(27)估计出导向矢量第一部分的正交相位差Δ,并利用式(32)和(33)估计极化相位差η和极化辅角γ;

5) 利用四元数模型,通过式(43)先粗估出方位角,然后基于最小二乘法,利用方位角的粗估值去解式(37)的相位周期模糊,从而精确地估计出方位角.

3计算量比较

两个实数相加计1次加法,相乘计1次乘法,则两个复数相加算2次加法,相乘算2次加法和4次乘法;复数和四元数相加算2次加法,相乘算4次加法和8次乘法;两个四元数相加算4次加法,相乘算12次加法和16次乘法.此节将本文算法与文献[8]的MUSIC算法和文献[14]中的G-ESPRIT算法在运算量方面进行了对比,由于本文算法,MUSIC算法和G-ESPRIT算法的运算量主要集中在特征值分解,矩阵求逆和谱峰搜索,且乘法运算的资源耗费是加法的4～6倍,因此本文只分析上述三种运算的乘法运算量.

表1　三种算法的计算量

参数搜索范围设定如下:方位角θ∈[0,π],俯仰角φ∈[0,2π),极化辅角γ∈[0,π/2],极化相位差η∈[-π,π),搜索步长均匀为1/L弧度,N和M分别代表信源数和COLD传感器数,表1给出了三种算法的运算量.

由表1可以看出:传统MUSIC算法需要搜索数次的数量级为L4,G-ESPRIT算法的搜索次数的数量级为L3,而本文所提算法的搜索次数的数量级降低为L,且每次搜索的运算量也低于MUSIC算法和G-ESPRIT算法,虽然在矩阵求逆和特征值分解操作中运算量稍微有所增加,但是远小于谱峰搜索降低的运算量,所以本文算法在运算量方面明显小于传统的两种算法.

4仿真实验

在仿真实验部分给出了一些仿真结果来说明所提算法的性能,并与文献[6]所提的基于极化域ESPRIT算法和文献[13]所提的DRQ-ESPRIT算法进行了对比. 假设COLD传感器数目为6,入射信源数为2,信号的俯仰角、方位角、极化辅角和极化相位差分别为θ1=85°,φ1=76°,γ1=45°,η1=56°,θ2=62°,φ2=39°,γ2=27°,η2=33°,阵间距d1=λ/2,d2=2λ,蒙特卡洛实验次数为100.

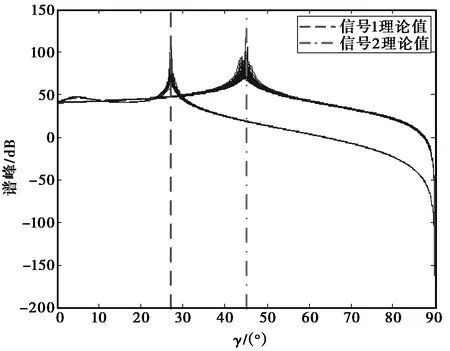
(a) 信噪比为5 dB,快拍数为200

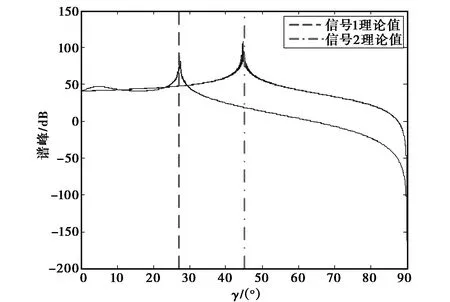
(b) 信噪比为20 dB,快拍数为200图3　对极化辅角降维搜索谱峰的结果

图3(a)和(b)分别为在5dB信噪比和20dB信噪比两种条件下,极化辅角的谱峰搜索图,搜索步长为0.1°.可以看出本文所提算法均在理论值处形成谱峰,且100次试验谱峰位置与理论值均基本吻合,说明通过子阵1和子阵2互相关矩阵的对角线元素来估计导向矢量第一部分是正确有效的.

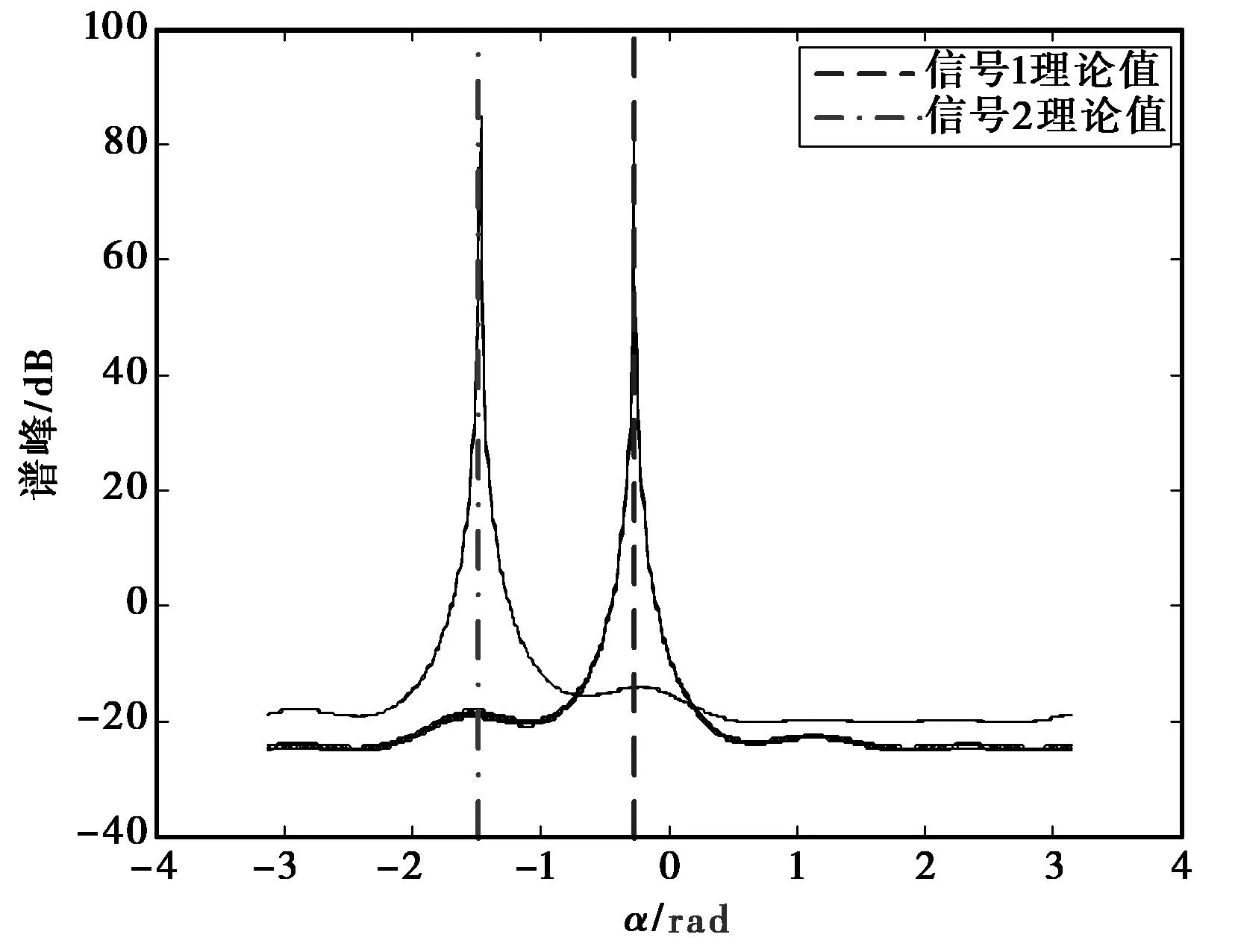
(a) 信噪比为5 dB,快拍数为200

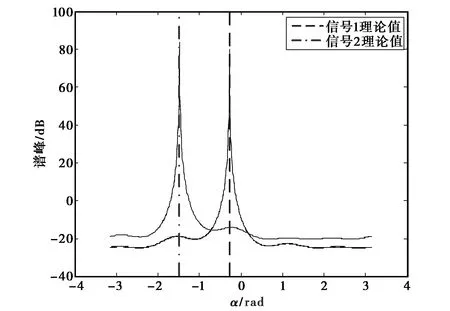
(b) 信噪比为25 dB,快拍数为200图4　对α降维谱峰搜索的结果

图4(a)和(b)分别为在低信噪比和高信噪比两种条件下,本文所提的GRIDR-MUSIC算法在估计α时的谱峰搜索图,搜索步长为0.01rad,可以看到无论是在低信噪比条件下还是在高信噪比条件下,形成谱峰位置与理论值基本吻合,说明所提算法估计得到的导向矢量的第二部分是正确有效的.

由传统的COLD传感器组成的ULA,利用文献[6]中的基于极化域ESPRIT算法,只能估计出入射信号的俯仰角,极化辅角和极化相位差,然而利用本文的基于拉伸式COLD传感器的GRIDR-MUSIC算法,可以将入射信号的DOA和极化参数全部估计,图5(a)和(b)为利用本文算法估计得到的方位角和俯仰角散布图,直观地可以看出通过本文算法估计得到的DOA参数抖动范围很小,估计精度高.

图6给出了利用本文算法和文献[13]中的算法估计DOA和极化参数,标准误差随信噪比的变化曲线,快拍数设为200.本文算法和文献[13]中的算法均需要经过类空间平滑处理,均损失了N个传感器的自由度,但是由于将电偶极子沿正交方向稀疏拉伸,扩展了原来的极化敏感阵列的空间孔径,从而使得估计精度比文献[13]更高.

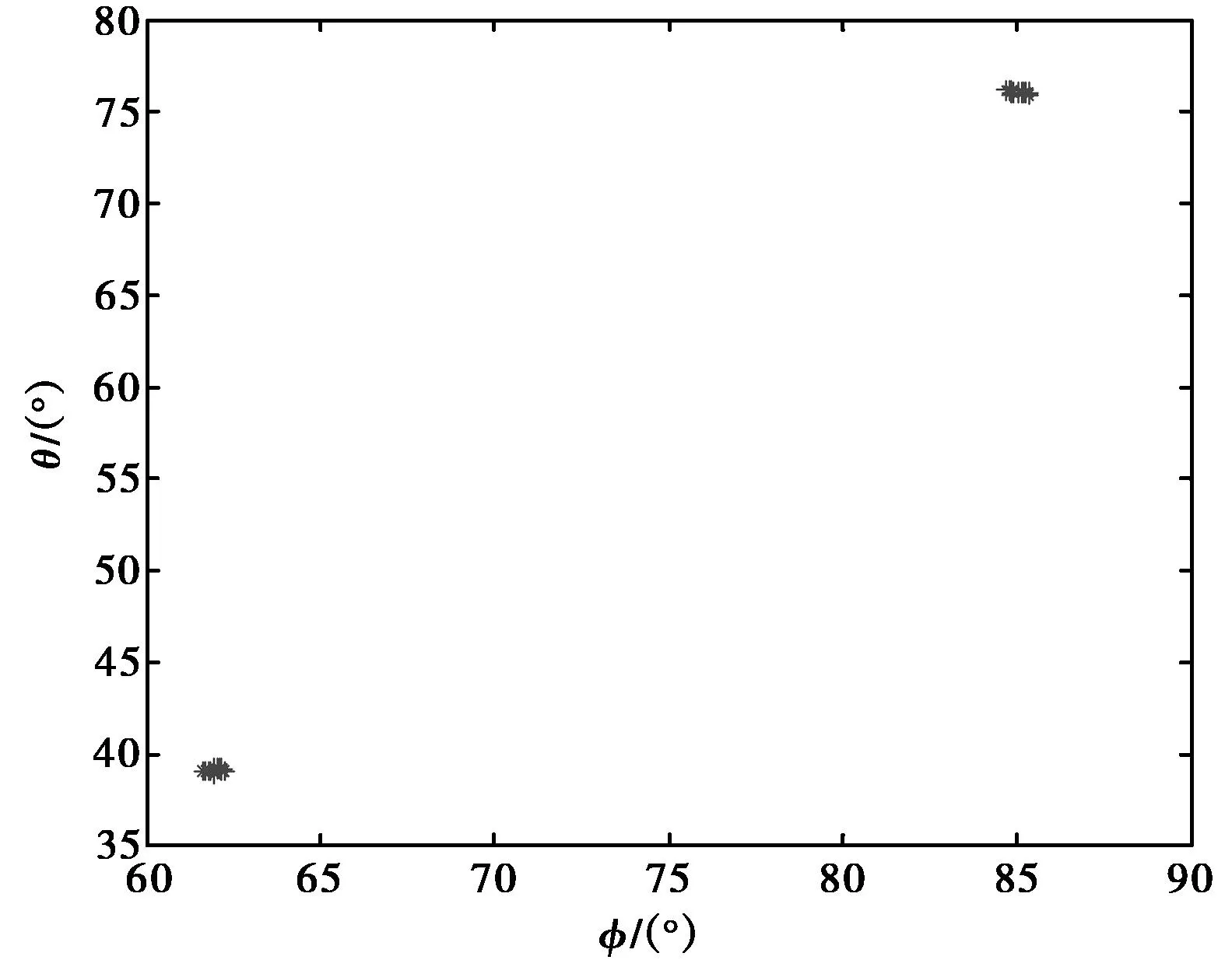
(a) 信噪比为5 dB,快拍数为200

(b) 信噪比为25 dB,快拍数为200图5　方位角和俯仰角估计散布图

图6　估计标准差随信噪比的变化曲线

5结论

传统COLD传感器因为电偶极子和磁环是空间同点配置,没有充分利用电偶极子和磁环分量的孔径信息,本文针对由COLD传感器组成的ULA,磁环分量保持不变,将电偶极子沿正交方向均匀稀疏拉伸,在没有增加传感器数量的基础上,原ULA被拉伸成L形阵,扩展了阵列的孔径信息,并基于拉伸后形成的L形阵,提出了GRIDR-MUSIC算法,所提算法将导向矢量分隔成三部分,并利用广义旋转不变矩阵分别估计各个部分,使得DOA和极化参数仅需一维谱峰搜索就可以估计得到,无需参数匹配. 最后,利用参考点新增电偶极子的接收数据构建四元数模型,解决了由于稀疏拉伸引起的相位周期模糊问题.

参考文献

[1]PALDINE.Vector-sensorarrayprocessingforelectromagneticsourcelocalization[J].IEEEtransactionsonsignalprocessing, 1994, 42(2): 376-398.

[2]WONGKT,ZOLTOWSKIMD.Uni-vector-sensorESPRITformultisourceazimuth,elevation,andpolarizationestimation[J].IEEEtransactionsonantennasandpropagation, 1997, 45(10): 1467-1474.

[3]WONGKT,YUANX.Vectorcross-productdirection-findingwithanelectromagneticvector-sensorofsixorthogonallyorientedbutspatiallynoncollocatingdipoles/loops[J].IEEEtransactionsonsignalprocessing, 2011, 59(1): 160-171.

[4]YUANX,WONGKT,XUZX,etal.Variouscompositionstoformatriadofcollocateddipoles/loops,fordirectionfindingandpolarizationestimation[J].IEEEsensorsjournal, 2012, 12(6): 1763-1771.

[5]YUANX.EstimatingtheDOAandthepolarizationofapolynomial-phasesignalusingasinglepolarizedvector-sensor[J].IEEEtransactionsonsignalprocessing, 2012, 60(3): 1270-1282.

[6]LIJ,STOICAP,ZHENGDM.EfficientdirectionandpolarizationestimationwithaCOLDarray[J].IEEEtransactionsonantennasandpropagation, 1996, 44(4): 539-547.

[7]ROYR,KAILATHT.ESPRIT—estimationofsignalparametersviarotationalinvariancetechniques[J].IEEEtransactionsonacoustics,speech,andsignalprocessing, 1989, 37(7): 984-995.

[8]MIRONS,BIHANNL,MARSJI.Quaternion-MUSICforvector-sensorarrayprocessing[J].IEEEtransactionsonsignalprocessing, 2006, 54(4): 1218-1229.

[9]SCHMIDTRO.Multipleemitterlocationandsignalparameterestimation[J].IEEEtransactionsonantennasandpropagation, 1986, 34(3): 276-280.

[10]RAHAMIMD,SHAVITR,TABRIKIANJ.Coherentsourcelocalizationusingvectorsensorarrays[C]//ProceedingsoftheIEEEInternationalConferenceonAcoustics,Speech,andSignalProcessing,HongKong, 2003: 141-144.

[11]SHIHY,HUH,SHIYW.Novelsolutionofdirectionfindingandpolarizationestimationofmultipathcyclostationarysignals[C]//Proceedingsofthe2ndInternationalConferenceonInnovationComputing,Informationandcontrol.Kumamoto,Japan, 2007.

[12]MIRONS,LEBIHANN,MARSJI.Quaternion-MUSICforvector-sensorarrayprocessing[J].Transactionsonsignalprocessing, 2006, 54(4): 1218-1229.

[13]赵继超, 陶海红, 高志奇.基于降维四元旋转不变子空间算法的波达角估计[J]. 电波科学学报, 2015, 30(3):483-490.

ZHAOJC,TAOHL,GAOZQ.DOAestimationusingdimensionreductionquaternionestimationofsignalparametersviarotationalinvariancetechniques[J].Chinesejournalofradioscience, 2015, 30(3): 483-490.(inChinese)

[14]GAOFF,GERSHMANAB.AgeneralizedESPRITapproachtodirectionofarrivalestimation[J].IEEEsignalprocessingletters, 2005, 12(3): 254-257.

[15]NIEX,LILP.Acomputationallyefficientsubspacealgorithmfor2-DDOAestimationwithL-shapedarray[J].IEEEsignalprocessingletters, 2014, 21(8): 971-974.

[16]HAMILTONWR.Onquaternions[J/OL].ProceedingoftheRoyalIrishAcademy, 1843, 3: 1-16. 1999[2015-06-17].http://www.emis.ams.org/classics/Hamilton/Quatern2.pdf.

Joint DOA and polarization parameters estimation based on sparsely stretched COLD sensors

ZHAO JichaoTAO HaihongGAO Zhiqi

(NationalLaboratoryofRadarSignalProcessing,XidianUniversity,Xi’an710071,China)

AbstractThe co-centered orthogonal loop and dipole (COLD) sensor is one of the most widely used two-component electromagnetic vector sensors. However, the COLD sensor does not make full use of the two component spatial aperture. The uniform linear array, which consists of COLD sensors, is considered. In order to extend the spatial aperture, all loop-components maintain the same, and all dipole-components are sparsely uniformly stretched along the orthogonal direction, thus an L-shaped array is formed. A generalized rotational invariance based dimension reduction multiple signal classification method (GRIDR-MUSIC) is proposed. The proposed algorithm uses the L-shaped array geometry to separate the steering vector into three parts, and uses the generalized rotational invariance matrix to estimate each part separately, thus direction of arrival (DOA) and polarization parameters can be estimated by only one-dimensional spectral peak search. In addition, a dipole is added in the conference point, and the quaternion model is used to resolve the phase cyclic ambiguity caused by sparsely stretching operation. Finally, the numerical simulations show the effectiveness of the proposed algorithm.

KeywordsCOLD sensor; DOA; polarization; GRIDR-MUSIC

收稿日期：2015-06-17

中图分类号TN958.93

文献标志码A

文章编号1005-0388(2016)02-0269-09

DOI10.13443/j.cjors.2015061701

作者简介

赵继超(1989-),男,陕西人,博士研究生,研究方向为极化敏感阵列参数估计.

陶海红(1976-),女,安徽人,西安电子科技大学电子工程学院教授,博士,博士生导师,研究方向为雷达信号处理与检测、高速实时信号处理、阵列信号处理.

高志奇(1980-),男,内蒙古人,博士研究生,研究方向为阵列信号处理.

赵继超, 陶海红, 高志奇. 基于稀疏拉伸式COLD传感器的波达角和极化参数估计[J]. 电波科学学报,2016,31(2):269-277. DOI: 10.13443/j.cjors.2015061701

ZHAO J C, TAO H H, GAO Z Q. Joint DOA and polarization parameters estimation based on sparsely stretched COLD sensors[J]. Chinese journal of radio science,2016,31(2):269-277. (in Chinese). DOI: 10.13443/j.cjors.2015061701

资助项目: 国家重点基础研究发展计划(973计划)(2011CB707001)； 国家自然科学基金(60971108)； 西安电子科技大学基本科研业务费资助项目(BDY061428)

联系人： 赵继超 E-mail: 13891894124@139.com