双基地分布式阵列MIMO雷达的DOA和DOD估计方法

马严　陈伯孝

(西安电子科技大学 雷达信号处理国家重点实验室,西安710071)



双基地分布式阵列MIMO雷达的DOA和DOD估计方法

马严陈伯孝

(西安电子科技大学 雷达信号处理国家重点实验室,西安710071)

摘要结合分布式阵列和双基地多输入多输出(Multiple-Input Multiple-Output, MIMO)雷达的特点,提出了一种新的双基地分布式阵列MIMO雷达的接收角(Direction of Arrival, DOA)和发射角(Direction of Departure, DOD)估计方法. 根据发射阵列和接收阵列的空域旋转不变特性,利用旋转不变估计技术(Estimation of Signal Parameters via Rotational Invariance Techniques,ESPRIT)获取无模糊DOA粗估计和高精度周期性模糊的DOA、DOD精估计;再利用无模糊DOA粗估计、目标的双基地距离信息以及双基地MIMO雷达的几何特点,解除DOA、DOD精估计的周期性模糊,得到高精度且无模糊的DOA和DOD估计. 最后,根据ESPRIT算法原理和估计误差的概率统计特性进行算法的性能分析,给出算法基线模糊门限的近似计算方法. 该算法有效地放宽了发射阵列孔径扩展程度的限制,从而提高了阵列在大孔径下的角度估计精度,且能够实现DOA和DOD估计的自动配对. 仿真结果验证了所提算法和性能分析方法的有效性.

关键词双基地MIMO雷达;分布式阵列;接收角估计;发射角估计;解模糊;性能分析

引言

双基地多输入多输出(Multiple-Input Multiple-Output, MIMO)雷达,因为其与传统雷达相比在反隐身、抗干扰、抗反辐射导弹、自由度、角度分辨率和测角精度等方面具有优势[1-3],在近几年受到了学术界的广泛关注,而发射方位角(Direction of Departure,DOD)和接收方位角(Direction of Arrival,DOA)估计是双基地MIMO雷达的研究热点之一[1-6]. 文献[4]提出了一种基于旋转不变估计技术(Estimation of Signal Parameters via Rotational Invariance Techniques,ESPRIT)的DOD和DOA估计算法,但该算法需要进行额外的配对操作. 在文献[4]的基础上,文献[5]利用了ESPRIT算法的自身特点实现了DOD与DOA的自动配对. 文献[6]结合了ESPRIT和降维多重信号分类(Multiple Signal Classification, MUSIC)两种算法的特点,提出了一种自动配对的DOD-DOA联合估计方法. 然而以上算法均要求阵元间距小于半波长,考虑到系统的软硬件成本,阵列的物理孔径将受到控制,进而一定程度上限制了这些算法的测角性能.

双基地MIMO雷达利用分布式阵列[7]布阵可以在不增加阵元的前提下,扩展阵列的物理孔径,进而有效提高测角精度. 但是分布式阵列的合成方向图存在高栅瓣[8],将导致测角模糊影响测角性能. 为了避免模糊对测角性能的影响,通常使用双尺度法解测角模糊[9-10]. 文献[9]提出了一种基于双尺度酉ESPRIT(U-DR-ESPRIT)的双基地MIMO雷达DOA和DOD联合估计方法. 但是,该方法在解模糊时,需要进行无模糊精度低的粗估计与有模糊精度高的精估计之间的配对操作. 而且,常规双尺度ESPRIT算法在分布式阵列的子阵间间距较大时,解模糊的效果较差,这将极大地限制该方法对阵列孔径的扩展程度.

针对上述问题,文章参考了ESPRIT算法的基本原理和文献[5]所述方法的自动配对原理,在获得DOD精估计和DOA粗、精估计的同时使其自动配对,避免了额外的配对操作,并且通过引入目标的距离信息和双基地雷达的几何关系对常规双尺度ESPRIT算法的解模糊过程进行改进,有效地放宽了发射阵列孔径扩展程度的限制. 此外,文中根据ESPRIT算法原理和估计误差的概率统计特性对所提算法进行了性能分析,并且给出了算法基线模糊门限的近似计算方法,通过该方法可以计算出所提算法的最大扩展孔径的近似值.

1信号模型

双基地分布式MIMO雷达系统如图1所示,M个阵元的发射阵列和N个阵元的接收阵列分别是由两个阵元间距d=λ/2(λ为入射信号波长)的均匀线阵子阵组成的分布式阵列. 其中,子阵阵元数分别为M′=M/2和N′=N/2,子阵间基线长度分别为DT和DR.

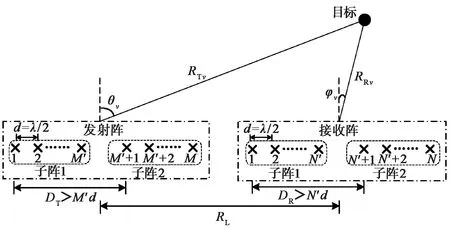
图1　双基地分布式阵列MIMO雷达阵列示意图

假设发射阵列的M个阵元同时发射相互正交的窄带波形信号,这些信号经过处于同一双基地距离单元的V个不相关的远场目标散射传回N个接收阵元. 其中,RL为发射阵与接收阵之间的双基地基线距离,RTv和RRv分别为第v(v=1,2,…,V)个目标距离发射阵和接收阵的距离,RB=RTv+RRv为双基地距离和. 则接收信号经过匹配滤波器后的输出可以表示为

y(t)=As(t)+n(t).

(1)

αv为目标回波幅度,fv为目标多普勒频率; n(t)为独立的加性高斯白噪声.

2算法描述

(2)

式中: Us为V个大特征值对应的特征向量张成的信号子空间; Σs为大特征值组成的对角阵. 在理想情况下,信号子空间与阵列导向矩阵张成的空间相同,则存在唯一的非奇异矩阵T,使得

Us=AT.

(3)

(4)

2.1DOD和DOA的粗估计与精估计

首先,如图1所示,将接收阵列每个子阵的前N′-1个阵元与后N′-1个阵元分别组成子阵rc1、rc2,则子阵rc1和rc2间存在以下形式的旋转不变关系为

Wrc2ar(γv)=ej2πdγv/λWrc1ar(γv).

(5)

式中,Wrc1=I(2)⊗[I((N′-1)M)0(N′-1)M×M]和Wrc2=I(2)⊗[0(N′-1)M×MI((N′-1)M)]为选择矩阵,I(i)表示i阶单位阵,0i×j表示i×j阶0阵. 考虑所有V个信号,式(5)可以表示为矩阵形式为

Wrc2A=Wrc1AΘrc.

(6)

Wrc2Us=Wrc1UsΩrc.

(7)

式中,Ωrc=T-1ΘrcT,Θrc=F-1ΩrcF,F=T-1. 对方程(7)用最小二乘法求解,可以得到

Ωrc=[(Wrc1Us)H(Wrc1Us)]-1·

(Wrc1Us)H(Wrc2Us).

(8)

对Ωrc进行特征值分解,可以得到:

(9)

(10)

将图1所示的发射阵列中子阵1的M′个阵元与子阵2的M′个阵元分别构成子阵tf1、tf2,则子阵tf1和tf2间的旋转不变关系可以表示为如下矩阵形式为

Wtf2A′=Wtf1A′Θtf.

(11)

定义一个新的导向矩阵

(12)

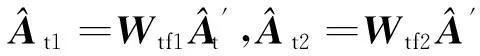
(13)

则精度高但是有模糊的DOD方向余弦估计(称之为DOD精估计),可以由下式计算得到

(14)

同理,将图1中接收阵列中子阵1的N′个阵元与子阵2的N′个阵元分别构成子阵rf1、rf2,则子阵rf1和rf2间的旋转不变关系可以表示为矩阵形式

Wrf2A=Wrf1AΘrf.

(15)

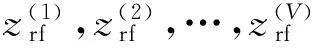
定义一个新的导向矩阵

(16)

(17)

则精度高但是有模糊的DOA方向余弦估计(称之为DOA精估计),可以表示为

(18)

2.2解模糊

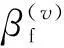
(19)

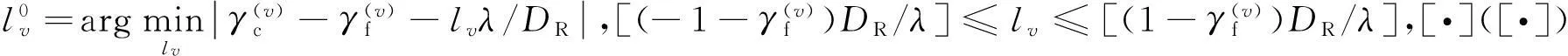
根据双基地雷达的几何特点,可以推出θv与φv存在如下关系式[12]

(20)

(21)

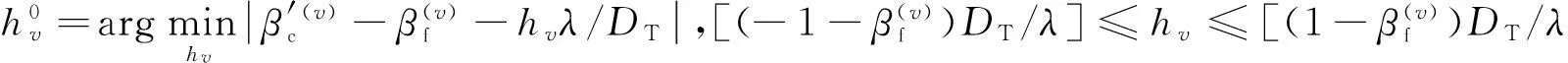
3算法的性能分析

文章所提算法的解模糊过程中利用了目标的双基地距离和RB与双基地基线距离RL,RL可以根据发射阵和接收阵的全球定位系统(Global Positioni-

ng System, GPS)信息计算得到,GPS的定位精度高,因此计算得到的RL可以认为与实际的双基地基线距离是近似相等的.RB可以通过匹配滤波的结果得到,但是这样得到的双基地距离和信息通常是存在一定误差的,该误差可能导致解模糊错误,从而影响算法的测角性能. 因此,本节主要对所提算法进行性能分析,讨论RB的误差对算法测角性能的影响,并且推导了最大可扩展孔径的近似计算方法.

(22)

P(|Δφ(v)f|<Δφ(v)f) =∫Δφ(v)f-Δφ(v)f12πσφ(v)fe-η22σ2φ(v)f()dη

=ρ.

(23)

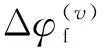
(24)

将式(24)代入式(23)可以得到

(25)

式中: erf-1(·)为误差函数的反函数;通常取ρ=0.998 7[15].

(26)

(27)

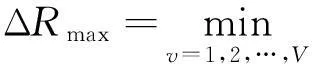
(28)

即阵列结构确定且SNR一定的条件下,当双基地距离和误差ΔR小于上述条件确定的ΔRmax时,DOD精估计可以正确解模糊.

如果不考虑测角误差,则式(27)可以表示为

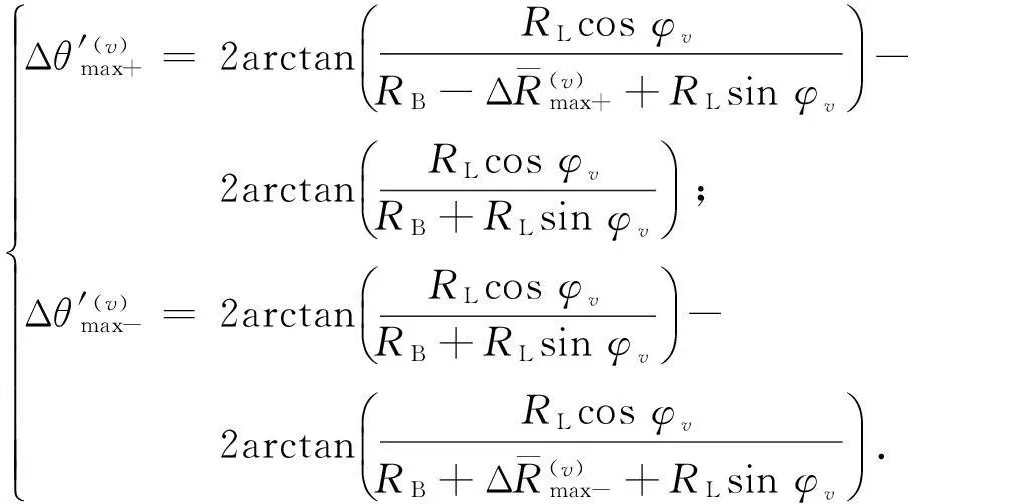
Δθ'(v)max+= 2arctanRLcosφvRB-ΔR(v)max++RLsinφvæèçöø÷- 2arctanRLcosφvRB+RLsinφvæèçöø÷;Δθ'(v)max-= 2arctanRLcosφvRB+RLsinφvæèçöø÷- 2arctanRLcosφvRB+ΔR(v)max-+RLsinφvæèçöø÷.ìîíïïïïïïïïïïïï

(29)

用推导式(28)相同的方法可以得到不考虑测角误差情况下的最大距离和误差为

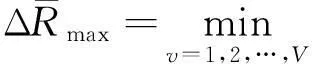
(30)

分布式阵列存在一个基线模糊门限[17],该模糊门限体现了在SNR一定的条件下分布式阵列孔径的最大扩展程度. 因为所提方法对解模糊过程改进的主要效果有效地提高了发射阵列的最大可扩展孔径,所以，这里主要讨论发射阵的基线模糊门限. 利用类似上述分析最大距离和误差ΔRmax的方法可以推导出本文算法中发射阵的基线模糊门限.

在SNR和双基地距离和误差ΔR一定的条件下,根据式(22)和式(26)建立以DT为自变量的方程:

(31)

(32)

(33)

4计算机仿真结果与分析

仿真1目标参数估计与配对

假设该双基地分布式MIMO雷达系统发射阵元数M=16,接收阵元数N=12,发射阵子阵间基线长度DT=60λ,接收阵子阵间基线长度DR=30λ,信号波长λ=1 m,双基地基线距离RL=20 km,目标双基地距离和RB=100 km,目标数V=5,目标DOD为θ=[-20°,-10°,0°,10°,20°],目标DOA为φ=[-39.953 2°,-31.554 7°,-22.619 9°,-13.065 5°,-2.811 3°],快拍数L=20,阵元SNR为0 dB. 图2给出了500次Monte Carlo实验目标参数估计的结果图. 从图2可以看出文章所提算法可以正确估计且自动配对目标DOD和DOA.

图2　DOD和DOA估计结果图

仿真2双基地距离和误差对估计结果的影响

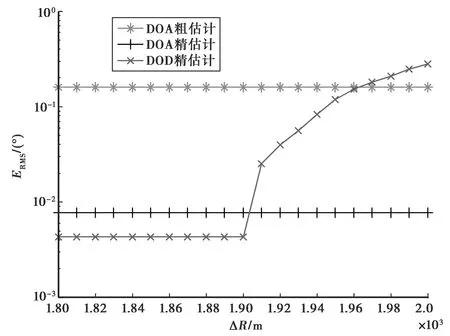
(a) 考虑测角误差

(b) 不考虑测角误差图3　DOD和DOA估计的均方根误差ERMS随ΔR变化图

仿真3估计性能与信噪比的关系

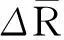
图4　DOD和DOA估计的均方根误差ERMS随SNR变化图

仿真4估计性能与发射阵子阵间基线长度的关系

图5　　　DOD和DOA估计的均方根误差ERMS　　　随发射阵子阵间基线长度变化图

5结论

文章提出了一种双基地分布式阵列MIMO雷达的DOA和DOD估计方法. 该方法利用ESPRIT算法的自身特点在获取DOA粗、精估计和DOD精估计的同时使其自动配对,避免了常规双尺度ESPRIT算法解模糊时所需要进行的额外的配对操作,并且在解模糊过程中引入了双基地MIMO雷达的几何关系和目标的双基地距离信息,使该方法与常规双尺度ESPRIT算法相比有效地放宽了发射阵列孔径扩展程度的限制,提高了测角的性能. 此外,文中对所提算法的性能进行了理论分析,并且给出了最大距离误差和基线模糊门限的近似计算方法,这些分析方法对设计双基地分布式阵列MIMO雷达具有一定的参考价值.

参考文献

[1]程院兵, 顾红, 苏卫民. 双基地MIMO雷达发射波束形成与多目标定位[J].电波科学学报, 2012, 27(2): 275-281.

CHENGYB,GUH,SUWM.Transmitbeamformingandmulti-targetlocalizationinbisaticMIMOradar[J].Chinesejournalofradioscience, 2012, 27(2):275-281. (inChinese)

[2] 陈显舟, 杨源, 韩静静, 等.双基地多入多出雷达收发方位角联合估计算法[J].电波科学学报, 2013, 28(1): 176-182.

CHENXZ,YANGY,HANJJ,etal.JointDODandDOAestimationusingpolynomialrootingforbistaticMIMOradar[J].Chinesejournalofradioscience, 2013, 28(1):176-182. (inChinese)

[3] 樊劲宇, 苏卫民, 顾红, 等. 扩展孔径的电磁矢量多入多出MIMO雷达目标定位算法[J].电波科学学报, 2014, 29(4): 610-615.

FANJY,SUWM,GUH,etal.TargetlocalizationforapertureextendingMIMOradarwithelectromagneticvectorantenna[J].Chinesejournalofradioscience, 2014, 29(4): 610-615. (inChinese)

[4]CHENDF,CHENBX,QINGD.AngleestimationusingESPRITinMIMOradar[J].Electronicsletters, 2008, 44(12): 770-771.

[5]CHENJL,GUH,SUWM.AngleestimationusingESPRITwithoutpairinginMIMOradar[J].Electronicsletters, 2008, 44(24): 1422-1423.

[6]HSUCH,LIUHC,HUAMC.JointDOD—DOAestimationbasedonsignalsubspaceapproachinMIMOradars[J].Wirelesspersonalcommunications, 2014, 77: 951-961.

[7]NILSSONE,WARSTONH.Radarwithseparatedsubarrayantennas[C]//2003RadarConference.Adelaide, 2003: 194-199.

[8]WILSONMJ,MCHUGHR.Sparse-periodichybridarraybeamformer[J].IETradarsonar&navigation, 2007, 1(2): 116-123.

[9]ZHENGGM,CHENBX.Unitarydual-resolutionESPRITforjointDODandDOAestimationinbistaticMIMOradar[J].Multidimensionalsystemsandsignalprocessing, 2015, 26: 159-178.

[10]郑桂妹, 杨明磊, 陈伯孝, 等. 干涉式矢量传感器MIMO雷达的DOD/DOA和极化联合估计[J].电子与信息学报, 2012, 34(11): 2635-2641.

ZHENGGM,YANGML,CHENBX,etal.JointDOD/DOAandpolarizationestimationforinterferometricMIMOradarwithelectromagneticvectorsensors[J].Journalofelectronics&informationtechnology, 2012, 34(11): 2635-2641. (inChinese)

[11]MAY,CHENBX,YANGML,etal.AnovelESPRIT-basedalgorithmforDOAestimationwithdistributedsubarrayantenna[J].Circuits,systemandsignalprocessing, 2015, 34(9): 2951-2972.DOI: 10.1007/s00034-015-9987-6

[12]JACKSONMC.Thegeometryofbistaticradarsystems[J].IEEproceedings, 1986, 133 (7): 604-612.

[13]OTTERSTENB,VIBERGM,KAILATHT.PerformanceanalysisofthetotalleastsquaresESPRITalgorithm[J].IEEEtransactionsonsignalprocessing, 1991, 39: 1122-1134.

[14]RAOBD,HARIKVS.PerformanceanalysisofESPRITandTAMindeterminingthedirectionofarrivalofplanewavesinnoise[J].Transactionsonacoustics,speech,andsignalprocessing, 1989, 37:1990-1995.

[15]LEMMAAN,VEENAVD,DEPRETTEREEF.MultiresolutionESPRITalgorithm[J].IEEEtransactionsonsignalprocessing, 1999, 47: 1722-1726.

[16]TREESHLV.Detection,estimation,andmodulationtheory,partIV:optimumarrayprocessing[M].NewYork:Wiley, 2002.

[17]ATHLEYF.Thresholdregionperformanceofmaximumlikelihooddirectionofarrivalestimators[J].IEEEtransactionsonsignalprocessing, 2005, 53: 1359-1373.

DOD and DOA estimation in bistatic MIMO radar with distributed subarray antennas

MA YanCHEN Baixiao

(NationalLaboratoryofRadarSignalProcessing,XidianUniversity,Xi’an710071,China)

AbstractCombining the characteristics of distributed subarray antennas (DSA) and bistatic multiple-input multiple-output (MIMO) radar, a novel algorithm for direction of departure (DOD) and direction of arrival (DOA) estimation is proposed. First, according to spatial rotational invariance of transmitting array and receiving array, we use estimation of signal parameters via rotational invariance techniques (ESPRIT) algorithm to obtain the non-ambiguous coarse DOA estimation and the high accurate but cyclically ambiguous fine DOD and DOA estimation. Then, the high accurate and unambiguous DOD and DOA estimation can be obtained by using the non-ambiguous coarse DOA estimation, range information of targets, and the geometry of bistatic MIMO radar to disambiguate the above mentioned cyclic ambiguity. Last, the performance of the proposed algorithm is analyzed according to the ESPRIT algorithm principle and the statistic characteristics of estimation error. We also give an approximate method for calculating baseline threshold. The proposed algorithm relaxes the restriction on the aperture of transmitting array, and the accuracy of angle estimation is improved under large aperture array. Moreover, the DOD and DOA estimation using our method is automatically paired. Simulation results show the good performance of proposed method and the effectiveness of performance analysis method.

Keywordsbistatic multiple input multiple output (MIMO) radar; distributed subarray antennas (DSAs); direction of arrival (DOA) estimation; direction of departure (DOD) estimation; disambiguation; performance analysis

收稿日期：2015-06-02

中图分类号TN958

文献标志码A

文章编号1005-0388(2016)02-0228-08

DOI10.13443/j.cjors.2015060201

作者简介

马严(1988-),男,陕西人,博士研究生,研究方向为阵列信号处理.

陈伯孝(1966-),男,安徽人,教授,博士生导师,研究方向为新体制雷达系统设计、阵列信号处理、精确制导与目标跟踪等.

马严, 陈伯孝. 双基地分布式阵列MIMO雷达的DOA和DOD估计方法[J]. 电波科学学报,2016,31(2):228-235. DOI: 10.13443/j.cjors.2015060201

MA Y, CHEN B X. DOD and DOA estimation in bistatic MIMO radar with distributed subarray antennas[J]. Chinese journal of radio science,2016,31(2):228-235. (in Chinese). DOI: 10.13443/j.cjors.2015060201

资助项目: 国家自然科学基金(No.61101244)

联系人： 马严 E-mail: ma_yan_885@163.com