压印机入口坯饼柔性分散机构的开发研究

丘盛昌,　安　琦

(华东理工大学机械与动力工程学院,上海 200237)

压印机入口坯饼柔性分散机构的开发研究

丘盛昌,安琦

(华东理工大学机械与动力工程学院,上海 200237)

摘要：针对压印机在生产过程中出现的坯饼团聚问题,开发了一种利用弹簧为搅拌元件的柔性分散机构,通过竖直悬挂的若干个弹簧对硬币的弹拨作用,实现坯饼的有效分散功能。通过力学建模,建立了这种柔性分散机构的碰撞分离模型以及弹簧尺寸参数的优化模型,结合一个压印机的具体结构参数,采用惩罚函数法(SUMT)对优化模型进行了数值模拟优化,得到分散机构工作弹簧的最佳尺寸参数,实验证明该分散机构具有良好的分散效果。

关键词：压印机; 坯饼团聚; 分散机构; 参数优化; 惩罚函数法

硬币的生产事关国家的经济命脉,硬币生产的关键设备是压印机。压印机在实际工作中常常出现输饼转盘中坯饼的团聚现象,坯饼以层叠的形式随着转盘转动，由于在滑道的入口处存在高度限制,这些层叠的坯饼无法顺利进入滚道,因此可能出现堵塞滑道入口现象,进而影响生产的正常进行。目前有许多学者对压印机进行了研究,包括压印机的结构设计及运动仿真[1-2]、压印精度的提高[3-4]、压印机的动力系统[5]等,但鲜见对坯饼进口的团聚现象进行研究。

通过调研发现,现有的一些分离机构并不能很好地满足对团聚的坯饼的有效分离[6-8]。因此本文构建了一种用弹簧作为柔性搅拌元件的柔性搅拌机构,并通过对弹簧的优化设计,实现了压印机入口硬币的有效分散。

1坯饼团聚现象分析

图1所示为某企业进行硬币生产所采用的某型号卧式压印机,其工作原理见图2。在工作时,一批坯饼倾倒在旋转的输饼转盘上,由于离心力的作用,坯饼被甩到输饼转盘的边缘并被外壳体限制径向位置;坯饼在输饼转盘的边缘和转盘一起运动,当到达外壳体上的出口也即滑道入口时,坯饼被甩离转盘进入滑道,顺着滑道下滑进入压印模具,在中圈承受来自左模和右模的压力产生变形,压印完成后由旋转的中圈将成品送到出口,进入后续的输送部件。

图1　某型号压印机结构图

图2　压印机工作原理图

在生产过程中常常发现输饼转盘中的坯饼聚集成堆而难以分离,并且始终以层叠的方式随着转盘转动。由于在滑道的入口处存在高度限制,这些层叠的坯饼无法顺利进入滚道,并且可能出现图3所示的堵塞滑道入口的情况,从而影响生产的正常进行。为此需要构建坯饼进口分散机构,确保坯饼在转盘上的有效分散。

2分散机构的构建原理

为了解决压印机入口处坯饼团聚问题,本文根据坯饼的堆积情况,构建了一种利用弹簧的弹拨作用而形成的一种柔性打散机构，具体方案如图4所示。将压缩弹簧用支架固定在输饼转盘的上方,弹簧与机架固定,弹簧底端与转盘的距离始终保持在介于一个坯饼和两个坯饼之间的厚度,坯饼在摩擦力的作用下随着转盘运动,并与弹簧碰撞,弹簧由于坯饼的作用,始终处于往复振动状态,对坯饼不断击打,从而实现坯饼的分离。这样的原理类似于一个搅拌器,弹簧类似于其中的搅拌桨,这种搅拌是一种柔性搅拌过程。

图3　滑道入口堵塞情况示意图

图4　分散机构原理图

3机构建模及性能参数优化

3.1分散机构等效图及尺寸参数

本文设计的柔性搅拌机构能否实现最有效的分散功能,关键在于弹簧参数的选取,包括弹簧圈数、簧丝直径、节距、弹簧中径等参数。为此,通过力学建模和数值模拟优化,对弹簧参数进行了深入研究。

本文所构建的柔性搅拌机构的核心元件是弹簧,其工作原理及坯饼尺寸如图5所示。图中v为转盘外缘的线速度,L为弹簧长度,me为弹簧自由端等效质量,mp为坯饼质量,dp为坯饼直径,h为坯饼厚度。坯饼与转盘之间由于摩擦力作用无相对运动,取x方向为矢量的正方向。

3.2确定弹簧自由端等效质量

图4所示是一种非线性振动的弹簧质量系统。根据文献[9],弹簧的高度越高,弹簧质量系统的振动越接近简谐振动。本文中弹簧具有相当的高度,且仅需考虑1/2个周期,因此将其按简谐振动处理。假设做简谐振动的弹簧质量系统中弹簧的总质量为m,则弹簧的等效质量me为[10-13]

图5　分散机构等效图及尺寸参数

(1)

其中:ρ为弹簧钢密度；d为弹簧丝径；D2为弹簧中径；n为弹簧圈数；α为弹簧螺旋升角。

3.3第1次碰撞

假设分散机构开始工作时,弹簧处于竖直静止状态,坯饼随着转盘以一定的速度vp(vp=v)撞上弹簧自由端。假设发生的碰撞为完全弹性碰撞,且能够使堆积的坯饼分离。碰撞后弹簧自由端产生向左的速度ve1,坯饼速度为vp1,碰撞产生动载荷为Fd1，如图6所示。

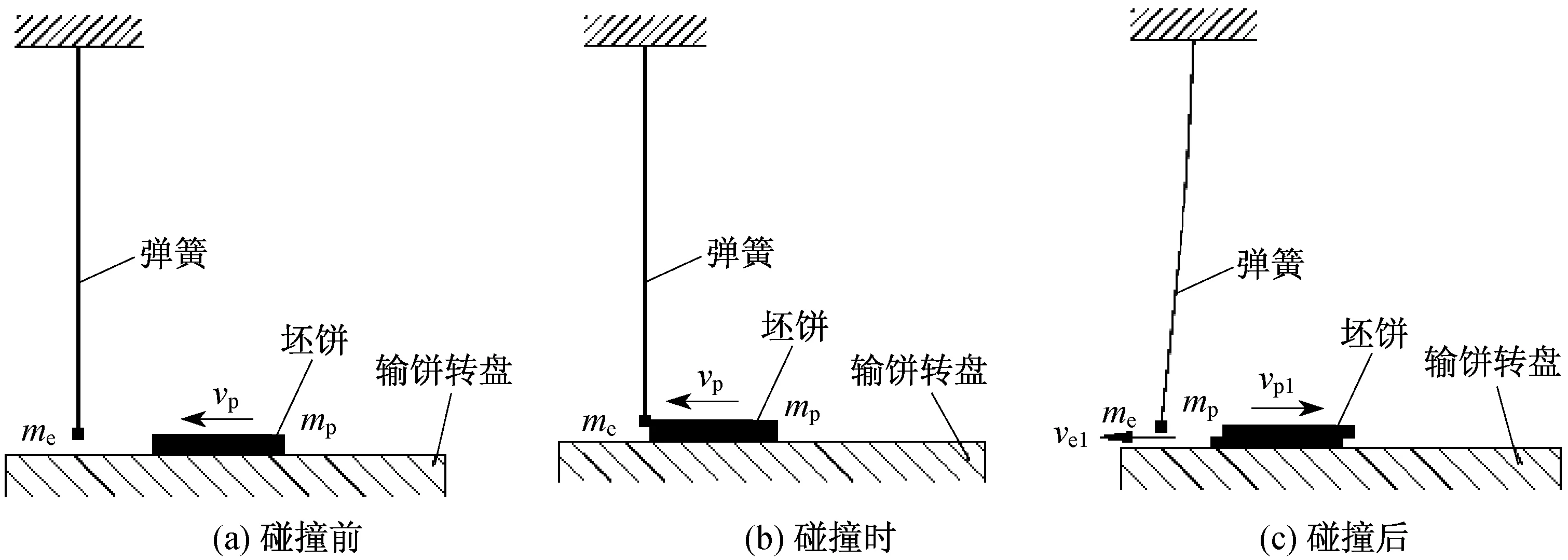
图6　第1次碰撞过程示意图

根据动量和能量守恒定律,可得

(2)

碰撞后的弹簧满足能量守恒,可得

(3)

式中：x1为第1次碰撞弹簧达到最大变形量时自由端的位移；自由端横向刚度KH=k(x)是自由端位移的函数,也可以根据文献[14]表示为横向作用力FH的函数。

坯饼与弹簧之间由于碰撞产生的动载荷为

(4)

式中:g为重力加速度;P为静载荷,P=mpg;Δst为弹簧在P作用下的静位移。联立式(2)和式(3),可得

(5)

3.4第2次碰撞

第1次碰撞结束后,坯料被分离,后续坯饼继续与弹簧发生碰撞,假设碰撞发生于弹簧回弹到竖直状态时,则坯饼恰好运动到弹簧的竖直位置。假设碰撞时坯饼速度为vp,弹簧自由端速度为-ve1,碰撞后弹簧自由端得到速度ve2,坯饼速度变为vp2,碰撞产生动载荷为Fd2,碰撞过程如图7所示。

图7　第2次碰撞过程示意图

根据动量及能量守恒定律,可得到第2次碰撞的力学关系为

(6)

不考虑碰撞过程的能量损失,碰撞后的弹簧满足能量守恒定律

(7)

式中,x2为第2次碰撞弹簧达到最大变形量时自由端的位移。

第2次碰撞产生的冲击动载荷为

联立式(6)和式(7)可得

(8)

3.5第3次碰撞

第2次碰撞结束后,坯料被分离,后续坯料继续与弹簧发生碰撞,同样假设碰撞发生于弹簧回弹到竖直状态,这时坯饼恰好运动到弹簧的竖直位置。同样假设碰撞时坯饼速度为vp,弹簧自由端速度为-ve2,碰撞后弹簧自由端得到速度ve3,坯饼速度变为vp3,碰撞产生动载荷Fd3,如图8所示。

图8　第3次碰撞过程示意图

根据动量及能量守恒定律,可得

(9)

碰撞后的弹簧满足能量守恒定律

(10)

式中,x3为第3次碰撞弹簧达到最大变形量时自由端的位移。

第3次碰撞产生的动载荷为

联立式(9)和式(10)可得

(11)

3次碰撞之后,机构将进入稳定的重复运行阶段。

由于弹簧自由端从最大位移x3回到平衡位置时的运动是变加速运动,为计算这段位移需要的时间,将这段位移作有限段的等分,每个微段看作匀加速直线运动,可求得弹簧回到平衡位置需要的时间为

(12)

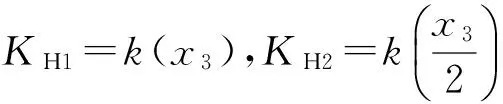
3.6模型优化

要使机构能够正常工作,第1次碰撞产生的动载荷Fd1应大于坯饼之间的咬合力F,可得优化边界条件1如下：

根据弹簧丝径d小于或等于节距p的特征,可得优化边界条件2如下：

综上,优化问题的数学模型为

(13)

针对上述模型,采用适当的优化方法进行优化计算。

3.7惩罚函数法

针对式(13)给出的约束优化问题,可用惩罚函数法进行优化计算。惩罚函数法的基本原理是将约束优化问题中的不等式和等式约束函数经过加权转化后,和原目标结合形成新的目标函数——惩罚函数,并求解该新目标函数的无约束极小值,以期得到原问题的约束最优解[15-16]。由于惩罚函数法具有对方程初始解要求低、迭代收敛速度快的优点[17],简单实用,在优化计算中具有广泛的应用。

根据约束形式和构造的函数及惩罚函数因子的不同,惩罚函数法分为内点惩罚函数法、外点惩罚函数法和混合型惩罚函数法3种,其中外点惩罚函数法由于能够同时解决含有等式和不等式的约束优化问题,而且惩罚函数的构造、初始点的选择没有区域限制,具有收敛速度快的优点[18-19],所以本文采用外点惩罚函数法进行优化计算。

4算例分析

某型号的压印机,由于是在现有的机器上进行改进,使用弹簧的高度L受输饼转盘处空间限制只能取70 mm,弹簧的中径D2受坯饼直径限制只能取8 mm。根据机器参数及实测数据,转盘外缘的线速度v=1.87 m/s,坯饼直径dp=25 mm,厚度h=2.15 mm,质量mp=6.05 g,坯饼之间的咬合力F=0.6 N。现根据前文建立的优化模型,对弹簧的丝径d,圈数n进行优化,使机构能在最佳状态下运行。为便于计算,本文中弹簧的圈数n取整数。

根据文献[20],弹簧的螺旋升角满足

(14)

18≤n≤31(n∈Z)

因此得2.2≤p≤3.98,根据文献[20],可得符合要求的丝径d的取值范围为

d={0.3，0.35，0.4，0.45，0.5，0.6，0.7，0.8，0.9，

采用外点惩罚函数法对式(13)所示的优化模型进行改写,可得带惩罚约束项的目标函数为[19]

(15)

式中,r为惩罚因子。

取惩罚因子r=1 000,根据式(15),按前文求得的圈数及丝径的取值范围取不同的丝径d及圈数n,通过MATLAB编写计算程序,求得最终结果为:当n=21,d=1.2 mm时,fmin=2.35×10-4s。即当弹簧丝径为1.2 mm,中径为8 mm,圈数为21圈时,目标函数最小,此时的尺寸参数为最优值。弹簧最佳尺寸参数如表1所示。按照该组参数设计的压印机坯饼进口分散机构,目前已经通过实验验证,证实具有很好的分散效果,实现了预期的功能。

表1　最佳弹簧几何参数表

5结论

(1)针对压印机工作过程中入口存在的坯饼团聚问题,设计了一种利用弹簧为搅拌元件的柔性分散机构,通过竖直悬挂的若干个弹簧对硬币的弹拨作用,实现坯饼的有效分散功能。

(2)对所构建的压印机入口坯饼柔性分散机构进行研究,通过力学建模,建立了坯饼和分散机构的碰撞分离模型,并建立了弹簧尺寸参数的优化模型，采用惩罚函数法对优化模型进行了数值模拟优化,得到分散机构工作弹簧的最佳尺寸参数。实验证实本文设计的柔性分散机构具有良好的分散效果。

参考文献：

[1]王洪珍.基于Autodesk Inventor11的压印机结构设计及运动仿真[J].机械研究与应用,2011(6):76-78.

[2]王江涛,周炳海.福格森凸轮曲线的测定与分析[J].机械制造,2006,44(10):69-72.

[3]严乐,卢秉恒,丁玉成,等.高精度步进压印机热误差的建模分析[J].西安交通大学学报,2005,39(5):526-530.

[4]严乐,卢秉恒,丁玉成,等.高精度压印机热误差补偿中温度变量的辨识[J].西安交通大学学报,2006,40(7):827-830.

[5]张建新.高频换向快动型压印机液压系统的研究[J].山西机械,2001 (3):40-41.

[6]BENSON R B,COURTEAU W J,PAUL S T，etal.Unstacking Machine:4252484(A)[P].1981-2-24.

[7]许健健,王耕耘,王义林.基于NX7.0的一种自动化冲压生产线板料分离机构的设计[J].锻压装备与制造技术,2012(1):13-16.

[8]彭国庆,陈柏金.基于气动机械手的自动化冲压生产线的设计[J].锻压技术,2012,37(3):85-88.

[9]黄焱,何松林.弹簧质量系统非线性振动的实验研究[J].昆明学院学报,2014,36(6):66-68.

[10]丁履成,司明扬.有质量的弹簧的振动问题[J].大学物理,1985(9):15-19.

[11]罗蔚茵.关于弹簧振子固有频率的进一步讨论[J].大学物理,1985(11):9-11.

[12]孙春峰.弹簧的质量、材料及其几何性质对弹簧谐振子角频率的影响[J].大学物理,1993(12):20-21.

[13]刘大鹏,关荣华.弹簧质量对弹簧谐振子圆频率的影响[J].大学物理,1995(10):22-24.

[14]丘盛昌,安琦.圆柱螺旋弹簧横向刚度的计算方法研究[J].华东理工大学学报(自然科学版),2015,41(6):846-851.

[15]安琦,顾大强.机械设计[M].北京:科学出版社,2008:400-420.

[16]孙靖民,梁迎春.机械优化设计[M].北京:机械工业出版社,2006:145-151.

[17]HAN S P,MANGASARIAN O.Exact penalty functions in nonlinear programming[J].Mathematical Programming,1979,17(1):251-269.

[18]何力,王琴芳.惩罚函数法在发动机性能计算中的应用[J].南京航空航天大学学报,2001,33(4):338-341.

[19]殷晓飞,任晓丹.基于VB外点惩罚函数法的实现[J].装备制造技术,2011(3):64-66.

[20]MOHAMMAD R T,FEREIDOUN A.Optimizing structural active control force using the exterior penalty function method[J].AIP Conference Proceedings,2008,1020(1):1245-1252.

Blank Dispersing Mechanism for Stamping Machine

QIU Sheng-chang,AN Qi

(School of Mechanical and Power Engineering,East China University of Science and Technology,Shanghai 200237,China)

Abstract:Stacking blank in stamping machine was studied and a blank dispersing mechanism using springs hanged above the stacking blank to disperse was developed.The model of the collision between the blank and the spring was established through the mechanical analysis.Based on the collision model,the optimized model for selecting spring was established,and on the basis of the parameters of a stamping machine,the SUMT was used to numerically calculate the optimized model and the optimum parameters of the spring which was used in the dispersing mechanism were obtained.The developed blank dispersing mechanism was proved to work well through experiment.

Key words:stamping machine; stacking of blank; dispersing mechanism; parameter optimization; SUMT

收稿日期：2015-06-15

作者简介：丘盛昌(1990-),男,福建人,硕士生,研究方向为机械设计及理论。 通信联系人：安琦,E-mail:anqi@ecust.edu.cn

文章编号：1006-3080(2016)02-0291-06

DOI:10.14135/j.cnki.1006-3080.2016.02.022

中图分类号：TH135+.1

文献标志码：A