一些扫帚图的Ramsey数

余　培， 陈　明， 李雨生

(同济大学 数学系，上海 200092)



一些扫帚图的Ramsey数

余培， 陈明， 李雨生

(同济大学 数学系，上海 200092)

摘要：给定图G，Ramsey数R(G)是最小的正整数N，满足对完全图 KN的边任意红蓝着色，则或者存在红色子图G或者存在蓝色子图G.扫帚图Bk，m是将星图K1,k的中心点与路Pm的一个端点黏成一个点得到的树图.由此得到,当k为大于1的正整数时，R(Bk,2k-1)=4k-2且R(Bk,4)=2k+3.

关键词：Ramsey数； 树； 扫帚图

1研究背景

本文研究的图均为简单图.任给图G和H，Ramsey数R(G,H)是最小的正整数N，满足对完全图KN的边任意红蓝着色，则或者存在红色子图G或者存在蓝色子图H.当G=H时，简记R(G,G)为R(G).

Ramsey数一直都是国际上比较热门的研究课题之一.以Tn表示具有n个点的树.作为最简单的图类，R(Tn)的研究备受关注.其中两类经典的图类是星图和路. 记K1,n-1是星图，也即一个点下面挂了n-1条边；Pn是有n个点的路.它们的Ramsey数如下,分别见文献[1-3].

-1.

本文的研究对象是扫帚图Bk,m.扫帚图Bk，m是将星图K1,k的中心点与路Pm的一个端点黏成一个点后所得到的树图.由定义可知：B1,m是路Pm+1；Bk,1=K1,k,Bk,2=K1,k+1是星图.Erdös,Faudree等人在文献[4]中得到：R(Tn)的最小下界能在某些Bk,m中达到，同时猜测R(Tn)的最大上界也能在某些Bk,m中达到，故研究R(Bk,m)是非常有意义的.

目前扫帚图研究的主要结果是Erdös,Faudree等人在文献[4]中得到的，如下：

(2) 当5≤m≤2k-1时，R(Bk,m)≤2k+m.

当m=1,2时，Bk,1，Bk,2是星图，由引理2可得到R(Bk,1),R(Bk,2)的值；当m=3时，Bk,3是双星图，Guo和Volkman在文献[5]得到R(Bk,3)的值.因此还未确定的是当m=4，以及当5≤m≤2k-1时的情况.本文得到如下结果.

定理1设k是正整数，则R(Bk,2k-1)=4k-2.

定理2设k≥2为正整数，则R(Bk,4)=2k+3.

2主要结果的证明

已知图G，以V(G)表示图G的顶点集.当给图G的边红蓝染色后，记其中红色子图为R，蓝色子图为B.已知v是图G中的任意点，记N(v)={u|点u，v之间连边}为点v的邻域；NR(v)={u|边[uv]是红色}为点v的红邻域；NB(v)={u|边[uv]是蓝色}为点v的蓝邻域. 二部图G(A,D)：可将图G的顶点集分成两类A和D，边只在A和D之间存在，而A和D内部并没有边的图类.其他有关图的定义，可参考文献[6].

引理3(Jackson)已知G(A,D)是二部图，其中k≤|D|≤2k-2.若A中任意点x均满足|N(x)|≥k，则G(A,D)包含任意圈C2t，其中1≤t≤min{|A|,k}.

引理4已知树Tn的两个部集大小分别为a,b,则

R(Tn)≥max{2a+b-1,2b-1}

证明不妨假设b≥a.给完全图K2a+b-2红蓝边染色，其中红色子图为Ka-1∪Ka+b-1,相对应的蓝色子图为二部图G(a-1，a+b-1)，由于其中一个单色部集最大为a-1达不到a，故不含单色Tn.

给完全图K2b-2红蓝边染色，其中红色子图为Kb-1∪Kb-1,相对应的蓝色子图为二部图G(b-1,b-1),由于单色部集最大为b-1，达不到b,故不含单色Tn.

综上有R(Tn)≥max{2a+b-1,2b-1}，证毕.

推论1已知k,m为正整数，则

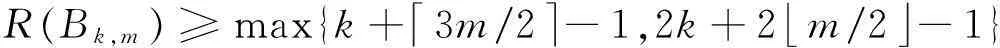
R(Bk,m)≥max{k+3m/2-1,2k+2m/2-1}

定理1的证明当k=1时，B1,1=P2，由Ramsey数的定义知R(P2)=2.

当k=2时，Bk,2k-1=B2,3，由推论1知R(B2,3)≥6，下面来证R(B2,3)≤6.

给完全图K6任意红蓝边染色，则必存在一点的单色度大于等于3，不妨设点v的蓝色邻域大于等于3. 在NB(v)中取集合A0满足|A0|=3，记C=V(K6)(A0∪v),则|C|=2.若A0与C之间存在蓝边，则存在蓝色B2,3；若A0与C之间没有蓝边，即全是红边，此时A0与C之间存在红色B2,3，故R(B2,3)=6.

当k≥3时，由推论1知R(Bk,2k-1)≥4k-2，下面只需证R(Bk,2k-1)≤4k-2.

给完全图K4k-2任意红蓝边染色，记染色后的图为G.根据Ramsey数的定义，只需证明G中含有单色Bk,2k-1.由文献[7]知：当k≥3时，R(C2k)=3k-1. 因4k-2≥3k-1，所以G中含有单色C2k,不妨设其为蓝色.

记D=V(G)V(C2k),则|D|=2k-2. 若C2k中存在一点x满足：|NB(x)∩D|≥k-1,则G中存在蓝色Bk,2k-1. 假设对C2k中任意点x，均有|NB(x)∩D|≤k-2.由|NB(x)∩D|+|NR(x)∩D|=|D|=2k-2知，|NR(x)∩D|≥k，故V(C2k)和D之间至少有2k2条红色边.从而D中存在一点u满足|NR(u)∩V(C2k)|≥2k2/|D|≥k+1.在NR(u)∩V(C2k)中选取k+1个点{u0,u1,…,uk},记集合A=V(C2k){u1,u2,…,uk},则|A|=k.

考虑红色二部图G(A,D)∩R. 该红色二部图满足引理3的条件，故A和D之间存在红色圈C2k.记该红圈的顶点集为E.由于该红色圈包含A，从而包含点u0.此时{u1,u2,…,uk}，u，u0，E可生成红色Bk,2k-1.证毕.

当k=1时，B1,4=P5，由引理1知，R(P5)=6；当k≥2时，Bk，m开始存在星结构，下面考虑此时R(Bk,4)的值.

定理2的证明由推论1知,R(Bk,4)≥2k+3，下面只需证R(Bk,4)≤2k+3.

给完全图K2k+3任意红蓝边染色，设G是染色后的图.由Ramsey数的定义，只需证G含有红色或者蓝色子图Bk,4.下面用反证法来证明，即假设G中不含有单色Bk,4,最终来推出矛盾.

(1) 当k=2时，2k+3=7.由引理1知R(P5)=6≤7，故G中含有单色路P5，不妨设为红色.按顺序标记该路的点为{x1,x2,x3,x4,x5},记路之外的两点为{y1,y2}. 由于不含红色B2,4，故集合{x2,x4}与{y1,y2}之间的边全是蓝色的.

情形1集合{x1,x5}与{y1,y2}之间存在红色边.

不妨假设边[x5,y2]是红色的.由于不含红色B2,4，故边[x5,y1]，[x3,y1]均是蓝色的.此时{x2,x3}，y2，x4，y1，x5可生成蓝色B2,4，矛盾.

情形2集合{x1,x5}与{y1,y2}之间全是蓝色边.

此时易知{x1,x2}，y2，x4，y1，x5可生成蓝色B2,4，矛盾.

故当k=2时，定理成立.

(2) 当k≥3时，由引理2知R(K1,k+1)≤2k+3, 故G中含有单色K1,k+1,不妨设为蓝色.设x为该蓝色K1,k+1的中心点，记A=V(K1,k+1)x，D=V(G)V(K1,k+1)，则|A|=|D|=k+1.

断言D是红色完全图Kk+1,即D内的边都是红色的.

断言的证明用反证法，假设D内存在蓝色边[u,v]. 由于G不含蓝色Bk,4,从而{u,v}和A之间全是红边.若{u,v}和D{u,v}之间存在红色边，则A，{u,v}和该红边可生成红色Bk,4，故{u，v}和D{u,v}之间全是蓝色边.此时选取这些蓝边，按刚刚的分析可知，D内边全是蓝色的且A与D之间的边均为红色.

此时在D中取一点w.若边[x,w]染蓝色，则A，x，w和Dw中任意两点可生成蓝色Bk，4,注意到此时Dw中可取两点，因|D|=k+1≥3；若边[x,w]染红色，此时在Dw中取一点d1，在A中取一点a1，则Aa1，d1，a1，w，x可生成红色Bk,4.无论哪种情形，所得结果均与假设矛盾，故D内边全是红色的，进而断言成立.

下面考虑x与D之间边的染色情况.

情形3x与D之间存在红边.

情形4x与D之间的边全是蓝色的.

此时在A∪D中任取集合F满足|F|=k+1，记M=V(G){F∪x},则|M|=k+1.由断言的分析知：M为红色完全图Kk+1.由F的任意性，可知A∪D是红色完全图K2k+2.由于2k+2≥k+4,故A∪D中含有红色Bk,4，矛盾.故当k≥3时，定理成立.

综上所述，定理成立.证毕.

参考文献:

[1]Burr S, Roberts J. On the Ramsey numbers for stars[J]. Utilitas Mathematica, 1973, 4: 217.

[2]Chvátal V, Harary F. Generalized Ramsey theory for graphs II, small diagonal numbers[J]. Proceedings of American Mathematical Society, 1972, 32(2): 389.

[3]Gerencser L, Gyárfas A. On Ramsey-type problems[J]. Annales Universitatis Scientiarum Budapestinensis de Rolando Eotvos Nominatae Sectio Mathematica, 1967, 10: 167.

[4]Erdös P, Faudree R, Rousseau C,etal. Ramsey numbers for brooms[J]. Congressus Numerantium, 1982, 35:283.

[5]Guo Y, Volkmann L. Tree-Ramsey numbers[J]. The Australasian Journal of Combinatorics, 1995, 11: 169.

[6]Bollobás B. Modern graph theory[M]. New York: Spring-Verlag, 1998.

[7]Faudree R, Schelp R. All Ramsey numbers for cycles in graphs[J]. Discrete Mathematics, 1974, 8(4): 313.

Ramsey Number for Some Brooms

YU Pei， CHEN Ming， LI Yusheng

(Department of Mathematics, Tongji University, Shanghai 200092, China)

Abstract：For a given graph G, Ramsey number R(G) is the smallest integer N such that any red/blue edge-coloring of KN contains a red copy or a blue copy of G. Let broom Bk,mbe a tree obtained by identifying the central vertex of a star K1,kwith an end-vertex of Pm. It is proven that R(Bk,2k-1)=4k-2 and R(Bk,4)=2k+3 for integer k>1.

Key words：Ramsey number; tree; broom

收稿日期：2015-09-07

通讯作者：陈明(1981—)，男，博士生，讲师，主要研究方向为组合数学与图论. E-mail: chen2001ming@163.com

中图分类号：O157.5

文献标志码：A

第一作者： 余培(1993—),男,博士生,主要研究方向为组合数学与图论. E-mail: yupeizjy@163.com