温度场及非均布移动荷载作用下沥青路面力学响应分析

董泽蛟， 潘小康,2， 邵显智， 周兴业

(1. 哈尔滨工业大学 交通科学与工程学院，黑龙江 哈尔滨 150090；2. 公路养护技术国家工程研究中心，北京 100095；3. 中国民航机场建设集团公司，北京 100100；4. 交通部公路科学研究院，北京 100088)



温度场及非均布移动荷载作用下沥青路面力学响应分析

董泽蛟1， 潘小康1,2， 邵显智3， 周兴业4

(1. 哈尔滨工业大学 交通科学与工程学院，黑龙江 哈尔滨 150090；2. 公路养护技术国家工程研究中心，北京 100095；3. 中国民航机场建设集团公司，北京 100100；4. 交通部公路科学研究院，北京 100088)

摘要：为研究路面结构实际温度场对沥青路面结构动力响应的影响，基于路面结构温度场现场实测数据及室内实际路面材料动态模量试验结果，建立温度场分析和非均布移动荷载作用下沥青路面瞬态动力分析三维有限元模型，分析路面结构在实际温度-荷载作用下的动力响应规律，并与传统的等温结构模型动力响应结果进行对比分析.结果表明，层底控温方法模拟出的温度场可用于分析夏季高温时段和低温时段沥青路面的实际动力响应；夏季一天中高温时段，等温模型高估了竖向应变及上、下面层的剪应变，低估了中面层的剪应变；夏季一天中低温时段，沥青路面的实际动力响应大于等温模型的计算值，等温模型低估了温度分布对沥青路面车辙和开裂的影响.

关键词：道路工程； 等温模型； 数值模拟； 动力响应； 温度场； 非均布移动荷载

沥青面层材料是一种典型的温度敏感性材料，其力学特性和使用性能随温度的变化而显著变化.而沥青路面最常见的破坏形式是疲劳开裂和车辙变形，其产生机理和发展过程与路面温度场的分布状况密切相关[1].

为考虑温度对沥青路面结构动力响应的影响，通常采用疲劳等效温度和车辙预估等效温度作为评价路面结构行为特性的参数[2].郑仲浪[3]将路面结构简化为等温结构，计算不同温度下路面材料的模量、路表弯沉值和路面结构的应变.艾长发[4]通过数值模拟得出路面温度场，研究大温差条件下竖向荷载与水平荷载综合作用下路面结构的静力学响应.董忠红等[5]采用红外线加热装置对试验路段加热, 测试不同温度下路面结构的动力响应,研究温度对路面结构动力响应的影响.吕彭民[6]建立了一种移动荷载作用下长大上坡沥青路面动力响应模型，分析温度对路面各动力响应参数的影响规律.

总结现有研究发现，多数研究没有考虑路面结构沿深度方向存在的温度梯度，或从静力学角度研究温度对路面响应的影响，难以评估实际车轮荷载与温度场共同作用下路面结构动力响应规律[7].为此，基于实际路面材料动态模量试验结果和路面结构温度场分布实测数据，建立非均布移动荷载作用下沥青路面瞬态动力分析三维有限元模型，分析路面结构处于实际温度场时的动力响应.

1路面结构温度场分布规律

1.1温度场随时间变化规律

文中研究的试验路路面结构如图1所示.由于路面结构处于复杂的自然环境中，受气温、太阳辐射等影响，其温度场时刻发生着变化.根据吉林长寿命路面结构信息监测项目现场温度场测试结果[8]，试验路路面结构不同深度温度传感器夏季某一天内实测得到的路面温度场数据及气温如图2所示(图中D表示深度).可知，路面温度场时程曲线在一天内先后出现一个波谷和一个波峰，分别对应凌晨时的最低温度和午后的最高温度；测量点距离路表越浅，温度波动幅度越大，最高温度越高，其原因是由于距离路表越浅，受气温、太阳辐射影响越大；测量点距离路表越深，波谷波峰出现的时间越晚，主要是由于热流在路面结构中的传递需要时间；因此，夏季沥青路面下面层长期处于较高温度，对沥青路面结构性能的影响不容忽视.

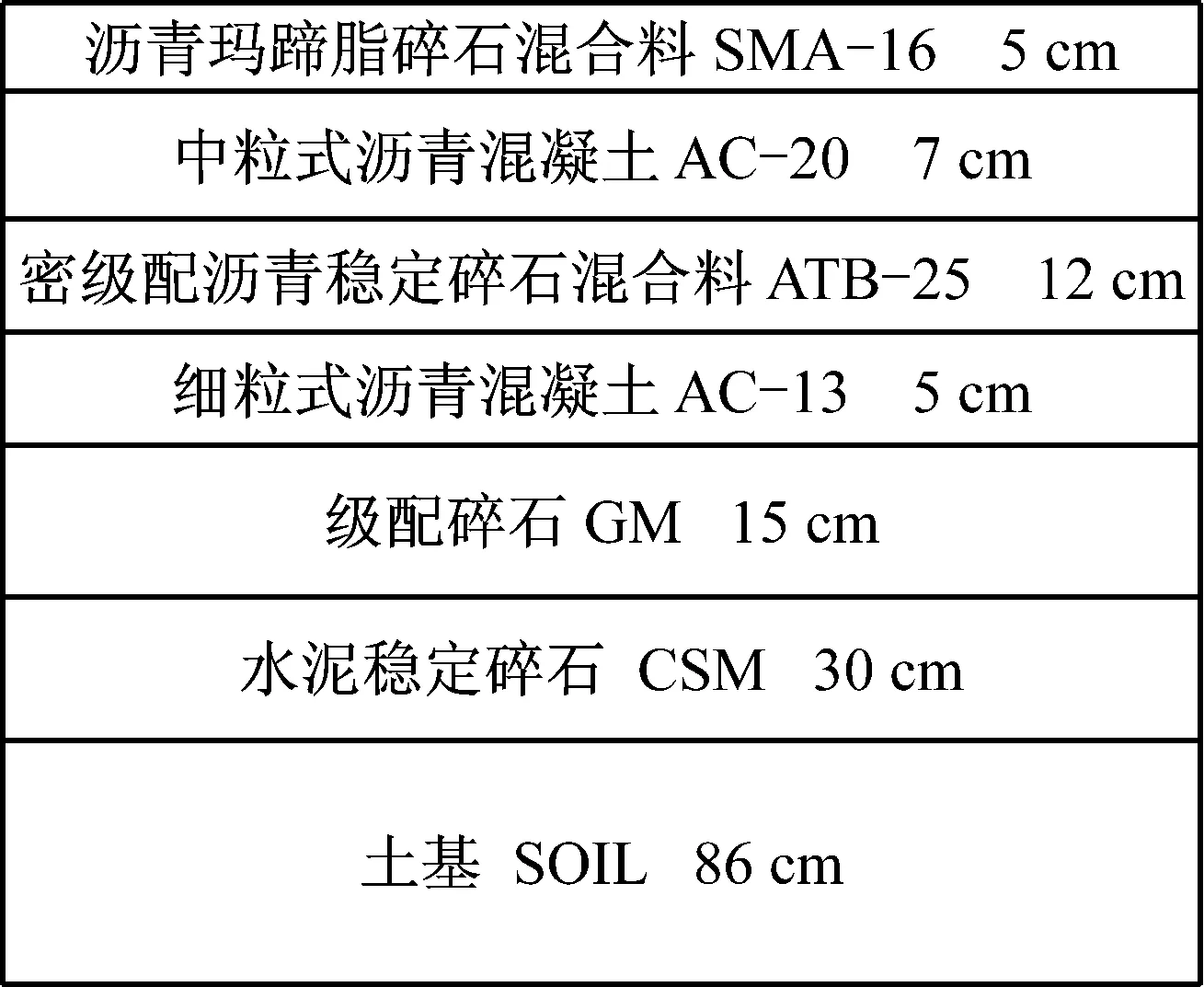
图1　试验路路面结构

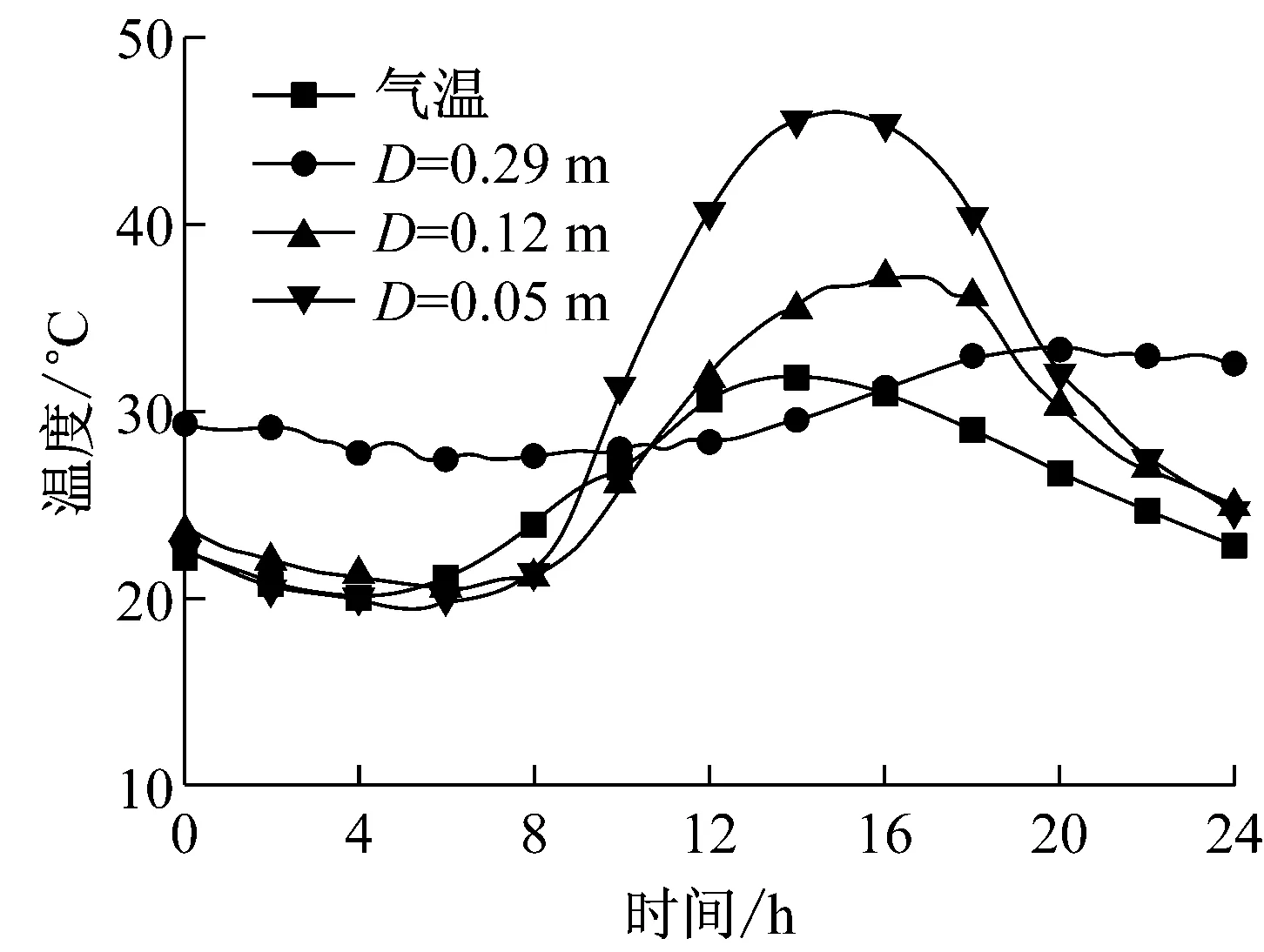
图2　路面温度场随时间变化

1.2温度场模拟

由于路面结构具有一定厚度，受辐射、对流等复杂环境及热流传递的影响，其温度场不仅随时间变化，而且也随深度变化.为获得路面任意深度处的温度，基于ABAQUS软件平台模拟夏季某一天路面结构的温度场分布.

建立沥青路面结构三维有限元模型.赋予各层材料参数，路面材料热物理参数根据相关文献采用参考值[9-10]，如表1所示.在ABAQUS中用DFLUX子程序实现太阳辐射作用，通过相互作用模块的定义实现路面空气辐射换热，用FILM子程序实现对流换热作用[10].为提高温度场模拟的准确性,以路面深度0.29m处的实测温度为控制条件.

表1　路面材料热物理参数

模拟出路面结构任意一点一天内的温度值，为验证温度场模拟的准确性，用路面结构深度为0.05 m及0.12 m处一天内的温度实测值和模拟值进行对比分析，如图3所示.图中D为实测点深度，Z为模型中计算点的深度，下同.

经对比分析可以发现，0.05 m深度处的模拟温度与实测值相似度较高，整体变化趋势基本相同，最大值基本一致,但最小值有一定差别.0.12 m深度处的模拟温度与实测值差异相对较大，最大值最小值皆有一定差别，但有相似的变化趋势.总体来看，层底控温方法模拟的温度场具有一定的适用性.

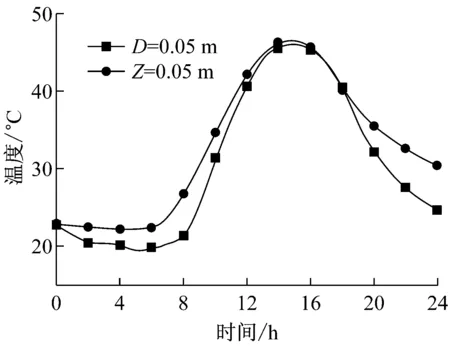
图3　不同测点模拟温度与实测温度对比

Fig.3Comparison of simulated and measured temperature at different points

图4对比分析了高温时段(high temperature period，HTP)及低温时段(low temperature period，LTP)的模拟温度场和实测温度场.从图4中可以发现，尽管模拟出的路面温度场与实际温度场不完全一致，但在夏季高温时段和夏季低温时段，模拟温度场能反映路面结构的实际温度分布规律.表2给出了夏季高温时刻和夏季低温时刻不同深度处模拟值和实测值，可以发现两个时刻的模拟值和实测值比较接近，故可以基于模拟的温度场分析夏季高温时段和夏季低温时段路面结构的实际动力响应.

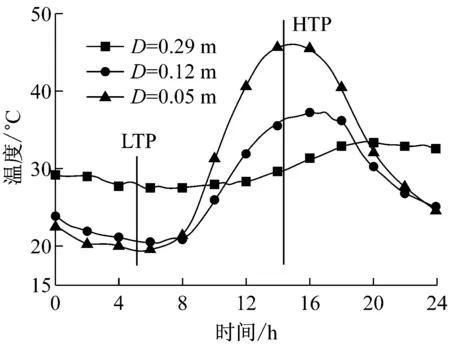
图4　模拟温度与实测温度对比

表2不同深度处模拟及实测温度

Tab.2Simulated and measured temperature at different depths

深度/m夏季高温温度/℃夏季低温温度/℃实测值模拟值实测值模拟值0.0546.146.319.522.10.1236.636.920.723.60.2930.429.628.328.3

1.3温度场空间分布规律

基于温度场模拟结果，表3给出了夏季高温时刻(t=14：00)和夏季低温时刻(t=2：00)时路面结构不同深度处的温度.由表3可知，夏季高温时段，距离路表越浅温度越高，路面结构呈正温度梯度，温度梯度约为73 ℃·m-1.夏季低温时段，距离路表越深温度越高，路表处温度最低，路面结构呈负温度梯度，温度梯度约为-38 ℃·m-1.由此可见，路面结构在一天内存在正负温度梯度交替变化的作用，而等温结构模型不能反映该温度作用行为.因此，关于不同温度分布对沥青路面动力响应的影响需要进一步评估.

表3　路面结构温度分布模拟结果

2动力响应分析有限元模型

由前述测试及模拟结果可知，在同一时刻，路面结构不同深度处的温度明显不同，而沥青路面材料的性能受温度影响较大.为此，建立沥青路面结构三维有限元模型，按夏季高温和夏季低温时段两种情况引入模拟温度场(夏季高温时段用t=14：00时刻的温度场代表，夏季低温时段用t=2：00时刻温度场代表)，施加非均布移动荷载计算路面结构动力响应.与等温结构模型(夏季高温时段对应45 ℃等温结构模型，夏季低温时段对应25 ℃等温结构模型)的模拟结果对比，分析实际温度场对沥青路面结构动力响应的影响[10].

根据前述试验路路面结构，基于ABAQUS软件平台建立三维有限元动力分析模型.模型尺寸竖向(路面结构厚度)1.60 m、纵向1.86 m、横向1.20 m，模型各层采用路面结构实际厚度，模型由加载区域及外侧的影响区域组成.用DLOAD子程序实现非均布移动荷载的数值模拟，荷载移动速度为36 km·h-1.分析时通过预定义场调用温度场模拟结果.有限元模型及移动荷载如图5所示，非均布移动荷载等的详细信息见参考文献[11]，这里不加赘述.

a 有限元模型

b 移动荷载模型

沥青面层采用实测材料参数，参照美国ASTM D-3497(动态模量试验的标准试验方法),通过动态模量试验(dynamic modulus test)获取.基层及土基采用典型值.采用Prony级数和WLF方程实现黏弹性材料的时间依赖性和温度依赖性的定义[11].表4、表5和表6分别给出分析中所用的路面结构各层材料及参数.

表4　路面材料参数表(基准温度20 ℃)

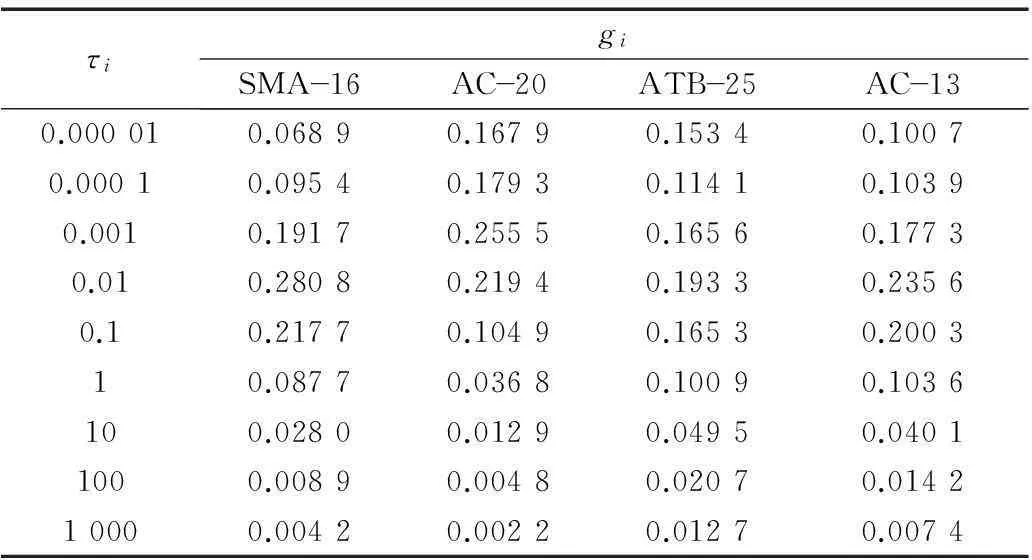
表5　沥青混合料Prony级数(基准温度20 ℃)

注：τi为延迟时间；gi为材料剪切常数

表6　Williams-Landel-Fer方程参数表

注：T0为参考温度；C1，C2为WLF方程回归常数

3实际温度场路面结构动力响应分析

3.1夏季低温时段各向应变

根据模拟结果，分析夏季低温时段路面结构在实际温度下的动力响应.提取横断面内各点的应变做等值线图，如图6所示.在横断面内，横向应变分布较为复杂.在荷载作用下方呈横向拉应变，在其他区域呈横向压应变.最大拉应变出现在中面层中下部，约为18×10-6.最大压应变出现在上面层底部，约为-22×10-6.荷载作用下方整个沥青层出现一定大小的横向拉应变，而横向压应变在中面层迅速减小到零.

在横断面内，竖向应变仅表现为竖向压应变，最大值出现在中面层中部，约为-95×10-6.在上面层出现纵向压应变，最大值在路表约为-12×10-6；在中下面层出现纵向拉应变，最大值在中面层下部，约为18×10-6.剪应变E23(图5中Y-Z平面)仅表现为负值，最大值出现在中面层底部，约为-43×10-6.

3.2夏季高温时段各向应变

图7所示为夏季高温时段路面结构横断面内各向应变等值线图.从图7可以看出，横向应变分布同夏季低温时段相似，但其值略大于夏季低温时段的应变值.竖向应变分布同夏季低温时段相似，表现为竖向压应变，但其值大于夏季低温时段的应变值.最大应变出现在中面层中部，约为-145×10-6，是夏季低温时段的1.53倍，竖向应变受温度影响较大.纵向应变和剪应变E23与夏季低温时段有相同分布规律，但最大响应为夏季低温时的1.39倍左右.

a 横向应变

b 竖向应变

c 纵向应变

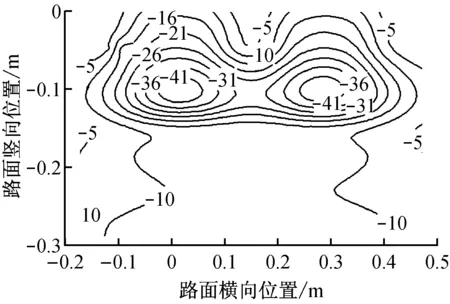
d 剪应变E23

a 横向应变

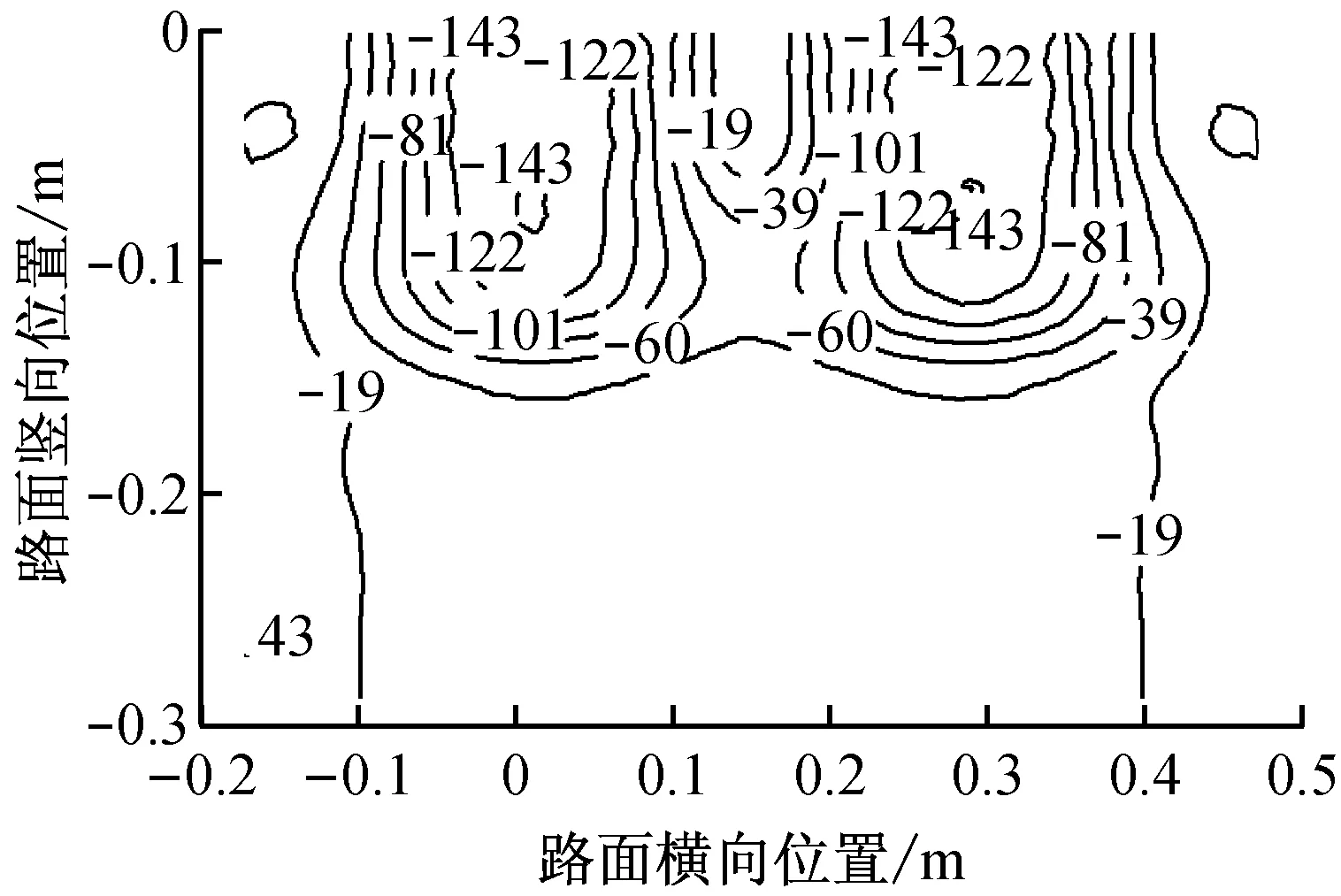
b 竖向应变

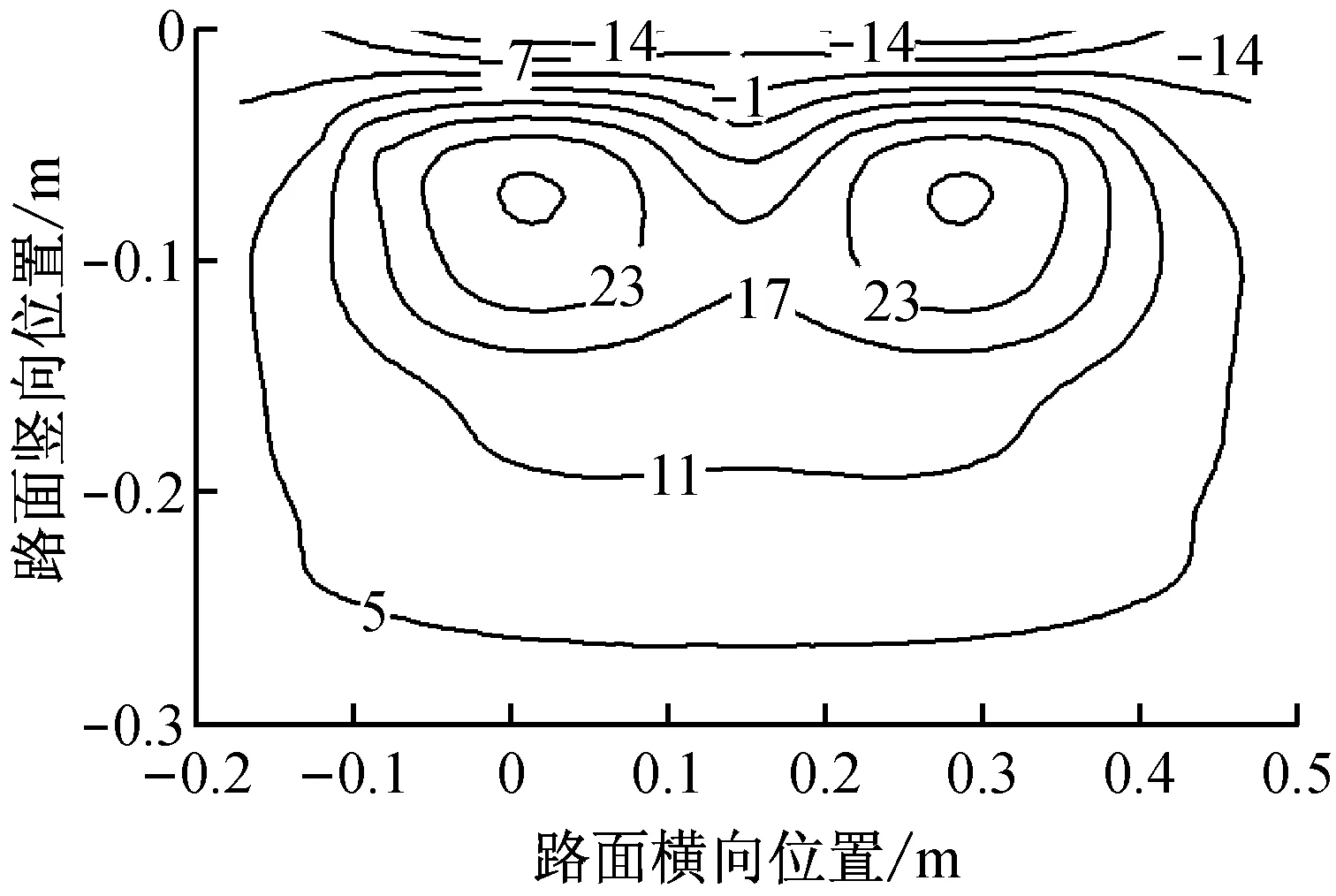
c 纵向应变

d 剪应变E23

图7夏季高温时段各向应变等值线图(单位：10-6)

Fig.7Contour of responses during high-temperature period in summer(unit: 10-6)

由以上分析可知，无论沥青路面结构在夏季高温时段呈正温度梯度分布，还是在低温时段呈负温度梯度分布，其路面结构的动力响应具有相似的分布规律，但温度场分布对竖向应变、纵向应变和剪应变E23值的影响较大，对横向应变值的影响较小.

4等温模型不足分析

4.1夏季低温时段响应对比分析

这里采用实际夏季低温时段模型的响应等值线图与25 ℃等温模型的响应等值线图做差，以分析夏季低温时段采用等温结构模型对沥青路面结构动力响应的影响，如图8所示.夏季低温时段采用等温模型计算的路面结构竖向应变小于实际竖向应变.路面上、下面层竖向应变的差值较小，在中面层竖向应变差值较大.这是因为在夏季低温时段，沥青层温度随深度增大而增大，沥青面层出现模量梯度(模量呈递减趋势)，路面中下面层出现较大竖向应变.

同时，夏季低温时段采用等温模型计算的路面结构剪应变小于实际剪应变，而剪应力基本相同.上中面层的剪应变差值较大，特别是在中面层，路面结构实际剪应变是等温模型的8倍.等温模型没有考虑夏季低温时段的负温度梯度，不能反映路面结构内的模量梯度，低估了温度对沥青层车辙及开裂的影响.

a 竖向应变差值(单位：10-6)

b 竖向应力差值(单位：kPa)

c 剪应变差值(单位：10-6)

d 剪应力差值(单位：kPa)

4.2夏季高温时段响应对比分析

为了分析夏季高温时段两种情况的差异，这里采用实际高温时段模型的响应等值线图与45 ℃等温模型的响应等值线图做差，如图9所示.在荷载作用及其影响区域，实际高温时段模型各点的竖向压应力略小于45 ℃等温模型的竖向压应力，而实际高温时段模型的竖向压应变小于45 ℃等温模型的值，且差值较大；在荷载作用区域实际高温时段模型与45 ℃等温模型的应变差值明显大于其他区域的差值，说明在荷载作用区域温度对路面结构有显著影响.与等温模型相比，夏季高温时段，沥青路面上面层存在正温度梯度，使沥青面层沿厚度方向产生模量梯度(模量呈递增趋势).等温结构模型不考虑温度梯度，不能反映路面材料的实际模量值和路面结构内的模量梯度，计算出的竖向应变大于实际值.

从图9中还可以看出，实际高温时段模型各点的剪应力与45 ℃等温模型的剪应力相差不大，但由于未考虑路面结构内的温度梯度，夏季高温时段等温模型不能真实反映温度对沥青层剪应变的影响.在上面层和下面层，等温模型计算的剪应变明显大于实际值.在中面层等温模型计算的剪应变值小于实际值，低估了温度对沥青路面中面层的影响.

a 竖向应变差值(单位：10-6)

b 竖向应力差值(单位：kPa)

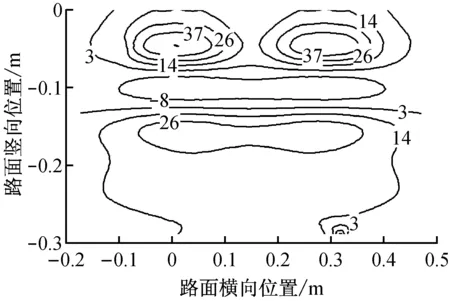
c 剪应变差值(单位：10-6)

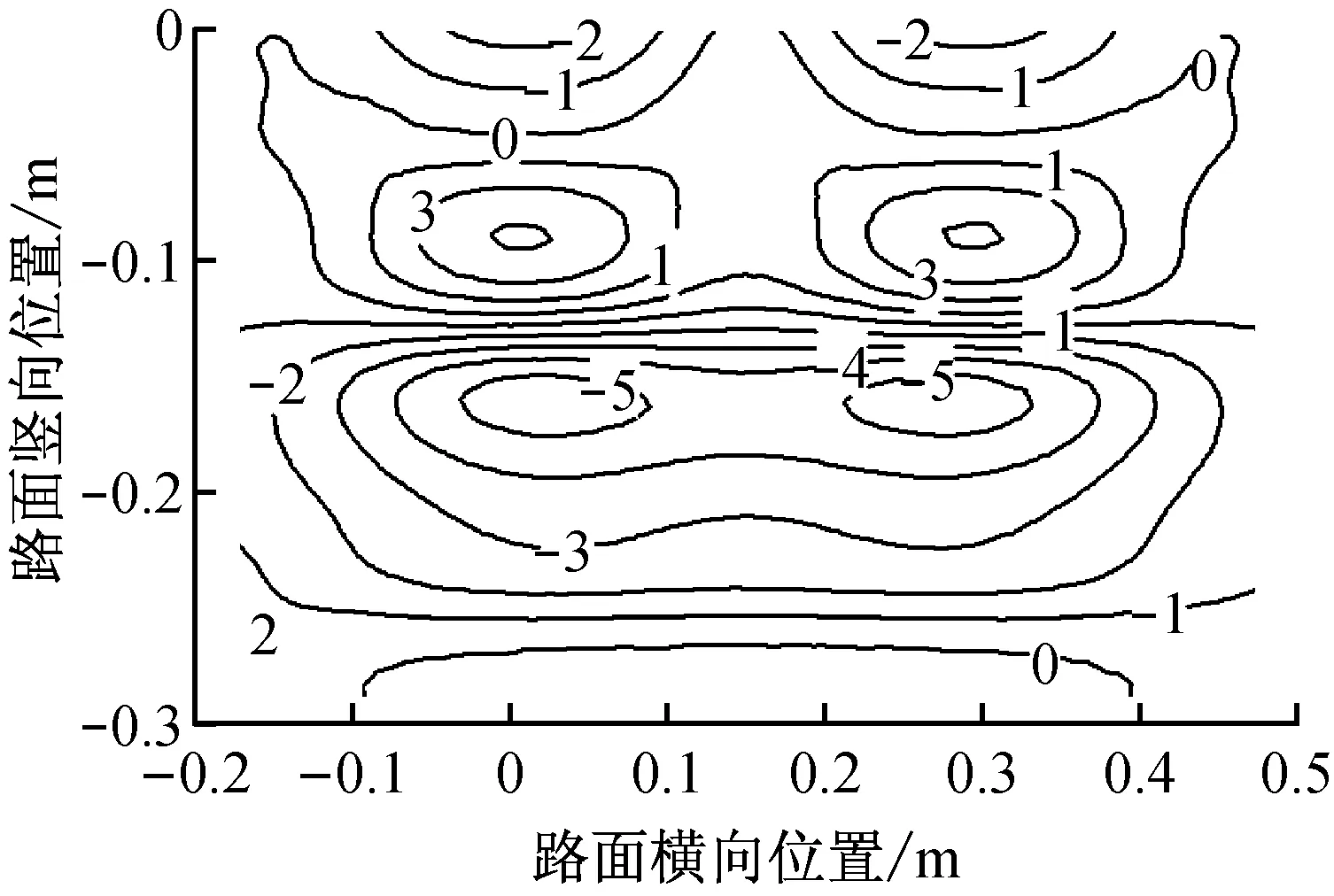
d 剪应力差值(单位：kPa)

5结论

基于温度场模拟和室内路面材料动态模量试验结果，建立非均布移动荷载作用下沥青路面瞬态动力分析三维有限元模型，对比分析处于实际温度场的沥青路面结构动力响应与等温路面结构的动力响应，得到以下结论：

(1) 层底控温方法模拟的沥青路面温度场具有一定的适用性.夏季高温时段及低温时段的模拟值和实测值比较接近，可以基于模拟的温度场分析夏季高温时段和夏季低温时段的路面结构实际动力响应.

(2)夏季高温时段和低温时段，沥青路面结构动力响应分布规律相似，但响应值不同.荷载对动力响应分布规律的影响大于温度梯度的影响，温度及温度梯度对响应的幅值有影响.

(3)夏季低温时段，沥青路面结构内存在负温度梯度.等温模型计算的竖向应变及剪应变小于实际值，低估了温度对沥青路面车辙及开裂的影响.

(4)夏季高温时段，等温模型不能反映沥青路面结构内的正温度梯度，高估了竖向应变及上、下面层的剪应变，低估了中面层的剪应变.因此,传统等温结构模型不能反映温度梯度交替变化对沥青路面结构动力响应的影响.

参考文献:

[1]CAO Liping, SUN Lijun, DONG Zejiao. Research on permanent deformation property of asphalt mixture with varying temperature[C]//Asphalt Material Characterization, Accelerated Testing, and Highway Management. Harbin: ICCTP, 2009: 32-38.

[2]孙立军. 沥青路面结构行为学[M]. 上海: 同济大学出版社, 2013.

SUN Lijun. Structural behavior study for asphalt pavements[M]. Shanghai: Tongji University Press, 2013.

[3]郑仲浪. 重载车辆作用下沥青路面层间力学行为研究[D]. 西安: 长安大学, 2010.

ZHENG Zhonglang. Mechanical behavior of the asphalt pavement interlayer under heavy vehicle[D]. Xi’an: Chang’an University, 2010.

[4]艾长发. 高寒地区沥青路面行为特性与设计方法研究[D]. 成都: 西南交通大学, 2008.

AI Changfa. Research of behavioral characteristics and design method of asphalt pavement at alpine region[D]. Chengdu: Southwest Jiaotong University, 2008.

[5]董忠红, 吕彭民. 移动荷载下倒装结构沥青路面动力响应[J]. 长安大学学报, 2008, 28(5): 111.

DONG Zhonghong, LV Pengmin. Dynamic response of flip asphalt pavement structure under moving loads[J]. Journal of Chang’an University, 2008, 28(5): 111.

[6]吕彭民. 温度对长大上坡路段沥青混凝土路面动力响应的影响[J]. 公路, 2013, 7(5): 14.

LV Pengmin. Temperature’s influence on the dynamic response of asphalt pavement in long uphill section[J]. Highway, 2013, 7(5): 14.

[7]Wang H, Al-Qadi I L. The combined effect of moving wheel loading and three-dimensional contact stresses on perpetual pavement responses[C]//Transportation Research Board 2009 Annual Meeting. Washington D C: TRB, 2009:1-14.

[8]李生龙. 沥青路面结构信息监测及疲劳性能预估[D]. 哈尔滨: 哈尔滨工业大学, 2013.

LI Shenglong. Information monitoring and performance prediction of asphalt pavement[D]. Harbin: Harbin Institute of Technology, 2013.

[9]贾璐, 孙立军, 黄立葵, 等. 沥青路面温度场数值预估模型[J]. 同济大学学报:自然科学版, 2007, 35(8): 1039.

JIA Lu, SUN Lijun, HUANG Likui,etal. A numerical temperature prediction model for asphalt concrete pavement[J]. Journal of Tongji University: Natural Science, 2007, 35(8): 1039.

[10]廖公云, 黄晓明. ABAQUS有限元软件在道路工程中的应用[M]. 南京: 东南大学出版社, 2008.

LIAO Gongyun, HUANG Xiaoming. Application of ABAQUS finite element software in road engineering[M]. Nanjing: Southeast University Press, 2008.

[11]董泽蛟, 谭忆秋, 欧进萍. 三向非均布移动荷载作用下沥青路面动力响应分析[J]. 土木工程学报, 2013, 46(6): 122.

DONG Zejiao, TAN Yiqiu, OU Jinping. Dynamic response analysis of asphalt pavement subjected to three-directional non-uniform moving load[J]. China Civil Engineering Journal, 2013, 46(6): 122.

Dynamic Response Analysis of Asphalt Pavement Due to Combined Non-Uniform Moving Load and Temperature Distribution

DONG Zejiao1， PAN Xiaokang1,2， SHAO Xianzhi3， ZHOU Xingye4

(1. School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin 150090, China; 2. National Engineering Research Center of Road Maintenance Technologies, Beijing 100095, China; 3. China Airport Construction Group Corporation, Beijing 100100, China; 4. Research Institute of Highway, Ministry of Transport, Beijing 100088, China)

Abstract：To study the influence of temperature distribution on the dynamic response of asphalt pavement, a 3D finite element model in transient mode of asphalt pavement, subjected to non-uniform moving load, was established based on the measured temperature distribution in the field and the dynamic modulus results of the actual pavement material in lab. The dynamic response time history and spatial distribution of pavement structure within the actual temperature field was analyzed and compared with that of the isothermal structure model. The result shows that the temperature simulated by the bottom temperature control method could be used to analyze the actual dynamic response during both the low-temperature and high-temperature period in summer. The isothermal pavement structure overestimates the vertical strain and the shear strain of upper layer and lower layer, but underestimates the shear strain of the middle layer during the high-temperature period in summer. During the low-temperature period in summer, the actual dynamic response of asphalt pavement was larger than the value calculated from the isothermal model. The isothermal model underestimates the effect of temperature distribution on the rutting and cracking potential of asphalt pavement.

Key words：road engineering; isothermal model; numerical simulation; dynamic response; temperature field; non-uniform moving load

收稿日期：2015-03-27

基金项目：国家自然科学基金(51278159，51478154)

中图分类号：U416.2

文献标志码：A

第一作者： 董泽蛟(1979—)，男，教授，博士生导师，工学博士，主要研究方向为路面计算力学及信息监测. E-mail: hitdzj@hit.edu.cn