孔隙填充型深海能源土的离散元成样新方法及宏观力学特性

贺　洁，　蒋明镜

(1. 同济大学 土木工程防灾国家重点实验室， 上海 200092； 2. 同济大学 岩土及地下工程教育部重点实验室， 上海 200092)



孔隙填充型深海能源土的离散元成样新方法及宏观力学特性

贺洁1, 2，蒋明镜1, 2

(1. 同济大学 土木工程防灾国家重点实验室， 上海 200092； 2. 同济大学 岩土及地下工程教育部重点实验室， 上海 200092)

摘要：针对孔隙填充型水合物的赋存形态，提出了一种新的制备孔隙填充型能源土试样的数值成样方法.孔隙填充型水合物的砂性能源土试样是由砂粒和水合物颗粒混合而成的特殊的散粒体材料，具有明显的非连续特征.在土骨架的孔隙中，将水合物块体视为由颗粒通过强胶结作用凝聚而成的团簇整体，随机填充生成不同水合物饱和度的沉积物试样，开展能源土宏观力学特性的离散元固结排水三轴压缩试验模拟，并从应力应变、体变、接触组构等方面进行分析.结果表明，水合物饱和度的增大对低饱和度的孔隙填充型能源土试样的初始弹性模量和强度影响较小.有效围压相同时，孔隙填充型能源土试样的体积剪缩量随着水合物饱和度的增大而减小；而水合物饱和度相同时，能源土试样强度及体积剪缩量随着有效围压的增大而增大.能源土试样的剪胀角随有效围压的增大而近似线性减少，随水合物饱和度的增大而趋于线性增大.颗粒间接触方向随着轴向应变的增大而朝竖直方向偏转.

关键词：离散单元法； 孔隙填充型能源土； 数值生成方法； 水合物饱和度； 力学特性； 接触组构

作为一种新能源，天然气水合物含碳总量巨大，具有极为广阔的发展前景，已经引起世界上许多国家的关注.美国，加拿大，日本，中国等相继开展了本土和国际海底天然气水合物的调研工作，并制定了勘查和开发天然气水合物的国家计划[1-2].然而水合物的商业开采，将会引起沉积物抗剪强度的降低、孔隙水压的增加、渗透性能的改变等问题，可能诱发一系列岩土工程问题，如海底滑坡、海洋钻井平台地基变形及水合物勘探平台的倒塌等[3].

作为一种新型的岩土材料，水合物沉积物具有比传统岩土材料更为复杂的物质组成，通常由土体颗粒、水、气体和天然气水合物组成，其力学性质与各组成成分的性质和状态密切相关，各组分之间的相互作用决定了其力学表现，其中，固体水合物与土体颗粒之间的相互作用影响最大[4].很明显，水合物在孔隙中的存在形式不同，其与土体骨架的作用也就不一样，从而导致水合物沉积物表现出不同的力学特性.因此，在深入分析天然气水合物沉积物的力学特性之前，有必要了解天然气水合物在沉积物中的存在形式及状态.尽管不同学者[2, 5-9]对水合物在沉积物中的微观分布形式划分有细微的差别，但在一定程度上得到了较为统一的结论，即胶结型水合物沉积物和孔隙填充型水合物沉积物两种主要赋存形态.天然气水合物在世界范围内以不同微观分布形式广泛地存在，东北太平洋水合物海岭等地存在胶结型的水合物沉积物；而南海海槽、麦肯齐三角洲、布莱克海岭等地发现了孔隙填充型的水合物沉积[2].

国内外学者[10-14]在室内通过不同制样方法合成了能源土试样，研究水合物形成机制及成核地点对水合物沉积物特性的影响.此外，许多学者采用离散单元数值方法(distinct element method, DEM)[15]，从微观结构出发，直接生成不同微观分布形态的能源土试样，研究颗粒集合体在不同加载情况下的宏微观响应，开展了一些卓有成效的数值模拟.蒋明镜等[16-17]建立了反映能源土颗粒间水合物力学特性的微观胶结模型，将模型程序化并引入离散元单元法中，研究胶结型水合物对能源土力学性质的影响.伦敦大学学院Helen Cheng团队通过在土颗粒的孔隙中随机生成定量的球形水合物颗粒研究了含填充型水合物的能源土试样的力学特性[18-19].

孔隙填充型水合物的砂性能源土试样是由砂粒和水合物颗粒混合而成的特殊的散粒体材料，具有明显的非连续特征.为实现此类型的水合物沉积试样力学和变形特性的离散元模拟，需要一种可重复性的数值试样制备方法.本文借鉴Brugada等[18]提出的填充型成样方法，并基于之前已经取得的甲烷水合物不同加荷模式的离散元力学特性模拟成果[20-21]，提出一种新的制备孔隙填充型水合物沉积物的数值制备方法，即孔隙填充水合物生成技术.首先，详细阐述了离散元中孔隙填充水合物生成技术的理论推导和实现方法，即将水合物块体视为由颗粒胶结作用凝聚而成的团簇整体，在土颗粒的孔隙中随机填充并生成相应水合物饱和度的能源土试样；其次，基于先前甲烷水合物单轴压缩试验模拟结果[21]，确定水合物团簇间的胶结模型参数取值；随后，对不同水合物饱和度的能源土试样开展了三轴压缩试验的离散元模拟，探讨成样方法的可行性及孔隙填充型能源土样的力学和变形特性.

1孔隙填充型能源土试样实现

天然气水合物赋存条件相当苛刻(适宜的高压、低温条件)，从深海海底采取原状试样，对技术要求极高、费用也极其昂贵.采用原状能源土试样进行相关力学性能研究存在极大限制，为此，目前对水合物沉积物试验的研究大多数采用室内合成试样.这些研究加深了对水合物沉积物力学特性的认识.然而，由于技术限制，室内试验无法对影响水合物沉积物力学特性的诸多因素进行单独探究，难以揭示复杂宏观现象的微观机理，必定影响其本构理论的建立.故而，本文针对水合物在沉积物中的赋存形态，提出一种新的孔隙填充型水合物沉积物的离散元制备方法，以实现孔隙填充型的能源土试样的离散元模拟和力学特性分析.

1.1土试样制备

采用Jiang等[22]提出的分层欠压法(UCM法)生成初始孔隙比为0.84，长、宽、高分别为3.704，3.704，7.408 mm的长方体试样，如图1所示.为使离散元模拟更好地符合真实情况，采用图2所示粒径级配.模拟土颗粒的圆球颗粒直径为0.10～0.42 mm，与Toyoura砂粒径接近，试样中土颗粒数目设置为10 000.

图1　三维离散元土颗粒试样

图2　离散元模拟和室内试验Toyoura砂的颗粒级配曲线

Fig.2Particle size distribution used in DEM simulation and Toyoura sand in laboratory test

1.2水合物颗粒填充

水合物饱和度是指水合物体积占孔隙体积的百分比.即

(1)

式中：Vmh为水合物体积；Vv为孔隙体积.

试样的孔隙体积Vv可由试样的总体积及成样后的孔隙比计算得到.即

(2)

式中：V为试样的体积，可根据长方体试样的长宽高计算得到；L，W，H分别为长方体试样的长、宽、高；e为分层欠压法成样完成后试样的孔隙比.

Brugada等[18]在研究孔隙填充型水合物的沉积物力学性质时，随机在土颗粒的孔隙中生成了定量的球形水合物颗粒，其水合物颗粒数目的具体求解过程如下：

土骨架的孔隙体积Vv由公式(2)求得后，设定填充水合物颗粒的单一半径，根据公式(1)即可推算出形成特定饱和度的沉积物试样所需填充的水合物颗粒数目N′.即

(3)

式中：N′为指定水合物饱和度的试样中需要填充的水合物颗粒数目；R为水合物颗粒的半径.

Brugada等[18]根据公式(3)确定了不同水合物饱和度的水合物沉积物试样所需填充的颗粒数目，随机在土颗粒的孔隙中生成相应数目的水合物颗粒，研究了水合物饱和度对孔隙填充型水合物的能源土试样力学性质的影响.然而，这种做法，一方面无法确保填充到土颗粒的颗粒确实能够反映水合物本身的力学特性；另一方面，用离散的、不能破坏的小颗粒模拟水合物，忽略了水合物破坏对沉积物力学性质产生的影响，与实际情况存在一定的差异.为了能模拟沉积物中水合物的破坏，本文在Brugada等[18]成样方法的基础上进行了改进，使单个水合物颗粒通过胶结作用胶结在一起，生成水合物团簇，开展不同饱和度的水合物沉积物试样的力学和变形特性研究.

图3给出了单水合物团簇的示意图，在以球体半径为Ra的范围内生成单一颗粒半径为r的水合物小颗粒，然后通过强胶结作用将这些水合物颗粒凝聚而成为整体，合理确定颗粒间胶结模型参数，使其达到反压的效果.如图3所示，浅色线条表示颗粒间的胶结作用.在这个过程中，控制参量为球体的半径Ra，即水合物团簇的等效半径Ra和孔隙比ea.

由水合物团簇孔隙比ea的定义可推导求得水合物团簇的等效半径Ra.具体过程如下：首先，由孔隙比的概念可知

(4)

式中：r为水合物团簇中颗粒的半径；n为一个水合物团簇中的颗粒数目.

随之，根据公式(4)，可推导出水合物团簇的等效半径Ra的求解公式，即

(5)

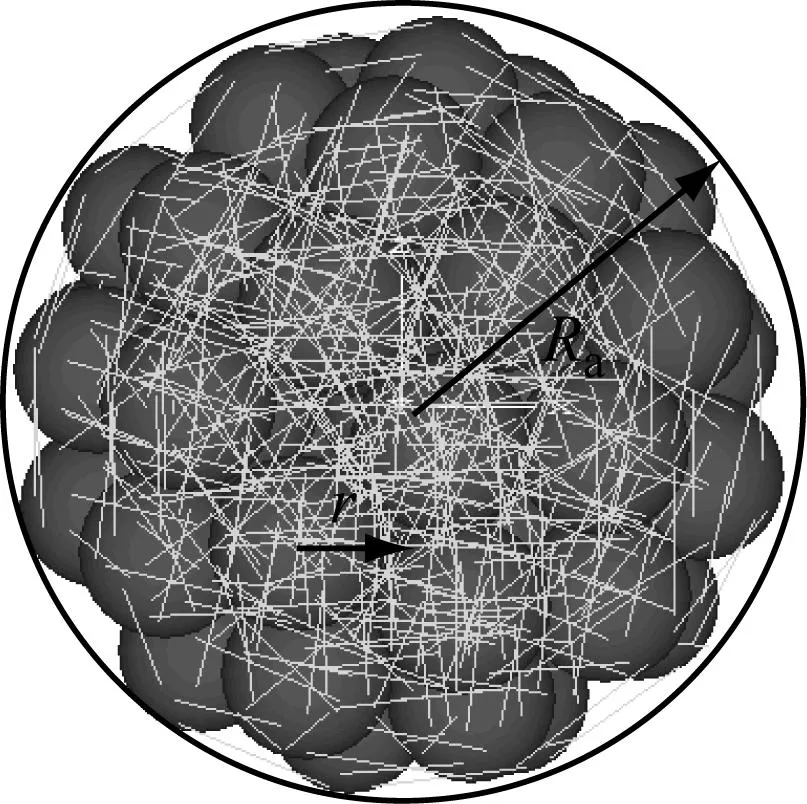
图3　单水合物团簇示意图

水合物团簇内颗粒间是有一定孔隙的，因此将水合物团簇作为一个整体来分析的时候，不应该仅仅计算团簇内颗粒的体积.根据土力学孔隙比的概念，存在如下等式关系：

(6)

式中：Va表示单个水合物团簇的体积.

进一步化简求得Va的表达式为

(7)

确定孔隙填充型水合物的沉积物试样中需要填充的水合物团簇的数目，使其达到目标饱和度.水合物沉积物试样中存在如下的等式关系：

Vmh=NVa

(8)

式中：N表示特定水合物饱和度试样中水合物团簇的数目.

故而，需要填充的水合物团簇的数目为

(9)

根据以上理论推导，在土试样中形成水合物团簇的具体过程如下：

(1) 在土试样中随机生成半径为Ra的圆球颗粒，颗粒数目为N，即水合物团簇的颗粒数目.循环10 000步，使颗粒达到平衡状态，完成后的试样如图4a所示，填充到土颗粒孔隙中的圆球颗粒用深色突出显示.

(2) 删除圆球颗粒，且在圆球范围内生成n个单一粒径r的小颗粒，然后通过强胶结作用将这些水合物颗粒凝聚而成为水合物团簇，如图4b所示.离散元模拟的基本参数如下:土颗粒密度为2.65 g·cm-3,水合物密度为0.9 g·cm-3,初始孔隙比为0.84,土颗粒法向刚度为1.5×106N·m-1,土颗粒切向刚度为1.0×106N·m-1,土粒间摩擦系数为0.5,墙体法向刚度为1.5×106N·m-1,墙体法向刚度为1.0×106N·m-1,水合物法向刚度为1.5×106N·m-1,水合物切向刚度为1.0×106N·m-1,水合物粒间摩擦系数为0.04.在离散元固结排水三轴压缩试验的模拟中，颗粒的密度值的选取不会影响计算结果.本文土颗粒密度和水合物密度分别取为2.65和0.90 g·cm-3，是因为这两个数值与实际情况相符合.而在Jung等[23]开展的水合物沉积物离散元模拟中，土颗粒密度和水合物密度均取为2.65 g·cm-3.此外颗粒间摩擦系数的选取主要影响试样的宏观强度值，对宏观刚度值影响较小.文献[18]中指出水合物颗粒和土颗粒刚度比取值仍需要进一步研究，本文借鉴不同学者[18, 23-24]对水合物沉积物力学性质研究中的参数取值，将土颗粒和水合物颗粒的法向接触刚度均设置为1.5×106N·m-1.

a土颗粒孔隙中填充水合物颗粒b水合物颗粒胶结形成水合物团簇

图4孔隙填充型水合物三维离散元试样

Fig.4Three dimensional distinct element specimen of

pore-filling type of MHBS

2离散元模拟参数选取

Potyond等[25]介绍了离散元中的两种胶结模型，接触胶结模型(contact-bond model)和平行胶结模型(parallel-bond model)，前者假设胶结只发生在接触点处，胶结面积非常小，故而接触胶结只能传递力；而平行胶结模型认为在两接触颗粒间存在一定的环形断面内均有胶结作用，胶结面积大小通过命令控制，该胶结能同时传递力和力矩.

孔隙填充型水合物的能源土试样中，水合物团簇视为由离散元圆球小颗粒通过强胶结作用凝聚而成的整体，接触处的颗粒相对运动时在胶结物内能同时产生力和力矩.本文选用平行胶结模型来模拟胶结物的力学特性.为了文章的完整性，简要介绍平行胶结模型的力学特性和破坏准则，读者也可查阅离散元商业软件PFC3D用户手册[26].

(10)

(11)

(12)

图5　平行胶结模型胶结物传递的力和力矩

(13)

(14)

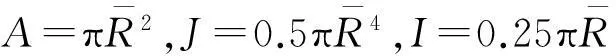
参考文献[20]，采用三维离散元数值方法模拟了甲烷水合物三轴压缩试验，并与已有室内试验成果[24, 27]对比，实现了高水压、低温条件下的甲烷水合物材料的宏观强度和变形特性的模拟.随后，为提出孔隙填充水合物生成技术，蒋明镜等[21]详细阐述了采用离散元单轴压缩试验思路，将室内试验中的内部孔隙水压作用转化为水合物颗粒间的胶结力，通过参数反演建立了宏观强度、刚度参数与平行胶结模型的微观胶结参数间的宏微观关系；离散元单轴压缩试验较好地模拟了室内三轴试验的宏观强度特性，实现不同加荷模式下甲烷水合物的离散元模拟.

为了在土试样中实现不同水合物饱和度的水合物团簇的填充，使得填充的单团簇集合体能符合水合物本身的力学特性，首先需要确定单团簇中颗粒的数目n.Cheng等[28]在进行砂土的破碎演化研究时，单团簇中颗粒数目范围为41～57.本文采用60个小颗粒生成水合物团簇；单一水合物团簇的生成具体步骤如下：

(1) 求解水合物团簇的等效半径Ra.为使得模拟计算结果更加可靠，参考文献[21]，控制水合物团簇的孔隙比为0.82，生成60个单一粒径为0.024 mm的颗粒.由公式(5)求得等效半径Ra约为0.114 mm.

(2) 以原点为球心，Ra为半径的球体范围，生成球体墙和上下两道水平墙体.

(3) 在球体墙内，生成60个单一粒径为0.024 mm的颗粒.需要说明的是，为在球体范围内顺利实现颗粒填充，首先生成0.02 mm的小颗粒，然后将所有颗粒粒径给予1.2倍的放大系数，生成0.024 mm的颗粒.颗粒填充完成后，循环10 000步，监测颗粒间的接触力，控制颗粒间的重叠量在合理范围内，使其达到初始平衡状态.

3离散元模拟分析

根据之前不同学者[29-31]所做的研究，在固体沉积物中，水合物先在孔隙中形成，随后逐渐向土体骨架靠拢，在沉积物颗粒间形成胶结；孔隙填充型水合物沉积物主要在低水合物饱和度情况下生成.采用前文所述孔隙填充型水合物沉积物试样的成样方法，选择3个较低的水合物饱和度，即Smh=5%，10%，15%，由公式(9)获得相应水合物饱和度试样所需填充的水合物团簇的数目分别为614，1 228，1 842；随后，模拟室内固结排水三轴压缩试验，研究孔隙填充型水合物沉积物的宏微观力学特性.

3.1应力应变关系

图6给出了2 MPa围压时不同水合物饱和度下(Smh=5%，10%，15%)，孔隙填充型能源土试样的应力应变关系.由图6可知，水合物沉积物试样的初始弹性模量随着水合物饱和度的增大而逐渐增大，但是增大趋势并不很明显.正如Clayton等[29]和Kingston等[30]的研究，只有水合物饱和度大于20%时才会对砂样的弹性模量有较显著的影响.随着水合物饱和度的增加，偏应力随着轴向应变的增大而逐渐增大，然而增大趋势并不显著.图7给出Hyodo等[31]在室内温度5 ℃，有效围压5 MPa时水合物沉积物试样的三轴压缩试验的应力应变关系曲线.由图7可知，水合物饱和度由Smh=0增大到Smh=24.2%时，水合物沉积物试样的偏应力强度值变化较小.由以上分析可知，孔隙填充型水合物沉积物试样的初始弹性模量和偏应力强度会随着水合物饱和的增大而略微增大.

图6　不同Smh孔隙填充型能源土试样的应力应变关系

Fig.6Deviator stress-axial strain relationship under different MH saturations for pore-filling type of MHBS

图7Hyodo等[31]不同Smh能源土试样三轴压缩试验的应力应变关系曲线

Fig.7Deviator stress-axial strain relationship of different MH saturations of MHBS obtained from the triaxial compression tests conducted by Hyodoetal.[30]

图8给出了不同水合物饱和度的能源土试样在不同有效围压下的应力应变关系曲线.由图8可知，在同一Smh值下，能源土试样的偏应力随着有效围压的增大而增大.

根据图8给出的不同有效围压时的深海能源土三轴压缩试验的应力应变关系，从而可求得不同水合物饱和度Smh的能源土试样的强度参数内摩擦角和黏聚力，如图9所示.孔隙填充型能源土试样的内摩擦角φ随着水合物饱和度的增大而近似线性增大；然而，随着水合物饱和度的增大，孔隙填充型能源土试样的黏聚力c先增大后减小，黏聚力c的变化趋势并不明朗，这与Brugada等[18]所开展的孔隙填充型能源土特性相符合，即对于孔隙填充型能源土试样，水合物对于试样力学特性的贡献主要是摩擦特性而非胶结特性.

a Smh= 5%

b Smh= 10%

c Smh= 15%

Fig.8Deviator stress-axial strain relationship under different effective confining pressure for pore-filling type of MHBS with different MH saturations

3.2体变关系

图10给出了不同水合物饱和度下，孔隙填充型水合物沉积物试样的体变关系.由图10可知，水合物饱和度从Smh=0增大到Smh=10%时，水合物沉积物试样的体积剪缩量变化不大，但是总的趋势看来，随着水合物饱和度的增大试样的体积剪缩量减小，水合物饱和度Smh=15%的能源土试样的体积剪缩量最小.在相同的土骨架中填充不同体积的水合物团簇，所填充的团簇数目越多，土骨架中的孔隙就会越少，进而在模拟三轴压缩试样时，水合物饱和度大的能源土试样的体积剪缩量会偏小.随着轴向应变的发展，水合物团簇中的胶结会逐渐破坏，土颗粒和水合物颗粒通过颗粒间的挤压和错动来调整所处位置，从而水合物沉积物试样表现出体胀现象.

图9　能源土试样的内摩擦角和黏聚力随水合物饱和

Fig.9MHBS internal friction angle and cohesion at variation of MH saturations

图10　不同Smh的孔隙填充型能源土试样的体变规律

Fig.10Volumetric-axial strain relationship under different MH saturations for pore-filling type of MHBS

图11分别给出了不同水合物饱和度的能源土试样在不同有效围压下的体变关系曲线.由图11可知，在同一Smh值下，能源土试样的体缩量随着有效围压的增大而更加明显.

基于以上给出的不同水合物饱和度的能源土试样的体变关系，图12给出了剪胀角正弦值随不同有效围压和水合物饱和度的变化规律.由Roscoe[32]提出的剪胀角ψ的计算公式如下:

(15)

由图12可知，在相同水合物饱和度Smh下，能源土试样的剪胀角ψ随有效围压增大近似线性减少；类似地，在相同有效围压作用下，能源土试样的剪胀角ψ随水合物饱和度Smh增大趋于线性增大.

3.3接触组构

颗粒接触点有2个接触方向，如图13所示，n和-n为单位接触方向矢量，用φ和θ定义n.

a Smh= 5%

b Smh= 10%

c Smh= 15%

Fig.11Volumetric-axial strain relationship under different confining pressures for pore-filling type of MHBS with different MH saturations

Oda等[33]给出了二阶接触组构张量的计算公式(16)，当主对角线的F11，F22和F33相等时代表接触方向在空间分布各向同性；某一值偏大，表示接触方向倾向于该方向分布.

(16)

a 剪胀角与有效围压关系

b 剪胀角与水合物饱和度关系

Fig.12Shear dilatancy angle with changes of effective confining pressures and MH saturations

图13　n向量的表示

图14给出水合物饱和度Smh=5%时，不同轴向应变值εa=0.91%，5.58%，17.1%下，能源土试样的接触方向组构分布图.由图14可知，颗粒间接触方向随着轴向应变的增大而朝竖直方向偏转.

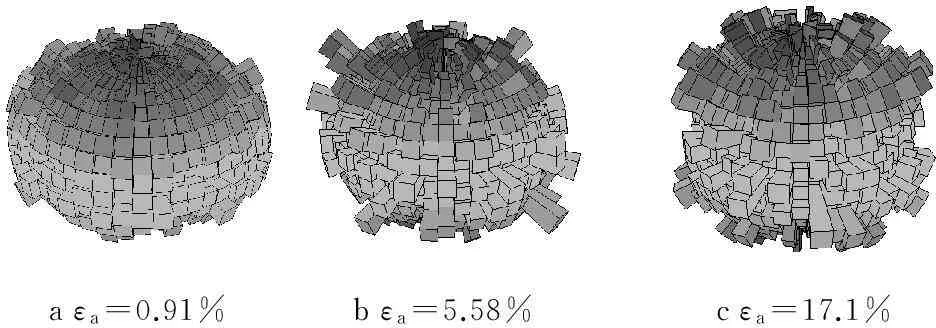
aεa=0.91%bεa=5.58%cεa=17.1%

图14不同轴向应变值对应的接触方向组构分布

Fig.14Contact directions distribution at different

axial strains

4结论

孔隙填充型水合物的能源土试样可视为砂粒和水合物颗粒混合物，具有明显的非连续特征.本文在前人研究基础上，提出了一种新的孔隙填充型水合物沉积物试样的离散元数值制备方法.随后，采用该方法生成了3个低水合物饱和度的能源土试样(Smh=5%，10%，15%)，通过模拟三轴压缩试验来研究孔隙填充型水合物沉积物的宏微观力学特性.主要结论如下：

(1) 水合物饱和度的增大对低饱和度的孔隙填充型的能源土试样的初始弹性模量和强度影响较小.孔隙填充型水合物的沉积物试样的体积剪缩量随着水合物饱和度的增大而减小.

(2) 水合物沉积物试样的初始弹性模量和偏应力随着有效围压的增大而明显增大.有效围压越大，体积收缩量越大；而剪胀特性随着有效围压的减小而呈现增强趋势.能源土试样的剪胀角随有效围压的增大而近似线性减少，随水合物饱和度的增大而趋于线性增大.

(3) 随着轴向应变的增大，颗粒间接触方向朝竖直方向偏转.

参考文献:

[1]National Research Council of the National Academies. Realizing the energy potential of methane hydrate for the United States [M]. Washington D C: The National Academies Press, 2010.

[2]Soga K, Lee S L, Ng M Y A,etal. Characterisation and engineering properties of methane hydrate soils [C]∥The 2th International Workshop on Characterisation and Engineering Properties of Natural Soils. Singapore: Taylor and Francis, 2007, 4: 2591-2642.

[3]Nixon M F, Grozic J L H. Submarine slope failure due to hydrate dissociation: a preliminary quantification [J]. Canadian Geotechnical Journal, 2007, 44(3): 314.

[4]Yamamoto K. Methane hydrate bearing sediments: a new subject of geomechanics [C]∥The 12th International Conference of International Association for Computer Methods and Advances in Geomechanics (IACMAG). Goa: [s.n.], 2008: 1188-1196.

[5]Holland M, Schultheiss P, Roberts J,etal. Observed gas hydrate morphologies in marine sediments [C/CD]∥The 6th International Conference on Gas Hydrates. Vancouver: [s. n.], 2008: 1-7.

[6]Dai J C, Snyder F, Gillespie D,etal. Exploration for gas hydrates in the deep water, northern Gulf of Mexico: Part I. A seismic approach based on geologic model, inversion, and rock physics principles [J]. Marine and Petroleum Geology, 2008, 25(9): 830.

[7]Dvorkin J, Helgerud M B, Waite W F,etal. Introduction to physical properties and elasticity models [C]∥Natural Gas Hydrate in Oceanic and Permafrost Environments. Dordrecht: Kluwer Academic Publishers, 2000: 245-260.

[8]Uchida S, Soga K, Yamamoto K. Critical state soil constitutive model for methane hydrate soil [J]. Journal of Geophysical Research, 2012, 117(B3): B03209.

[9]Waite W F, Santamarina J C, Cortes D D,etal. Physical properties of hydrate-bearing sediments[J]. Reviews of Geophysics, 2009, 47(4): RG4003.

[10]张旭辉, 王淑云, 李清平, 等. 天然气水合物沉积物力学性质试验研究[J]. 岩土力学, 2010, 31(10): 3069.

ZHANG Xuhui, WANG Shuyun, LI Qingping,etal. Experimental study of mechanical properties of gas hydrate deposits [J]. Rock and Soil Mechanics, 2011, 31(10): 3069.

[11]颜荣涛，韦昌富，魏厚振，等. 水合物形成对含水合物砂土强度影响[J]. 岩土工程学报, 2012, 34(7): 1234.

YAN Rongtao, WEI Changfu, WEI Houzhen,etal. Effect of hydrate formation on mechanical strength of hydrate-bearing sand[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(7): 1234.

[12]Masui A, Haneda H, Ogata Y O,etal. The effect of saturation degree of methane hydrate on the shear strength of synthetic methane hydrate sediments [C]∥The 5th International Conference on Gas Hydrate. Trondheim: Tapir Academic Press, 2005: 657-663.

[13]Winters W J, Pecher I A, Waite W F,etal. Physical properties and rock physics models of sediment containing natural and laboratory-formed methane gas hydrate [J]. American Mineralogist, 2004, 89(8-9): 1221.

[14]Ghiassian H, Grozic J L H. Methane hydrate formation under controlled pressure in the triaxial apparatus [C]∥63rd Canadian Geotechnical Conference & 6th Canadian Permafrost Conference. Calgary: [s. n.], 2010: 1548-1554.

[15]Cundall P A, Strack O D L. The discrete numerical model for granular assemblies [J]. Géotechnique, 1979, 29(1): 47.

[16]Jiang M J, Sun Y G, Yang Q J. A simple distinct element modeling of the mechanical behavior of methane hydrate-bearing sediments in deep seabed [J]. Granular Matter, 2013, 15(2): 209.

[17]蒋明镜, 贺洁, 周雅萍. 基于微观胶结厚度模型的深海能源土宏观力学特性离散元分析[J]. 岩土力学, 2013, 34(9): 2672.

JIANG Mingjing, HE Jie, ZHOU Yaping. Distinct element analysis of macro-mechanical properties of deep-sea methane hydrate-bearing soil using micro-bond thickness model[J]. Rock and Soil Mechanics, 2013, 34(9): 2672.

[18]Brugada J, Cheng Y P, Soga K,etal. Discrete element modelling of geomechanical behaviour of methane hydrate soils with pore-filling hydrate distribution [J]. Granular Matter, 2010, 12(5): 517.

[19]Yu Y, Cheng Y P, Soga K. Mechanical behaviour of methane hydrate soil sediments using discrete element method: pore-filling hydrate distribution [C]∥Discrete Element Modelling of Particulate Media. Birmingham:[s.n.], 2012: 264-270.

[20]蒋明镜，贺洁，申志福. 甲烷水合物三维离散元模拟参数反演初探[J]. 岩土工程学报, 2014, 36(4): 736.

JIANG Mingjing, HE Jie, SHEN Zhifu. Preliminary investigation on parametric inversion for three-dimensional distinct element modeling of methane hydrate[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(4): 736.

[21]蒋明镜, 贺洁. 三维离散元单轴试验模拟甲烷水合物宏观三轴强度特性[J]. 岩土力学, 2014, 35(9): 2692.

JIANG Mingjing, HE Jie. Three-dimensional distinct element simulation of macro triaxial compressional strength characteristics of methane hydrate through uniaxial compressional test [J]. Rock and Soil Mechanics, 2014, 35(9): 2692.

[22]Jiang M J, Konrad J M, Leroueil S. An efficient technique for generating homogeneous specimens for DEM studies [J]. Computers and Geotechnics, 2003, 30(7): 579.

[23]Jung J W, Santamarina J C, Soga K. Stress-strain response of hydrate-bearing sands: numerical study using discrete element method simulations[J]. Journal of Geophysical Research：Solid Earth, 2012，117(B04): B04202.

[24]Hyodo M, Nakata Y, Yoshimoto N,etal. Basic research on the mechanical behavior of methane hydrate-sediments mixture[J]. Japanese Geotechnical Society, 2005, 45(1): 75.

[25]Potyondy D, Cundall P. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1329.

[26]Itasca Consulting Group Inc. Particle flow code in 3 dimensions: version 3.0[R]. Minneapolis: Itasca Consulting Group, 2002.

[27]Nabeshima Y, Takai Y. Compressive strength and density of methane hydrate[C]∥The 6th ISOPE Ocean Mining Symposium. [S.l.]: International Society of Offshore and Polar Engineers, 2005: 199-202.

[28]Cheng Y P, Nakata Y, Bolton M D. Discrete element simulation of crushable soil [J]. Géotechnique, 2003, 53(7): 633.

[29]Clayton C R I, Priest J A, Rees E V L. The effects of hydrate cement on the stiffness of some sands [J]. Géotechnique, 2010, 60(6): 435.

[30]Kingston E, Clayton C, Priest J. Gas hydrate growth morphologies and their effect on the stiffness and damping of a hydrate bearing sand [C]∥The 6th International Conference on Gas Hydrates (ICGH 2008). Vancouver: [s. n.], 2008: 1-8.

[31]Hyodo M, Yoneda J, Yoshimoto N,etal. Mechanical and dissociation properties of methane hydrate-bearing sand in deep seabed[J]. Soils and Foundations, 2013, 53(2): 299.

[32]Roscoe K. The influence of strains in soil mechanics[J]. Geotechnique, 1970, 20(2): 129.

[33]Oda M, Iwashita K. Mechanics of granular materials[M]. Amsterdam: A A Balkema, 1999.

Three-Dimensional Distinct Element Novel Sample-Preparing Method and Mechanical Behavior for Pore-Filling Type of Methane Hydrate-Bearing Soil

HE Jie1,2, JIANG Mingjing1,2

(1. State Key Laboratory Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China; 2. Key Laboratory of Geotechnical and Underground Engineering of the Ministry of Education, Tongji University, Shanghai, China)

Abstract：In view of the morphology of pore-filling type of methane hydrate-bearing sediment (MHBS), this paper proposed a new technique for generating pore-filling type of MHBS. Marine sandy sediments containing pore-filling type MH particles can be considered as a class of special granular materials that present apparent obvious discontinuity characteristics. To numerically simulate such materials, the distinct element method (DEM) can be used by modeling MH particles as agglomerates of spheres cemented together and filled into the pores of soil skeleton based on the specific MH saturation. The drained triaxial compression tests with different MH saturation and effective confining pressures were conducted to analyze the mechanics, deformation characteristics and contact fabric of the pore-filling type of MHBS. The results show that the influence of MH saturations on the initial elastic modulus and deviator stress is relatively small. The volume shrinkage decreases with increasing MH saturations under the same effective confining pressure while the strength and the volume shrinkage increase with the effective confining pressure increasing under the same MH saturation. The shear dilatancy angle almost linearly decreases with the increase of effective confining pressure, and it linearly increases with MH saturations increasing. The grain contact direction deflects to the vertical direction with the increase of axial strain.

Key words：distinct element method (DEM); pore-filling type of methane hydrate-bearing sediment (MHBS); numerical technique; MH saturation; mechanical behavior; contact fabric

收稿日期：2015-09-07

基金项目：国家杰出青年科学基金(51025932);国家自然科学基金(51179128，51579178);土木工程防灾国家重点实验室基金(SLDRCE14-A-04)

中图分类号：TU43

文献标志码：A

第一作者： 贺洁(1987—)，女，博士生，主要研究方向为挡墙土压力理论分析及数值模拟，深海能源土的离散元数值模拟及宏微观本构理论.E-mail:12hejie@tongji.edu.cn