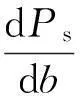文克勒地基板极限承载力的弹塑解

谈至明， 姚　尧， 郭晶晶

(同济大学 道路与交通工程教育部重点实验室，上海 200092)



文克勒地基板极限承载力的弹塑解

谈至明， 姚尧， 郭晶晶

(同济大学 道路与交通工程教育部重点实验室，上海 200092)

摘要：将圆形均布荷载作用下的文克勒地基板出现环状裂缝时的板划分为二个区域，环内屈服区仍采用刚塑性假设，而环外弹性区采用线弹性假设，进而推导得到了文克勒地基上板极限承载力的弹塑性解，其中，环状裂缝出现位置由板承载力最小化条件求出，从而弥补了现有刚塑性理论解中不能确定环状裂缝出现位置的缺陷，使理论解更完备且具有良好的拓展性.分析结果表明，梅依尔霍夫的地基板承载力的解偏大且在圆形均布荷载相对半径ρa=2.925时发散，在ρa=0.09～0.70范围时，梅氏解偏大6%～10%.最后，为简便使用给出了弹塑性解的板极限承载力系数φE回归式.

关键词：地基板； 极限承载力； 刚塑性； 弹塑性； 混凝土铺面； 环状裂缝位置

水泥混凝土地坪、堆场和路面等铺面结构的极限承载力是土木工程力学中典型问题之一，早在20世纪40年代，对此问题开展了不少试验和理论研究，发现水泥混凝土铺面结构在圆形荷载作用下，铺面结构的工作状态可分弹性、中央区屈服、环状裂缝出现和冲剪破坏四个阶段，并将环状裂缝出现时的荷载量作为水泥混凝土铺面极限承载力[1-2].对此的力学解析以梅依尔霍夫为代表，他将水泥混凝土铺面视为文克勒地基板，并用刚塑理论拟合板的变形，这种忽略板弹性变形的近似处理方式导致无法在理论上获得环状裂缝的位置，对此，梅依尔霍夫总结了大量试验结果,给出了环状裂缝位置经验值[1].梅氏的水泥混凝土极限承载力计算方法获得了广泛的应用，例如，在英国工业混凝土地坪设计方法中被采用[3-4].但是，从理论上来看梅氏方法是不够完善的，一旦当地基板结构或荷载圆半径超过梅氏当年的试验范围，直接应用梅氏公式的精度就难以保证了.另外，蒋大骅[2]指出梅氏板中荷载的板极限承载力公式仅是一个上限解，叶又等[5]应用弹塑性有限元研究了钢纤维混凝土路面板的极限承载力后指出，板环状破裂面与梅氏解不符，但未能总结其规律，因此，有必要对此问题开展更深入的研究.

1文克勒地基板极限承载力的刚塑解

随着作用于文克勒地基板的圆形均布荷载的荷载集度持续增大，荷载圆中心点的板底弯拉应力达到材料抗弯强度，板由弹性转入屈服状况，而后，从荷载圆中心为起点的径向裂缝开始萌生、扩展、伸长，直到距离板中心某一半径r=b处的最大负弯矩所产生的弯拉应力达到板的抗弯强度，板结构到达了极限状态：环形裂缝出现.根据刚塑性理论，板的极限状态如图1所示意，其中，w0为荷载中点的板挠度;a为圆形均布荷载半径;q为荷载集度.

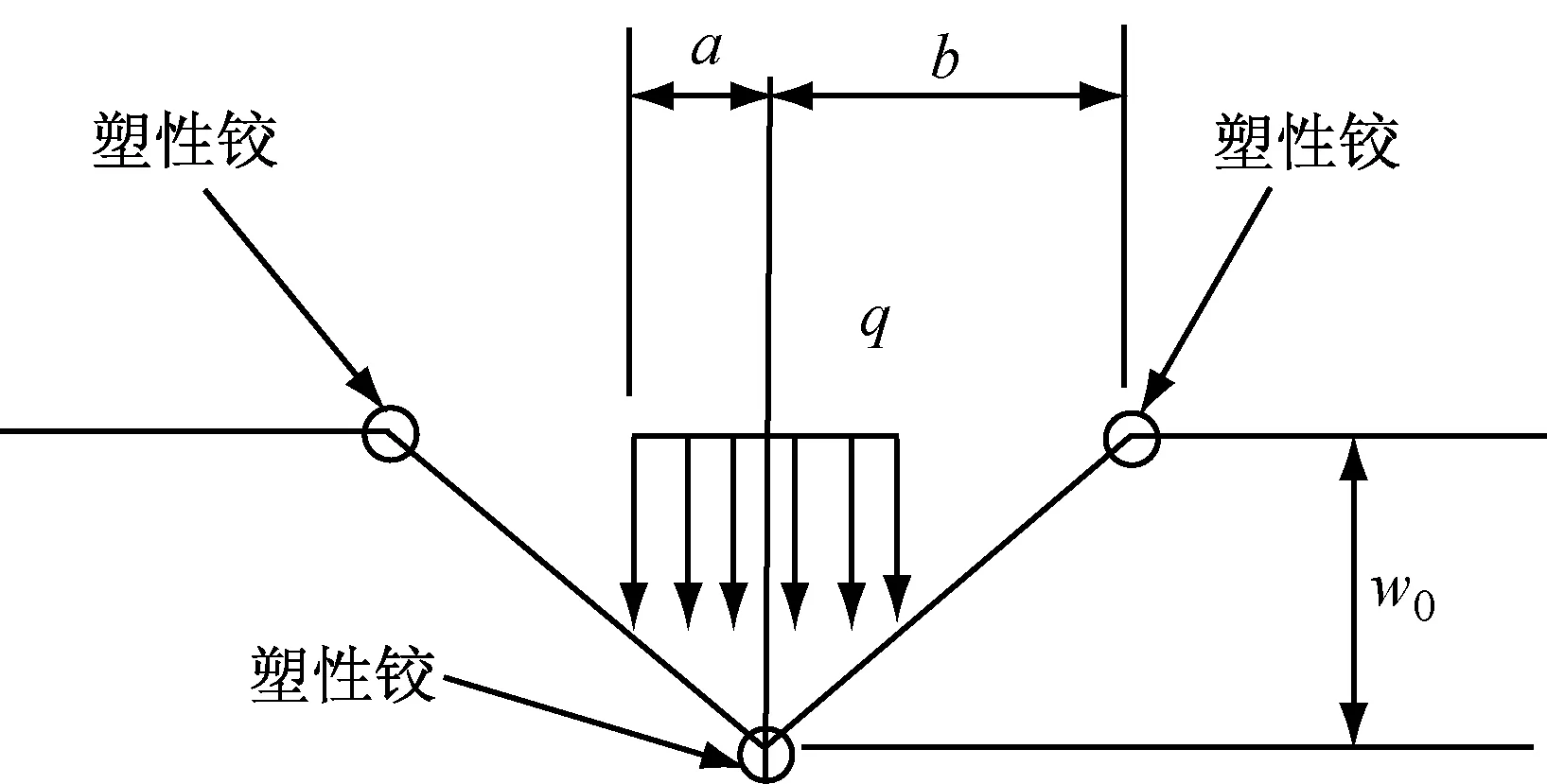
图1　板中受荷的极限状态

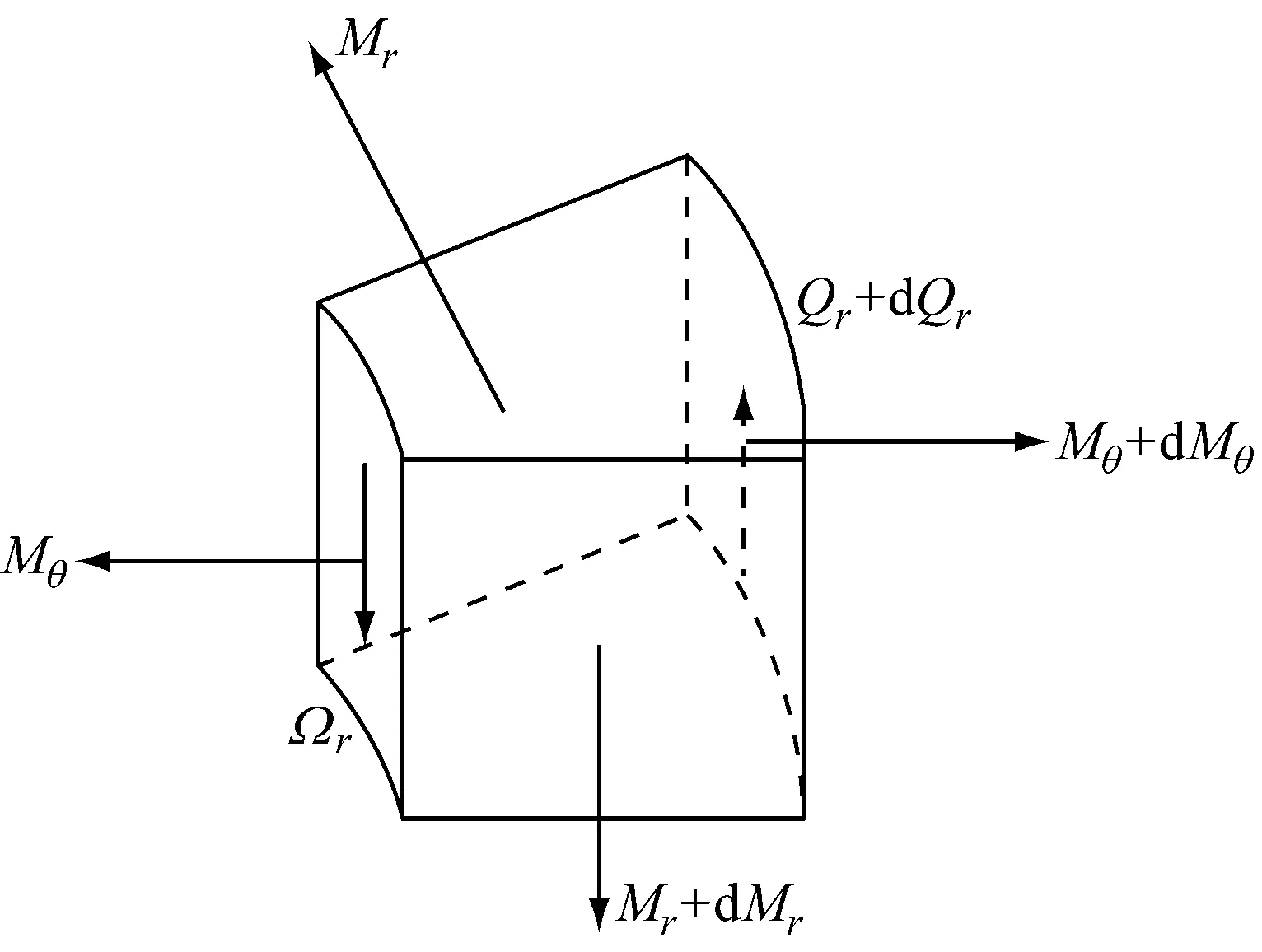
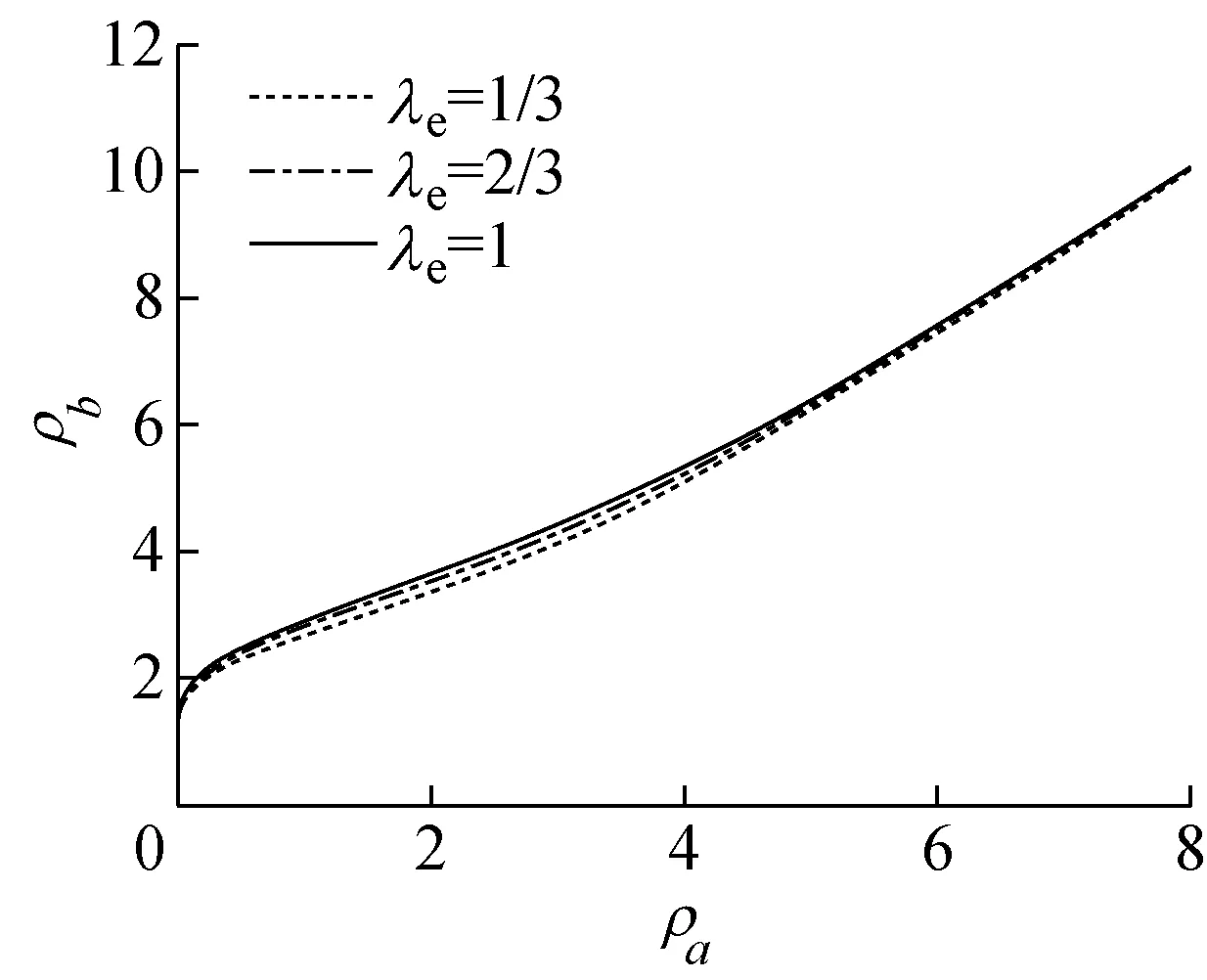
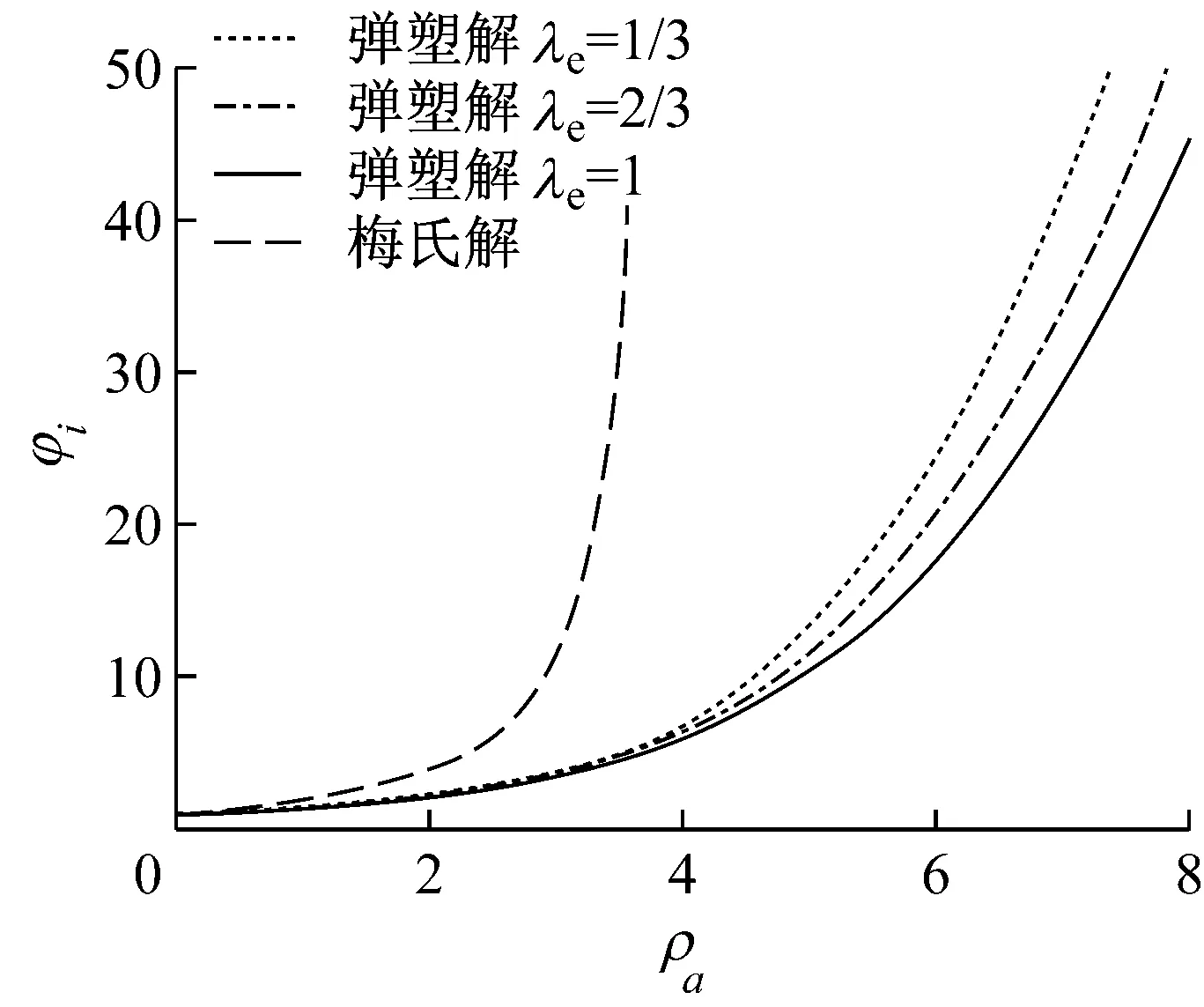
在r

(1)

由静力平衡条件，圆形均布荷载合力P为

(2)

式中：k为文克勒地基的反应模量.

取板一微分单元(图2)，其板平衡微分方程为

(3)

式中：Mr为径向弯矩；Qr为径向剪力；Mθ为切向弯矩，它在整个屈服区均达了屈服弯矩，即Mθ=Me.

图2　板微分单元

解式(3)得：

(4)

r=b时，剪力Q(b)=0，径向弯矩达到板限弯矩Mr(b)=-Ms，由此得到文克勒地基板极限承载力的刚塑性解为

(5)

式中：λe为板屈服弯矩与极限弯矩之比，即λe=Me/Ms.

由于Ps与b之间关系是单调，Ps随着b增大而减小，因此，无法求出Ps极值.梅依尔霍夫根据大量试验指出，荷载圆半径a与环形裂缝半径b之比a/b在0.050～0.750范围时，b=3.9l，其中，l为文克勒地基板的相对刚度半径,即

式中：E,ν分别为板弹性模量和泊松比；h为板厚度.

2文克勒地基板极限承载力的弹塑解

在环形裂缝之外的区域(r≥b)，地基板始终处于弹性状态，其力学问题即为文克勒地基带孔无限大薄板的边值问题，在r=b边界，有径向弯矩Mr(b)=-Ms，Qr(b)=0(可从式(3)推出)，由此得到以下带孔无限大文克勒地基板的边值问题：

(6)

本问题属齐次轴对称问题，板挠曲微分方程解可表示为[5]

(7)

由无穷收敛条件得到待定常数B3=B4=0，径向弯矩Mr和径向剪力Qr的表达式为

(8)

将ρ=ρb=b/l的二边界条件代入式(8)联立解得待定常数B1,B2为

(9)

环形裂缝内侧的板挠度可表示为

(10)

由静力平衡条件，得到圆形荷载合力P与板中心点及环形裂缝处挠度w0,wb的关系为

(11)

由此得到，文克勒地基板的极限承载力Ps的表达式为

(12)

式中：ξb为环裂处的挠度系数.

(13)

式中：ρa=a/l.

式(13)是非常系数微分方程，需应用数值解求得.计算结果表明，材料泊松比的影响甚小，可忽略.图3给出了不同屈服弯矩与极限弯矩比λe条件下ρa与ρb的关系曲线.从图3中可以看出，λe值对出现环状裂缝的相对位置ρb影响也很小；ρb值随着圆形均布荷载相对半径ρa的增大而增大，在ρa很小时，ρb稍小于2，当ρa>4以上，ρb与ρa的关系近似线性，两者之比ρb/ρa趋近1.25.

将对应极限承载力极小值的ρb代入式(7)即可得到环状裂缝处的板挠度系数ξb，进而利用式(11)求出文克勒地基板极限承载力Ps.

图3　板极限状态ρa与ρb的关系

3弹塑性解的讨论和比较

弹塑性解中，板出现环状裂缝时的地基板挠曲形状如图4示意.在刚塑解中，环状裂缝位置b和板挠度零点位置c合一，在弹性解中两者相距(c-b)为1.32l～1.16l；其次，环状裂缝处的板挠度系数ξb变化幅度较小，荷载圆相对半径ρa从0增至8，ξb从0.61增至0.95，见图5.

图4　地基板挠曲示意图

按梅依尔霍夫所言,a/b在0.05～0.75范围内,当b=3.9l时，ρa值的变化范围在0.20～2.93之间，而对应b=3.9l的弹塑性解的ρa值为2.40，即a/b=0.615，也就是说ρa值缩减至0.09～2.40之间；若将刚塑性解的环状裂缝位置b改为板挠度零点位置c，则ρa适用范围缩小至0.20～0.70之间.

为了比较弹塑性解和刚塑性梅氏解的差异，将板极限承载力Ps表示为

(14)

图5　ξb与ρa,(ρc-ρb)与ρa关系图

式中：φi可称为之板极限承载力系数，i=E为弹塑性解，i=M为梅氏解.

两种不同解的板极限承载力系数φ见图6.从图6可以看到，梅氏解是偏大，在ρa很小时，φM偏大5%，ρa=0.70时φM偏大10%；ρa=0.09～0.70范围内，梅氏解平均偏大8%；ρa超过1.5之后，偏差迅速上升，并在ρa=2.925时趋向无穷.

图6　极限承载力系数φ图

常见荷载的ρa值不大于0.7，载重卡车的轮载相对道路水泥混凝土路面而言，ρa值约在0.1～0.3之间；集装箱单箱角荷载相对水泥混凝土堆场铺面的ρa值不大于0.1，多列箱箱角荷载的ρa值在0.1～0.4之间；吊车、起重机支腿的ρa值一般小于0.6，因此，利用梅氏解估计混凝土铺面板极限承载力约偏大5%～10%，破裂环出现位置偏差更大些，两者之差超过1倍板相对刚度半径.

考虑到开尔文函数不常用，且计算环状裂缝位置b和该处弹性挠度wb不太简便，为此对φE与ρa之间关系进行回归.当ρa<8且误差不足1%时,回归式为

(15)

若ρa值在0.09～0.70范围内，即满足梅氏关于荷载圆半径与环状裂缝半径(板挠度零点半径)比的要求，板极限承载力Ps可直接对梅氏解除以1.08即可，其偏差不大于2%.

4结语

将圆形均布荷载下的文克勒地基上板出现环状裂缝时的板划分为二个区域，环状裂缝内侧的中心屈服区采用刚塑性假设，即为倒圆锥形；环外区域采用线弹性假设，即为开孔无限大文克勒地基薄板的边值问题，联立上述两个解，由板承载力最小化条件求得环状裂缝出现位置，从而得到了板极限承载力的弹塑性解.对于有限尺寸圆板，出现环状裂缝的圆板临界相对半径ρR约比出现环状裂缝的相对位置ρb大1～2；大于临界相对半径的有限尺寸圆板极限承载力变化很小,可忽略.此解弥补了现有基于刚塑性理论的极限承载力解存在不能确定环状裂缝出现位置的缺陷，使理论解更完备且具有良好的拓展性.

随后，分析了弹塑性解的特征规律，并与刚塑性解进行比较.分析比较结果表明，环状裂缝出现在地基反力锥形区内，其相对位置ρb的板挠度系数ξb在0.61～0.95范围内变化；梅依尔霍夫给出的环状裂缝位置(3.9l)仅是a/b=0.615的特例，其解偏大且在ρa=2.925时发散，在ρa=0.09～0.70范围时，梅氏解偏大6%～10%.最后，为简便使用给出了弹塑性解的板极限承载力系数φE回归式.

参考文献:

[1]Meyerhof G G. Load carrying capacity of concrete pavements[J]．Journal of the Soil Mechanics and Foundations Division， 1962, 88(2): 11.

[2]蒋大骅．关于混凝土地面的承载能力[J]．同济大学学报，1980(1): 17．

JIANG Dahua. On the bearing capacity of concrete ground[J]. Journal of Tongji University, 1980(1): 17．

[3]Geoffrey Griffiths，Nick Thom. Concrete pavement design guidance notes[M]. New York: Routledge Press, 2007.

[5]叶又,刘效尧,吴长春.钢纤维混凝土路面板极限承载力的有限元分析[J]．中国公路学报， 1997,10(2):11.

YE You, LIU Xiaoyao, WU Changchun. Analysia of load carrying capacity of steel fibre concrete pavement by FEM[J]. China Journal of Highway and Transport, 1997, 10(2):11.

Elastic-Plastic Solution to Ultimate Bearing Capacity of Plate on Winkler Foundation

TAN Zhiming, YAO Yao, GUO Jingjing

(Key Laboratory of Road and Traffic Engineering of the Ministry of Education, Tongji University, Shanghai 200092, China)

Abstract：The plate on Winkler foundation with circumferential crack was divided into two areas under circular uniformly distributed load. Rigid-plastic hypothesis was used inside the circumferential crack and linear-elastic hypothesis was used outside it. Then, the elastic-plastic solution to ultimate bearing capacity of plate on Winkler foundation was given. Besides, the position of annular crack was found on the condition of minimal ultimate bearing capacity, which could compensate for the defects that the location of the annular cracks could not be solved using the existing rigid-plastic theory. It is more complete and has good expansibility. The result shows that the Meyerhof’s solution to ultimate bearing capacity of plate is larger and divergent when the relatively radius of circular uniformly distributed load is 2.925. The Meyerhof’s solution is 6% to 10% larger when the relatively radius of circular uniformly distributed load is between 0.09 and 0.7. Finally, a more convenient regression formula of ultimate bearing capacity of plate coefficient was proposed.

Key words：foundation plate; ultimate bearing capacity; rigid-plastic; elastic-plastic; concrete pavement; position of annular crack

收稿日期：2015-06-02

基金项目：国家自然科学基金(51378394)

中图分类号：TU313

文献标志码：A

第一作者： 谈至明(1960—)，男，教授，博士生导师,工学博士，主要研究方向为路面工程.E-mail：13901779114@126.com