某乘用车制动盘冷却特性的研究

杜旭之, 杨志刚, 李启良, 赵兰萍

(1.同济大学 上海地面交通工具风洞中心,上海 201804； 2.同济大学 机械与能源工程学院,上海 201804)



某乘用车制动盘冷却特性的研究

杜旭之1, 杨志刚1, 李启良1, 赵兰萍2

(1.同济大学 上海地面交通工具风洞中心,上海 201804； 2.同济大学 机械与能源工程学院,上海 201804)

摘要：基于某SUV的整车环境，利用数值计算和热环境风洞(CWT)试验的方法，探索了重复制动工况下制动盘的温升和冷却过程，分析了制动盘冷却过程中的散热方式以及冷却特性.结果表明,计算流体力学(CFD)得到的温升和冷却特性曲线与试验结果的一致性较好；对流散热是影响制动盘冷却性能的主导因素；制动盘的温度随冷却时间呈指数关系下降，冷却系数随汽车来流速度呈幂律关系增长.

关键词：制动盘； 计算流体力学； 热环境风洞试验； 冷却系数

制动器的温度过高会导致整车的制动性能下降，同时给整个制动系统带来各种不良的影响，例如踏板行程增加、制动盘热衰退、磨损寿命降低、制动液沸腾以及盘面热应力裂纹等[1-2].因此为保证行车制动的安全性，尤其是在制动系统的设计前期，必须快速有效地对制动盘或制动鼓的温升和冷却性能进行有效的计算、分析和优化，这样才能保证汽车制动性能优异的前提下使汽车的研发周期和成本趋于最小化.目前研究制动盘热性能比较主流的思路是基于数值和试验相结合的方法，然而在整车环境下，制动盘热性能的试验成本较高、试验周期较长；另外整车CFD计算的几何处理、网格划分、计算时间及计算精度等因素给数值计算增加了额外的困难；因此前人的研究大多是基于单个制动盘进行的[3-19]，少量文献[8,20-21]对整车工况下制动盘的热性能进行了初步的数值和试验探索.

高温制动盘在冷却过程中主要以对流传热和热辐射的形式进行散热[7].文献[7]通过对单个制动盘的数值和试验研究，发现其在冷却过程中，有90%以上的热量以对流传热的形式带走，通过热辐射带走的热量则不到10%.对于制动盘冷却性能的研究，前人大多从冷却时间和对流换热系数等角度进行分析[3,8-11,20,22]，然而在近几年，少数学者开始提出用“冷却系数”的概念来研究和评估制动盘的冷却性能，例如文献[7]中作者通过对单个制动盘的冷却特性曲线进行回归分析和拟合，提出了冷却系数的概念，以此来衡量制动盘的冷却性能，同时得到了冷却系数随来流速度呈线性增长的关系；另外文献[12-13]中作者也提出了冷却系数的概念，但并未对其物理意义进行深入的研究.

单个制动盘热性能的研究并不能有效地再现整车环境下制动器周围复杂的热、流场结构，同时也无法充分考虑汽车发动机、底盘以及车身等结构对于研究结果的影响，因此本文基于某SUV真实车型，建立整车环境下制动盘的热流耦合CFD数值模型，同时进行相应的整车热环境风洞(CWT)试验，以此来探索重复制动工况下制动盘的温升和冷却过程，并基于传热学理论，从冷却系数的角度分析制动盘的冷却特性，旨在为制动盘热性能的数值计算、试验方法以及冷却特性的研究和评估提供参考.

1CFD数值计算

1.1整车计算模型

基于某SUV实际车型，建立包含发动机、底盘、车身等较为详细的整车几何模型，如图1所示.其中该车前后轮均配备盘式制动器如图2所示，盘内的通风道由36个直方肋板构造而成.

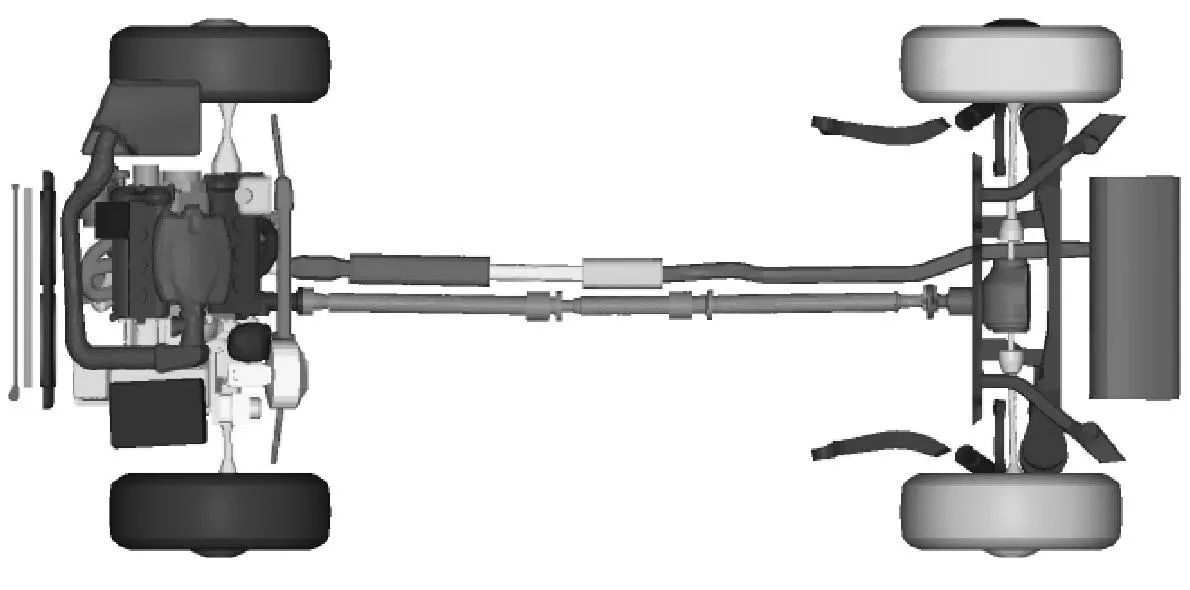
图1　整车的发动机、底盘、车身模型

图2　制动盘的三维模型及风道剖面图

1.2网格划分

考虑到整车模型的复杂性，几何表面采用三角形网格进行划分，空气和固体区域则分别生成相应的四面体网格.车身面网格大小为16 mm，发动机网格大小为3 mm，制动盘面网格大小为1 mm，其余底盘部件的网格大小为10 mm.为了更准确地预测车身表面空气的流动情况，在汽车外表面生成了五层边界层网格[23]，第一层厚度为1 mm，增长率为1.1.如图3所示，整车放置在一个长L、宽W、高H分别为10L，5W和4H的计算域中，最后得到体网格的总数为2 700万.

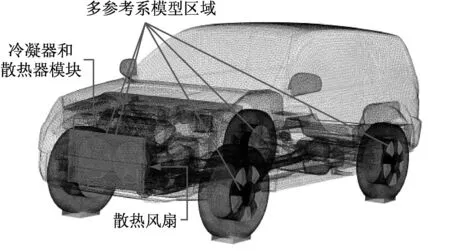
图3　整车面网格与计算域

1.3参数设置

(1) 材料物性参数：计算域内空气设为理想不可压缩气体，导热系数随温度变化[24].制动盘的材料为铸铁，其他底盘部件的材料主要为钢，发动机的材料主要为铝，材料具体的物性参数可参考文献[24]，CFD计算时其环境温度设为10 ℃.

(2) 多孔介质区域：发动机前方的冷凝器和散热器(图3)定义为多孔介质区域，其数值模型源自Darcy定律，即

(1)

式中：Si是i向动量源项；α为多孔介质的渗透性因子；μ为黏性系数；c3为惯性阻力因子；ρ为流体密度；v为平均速度;vi为平均速度分量.具体数值可参考文献[25].

(3) 运动区域：为了真实地模拟车轮、制动盘以及风扇的旋转效应[26]，制动盘的通风道、车轮轮辐、以及汽车发动机舱内两个散热风扇所在的区域均设为多参考系模型(MRF)区域[27](图3)，地面移动的模拟则通过Moving Wall的功能实现[26-27].

(4) 边界条件：为确保数值计算和试验具有对比性，考虑试验条件限制的同时参考国标GB 21670—2008设定车速从72～36 km·h-1的重复制动工况，如图4所示，其制动周期为20 s.制动过程中，产热功率的计算和修正具体参考文献[21,28].如图3所示，计算域边界条件采用速度入口，入口速度利用自定义函数(UDF)参考图4所示的工况进行编辑和定义，出口采用压力出口，壁面采用对称边界条件，制动盘的产热功率参考图4所示的工况利用UDF进行定义，制动盘与空气之间的边界面采用对流边界条件[24].

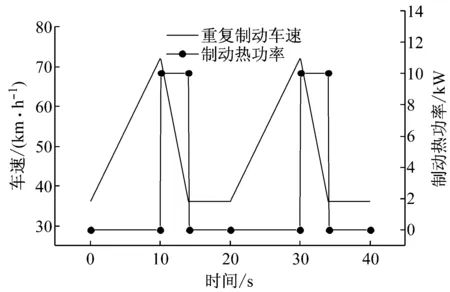
图4　重复制动工况和制动产热功率

(5) 湍流模型[29-30]和计算：第一步，采用Realizablek-ε两方程湍流模型计算得到流场的定常解，其中近壁面区采用标准壁面函数，各计算残差设为10-4；然后，在第一步的基础上，通过能量方程和DO热辐射模型进行温度场的非定常计算，其中，时间步长设定为1 s，单个时间步长内迭代30次，能量残差设为10-7.计算软件为Fluent12.0，计算平台为上海地面交通工具数值风洞中心刀片服务器.

2热环境风洞试验

为了排除道路试验侧风等外在因素对试验的影响，本文制动盘热性能试验在上海地面交通工具风洞中心(SAWTC)的热环境风洞(CWT)中进行.CWT内配备了齐全的温湿度控制系统、道路模拟转毂系统以及风速闭环控制系统，其主要参数如表1所示.

表1　CWT的主要参数

其他试验设备器材主要包括滑环(Michigan Scientific Corporation)、K型热电偶、踏板力传感器、BusDAQ数据采集仪、计算机等，实验整体布局如图5所示.实验原理如下：将K型热电偶穿过制动盘螺栓孔并嵌入预先钻好的小孔中进行固定，以此来测量制动盘摩擦区域中心的温度，如图5所示，热电偶的测温触头位于摩擦区域中心.滑环通过螺栓安装在轮毂外侧并保持与车轮同轴，车辆运行中，K型热电偶的微电压信号通过滑环中的信号放大器并经由电刷和信号线传入车内的数据采集仪中，同时车轮的转速信号也经由滑环内部的轮速传感器传至数据采集仪中，因此制动盘的温度信号和车轮的转速信号均可通过滑环获得.此外，驾驶员根据从踏板力传感器获取的压力信号基本能够保持汽车重复制动过程中制动减速度的相对统一和稳定.试验过程中，信号具体的采集流程如图6所示.

试验期间，CWT的环境温度设为(10±0.5)℃，相对湿度为(55±0.5)%，各试验参数基本与CFD计算保持一致.

图5　重复制动CWT试验布置图

图6　CWT试验信号采集流程图

3结果与分析

3.1数值计算与试验结果的对比

图7所示为CFD计算和CWT试验的温升曲线.从图7可知，制动盘大约经历800～1 000 s的重复制动后，温度基本趋于饱和.通过比较，可以看出CWT试验制动盘的温升速率略大于CFD的计算结果，这是由于相比于CWT试验，CFD的几何模型忽略了制动盘周围某些精细复杂的几何部件，促使盘面周围空气流通的空间有所增加，气流的通过性有所增强，因此其对流散热性能优于实车的CWT试验，最后导致CFD计算得到的制动盘测点的温升速率及饱和峰值温度都略小于CWT试验.但从最后制动盘的饱和峰值温度来看(表2)，CFD计算与试验结果的一致性较好.

图7　温升阶段制动盘测点温度随时间的变化

Fig.7Temperature of measuring point versus time during heating process

表2　制动盘测点的峰值温度

图8所示为CFD计算和CWT试验的冷却曲线，其中冷却车速(汽车来流速度)为60 km·h-1，设定冷却的起始温度为500 ℃，环境温度为10 ℃.

由图8可知，在前400 s，CFD计算与CWT试验结果的一致性较好，两者曲线的斜率走向较为逼近.但是随着时间的推移，CFD计算得到的制动盘的冷却速率开始逐渐高于试验结果，其误差与CFD建模时几何模型的简化以及制动盘对流散热的权重有关，其原因将在下文3.2中具体分析.从图8制动盘的整个冷却过程来看，CFD计算与试验结果的最大误差不超过15 ℃，两者曲线的整体一致性较好，其误差基本在工程问题的接受范围之内.

Fig.8Temperature of measuring point versus time during cooling process

综合上述制动盘温升和冷却阶段CFD计算与CWT试验的比较，充分说明了利用数值计算的方法来研究制动盘在整车环境下的热性能，其计算结果的精度基本是可以接受的.当然CFD计算的误差还受到材料物性等参数的影响，同时CWT试验的结果也受到测量误差和汽车驾驶误差等因素的影响.

3.2制动盘冷却特性的分析

图9所示为60 km·h-1来流速度下，CFD计算得到的制动盘的辐射和对流散热量随时间的变化.由图9可见，在整个冷却过程中，制动盘90%以上的热量靠对流传热的方式带走，而通过盘面热辐射带走的热量则不到10%，并且随着时间的推移，辐射散热的比重逐渐减小，对流散热的比重逐渐增加，此结果与文献[7]中单个制动盘的计算结果较为一致.由于CFD几何模型的简化导致制动盘的对流散热性能略优于真实车型，促使数值计算时制动盘的冷却速率大于CWT的试验结果(图8)，并且随着对流散热比重的逐渐增加(图9)，计算与试验结果的误差也将随之增大(图8).

为评估和量化制动盘的冷却特性，首先从传热理论的角度提出了同时考虑对流散热和辐射散热影响的制动盘冷却系数，随后对冷却系数与汽车来流速度的关系进行研究和分析.

方程(2)，(3)分别为制动盘冷却过程中的对流散热量和辐射散热量[24].

图9　对流和辐射散热量随时间的变化

Fig.9Amount of the convective heat dissipation and radiative heat loss versus time

(2)

式(2),(3)中:qconv为对流换热量；hconv为制动盘对流换热系数；Ab为制动盘的表面积；T为冷却过程中经历时间t后制动盘的峰值温度；T∞为环境温度；qrad为辐射换热量；ε为辐射系数；σ为斯蒂芬-波尔兹曼常数.

由文献[13,31]可知，制动盘的毕渥数Bi(Biot Number)一般小于0.1，即

(4)

式中:h为对流换热系数；L为特征长度；k为导热系数.

因此制动盘冷却过程的能量守恒可用集总热容法(Lumped Capacitance Method)的形式来表达[24]：

(5)

式中:ρb为制动盘密度；cb为制动盘的比热容；Vb为制动盘的体积；t为冷却时间.

由方程(2),(3)得

(6)

式中:he为等效换热系数.

设t=0时，T=Ti(冷却初始温度)，对式(5)积分得

(7)

由式(7)定义制动盘的冷却系数为

(8)

则式(7)可整理成

(9)

式中：β为制动盘的冷却系数，s-1，其值越大，表示制动盘冷却的速度越快.

图10为CFD计算得到的不同来流速度条件下制动盘的峰值温度随时间的变化，显然随着来流速度的增大，制动盘的冷却速率也随之增大，但其增大的幅度呈逐渐减小的趋势.利用式(8)中冷却系数的概念对图10中制动盘的冷却曲线进行回归分析和最小二乘法拟合，得到来流速度与冷却系数的关系如图11所示，其中

(10)

式中：β为整车环境下制动盘的冷却系数，s-1；u为来流速度，km·h-1；

图10　不同来流速度条件下制动盘的峰值温度随时间的变化

Fig.10Brake disc peak temperature versus time at various oncoming velocities

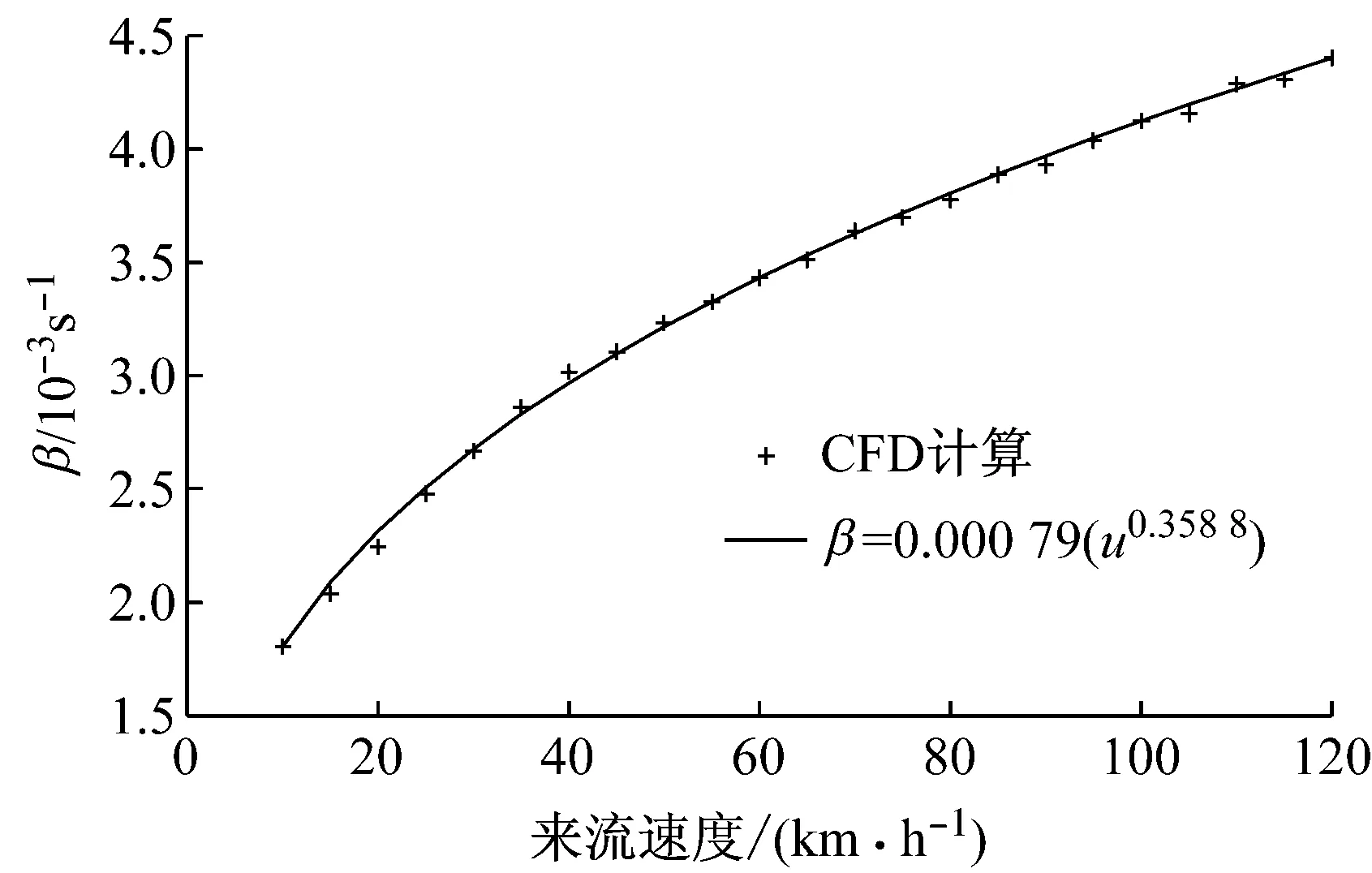
图11　来流速度与制动盘冷却系数的关系

Fig.11Correlation between cooling coefficient and oncoming velocity

从图11可知，制动盘的冷却系数随着来流速度的增加而增大，但其增幅逐渐减小，其趋势恰好解释了图10中制动盘冷却曲线斜率的变化，即随着来流速度的增加，制动盘的冷却速率逐渐增大，冷却性能逐渐增强，但是其增强的幅度逐渐减小；从曲线形态上表现出随着来流速度的增加，冷却曲线之间的距离将逐渐减小，因此相邻曲线在同一时刻的温度值也将逐渐的逼近，这从物理意义上说明，当来流速度超过某个临界区域时，制动盘冷却性能的提高将受到较大的限制，而这个临界区域的来源则可以通过研究冷却系数与来流速度的关系(图11)进行获取.这在汽车前期开发中对制动盘冷却性能的定义和优化具有积极的意义.

然而文献[7]通过对单个制动盘进行研究后发现，β与u的关系为

(11)

即单个制动盘研究中β与u呈线性关系增长，这显然无法准确地解释整车环境下，制动盘的冷却特性随时间的变化(图10)，因此对于单制动盘冷却特性的研究，其研究结论无法适用于整车环境下制动盘冷却特性的物理表达.

4结论

(1) 基于整车环境，通过CFD建立制动盘重复制动工况的热流耦合计算模型，其计算结果与热环境风洞试验结果的一致性较好，计算误差在5～15 ℃的范围内.

(2) 制动盘在冷却过程中，辐射散热所占的比例不到10%，可见对流散热将是未来制动盘散热优化的关键所在.

(3) 制动盘在冷却过程中，峰值温度随时间呈指数关系下降，冷却系数β随汽车来流速度呈幂律关系增长，其增长特性表明，当来流速度超过某个临界区域时，制动盘冷却性能的提高将受到较大的限制，因此冷却系数可用来评估制动盘的冷却性能以及指导制动盘来流通风的优化设计.

参考文献:

[1]余志生. 汽车理论[M]. 5版. 北京：机械工业出版社，2009.

YU Zhisheng. Automotive theory[M]. 5th ed. Beijing: China Machine Press, 2009.

[2]Lee K. Numerical prediction of brake fluid temperature rise during braking and heat soaking[J]. SAE Transactions, 1999, 108(6): 897.

[3]Jerhamre A, Bergström C. Numerical study of brake disc cooling accounting for both aerodynamic drag force and cooling efficiency[J]. SAE Transactions, 2001, 110(6): 1156.

[4]Hertel J E, Suster J R, Hawley J R,etal. Finite difference heat transfer model of a steel-clad aluminum brake rotor[C]∥SAE. Orlando: 23rd Annual Brake Colloquium & Exhibition, 2005: 2005-01-3943.

[5]蒋京, 夏群生, 余志生. 盘式制动器重复制动温度计算[J]. 汽车工程, 1996, 18(3): 168.

JIANG Jing, XIA Qunsheng, YU Zhisheng. Calculation of disc brake temperature in repeated braking[J]. Automotive Engineering, 1996, 18(3): 168.

[6]陈友飞, 李亮, 杨财, 等. 制动器热分析有限差分仿真模型的研究[J]. 汽车工程, 2012, 34(3): 236.

CHEN Youfei, LI Liang, YANG Cai,etal. A study on the finite difference simulation model for brake thermal analysis[J]. Automotive Engineering, 2012, 34(3): 236.

[7]Yigit S, Penther P, Wuchatsch J,etal. A monolithic approach to simulate the cooling behavior of disk brakes[J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2013, 6(3): 1430.

[8]Thomas S. Cooling analysis of a passenger car disk brake[C]∥SAE. Detroit: SAE International, 2009: 2009-01-3049.

[9]CHENG Qian. Aerodynamic shape optimization using CFD parametric model with brake cooling application[C]∥SAE. Detroit: SAE International, 2002: 2002-01-0599.

[10]Nutwell B, Ramsay T. Modeling the cooling characteristics of a disk brake on an inertia dynamometer, using combined fluid flow and thermal simulation[C]∥SAE. Detroit: SAE International, 2009: 2009-01-0861.

[11]Jeong B U, Kim H, Kim W,etal. Optimization of cooling air duct and dust cover shape for brake disc best cooling performance[C]∥SAE. Detroit: SAE International, 2014: 2014-01-2519.

[12]Johnston M, Leonard E, Monsere P,etal. Vehicle brake performance assessment using subsystem testing and modeling[C]∥SAE. Detroit: SAE International, 2005: 2005-01-0791.

[13]Barigozzi G, Perdichizzi A, Donati M. Combined experimental and CFD investigation of brake discs aero-thermal performances[J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2009, 1(1): 1194.

[14]Nisonger R L, Yen C, Antanaitis D. High temperature brake cooling-characterization for brake system modeling in race track and high energy driving conditions[J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2011, 4(1): 384.

[15]Choi B K, Park J H, Kim M R,etal. Development of the virtual test technology for evaluating thermal performance of disc brake[J]. Transactions of the Korean Society of Automotive Engineers, 2009, 17(4): 40.

[16]Kim M R, Ahn B J, Lee J M,etal. Numerical investigation of thermal behavior in brake assembly during the ALPINE braking mode[C]∥SAE. Detroit: SAE International, 2007: 2007-01-1021.

[17]Hwang P, Wu X, Jeon Y B. Repeated brake temperature analysis of ventilated brake disc on the downhill road[C]∥SAE. San Antonio: 26th Annual Brake Colloquium & Exhibition, 2008: 2008-01-2571.

[18]Liang L, Jian S, Xuele Q. Study on vehicle braking transient thermal field based on fast finite element method simulation[C]∥SAE. Orlando: 23rd Annual Brake Colloquium & Exhibition, 2005: 2005-01-3945.

[19]Choi B. Thermal performance of disc brake and CFD analysis[J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2014, 7(4): 1304.

[20]Mukutmoni D, Jelic S, Han J,etal. Role of accurate numerical simulation of brake cool down in brake design process[J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2012, 5(4): 1199.

[21]Travaglia C A P, Araujo J, Bochi M,etal. Analysis of drum brake system with computational methods[C]∥SAE. Rio Grande do Sul: 11° Colloquium Internacional SAE BRASIL de Freios & Mostra de Engenharia, 2013: 2013-36-0022.

[22]Schuetz T. Cooling analysis of a passenger car disk brake[C]∥SAE. Detroit: SAE International, 2009: 2009-01-3049.

[23]王福军．计算流体动力学分析：CFD软件原理与应用[M]．北京：清华大学出版社，2004．

WANG Fujun. Computational fluid dynamics analysis: theory and application of CFD software[M]．Beijing：Tsinghua University Press, 2004．

[24]Bergman T L, Lavine A S, Incropera F P,etal. Fundamentals of heat and mass transfer[M]. 7th ed. Jefferson: John Wiley & Sons, Inc, 2011.

[25]杨志刚, 苗露, 赵兰萍, 等. 轮毂电机驱动电动车流场特性数值计算研究[J]. 同济大学学报: 自然科学版, 2013, 41(12): 1872.

YANG Zhigang, MIAO Lu, ZHAO Lanping,etal. A study on flow field of four-in-wheel-motor driven vehicle[J]. Journal of Tongji University: Natural Science, 2013(12): 1872.

[26]Aus der Wiesche S. Heat transfer from a rotating disk in a parallel air crossflow[J]. International Journal of Thermal Sciences, 2007, 46(8): 745.

[27]Yang Z G, Bozeman J, Shen F Z. CFD for flow rate and air re-circulation at vehicle idle conditions[C]∥SAE. Detroit: SAE International, 2004: 2004-01-0053.

[28]周凡华, 吴光强, 沈浩, 等. 盘式制动器15次循环制动温度计算[J]. 汽车工程, 2001, 23(6): 411.

ZHOU Fanhua, WU Guangqiang, SHEN Hao,etal. Calculation of disc brake temperature in 15-cycle braking[J]. Automotive Engineering, 2001, 23(6): 411.

[29]Versteeg H K, Malalasekera W. An introduction to computational fluid dynamics: the finite volume method[M]. 2nd ed. Glasgow: Bell & Bain Limited, 2007.

[30]陶文铨．数值传热学[M]. 2版．西安：西安交通大学出版社，2001．

TAO Wenquan．Numerical heat transfer[M]. 2nd ed．Xi’an：Xi’an Jiaotong University Press, 2001．

[31]McPhee A D, Johnson D A. Experimental heat transfer and flow analysis of a vented brake rotor[J]. International Journal of Thermal Sciences, 2008, 47(4): 458.

Brake Disc Cooling Characteristics of a Passenger Car

DU Xuzhi1, YANG Zhigang1, LI Qiliang1, ZHAO Lanping2

(1. Shanghai Automotive Wind Tunnel Center, Tongji University, Shanghai 201804, China; 2. School of Mechanical Engineering, Tongji University, Shanghai 201804, China)

Abstract：A computational fluid dynamics (CFD) simulation was performed on a brake disc of an SUV during the repetitive braking and cooling process. The temperature rising and drop procedure were numerically investigated compared with the climatic wind tunnel (CWT) test, and the brake cooling characteristics was specifically analyzed based on the heat transfer theory. The results show that the CFD simulation and the experiments are in good agreement. The convection heat transfer acts as a key factor for the cooling performance of the brake. The temperature drop for brake disc exhibits an exponential function of the cooling time, while the cooling coefficient shows a power law increase with the oncoming velocity of the vehicle.

Key words：brake disc; computational fluid dynamics (CFD); climatic wind tunnel (CWT) test; cooling coefficient

收稿日期：2015-06-26

基金项目：国家“九七三”重点基础研究发展计划(2011CB711203)

通讯作者：杨志刚(1961—),男,教授,博士生导师,工学博士,主要研究方向为汽车空气动力学,热流研究及其控制.

中图分类号：U46

文献标志码：A

第一作者： 杜旭之(1989—),男,博士生,主要研究方向为汽车热环境及其控制.E-mail:2013xuzhi_du@tongji.edu.cn

E-mail:zhigang.yang@sawtc.com