基于二维模型的电梯井道空气流动分析

刘志仁+杨韡

摘要： 为研究电梯井道尺寸和电梯运行速度等对井道空气流动的影响，建立二维电梯井道模型，利用FLUENT对井道空气流动进行数值模拟.通过量纲分析和试验设计，针对不同阻塞比和雷诺数，选取60个样本点进行数值模拟，并建立流场参数的响应面.基于响应面的分析可知：轿厢阻力因数和井道空气最大流速比（最大流速与电梯运行速度之比）主要与阻塞比有关，并随阻塞比增大而变大；阻塞比和雷诺数都对轿厢表面的湍流强度和无量纲流场平均涡量都有影响.

关键词： 电梯井道； 空气流动； 响应面； 量纲分析； 试验设计； 计算流体力学

中图分类号： TU857文献标志码： B

Abstract： To study the effect of elevator shaft size and elevator speed on air flow in shaft， a 2D elevator shaft model is built and the air flow in shaft is simulated by FLUENT. By dimensional analysis and design of experiment， sixty sample points with different blockage ratio and Reynolds number are selected to perform numerical simulation and the response surfaces of the parameters of air flow field are built. The analysis on response surfaces show that， both the drag factor of cage and the maximum velocity ratio （ratio of maximum velocity and elevator speed） are mainly influenced by the blockage ratio， and they increase with the increase of the blockage ratio； both the drag ratio and the Reynolds number have some effect on the urbulence intensity on cage surface and nondimensional average vorticity.

Key words： elevator shaft； air flow； response surface； dimensional analysis； design of test； computational fluid dynamics

收稿日期： 2014[KG*9〗08[KG*9〗05修回日期： 2014[KG*9〗09[KG*9〗17

作者简介： 刘志仁（1986—），男，湖南耒阳人，硕士研究生，研究方向为空气动力学、气动声学以及振动与噪声分析，（Email）hnanlzr@163.com0引言

电梯轿厢在井道里运行时，其活塞效应会对前方的空气进行挤压，使空气通过轿厢与井道间的狭隘空隙绕过轿厢向后流动.空气在流过狭隘空隙时，运动速度会提高，流动的形态也会变得更加混乱.这些被加速的空气反过来也对轿厢产生影响，从而增加电梯运行过程中的阻力、噪声和振动.[14]

一般认为，轿厢表面的湍流会对轿厢形成波动载荷，强迫其振动，进而使其结构产生振动声辐射，对轿厢内产生较大噪声影响.[5]另外，根据涡声理论，低马赫数条件下的等熵绝热流体产生流体动力场和辐射声场的基本且唯一的源是涡.[67]流场中涡量的强度在一定程度上代表气动噪声的水平.

目前，国内外针对高速电梯的气动研究主要包括整流罩优化、泄压孔计算、噪声预测等.李晓冬等[8]采用CFD数值计算模拟方法比较6种不同轿厢整流罩的性能.鲁国雄[9]基于二维模型分析泄压孔对井道空气流动的影响.PIERUCCI等[10]利用FLUENT仿真轿厢过层门地坎时受到的冲击力，并与试验值进行对比.

本文基于响应面方法，分析井道面积、电梯运行速度对轿厢气动阻力、井道空气流速、轿厢表面湍流强度、井道空气涡量强度等的影响，为高速电梯井道面积制定、井道泄压孔开设标准提供依据.

1二维模型的建立和无量纲化

为分析电梯运行时井道内空气流动的主要特征，将电梯轿厢的外形简化为一个长方体，并忽略井道内的导轨等设施，得到井道内布置的俯视图见图1.取图中的二维剖面位置作为井道空气流动分析对象，得到井道二维模型.

当电梯在井道中间段全速运行时，若井道足够高，则可以忽略井道高度对电梯轿厢附近流场的影响.另外，对于同一型号的电梯，可以认为轿厢高度保持不变.因此，对于二维电梯井道模型，井道空气流动由电梯运行速度vc，轿厢宽度wc，井道宽度ws，空气密度ρ和空气黏度μ决定.选取井道流场分析的目标变量为电梯匀速运行时井道中的空气最大流速vm，轿厢阻力d，轿厢表面平均湍流动能kc和流场平均涡量ζ.

在进行试验设计前，通过量纲分析，可以减少需要分析的变量个数，简化分析量.[11]针对以上变量进行量纲分析，可以得到如下无量纲量.

1）阻塞比ra=wcws；

2）雷诺数Re=ρvcwcμ；

3）最大流速比rv=vmvc；

4）轿厢阻力因数Cd=d12ρv2cwcm

5）轿厢表面平均湍流强度I=23kcvc

6）无量纲流场平均涡量ζ′=wcζvc

ra和Re是试验需要研究的自变量；rv，Cd，I和ζ′是因变量.

2数值计算

2.1几何模型

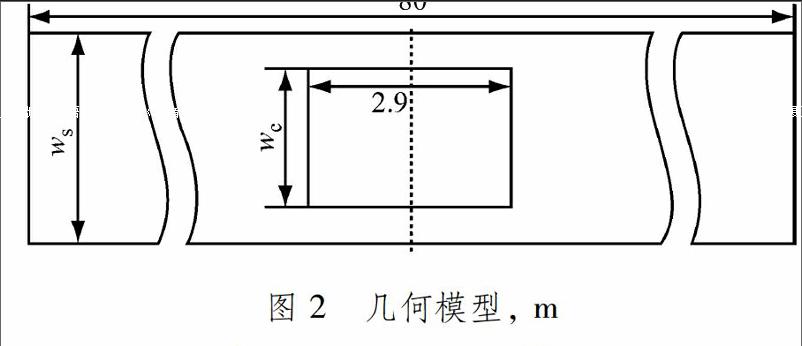
计算采用的二维几何模型见图2.井道长度为80 m，轿厢处于井道中间位置，轿厢高度为2.9 m，.电梯轿厢宽度wc和井道宽度ws由计算时指定的阻塞比确定.

2.2网格

二维井道模型几何形状简单，可以很方便地生成全结构网格.但鉴于结构网格不方便控制远场网格密度，因此采用结构四边形和非结构四边形的混合网格：轿厢和井道壁面采用结构网格生成边界层；轿厢上游1个轿厢高度和下游5个轿厢高度的区域内，采用非结构网格进行加密；井道内其余区域采用结构网格.共生成网格数量约25万个，具体网格拓扑见图3和4.

2.3求解参数

电梯在井道中间段匀速运行时，井道流场基本稳定，因此可以采用定常计算以节省计算成本.同时，电梯运行速度较低，井道内的空气流速远小于当地声速，可以认为空气不可压缩.

为简化计算，设电梯轿厢静止不动，而井道空气和井道壁面相对于轿厢运动，速度大小与轿厢运行速度相同、运行方向相反.轿厢壁面为静止壁面边界条件，井道壁面为移动壁面边界条件，井道的一端为速度入口边界条件，另一端为压力出口边界条件.

采用FLUENT进行流场计算，选取湍流模型为kω SST模型，采用2阶离散格式以提高计算精度.

2.4计算结果和分析

计算得到的流场压力云图和速度云图分别见图5和6.由此可知：电梯运行时在轿厢顶部形成正压区，而在轿厢的后部尾迹区存在负压；轿厢的两侧空气流动存在明显分离，同时流过的空气被加速.

3响应面模型

3.1试验设计

为提高试验效率，在保证试验效果的同时减少试验次数，需要进行试验设计.采用优化空间填充设计方法进行试验设计.试验变量为：阻塞比ra的取值范围为[0.4， 0.7]，雷诺数Re的取值范围为[1.36×105， 3.4×106].在变量取值范围内选取60个样本点分别进行数值仿真.这些样本点在设计空间上的分布见图7.统计并拟合所有样本点的计算结果，可以分别得到无量纲参数最大流速比rv，轿厢阻力因数Cd，轿厢表面平均湍流强度I和流场平均涡量ζ′的响应，从而建立各自参数对应的响应面模型.

3.2响应面分析

响应面的拟合优度见表1.响应面的决定因数越接近1，平均相对误差越小，则响应面的质量越好.由表1可知，4个响应面的决定因数都非常接近1.同时，各响应面的平均相对误差也在5%以内，因此可以认为响应面的拟合质量符合要求.

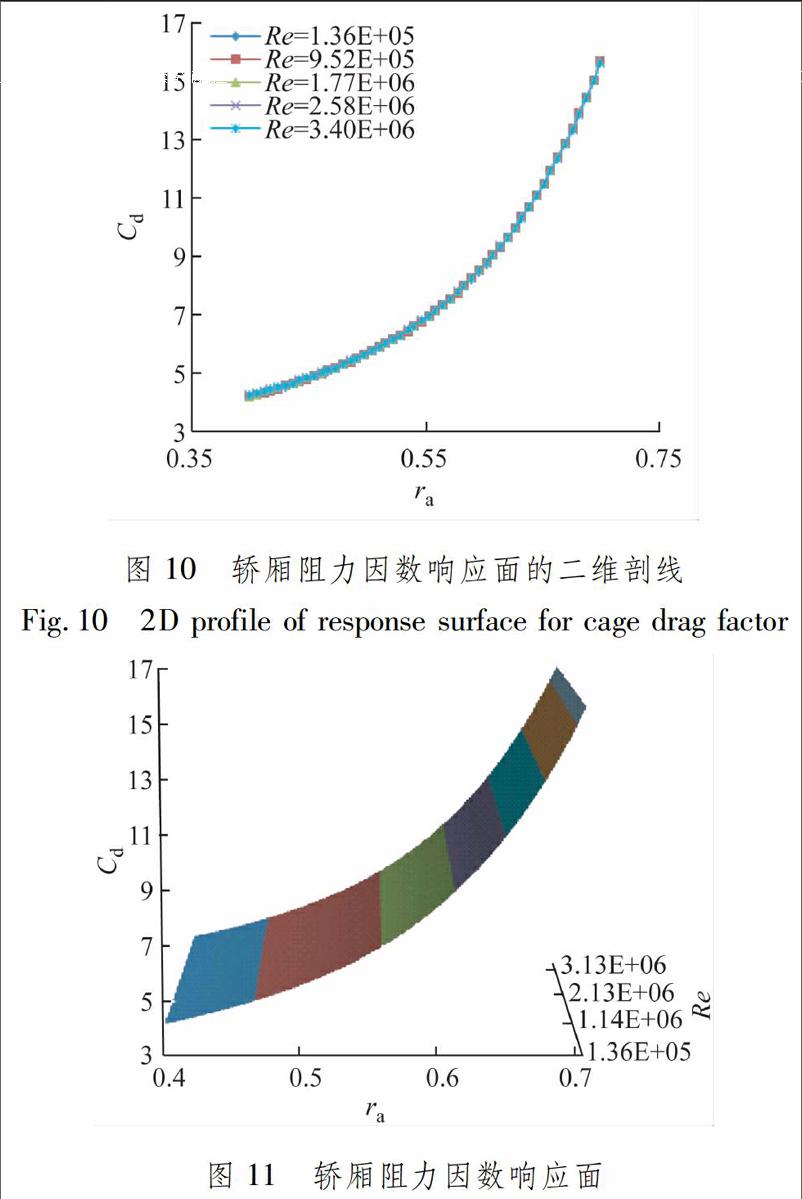
轿厢阻力因数Cd的二维剖线和三维响应面分别见图10和11.与rv类似，Cd只与ra有关，并随ra增大而迅速变大.对于某一特定井道，ra不变，轿厢阻力与vc的二次方成正比.

4结论

通过建立二维井道模型，利用CFD对井道流场的进行数值模拟，并建立流场参数的2阶多项式响应面模型，可以得到以下结论.

1）轿厢阻力因数Cd和井道空气最大流速比rv主要与井道的阻塞比ra有关.当ra增大时，Cd迅速变大，rv同样也变大，但变化速度较缓.

2）当井道和轿厢尺寸固定不变时，轿厢阻力d与电梯运行速度vc的二次方成正比，井道空气最大流速vv与vc成正比.

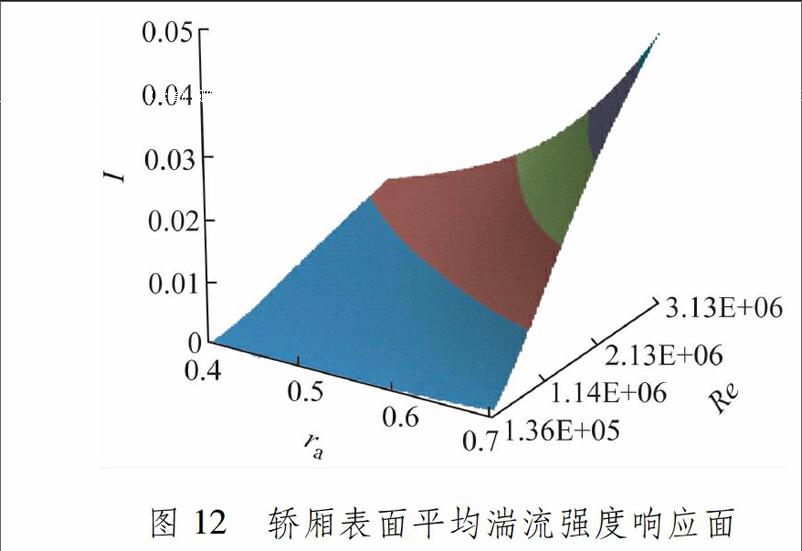
3）当流动的Re较低时轿厢表面的平均湍流强度I较小.随着Re的增加，I变大，并且ra越大时，I随Re增加的速率越大.

4）无量纲流场平均涡量ζ′随Re增加而减少，随ra增加而变大.

参考文献：

[1]BAI H， SHEN G， SO A. Experimentalbased study of the aerodynamics of superhighspeed elevators[J]. Building Services Eng Res & Technol， 2005， 26（2）： 129143.

[2]YANG H W， SO A T P. A 2dimensional aerodynamic model for superhighspeed elevators[J]. Int J Elevator Eng， 1998（2）： 1932.

[3]SCHETZ J A. Aerodynamics of highspeed trains[J]. A Rev Fluid Mech， 2001， 33（1）： 371414.

[4]王从陆， 吴超. 基于移动参考框架的矿内运输工具活塞风数值模拟[J]. 煤炭学报， 2007， 32（8）： 838841.

WANG Conglu， WU Chao. Numerical simulation of piston wind due to mine conveyance based on motion reference frame[J]. J China Coal Soc， 2007， 32（8）： 838841.

[5]张曙光. 350 km/h 高速列车噪声机理、声源识别及控制[J]. 中国铁道科学， 2009， 30（1）： 8690.

ZHANG Shuguang. Noise mechanism， sound source localization and noise control of 350 km/h highspeed train[J]. China Railway Sci， 2009， 30（1）： 8690.

[6]HOWE M S. Theory of vortex sound[M]. Cambridge： Cambridge Univ Pr， 2003： 120.

[7]MHRING W. On vortex sound at low Mach number[J]. J Fluid Mech， 1978， 85（4）： 685691.

[8]李晓冬， 王凯. 高速电梯气动特性研究与优化[J]. 哈尔滨工业大学学报， 2009， 41（6）： 8286.

LI Xiaodong， WANG Kai. Optimization of aerodynamic characteristics of highspeed elevator[J]. J Harbin Inst Technol， 2009， 41（6）： 8286.

[9]鲁国雄. 高速电梯井道通风数值分析[J]. 中国电梯， 2009， 20（14）： 2529.

LU Guoxiong. Highspeed elevator shaft ventilation road numerical analysis [J]. China Elevator， 2009， 20（14）： 2529.

[10]PIERUCCI M， FREDERICK M. Ride quality and noise in high speed elevators[J]. J Acoust Soc Am， 2008， 123（5）： 32473247.

[11]谢多夫. 力学中的相似方法与量纲理论[M]. 沈青， 译. 北京： 科学出版社， 1982： 1