基于遗传蚁群算法的带时间窗多车场车辆调度问题

马洪坤，杨　伟，赵　佳，郝海彬

(西华大学交通与汽车工程学院，四川 成都　610039)



基于遗传蚁群算法的带时间窗多车场车辆调度问题

马洪坤，杨伟*，赵佳，郝海彬

(西华大学交通与汽车工程学院，四川 成都610039)

摘要：给出带单边硬时间窗的多车场车辆调度问题的数学模型，并提出一种遗传蚁群融合算法。该算法在遗传算法的基础上加入蚁群路径搜索和自适交叉变异来提高算法搜索能力，并且采用模拟退火个体接受方式接受蚁群路径搜索产生的新个体，从而使算法提高了跳出局部最优点能力。结合算例计算验证了算法的有效性和正确性。

关键词：遗传蚁群算法； 自适应； 多车场； 时间窗； 车辆调度问题

车辆路径优化问题是一个经典NP难题[1]，该问题是指在已知配送中心、客户位置和需求量的前提下，在满足运输容量和送达时间约束的基础上，规划出一条或者若干条运输时间或运输距离最小的路径。该问题具有比较大的现实意义，现实中很多客户对货物的需求时间都比较严格，因而都可以归结为带硬时间窗的多车场车辆调度问题；但是该问题是一个NP难度问题，一般优化算法难以得到问题的最优解。近年来，遗传算法和蚁群算法等启发式算法在该类问题的求解中得到成功应用[2-4]，但算法优化结果还有进一步提高的空间。

遗传蚁群算法结合了遗传算法和蚁群算法的优点，是一种优化能力较好的启发式算法。本文从遗传自适应搜索和模拟退火向后搜索机制两方面改进该算法，较好地提高了算法的搜索效率和搜索结果。仿真实验表明，该算法在带时间约束多车场车辆调度问题中能得到较好的结果。

1问题描述和数学模型

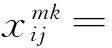
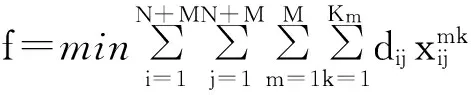
(1)

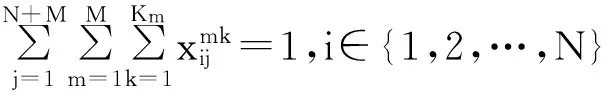
(2)

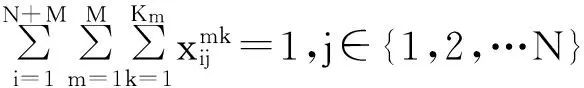
(3)

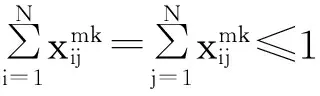
m∈{N+1,N+2,…,N+M}，

(4)

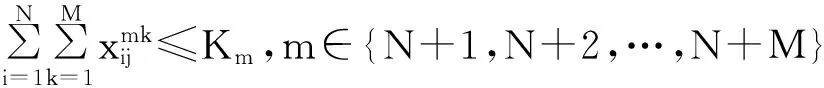
(5)

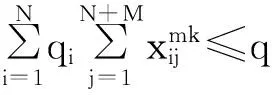
m∈{N+1,N+2,…,N+M},

(6)

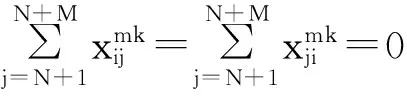
m∈{N+1,N+2,…,N+M},

(7)

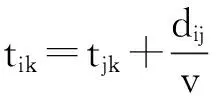
(8)

tik≤Di。

(9)

其中：式(1)为模型目标函数，即车辆运行的最短路径；式(2)、(3)表示每个客户只能被一辆车服务一次；式(4)表示车辆都是从自己车场出发最后返回各自车场；式(5)表示每个车场派出的车辆数目不能超过自身拥有的车辆数目；式(6)表示车辆容量限制，即每辆车的载重量不能超过其载重能力；式(7)表示车辆不能从车场到车场；式(8)、(9)表示货物送到时间满足最晚时间窗约束。

2遗传蚁群算法

2.1算法概述

遗传算法和蚁群算法是路径优化方法中常用的2种启发式规划算法；但是这2种算法对于多车场多车辆调度问题来说都具有一定的局限性[5-6]，主要体现在遗传算法难以得到较好的路径优化结果，蚁群算法难以解决车场对于客户的选择配送。针对这个问题，本文提出一种基于改进遗传蚁群算法的多车场多车辆路径优化算法。该算法首先构建遗传算法优化初始客户分配和初始路径，从而得到初始种群，然后以个体初始客户分配为基础，采用蚁群算法优化初始路径，得到新的个体，比较新个体和旧个体适应度值的大小，如果新个体适应度值优于旧个体，则用新个体取代旧个体，否则以一定概率取代旧个体。

2.2算法改进和步骤

2.2.1染色体编码

遗传算法中每个染色体都是问题的一个潜在解，本文的染色体采用双层编码的方式，在车场数量为M，客户数量为N的前提下，染色体长度为2N，其中1-N代表客户分配方案，N+1-2N代表客户路径优先级，优先级值越小则表示客户越早被车辆服务，然后按照车载能力约束将客户按照服务的优先级加入路径中，如满足车载能力约束则将此客户加入到路径中，否则以此客户为第一个服务客户重新构造路径，直至所有客户都被服务。例如，假设M=2，N=6，染色体为[1 2 1 1 2 2 5 2 3 4 1 6]，该染色体表示车场1对应的客户运输顺序为客户3-客户4-客户 1，车场2对应的客户运输顺序为 客户5-客户2-客户6。客户3、4满足第1辆车的车容量约束，而加上客户1则不满足，则车场1的车辆路径为车场1-客户3-客户4-车场1，车场1-客户1-车场1。

2.2.2适应度函数

适应度函数的计算在解码的基础上按照式(1)计算个体适应度值，适应度值越小，运输时间越短，个体越优。染色体在解码的过程中，首先根据染色体1-N基因位置解码出每个车场分配的客户，再根据染色体N+1-2N解码出客户运输顺序，然后车辆从车场出发把货物依次运送给客户。在运送的过程中，根据式(9)实时计算当前时间，如果一辆车的货物已经全部派送完，则返回后派出下一辆车继续运送。在解码的过程中，需要确保满足客户送到时间约束，采用惩罚函数处理时间约束问题，如果客户达到时间不满足时间约束要求，则在个体适应度上加入一个比较大的值，从而使该个体在进化的过程中被逐渐淘汰，适应度计算方法如式(10)所示。

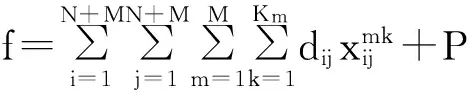
(10)

式中P为惩罚值，满足约束条件下为0，不满足约束条件下为一个极大值。

2.2.3遗传算子

选择算子采用轮盘赌选择方式，个体适应度值越低，被选中的概率越大[7]。交叉算子在随机选择两个交叉个体之后，采用随机初始化交叉位置后染色体基因互换方式进行交叉，变异算法在随机选择1个变异个体之后，采用随机初始化变异位置后基因变异方式进行变异。

在交叉和变异操作中，一般认为被选中参与个体适应度值越差，越应该进行交叉和变异操作，从而能够产生新的个体，适应度值越好，越应该避免进行交叉和变异操作[8]，从而能够把该个体保留到下一代中。借鉴上述交叉和变异操作的思想，本文提出了一种自适应交叉和操作方法。该方法初始化了3个从大到小交叉概率和变异概率调整参数，且Pc1>Pc2>Pc3，Pm1>Pm2>Pm3。在每次选择交叉或变异的个体之后，根据选择个体的适应度值来计算实际交叉概率和变异概率，从而促使适应度值低的个体以更高概率参与交叉和变异操作来产生更好的个体，交叉和变异概率计算公式如式(11)、(12)所示。

(11)

(12)

式中：f′为参与交叉个体中适应度最大值；favg为种群平均适应度值；f为参与变异个体适应度值；fmax是当前种群中染色体适应度最大值；fmin是当前种群中染色体适应度最小值。

2.2.4蚁群算法优化路径

在遗传算法搜索得到客户分配以及运输路径之后，采用蚁群算法优化每个车场配送路径。蚁群优化路径包括个体解码、适应度计算、信息素初始化、状态转移概率和信息素更新5个环节。

个体解码：根据遗传染色体个体解码出每个车场的配送客户和初始配送路径，蚁群算法每次只优化配送路径。

适应度计算：蚁群算法适应度值是每个车场所有客户配送路径长度，如式(13)所示。

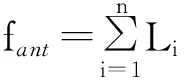
(13)

式中：n是车场分配客户数量；Li为客户间距离。

信息素初始化：信息素矩阵C是蚁群算法搜索依据，按照遗传初始优化结果初始化信息素矩阵，初始路径包含节点对应的信息素较大，从而使遗传优化方案更容易被选择。

状态转移概率矩阵：对于当前节点，蚁群算法选择下一个节点的状态转移概率矩阵如式(14)所示。

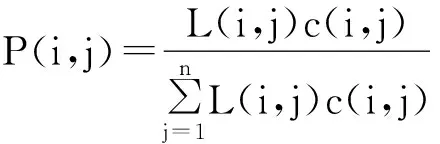
(14)

信息素更新：蚁群算法每迭代一次之后，都按照当前最优路径更新信息素，信息素更新如式(15)所示。

(15)

式中：ρ为信息素挥发速度；Qa为信息素增加量。

2.2.5模拟退火个体采纳

把模拟退火算子引入到遗传蚁群算法中，算法在迭代计算开始时初始化温度T0，该温度在每次迭代中按照一定比例下降，每次蚁群算法生成的个体，都按照模拟退火个体采纳方法判断是否取代原始个体，从而让算法具有跳出局部最优解的能力。模拟退火个体采纳公式如式(16)所示。

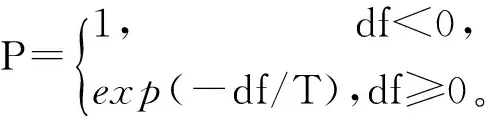
(16)

式中：df为蚁群优化个体和原始遗传个体适应度值差；T为当前模拟退火温度，该温度按照遗传算法迭代以q值速度进行降温。

2.3算法流程

本文构建的改进遗传蚁群算法的计算流程如图1所示。

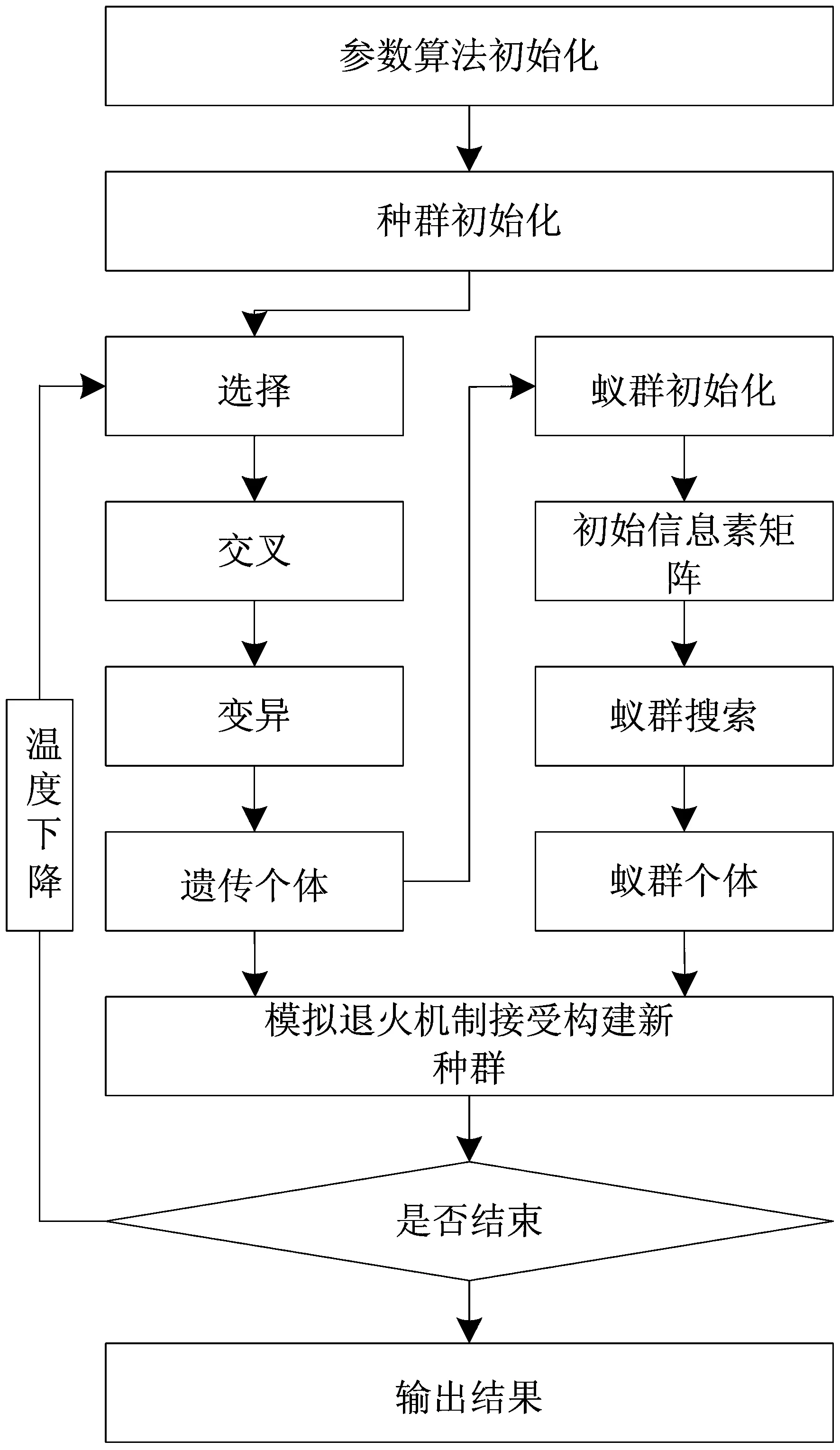
图1　算法流程

3算例分析

采用本文提出的优化算法优化3个车场和25个客户的带时间约束路径优化问题，每个车场都具有5辆运输车辆，每辆车的载质量为20 t，车辆行驶速度为匀速60 km/h，每个客户都有一定的需求量和送达时间要求，车场和客户信息分别如表1、2所示。

分别采用普通遗传算法、遗传蚁群算法和改进遗传蚁群算法优化该问题，问题参数为：遗传算法种群个数为20，遗传迭代次数为100，交叉概率数组为[0.2 0.3 0.4]，变异概率数组为[0.2 0.3 0.4]，初始温度为1 000，温度降温速率为0.9，蚁群算法种群个数为10，蚁群迭代次数为50，优化过程比较如图2所示。改进遗传蚁群的最优结果如表3所示。采用上述3种算法反复计算100次，3种算法的优化结果比较如表4所示。

由图11和图12可以发现，不同开挖深度加载对围护桩的水平位移影响较大。随着基坑开挖深度增大而进行加载，围护桩最大位移逐渐减小，且加载时的开挖深度越大，围护桩最大水平位移减小量越大，基坑未开挖之前进行加载围护桩产生的水平位移最大。因此，在实际工程中，基坑应尽早施工并开挖至坑底，减少斜拱桩基施工产生的大水平推力对深基坑围护桩变形的影响。

从图2、表4可以看出，在使用相同的种群规模、交叉变异参数的条件下,本文提出的改进遗传蚁群算法函数适应度在第20代收敛于1 039，使用遗传算法适应度值在第56代收敛于1 151，使用遗传蚁群算法函数适应度值在第78代收敛于1 073。本文提出的算法收敛速度和优化结果都优于另两种方法。车辆速度为60 km/h，所以车辆行驶时间就等于行驶路程。从表2和表3对照可以看出，计算的优化路径都能使每个客户需求点满足时间窗要求，又因算法本身就满足车载能力约束，所以本算法的结果都能够满足约束条件。本文提出的改进遗传蚁群算法通过加入蚁群路径搜索、退火向后搜索、自适应交叉变异等方法提高了算法全局搜索能力，具有较好的优化能力。

表1　车场信息

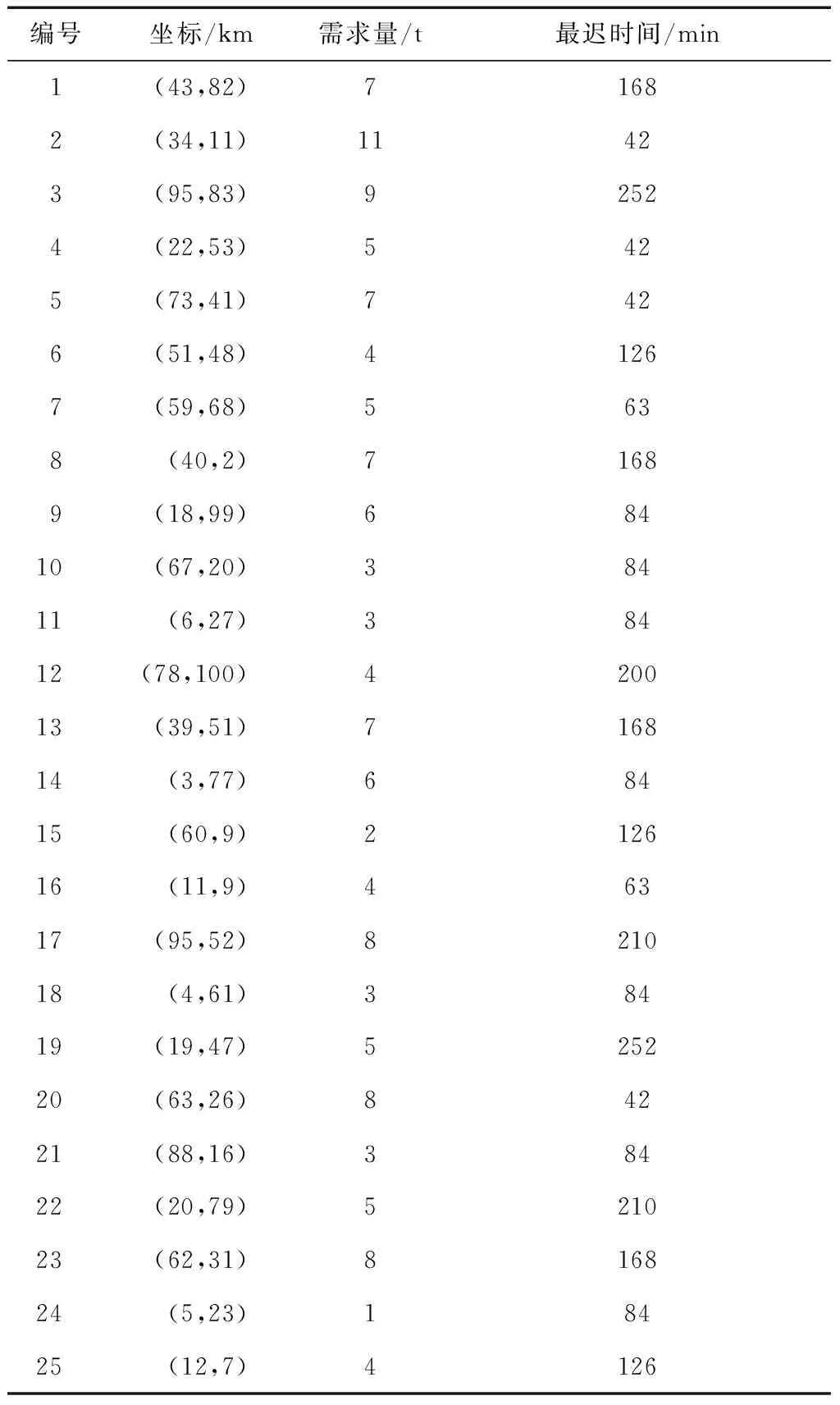
表2　客户信息

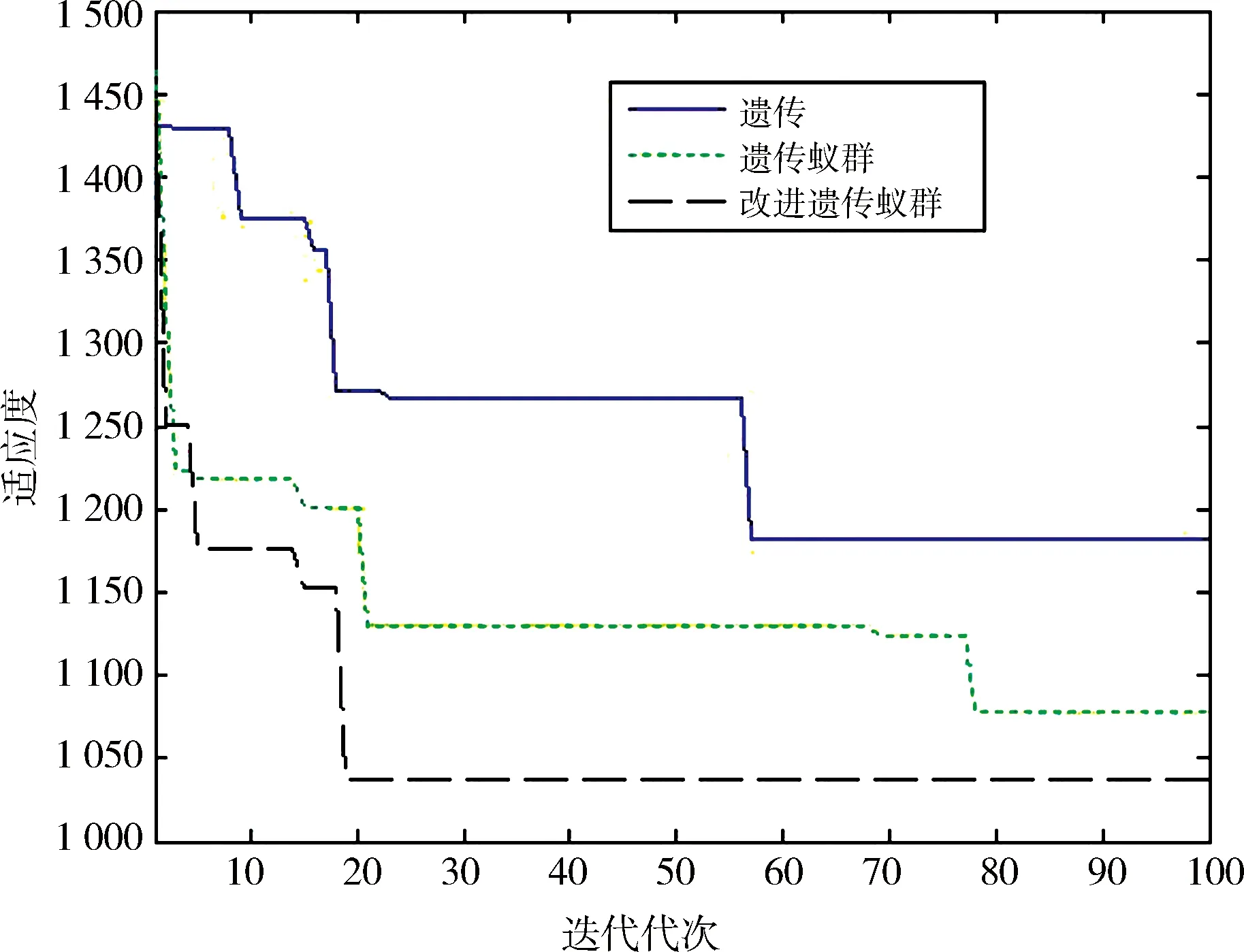
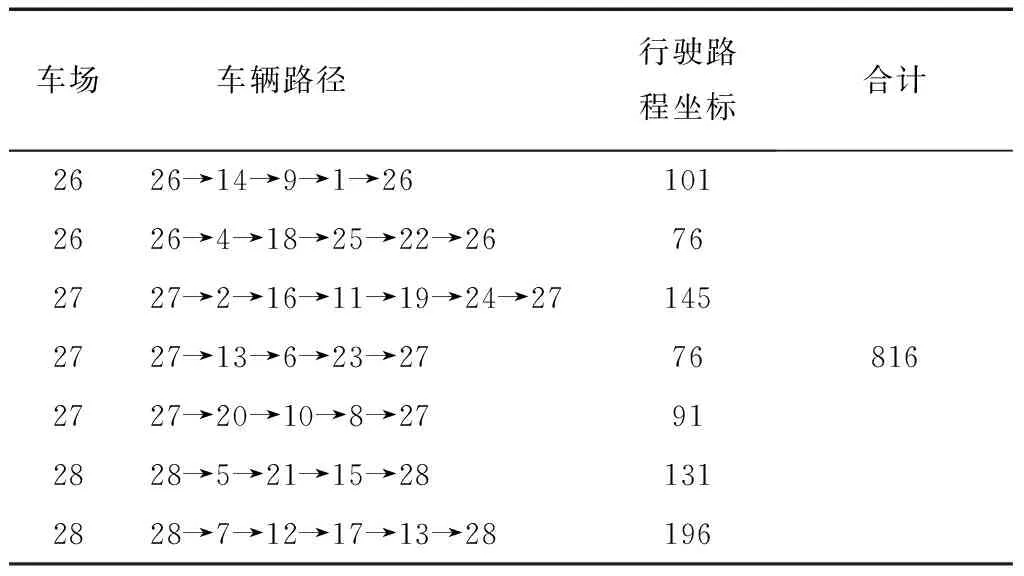
图2　优化结果

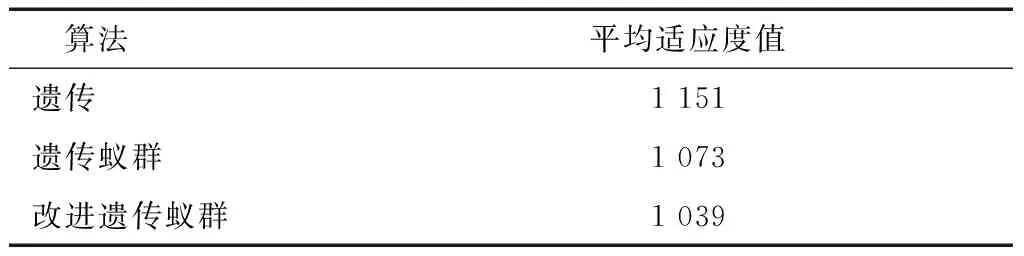
表4　优化结果比较

4结束语

本文根据带时间窗的多车场多车辆路径优化问题的优化难点，构建了一种改进的遗传蚁群算法，通过加入蚁群路径搜索、退火向后搜索、自适应交叉变异算子等方法提高了算法全局搜索能力，并且通过仿真实验验证了该算法的有效性和正确性。

参考文献

[1]李军，郭耀煌．物流配送车辆优化调度理论与方法[M]．北京：中国物资出版社，2001：3-6.

[2]谢秉磊，李军． 有时间窗的非满载车辆调度问题的遗传算法[J]．系统工程学报，2000， 15(3):290.

[3]TAN K C，CHEW Y H，LEE L H． A Hybrid Multi-objective Evolutionary Algorithm for Solving Truck and Trailer Vehicle Routing Problems[J].European Journal of Operational Research，2006，172:855.

[4]蒋毅．基于蚁群优化算法的车辆路径问题研究[D]．长春：吉林大学，2007．

[5]丁建立, 陈增强, 袁著祉. 遗传算法与蚂蚁算法的融合[J]. 计算机研究与发展, 2003，40(9):1351.

[6]刘勇,崔炳谋,王小东,等. 物流配送路径优化问题的模型及改进混合算法[J].物流科技,2008(4):26.

[7]杨元峰．多车场多车型车辆路径问题的改进遗传算法[J]．计算机与现代化，2008(9):10.

[8]占焱发. 基于遗传算法的物流配送车辆路径问题研究[D]. 西安：长安大学，2010.

(编校：夏书林)

Study on Multi-distribution Vehicle Scheduling with Time Window Based on Genetic Algorithm-ant Colony Algorithm

MA Hongkun，YANG Wei*，ZHAO Jia ，HAO Haibin

(SchoolofTransportationandAutomobileEngineering,XihuaUniversity,Chengdu610039China)

Abstract:The multi-distribution centers vehicle scheduling model with a single time window was built in this paper. A new hybrid algorithm combining Ant colony algorithm with genetic algorithm was proposed. In order to improve the Search ability of the algorithm, a colony algorithm and a adaptive for adjusting and mutation probability were combined based on the genetic algorithm. To improve the ability of algorithm to avoid being premature, a way with Simulated annealing algorithm was utilized to accept new member produced by Ant colony algorithm. Finally，the effectiveness and validity of the algorithm were tested through simulation.

Keywords:genetic algorithm-ant colony algorithm; adaptive; multi-depot; time window; vehicle routing problem

收稿日期：2015-11-11

*通信作者：杨伟(1965—)，男，教授，博士，主要研究方向为汽车被动安全技术。E-mail:yw@mail.xhu.edu.cn

中图分类号：U491

文献标志码：A

文章编号：1673-159X(2016)03-0031-5

doi:10.3969/j.issn.1673-159X.2016.03.007

·新能源汽车与低碳运输·