关于『距离』的认识与讨论
2016-06-19宋煜阳
◇宋煜阳
关于『距离』的认识与讨论
◇宋煜阳
关于“距离”,小学阶段主要涉及 “点到直线的距离”“两点间的距离”这两个具体概念。而这两个概念在人教版新教材编排上发生了较大的变化,主要表现为:“点到直线的距离”在四年级上册由原来的依附于“画垂线”调整为单设例题进行教学;“两点之间的距离”新增加在四年级下册 “三角形三边关系”的教学内容之中。可以说,新教材把“距离”这个概念推向了一个核心的位置。那么,教材为什么要重视“距离”这个概念呢?我认为其主要原因是“距离”是平面图形和立体图形中认识“高”概念的基础,如圆锥的高(从圆锥的顶点到底面圆心的距离是圆锥的高)就是以两点间的距离为基础下定义的。作为一个新增的核心概念,对“距离”概念本身的认识与相关教材编排的梳理与讨论还是非常有必要的。
一 “两点间的距离”与“点到直线的距离”哪个概念先学为好
在人教版新教材的编排中,是先教学“点到直线的距离”后教学“两点间的距离”的。“点到直线的距离”这个概念,教材表述为:“从直线外一点到这条直线所画的垂直线段最短,它的长度叫做这点到直线的距离。”“两点间的距离”这个概念,教材表述为:“两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。”从本质上说,两个概念都是一个量数,最终落脚点都是对线段长度的刻画。
从概念的定义来看,“点到直线的距离”是一个发生式定义的概念,有的教材版本描述为“从直线外一点向这条直线引垂线,这点到垂足间的线段长度就是点到直线的距离”,这样描述更为清晰明确。这也就意味着“点到直线的距离”最后化归为“两点间的距离”,即“直线外一点”和“垂足”这两个点之间的线段长度就是“点到直线的距离”,无形之中“两点间的距离”成为“点到直线的距离”的基础。对于学习者而言,用发生式定义描述概念的发生过程时,描述越具体,越容易理解并越容易操作。为此,无论是从概念的逻辑体系还是学习者的学习提高来说,笔者都认为先教学“两点间的距离”更有利于小学阶段对“距离”概念的整体把握。
至于“两点间的距离”这个概念,就相关知识而言,主要涉及线段、折线段、曲线段的区分与度量,突出了线段的特点,可以考虑在“线段的认识与测量”教学内容后开展教学。因为在人教版教材中“线段”概念编排在二年级,这与课标要求第二学段掌握“两点之间线段最短”的这一基本事实有冲突,所以如何合理安排“两点间的距离”这个内容是一个有待深入讨论的重要话题。
二 “平行线之间距离处处相等”的逆命题如何合理解释与运用
教材上对“平行线之间距离处处相等”(以下简称为平行线的性质),原先的描述为“与两条平行线互相垂直的线段的长度都相等”(如图1),后来考虑到学生可能用不完全归纳法得到平行线的性质,于是调整为“端点分别在两条平行线上,且与平行线垂直的所有线段的长度都相等”(如图2),强调了所有线段,确保了知识的准确性和逻辑的严密性。

图1,2013版教材

图2,2015版教材
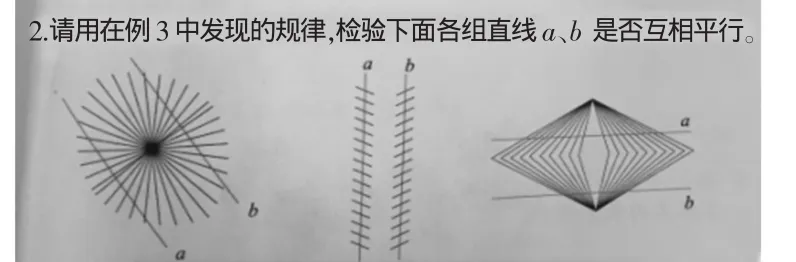
图3,2013、2015版教材
另外,教材在练习中安排了黑林错觉(如图3),意在运用平行线的性质的逆命题对平行线进行判定。问题在于:原命题成立,它的逆命题(如果两条直线之间的距离相等,那么这两条直线互相平行)是否也成立?教材中没有交代,就直接视作已经获取的规律加以运用,在逻辑上似乎讲不通。固然,教材想加强平行线性质的理解与运用,但在平行线判定面前,学生能否用两个命题之间的互逆关系加以运用呢?教学调查显示,很多学生在“平行”概念学习之前,对图4中两条直线是否平行的判断方法采用的是“同一个方向宽度是否相同”的直观经验;而在平行线的性质学习后,也很少有学生能够将这一经验改造、提升为“如果两直线之间的距离相等,这两条直线就互相平行”,即把平行线的性质的逆命题作为平行线判定方法,学生还是存在较大困难的。
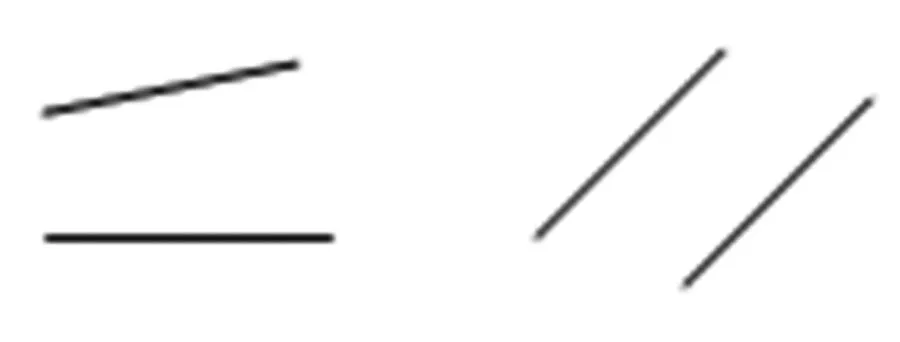
图4
因此,平行线性质的逆命题的存在性及其应用,都是“点到直线的距离”这个概念教学讨论中绕不开的重要话题。
(作者单位:浙江奉化市教师进修学校)
