基于“红花片比蓝花片多几个”的教学思考

◇于正军

基于“红花片比蓝花片多几个”的教学思考

◇于正军

笔者近日听了一节“求两个数相差多少的实际问题”的课。

课堂上，教师一旦出示图1，求红花片比蓝花片多几个，学生便会“无视”教师的“强调”与“强化”，依然用“8+5=13（个）”进行解题，并在集体交流时异口同声地回答“多5个”。究其原因：（1）学生用加法算式解答此问题，说明学生未能体会到求“两数相差问题”的数量关系中所蕴含的减法意义，学生对减法意义的理解仅仅停留在“去掉”的含义上。（2）学生能异口同声地回答“多5个”，那是因为学生通过直观观察这些摆放整齐、清晰的花片后数出来的。即在这一数学活动中，得出的“多5个”与“8+5=13（个）”这个算式之间没有对应关系，“多5个”是学生数出来的。出现这种情况的原因恰恰是教师给予了学生清晰的花片个数，未能激发学生产生有效的数学思考。

故而，教师教学时，需要呈现给学生模糊的信息图，不要出现具体数量的花片图，如图2。

图1

图2

通过观察，激发学生展开有序思考：（1）你能看出是红花片多，还是蓝花片多吗？你是怎么看出来的？（引导学生说出是比出来的）（2）进一步追问：红花片比蓝花片多多少？（课堂上学生此时无语，知道多但无法用语言表达）（3）教师进一步引导：你能指出多的部分吗？学生上黑板指出多的部分后，教师顺势引导：你能给大家指明白一点儿吗？从哪儿到哪儿是多的部分？为什么这部分就是多的呢？（引导学生说出另一部分是和蓝花片同样多的）（4）教师紧接着追问：这部分是多的，那另一部分就是……生：和蓝花片同样多的部分。（5）教师趁势点拨：要求红花片比蓝花片多几个，只要从红花片中把哪一部分去掉？生：把左边部分去掉。师：这部分的个数与谁的个数相同？生：蓝花片的个数。师：所以，要求红花片比蓝花片多几个，只要从红花片的个数里把谁的个数去掉？（6）教师引导学生共同得出结论：要求“红花片比蓝花片多几个”就是要从红花片个数里去掉蓝花片的个数。这样教师只呈现给学生模糊的图形信息，学生根本无法用具体的数列出无效算式，而是在教师的引导下展开有效的、积极的数学思考，去探索“两数相差多少”的数量关系，形成解决此类问题初步的方法模型。

学生通过观察和思考，初步感知了两数相差多少的数量关系后，教师顺势在课件上引出红花片和蓝花片的清晰实物图，学生争先恐后抢着列式解答，为了满足学生的学习需求，促进全体学生理解两数相差关系中所蕴含的减法的意义，并掌握利用减法算式解决两数相差关系的数学问题，教师利用课件不断变化红花片和蓝花片的个数，引导学生进行抢答。此时学生都是用红花片的个数直接减去蓝花片的个数，没有学生再次出现用加法算式列式解答的现象。

在利用清晰的花片实物图抢答的时候，为了使学生在解决问题的过程中，逐步建构两数相差关系的数学模型，教师教学时要巧妙利用课件隐去具体的、可数的实物图形，只留下一些诸如示意图、数学符号或语言文字等“模糊信息”，引领学生在这些“模糊信息”中探寻数量关系的共性特征，掌握解决问题的基本技能。

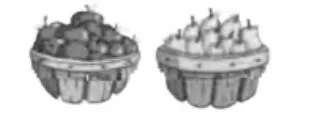
图3

图4

例如：（1）如图3，苹果比梨多多少个？（2）如图4，红彩带比绿彩带长多少？（3）哥哥比弟弟大几岁？所有这些图形、符号以及文字中所隐含的“多与少”“长与短”“大与小”等相差关系都是呈现给学生模糊的信息，没有呈现具体清晰的数量，学生无法直接得出两数比较的结果，必须列出相应的数量关系式。因而，学生在如此“模糊”的信息中必须寻找题中共同的结构特点以及探索统一的解题方法的规律。即，通过探索明白：要求“苹果比梨多多少个”就用苹果的个数减去梨的个数，要求“红彩带比绿彩带长多少”就用红彩带的长度减去绿彩带的长度……此时，教师顺势促使学生主动建构模型，助推学生解题技能的形成。引出诸如：要求○比□多几个、大数比小数大多少，可以怎样直接列式解答？引导学生直接列出算式：○－□，大数－小数。引领学生经历这样的探索过程，学生不仅对两数相差多少的数量关系的思考方法以及解题思路有了切身的体验与深刻的理解，而且可以直接用减法算式来表示两数相差关系的意义，学生的数学学习就会从教师反复强调的被动接受转化为学生自主探索的主动内化。学生对数学知识的建构就会经历从直观图形的感知到符号语言的抽象过程，实现了数学认知的“模糊”到数量关系的本质“彻悟”。

（作者单位：江苏扬州市江都区实验小学）