“联络方式”教学实录及思考

◇施银燕

“联络方式”教学实录及思考

◇施银燕

教学内容

北师大版教材六年级上册“数学好玩”单元中“联络方式”。

教学实录

一、情境，问题

师：早上，天气突变，下起了暴雪。为了安全，学校紧急通知停课。网络全部中断，只能靠电话联系。张老师要通知到全班42名同学，电话需要怎么打？

生1：张老师按全班的学号顺序，一个接着一个打，一共打42个电话，就通知到全班同学了。

生2：我觉得可以是张老师通知1号，1号再通知2号，2号通知3号……最后也能通知到全班同学。

生3：如果要省时间的话，可以把全班同学分组，比如分成6个组，每组7人，每组一个组长。张老师只要给6个组长打电话，再由组长通知组里的其他6个人。

师：紧急通知，往往希望能在最短的时间内通知到全部同学。现在只有张老师一人知道了停课通知，如果打一个电话需要1分钟，通知到全班42名同学，最少需要几分钟？独立思考后再交流。

二、探究，交流

（5分钟后全班交流）

组1：（实物展台展示图1）我们的方案是先把全班同学分成2大组，每组21人。第一次，张老师先打给2个大组长，需要2分钟；每个大组除组长以外有20人，再分成2个中组，每中组10人，第二次，大组长打电话给2个中组长，需要2分钟；这时只需要通知每个中组的其他9个人了，再把9人平均分成3小组，第三次，中组长打给3个小组长，需要3分钟；最后小组长再通知组里的另外2人，需要2分钟。一共要9分钟。

图1

生2：你们确定这是最省时间的方案吗？

组1：我们发现，分的层数越多，需要的时间就越少。我们就想到每次都只平均分成2个组，除了一次是9人没办法这样分，才分成3个组。我们每次都让组数最少，这样层数就最多，所以我们认为9分时间是最少的。

师：组1的方法是不是用时最少，暂不讨论。大家从组1的发言里学到了什么？

生3：他们在探究过程中能发现规律：分组分的层数越多，需要的时间就越少。

生4：用图表示打电话的过程，非常清楚！

师：大家说得真好！在研究过程中，组1善于思考和发现，真棒！

组1：请组2来补充！

（一个学生说，另一个学生在黑板上画图，如图2）

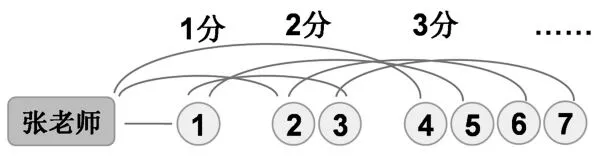
图2

组2：我们的方法是：第1分钟，张老师通知①号同学；第2分钟，张老师通知②号，①号通知③号；第3分钟，张老师通知④号，①号通知⑤号，②号通知⑥号，③号通知⑦号……就这样画下去，我们发现，最后只要6分钟，就能通知到全班所有同学。

生1：我不明白6分钟是怎么来的，你们才画到第3分钟，通知了7名同学。

组2：第1分钟，通知了1名同学，第2分钟通知了2名同学，第3分钟通知了4名同学，大家发现规律了吗？

（学生恍然大悟，明白了第4分钟通知8名同学，第5分钟通知16名同学，第6分钟通知32名同学，6分钟后，接到通知的人数是1+2+4+8+16+ 32，超过了42，所以答案是6分钟）

生2：（询问）哪个小组用的时间比6分还少？

组2：（有点儿犹豫）我们认为这是最省时间的，我们的安排是：凡是得到通知的人，都要不停地打电话通知其他人，一点儿都没有浪费。

师：感谢生2的问题带给大家的思考！回顾组2的方法，你最欣赏哪一点？

生2：他们的思考有序。

生3：他们组找到答案后还不满足，而是寻找规律。

生4：他们能跳出常规分组的想法，从“怎样最不浪费”想起。

师：跳出常规思路，从总的原则想起，总结得好。

生5：我想给他们组的图改进一下。（边说边跑上讲台）在找规律时，已经不用考虑学号了，只要考虑每分钟能通知几个人就行，所以，我觉得图这样画更好！（如图3，把黑板上的连线、学号和“张老师”擦掉，只留下外面的圈）这样图变得简单，更容易发现规律。

图3

师：没错！重要的是第几分钟，有几个人接到电话，也就是时间和接电话人数之间的关系。把不重要的扔了，重要的规律就会水落石出！

（师边说边分别指着1分、2分、3分、4分，学生默契地喊：1人、2人、4人、8人。

师：你们说的1人、2人、4人……是什么人数？

生1：是这1分钟新接到电话的人数，不是接到电话的总人数。

师：发现了什么规律？

生2：每分钟新接到电话的人数都恰好是上1分钟的2倍。

师：有了这个规律，问题就很好解决了，只要看什么？

生3：只要看1+2+4+……加到几等于42人。

生4：我给你纠正一下，不是等于42，如果小于42，就得再加一个数，一定要等于42或者大于42才可以。

生5：我提醒大家，这道题是1+2+4+8+16+32大于42，一共加了6个数，所以是6分钟，不要以为加到32，就是32分钟了。

师：找到每分钟新接到电话的人数规律，问题就迎刃而解了。同学们，我们的问题是几分钟能通知到全班42人，从这个问题出发，找找接到通知的同学总数的变化规律，你有什么发现？

生6：1分钟，有1名同学知道；2分钟，有3名同学知道；3分钟，有7名同学知道。它们的规律是1×2+1=3，3×2+1=7，每次都是“乘2加1”，4分钟能通知到7×2+1=15（人），5分钟通知到15×2+1=31（人），6分钟就是31×2+1=63（人）。所以需要6分钟。

师：从不同的角度观察，同一个方案，能发现不同的规律。想一想，为什么会有“乘2加1”的规律？

生7：因为上1分钟知道通知的同学，每人打一个电话，这样去通知的同学数量就会翻倍，再加上张老师也打了一个电话，所以要加上1人！

师：思考越深入，越觉得有趣！

生8：我觉得“乘2加1”的规律有点复杂，干脆把张老师也看成1名同学，一开始有1名同学通知，1分钟后有2名同学知道，2分钟后就变成4名同学知道，每分钟知道通知的同学都是上1分钟的2倍。也可以说第几分钟，知道通知的同学人数就是“几个2相乘”。这个规律更加简单！

师：如果这样想的话，问题可以修改成什么？

生：全班一共43人，最少需要几分钟？

三、总结、延伸

师：一个问题成功解决了，按惯例，该做什么了？

生1：先回顾总结，再提出新问题。

师：好，下面的时间交给大家！

（师示意生1组织）

生1：同学们，回顾刚才我们解决打电话问题的整个过程，你学到了什么？

生2：遇上一个复杂的新问题，可以先从简单的想起，画图表示，哪怕一开始方法很笨，但只要不断改进，忽略不重要的，就能找到规律。

生3：问题解决的过程中，不能满足于得到一个答案，一定要想想规律和方法，还要想想为什么。

生4：要学会从不同的角度想问题，才能找到最简单的方法。

生1：大家总结得都很好，收获也很多。下面到提出新问题的时间了。

生5：如果需要通知100人，那么最短需要多少时间？

（生1在原来42人下面用红粉笔写上100人，并在前面标上①）

生6：如果每打一个电话需要2分钟，其他条件不变，那么最短需要多少时间？

（生1在黑板上写道：②一个电话2分钟）

生7：如果保证大家得到充分休息，每人打一个电话后都要休息1分钟，其他条件不变，那么最少要几分钟？

（生1在黑板上写道：③打一个电话后休息1分钟）

生1：问题都很有水平！看看哪些问题能解决？

生8：我觉得问题①和原来的差不多，只要按照刚才的规律往下想……

生1：大家都会举一反三！问题③有会解决的吗？

生9：问题③有点复杂，从第1分钟开始，把每分钟接到电话的人数表示出来，再找找规律，应该是能解决的！

师：是的，不管问题怎么变，从最简单的想起，找到了规律后，答案就会有！

师：佩服生7，提出有水平的问题！我把你的问题修改简单些，如果从张老师开始，每个接到电话的人，都先要用1分钟整理电话记录，再打电话。其他条件不变，请问，通知到全班42人，最少需要几分钟？

（学生独立探究，片刻后一些学生窃窃私语：“兔子数列”，面带不可思议的神色）

师：发现了什么？

（有6名同学情不自禁地喊道：兔子数列）

生1：我找的是每分钟知道消息的人数的变化规律！

生：（七嘴八舌）1分钟有几人知道消息？写上1分钟，2分钟，3分钟……

师：就按大家说的，我先写上1分钟，2分钟，3分钟……一开始，只有张老师1人知道消息，（板书1人）1分钟后有几人知道消息？

生：2人！（也有人喊）还是1人。

师：有不同意见了，说说理由。

生2：因为张老师先要用1分钟整理电话记录，不能打电话，所以1分钟后还是只有张老师一人知道消息。

生3：他说得对，我没考虑这一点，应该是1人。

师：把想法说出来，就能看出谁的有道理，也能发现问题所在，这才是交流。

（师板书：1人）

师：2分钟呢？

生3：有2人，这时张老师通知了1人。

生4：3分钟后有3人知道了，因为只有张老师可以打电话，第一名同学还要整理电话记录，所以只能增加1人。

生5：4分钟后增加2人，因为张老师和第一名同学都能打电话。所以1、1、2、3、5……正好是兔子数列！

生6：我认为你的结论下得有点儿早，最好再往下看看。

生5：往下看也符合这个规律。第5分钟，正好是张老师和前两名同学都可以打电话，所以就增加3人。

师：目前为止，这个新的问题解决了吗？

生：我们发现了每分钟知道通知的人数正好是兔子数列，只要按兔子数列写下去，看几分钟时人数达到43就可以了。

师：有什么感受吗？

生1：太神奇了！打电话居然能和兔子数列联系在一起。

生2：这个规律恰好是兔子数列，不是巧合，而是有道理的。

师：同学们，问题就是这样，你觉得它难，它就会躲着你；反过来，你越琢磨，就会越觉得它有意思。这个兔子数列，还有一个名字叫斐波那契数列，是以一位数学家的名字命名的。课后同学们可以对这个数列好好研究一下，如刚才那个数列1、2、4、8、16……前后两项的比值始终是，那么这个兔子数列呢？查阅一下资料，更多的神奇会等着你。

教学反思

组1的打电话方案并不在我的预设里。一开始，我对这一方法是不屑的，“张老师通知大组长、大组长通知中组长、中组长通知小组长”，一看就不省时。但在学生的追问下，他们叙述的思考过程非常有价值！我想，面对学生的不同想法，教师采取更为理解、欣赏的态度，才会有通畅且有质量的交流。

总结延伸阶段，把学生提出的问题，进行了简单改造：先做1分钟的电话记录，再开始打电话。这样就把规律变换成了“斐波那契数列”模式，这也是瞬间迸发的灵感。或许有老师会有疑问，斐波那契数列，是否过于高深？课堂上探究这样的问题是否“不务正业”？我想，如果学生有画图意识，有从简单问题想起的转化思想，有探究规律的能力，问题难易的边界已模糊。

课后花絮

真实而又有数学味的问题引起了学生极大的兴趣，课后的探究也格外充分，还有一项副产品让我偷着乐：计算斐波那契数列前后项比值时，许多学生的竖式写了满满好几页，不知不觉中练习了不少小数除法。同学们交流的许多斐波那契数列的规律，更让我吃惊，而由斐波那契数列带出的黄金分割数则让学生赞叹，知识之间的神奇联系让学生着迷！

（作者单位：北京市北京第二实验小学）