三角函数章节案例有效解答之探析
2016-06-18刘凤
刘凤
摘 要: 案例教学是不同阶段数学学科教学的重点,同时也是其需要着力主攻的难点和薄弱点。本文就三角函数章节案例的有效解答这一话题,从三个方面做了探析。
关键词: 三角函数 案例教学 有效解答
三角函数章节是高中阶段数学教材架构体系的构建“枝干”,同时也是教师讲解、讲授等实践的重点和难点。三角函数章节内容是初中阶段函数知识内容的“升华”,同时也是高等数学函数章节知识的“基石”,其作为一种基本初等函数,在解决生产、生活等实际问题中运用广泛。常言道:根基牢,地动山摇稳不倒。要达到科学、高效解决现实问题的目的,就必须“打基础”、“重训练”,强化书本数学习题解答的有效训练。案例教学是不同阶段数学学科教学的重点,同时也是其需要着力主攻的难点和薄弱点。而案例解答的现实意义和长远功效已经被教学工作者所共识。笔者现就三角函数章节案例的有效解答这一话题做探究和分析。
一、三角函数案例解答应注重师生深入互通,体现双向性。
教育运动学说认为,案例的讲授是课堂实践体系的重要环节,是课堂实践进程的重要部分。案例的讲解应该体现并传承课堂教学的双边特点和双向特性,师与生对等交流、生与生合作探讨等多向、多边活动应渗透并融入在其中进程。但在实际的案例教学中,教者的个体讲解或学习主体的自行探索的单向问题不同程度地存在。因此,在三角函数案例解答中,教师要正确处理好师生之间的关系,将自身的引导功效发挥出来,组织和引领高中生进入到三角函数的案例讲解研析中,紧扣问题要解决的要求、思路的确定及方法的甄别等都需要深入互动、讨论,在深入的双边互通中,达到探究实效、共进互赢的期望。
如在“如图所示,α、β分别是坐标轴上的一个角,其度数分别是30°和300°,OM,ON分别表示角α和角β的终边。(1)分别求出与α,β两个终边的相同角集合;(2)求出始边在OM的位置,终边在ON位置的所有角的集合。”案例讲解中,教者实施互动式讲解活动,主要围绕在表示角的度数时,如何做好角度制或弧度制之间统一的话题,组织高中生开展解答问题活动。教者根据所出示的数学问题及要求,在他们自主研析的基础上,与他们围绕思路的确定及过程的确认进行双边探讨活动,一起分析研究解题思路,一起辨析解题过程,并明确告知他们,找出在[-π,π]范围内与α、β都有相同的角度,再根据任意角的概念和角集合的表示法,可写出终边落在阴影部分(含边界)时所有角的集合。同时在解决上述两个问题时要切实注意角度制和弧度制之间的同一性问题。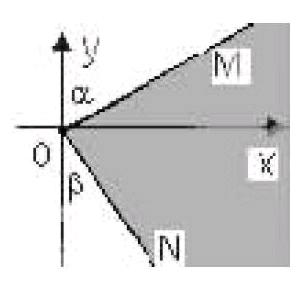
二、三角函数案例解答应注重讲练融会贯通,体现发展性。
教者是主体进程实践中的“引路人”,探究疑惑的“释惑者”,以及认知探索的“推进者”。教者的一项任务,就是通过有效、精准的“导引”形式,有力地推动他们开展探知和研析活动。高中生在研究、分析、探寻三角函数案例的进程中,会遇到许多“超越”自身学习实际能力的要求和标准。此时,教者就要发挥指导功效,在他们的解决三角函数案例的“练习”中,实施有效指导,弄清题意,理清层次,点明联系,从而确保三角函数案例解题深入推进。在此过程中,教师的“讲解”和学生的“练习”二者不是分割、不衔接的,而是联系、相贯通的,成为讲练合一的有机整体。
问题:已知角α终边上有一点P,它的坐标为(x,3)(x≠0),并且cosα=3/10x,求sinα和tanα的值。
学生进行解析实践:根据题意可知,这是关于三角函数与方程方面的综合性运用题,涉及三角函数的定义等内容。
教师适当点拨:在该问题中,要求出sinα和tanα的值,还是要求出点P的坐标x,同时要注意α所在象限的位置进行讨论。
学生围绕解题要求进行思路完善,并着手进行该问题解答活动。
教师强调:关键要注意α所在的象限不确定时要采取分类讨论的方法采用研析。
高中生按照教师点拨和强调,开展合作提炼解题方法活动,得出其解法。
三、三角函数案例解答应注重解析方略提炼,体现策略性。
在解析上述案例基础上,总结提炼环节,组织他们对刚才获得的解题思路及过程进行“回味”和“思索”,要求他们对其所确定的策略进行提炼和总结。高中生结合所得思路及所解过程,认识到:“该问题借助三角函数内容,运用到数形结合的思想策略。”高中生在教师有序引导下认识到:“该问题解答中,通过函数的图像性质及三角函数函数区间的求解实现了有效解答,这其中蕴含了数与形结合的解题方法。”
教师因地制宜,围绕“数形结合”解题思想进行专题讲解活动,对该解题思想的本质及注意事项等进行明确说明,并向高中生指出其在三角函数章节中的运用,并展示案例进行巩固强化,从而让高中生对该解题思想有切身、具体、深刻的认识和掌握,提高其解题技能和素养。
通过上述三角函数问题的讲解活动,高中生对解题思想方法运用有了更深刻的认知和运用。教育学指出,教学的目的在于传授技能及技巧,提高自主学习能力。因此,教师无论在三角函数章节,还是其他数学学科章节中,问题解答活动的讲解,应注重对解题方法或策略的讲授,对典型数学内容的应用,以题讲解,让他们通过亲身探究、实践和辨析,对其有感性认知。同时借助于教师的科学专题讲解,对其内涵、特点及事项等方面深层次掌控,深层次地认知和掌握知识,保证在其方法策略运用中自如、高效、科学。
教师应强化课堂活动进程中问题解答的组织和推动,注重内在能力素养的培养,将数学解题变为主体前进和发展的“跳板”,开展精心教学实践。
参考文献:
[1]刘文强.浅谈高中数学的三角函数教学[J].数学学习与研究,2014(09).
[2]朱国宗,张宝华,姜林.在讲学习中不断提高思维能力(摘编)[J].湖北社会科学,2000(S1).
