从一道例题说起函数问题

杨婷+王志

本题选自沪教版初中数学八年级第二学期第二十章一次函数内容中《一次函数的图像》第三课时中的一道例题.

例6.已知函数y=2/3x+1.（沪教版数学八年级第二学期P10）

（1）当x取何值时，函数值y=5？

（2）当x取何值时，函数值y>5？

（3）在平面直角坐标系xOy中，在直线y=2/3x+1上且位于x轴下方的所有点，它们的横坐标的取值范围是什么？

下面笔者从三个角度进行关注：

1.以学定教，把握更精准的例题目标

《中小学数学课程标准》中所提出的数学课程目标，是指各学段终结时的目标；在教学过程中，还要确定每个教学阶段的具体目标，直至每节课的学习目标，由此构成形成性的学习目标.我们再将每节课的教学目标细化到每道题的教学目标，评价先行，以学定教.

从整个初中数学的学习体系来看本例题所涉及的知识点，其在不同层面的目标分别是：

《课标》目标：建立一次函数、二元一次方程、直线之间的联系.

单元目标：能借助一次函数的图像认识一元一次方程的解、一元一次不等式的解集，理解一元一次方程、一元一次不等式与一次函数之间的内在联系.

课时目标：知道一元一次方程、一元一次不等式与一次函数之间的联系，能以函数的观点认识一元一次方程的解与一元一次不等式的解集；通过研究一元一次方程、一元一次不等式与一次函数之间的联系，体会数形结合的数学思想，初步领略用函数知识分析问题的方法.

通过研读目标，我们将这道例题的目标和功能进一步细化：

A层目标：

（1）会从代数的角度思考问题，用式的代换和运算解决；

（2）通过观察函数图像、求方程的解和不等式的解集，体会一元一次方程、一元一次不等式与一次函数的联系；

（3）会用图像法解一元一次不等式；

（4）能利用一次函数与一元一次不等式的内在关系，解决实际问题.

B层目标：

（1）会从代数的角度思考问题，用式的代换和运算解决（达标率100%）；

（2）通过观察函数图像、求方程的解和不等式的解集，体会一元一次方程、一元一次不等式与一次函数的联系（达标率75%以上）；

（3）会用图像法解一元一次不等式（达标率75%以上）.

2.因材施教，深入更严谨的教材教学

本节课的知识要点是新教材中后添加的内容，不仅是应试的重点考察对象，而且是帮助学生进一步感受数形结合的数学思想重要途径之一.本节课也是在学生已有对一元一次方程、一元一次不等式和二元一次方程组等的认识之后，从变化和对应关系的角度，对一元一次不等式的运算进行更深入的讨论，是站在更高起点上的动态分析.通过讨论一次函数与方程（组）及不等式的关系，用函数的观点加深对这些已经学习过的内容的认识，加强知识间的横向和纵向联系，发挥函数的统领作用，构建和发展相互联系的知识体系.

于是，我们备课组设计一道检测拓展：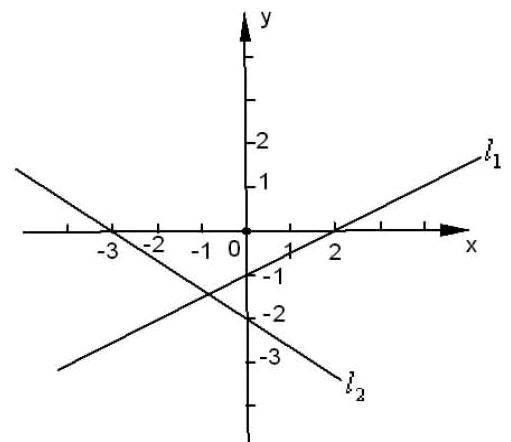

已知一次函数y=k1x+b1和y=k2x+b2的图像分别是直线l1和l2，根据图像填空：

（1）方程k1x+b1=0的根是______________；

不等式k1x+b1<0的解集是______________.

（2）不等式k2x+b2>0的解集是______________；

方程k2x+b2=-2的根是______________.

这道检测题目的设计源于拓展依据的综合处理，检测题目的难度要求要高于例6，它可以从数和形两方面进行检测对代数方法和图像直观法的理解.

3.以学促教，理解更贴切的实际学情

例6是在一次函数与一元一次方程的基础上展开的，学生理解了一次函数与一元一次方程的关系，进一步体会数形结合的基本思想，并初步有了用函数的观点考查教学问题、解决教学问题的思想.函数、方程、不等式都是刻画现实世界中量与量之间变化规律的重要模型.本节的目的就是通过具体例子渗透三者之间的内在联系，帮助学生从整体上认识不等式，感受函数、方程、不等式的作用.在教学过程中注意引导学生初步体会从整体中把握部分的思维方法，渗透函数、方程、不等式思想和数形结合等重要的数学思想，拓宽学生视野，相信学生并为学生提供充分展示自己的机会.

回归本源，张奠宙教授早就提出“教什么永远比怎么教重要”.数学教育面临两大问题：

（1）教什么——教学内容

（2）怎么教——教学方法

内容和方法是紧密联系的，只有肯定了“教什么”，才能研究“怎么教”的问题.这也恰恰就是把握教学目标.尊重教材，真正领会编者的意图.我们的教学目标如果重形式轻实质，那么教什么就失去了方向.一节课的生命力依赖于《课标》的正确解读、对教材的深刻把握和对内容的深刻理解，然后我们才可以按照自己的理解，更深入地理解教学、理解学生、根据实际整合教材，做到更贴切学生实际，这才是本质，才是数学教学原汁原味的本色.