基于Peridynamic理论的硬质合金刀具微观破损预测*

蒋宏婉　何林,2　樊淋　赵先锋　占刚

(1.贵州大学 机械工程学院， 贵州 贵阳 550025； 2.贵州师范学院， 贵州 贵阳 550018)

基于Peridynamic理论的硬质合金刀具微观破损预测*

蒋宏婉1何林1,2樊淋1赵先锋1占刚1

(1.贵州大学 机械工程学院， 贵州 贵阳 550025； 2.贵州师范学院， 贵州 贵阳 550018)

摘要：破损是刀具失效的重要形式之一，传统的刀具破损分析主要是通过切削试验进行，不仅成本高且周期长.文中基于Peridynamic(PD)理论——近场动力学理论，重点研究硬质合金刀具车削42CrMo大直径石油管道过程中刀片主切刃的近域微观破损问题.首先对该切削过程进行有限元仿真分析，从中提取刀具所受载荷；然后根据PD理论，在Visual Studio环境下采用C语言编写近场动力学建模和分析程序，结合Matlab图像处理单元，实现了刀具主切刃近域材料微观破损过程的数值分析，包括裂纹萌生的起始位置、材料质点不同方向的位移趋势、裂纹的扩展趋势等.结果表明，基于PD理论的硬质合金刀具微观破损数值分析方法能够揭示该刀具主切刃近域材料的微观破损机理和破损扩展过程，给定工况下的刀具微观破损主要由冲击载荷引起的与前刀面法向呈一定夹角的微裂纹所导致，并有向里层材料非连续扩展的趋势.

关键词：近场动力学；硬质合金刀具；微观破损；数值分析；预测

金属切削加工中，受机械应力和冲击作用，刀具破损是其常见失效形式，尤其脆性较大的刀具进行断续切削或加工高硬度材料时，刀具破损更加严重.传统的连续介质理论假设材料构型中任一点附近存在连续可微位移场，可有效求解其在弹性阶段的力学行为，但当构型中存在破损时，该理论难于求解.Peridynamic(PD)理论即近场动力学理论采用积分形式描述材料构型的基本运动，避免了对位移场的求导，对于求解刀具材料微观破损等不连续问题具有独特优势.

纵观国内外该领域研究现状，与国外相比，国内研究甚少.在刀具微观破损研究方面，杨明伦等[1]提出了一种基于噪声辅助经验模态分解和本征模函数能量分布的刀具破损识别方法，结果表明，此方法能够剔除切削参数变化的影响，准确识别刀具破损；贺晓辉等[2]提出了一种基于机床加工功率特征信息和互相关算法的刀具破损在线监测方法，结果表明该方法在几种典型刀具破损在线监测中能准确识别刀具失效，具有一定实用性；以上研究重点都在于刀具破损真实产生后的识别和监测，鲜有刀具破损预测方面的研究.在PD理论应用研究方面，沈峰等[3]概述了PD方法的理论基础，描述了其建模思路及计算体系，给出了用近场动力学方法模拟结构受冲击载荷的计算格式，结果表明PD方法可以很好地模拟材料结构的损伤积累与渐进破坏过程；胡祎乐等[4]提出一种基于近场动力学理论的纤维增强复合材料层压板渐进损伤分析方法，构建了适用于各向异性材料的对点力学函数，预测结果与试验结果吻合良好.Weckner等[5]通过比较PD理论中均匀变形的弹性能量密度与经典弹性理论中相应的能量，呈现了如何建立试验测量而来的材料特性(如泊松比和杨氏模量等)之间的联系；Yu等[6]针对某文献中PD数值积分方法的不足，提出了PD理论数值积分的新方法，他们将连续物质离散成离散立方单元，并对单元的不同几何结构和相互作用的层位进行了详细分类，最后通过数值试验案例证明了该方法的精度；Weckner等[7]开发了一个基于高斯β-Hermite求积的非局部一维动力响应有效数值模拟方法，并计算了两个相应的连续与非连续实例，结果验证了该数值模拟方法的正确性； Ghajari等[8]提出了一种各项异性的动态断裂分析材料模型，该模型能够预测复杂的断裂现象，如自发裂纹萌生、裂纹分支以及基于PD理论的键能等，实验证明该模型具有准确模拟多晶结构(如氧化铝陶瓷等材料)动态断裂的能力.以上研究多为PD理论在混凝土、陶瓷等材料上的应用，未见采用PD理论对硬质合金刀具进行离散微观破损预测分析.

根据金属切削理论，刀具破损大都是不连续的，且离散程度据实际切削情况而定，一般的有限元分析方法很难客观分析刀具的非连续破损问题.文中将近场动力学理论应用于刀具微观破损分析，提出一种基于PD理论的硬质合金刀具微观破损数值预测分析方法，该数值方法适合于处理非连续介质力学问题，通过参考域内材料质点的位移情况来间接衡量破损的产生和扩展，可用于求解硬质合金刀具切削加工时刀片主切刃近域材料在从连续体到非连续体的动态演变过程中的破损问题，以预测给定切削条件下硬质合金刀具的微观破损情况.

1刀具破损与近场动力学概述

1.1刀具破损

使用硬质合金、陶瓷等硬度高、脆性大的刀具进行切削，尤其是断续切削时，由于机械和热冲击，刀具时常发生形式不同的破损[9]，主要包括崩刃、裂纹、碎断以及剥落.

1.2近场动力学理论

21世纪初，Silling[10]首次提出近场动力学(PD)思想，该理论有别于传统局部模型位移偏微分方程求解模式，结合分子动力学(MD)、无网格法(MF)和有限元法(FEM)的优点，采用基于非局部思想直接积分形式的运动方程，通过积分对在一定近场范围内具有相互影响的材料点之间的相互作用力进行解算，而不论位移场的连续与否.

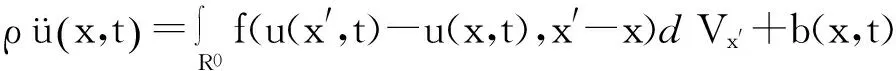
(1)

式中，t≥0，ρ为材料密度，u为材料质点位移场，b为外力的体积力密度，Vx′为质点x′的体积.

定义L(x,t)为内力的体积力密度，表示为

∀x∈R，t≥0.

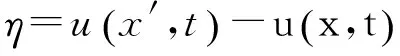
(2)

其中，c表示键刚度常数，与材料弹性模量E和参考域半径δ有关，定义如式(3)所示：

(3)

μ(t,ξ)表示一个定义键失效条件的标量函数，s(η,ξ)表示键的伸长率，可定义为

(4)

当μ的值为1时，表示一个完整的键；当μ的值为零时，键的伸长率达到极限伸长率s0，材料点对间不再有相互作用，键发生永久断裂[15-17].在某一时刻t，材料在质点x处的破损程度可由完整键所占比例φ(x,t)表示：

(5)

2硬质合金车刀的PD数值分析

2.1切削过程数值模拟数据的提取

本研究采用成都工具所的硬质合金车刀切削石油管道材料(42CrMo)，为采集切削过程冲击载荷及确定刀片受力区域形状和位置，首先通过切削仿真平台对该切削过程进行数值模拟，切削用量为：切削速度100 m/min，进给量0.42 mm/r，切深2 mm，工件是直径为100 mm的42CrMo棒料，刀具及工件材料物理机械性能和刀片几何角度分别如表1和表2所示.

表1刀具材料性能

Table 1Property parameters of material

材料密度/(g·cm-3)抗拉强度/MPa抗弯强度/MPa硬度泊松比弹性模量/GPa刀片13.8784.5≥118091.8HRA0.23540～600工件7.87108030HRC0.28212

表2刀具几何角度

Table 2　Geometric angle of tool　(°)

基于表3所述的理论模型，采用修正的拉格朗日算法和局部网格重划技术对该切削过程进行有限元模拟[18-19]，重点考察刀片受突变载荷情况.在该数值模拟过程中，作如下假设：①刀屑接触区的摩擦系数为恒定值；②刀屑交界面与外界环境进行均匀换热；③工件固定，刀片围绕工件轴心做旋转运动.经过计算和后处理得到如图1所示的刀片3个方向的受力情况.

表3数值模拟所依据理论模型

Table 3Main theoretical modal of numerical simulation

模型或准则模型名称表达式注释流动应力模型(本构模型)Zener-Sellars模型σ-=(ε-,ε-·,T)σ-为流动应力,ε-为等效塑性应变,ε-·为等效塑性应变率,T为绝对温度断裂准则NormalizedCockcroft&Latham准则∫ε-f0σ*σ-dε-=Cε-f为总塑性应变,σ-为等效应力,σ*为最大主应力,C为断裂阈值屈服准则VonMises准则oct=Coct为材料剪应力 刀具摩损模型Usui磨损模型w=∫apve-b/Tdtp为界面压力,v为滑移速度,T为界面温度,a、b为实验校准系数界面摩擦模型剪切摩擦模型=mk为界面摩擦剪应力,m为界面摩擦系数(此处取0.4),k为剪切屈服应力

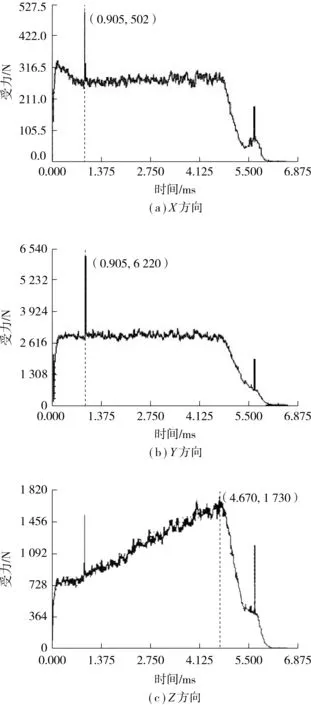
图1　刀片主切刃近域受力情况Fig.1　The load of the field near main cutting edge of tool

由图1可以看出，在数值模拟坐标系中，刀片主切刃近域受到的3个方向的力冲击载荷分别为：X方向的进给抗力Ff为502 N，Y方向的主切削力Fc为6 220 N，Z方向的切深抗力Fp为1 730 N，将这3个冲击载荷作为接下来刀具主切刃近域微观破损分析的输入载荷，用数值求解方法来分析该硬质合金刀片在这3个方向的冲击力作用于其前刀面主切刃近域情况下的微观破损情况.

2.2硬质合金刀片PD模型的构建与求解

(6)

(7)

式中，n表示时间步序号，Vm表示质点xm在m处的体积.令Δ表示一个立方晶格体积常数，由于参考域被均匀离散，所以有：

Vm=Δ3

(8)

(9)

(10)

根据该硬质合金刀片切削42CrMo的数值仿真分析结果，对该刀片主切刃近域施加载荷如图2(a)所示，其受力区域如图2(b)所示.综合考虑切削用量(进给量和切深)，载荷施加位置近似为前刀面主切刃附近长方形区域.

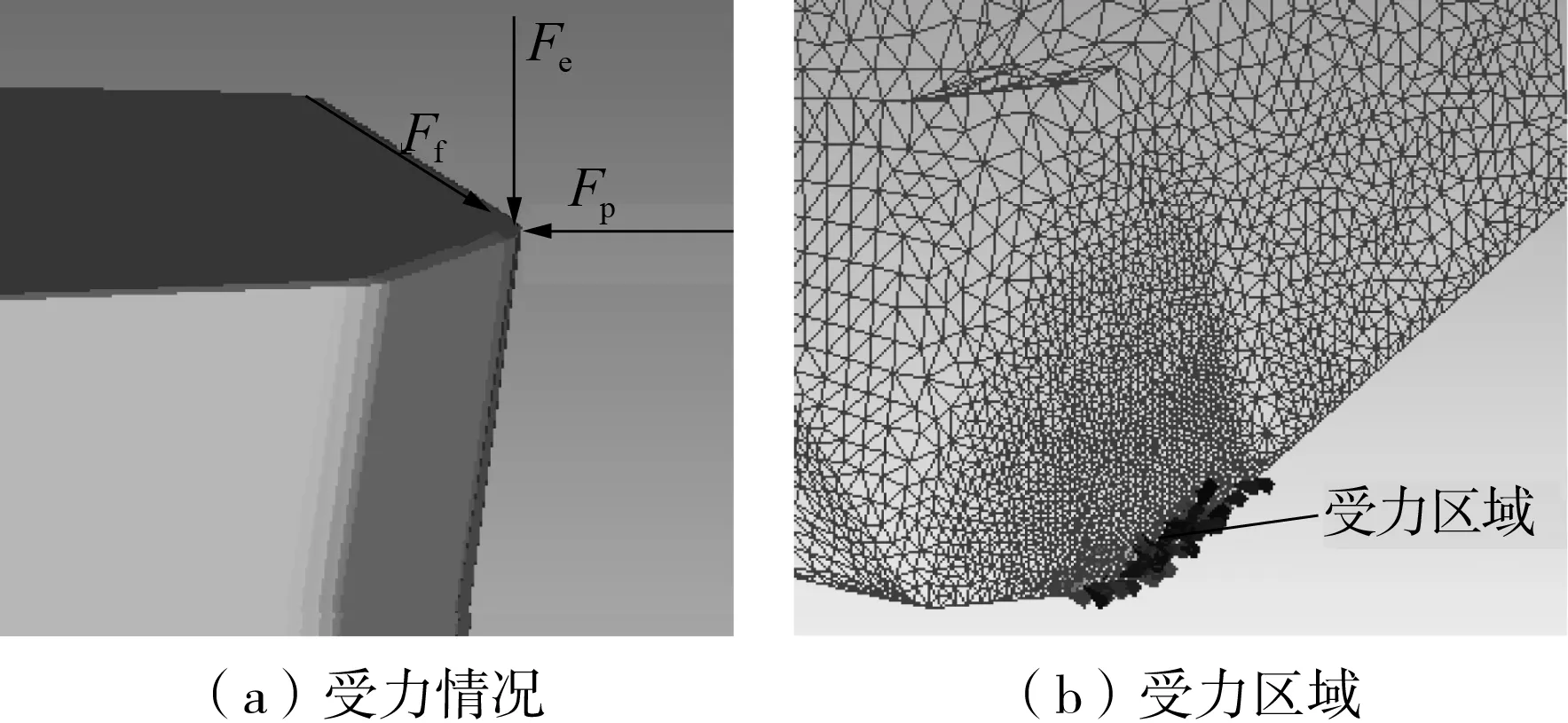
图2　刀片主切刃近域施加载荷情况Fig.2　Loading situation of the field near main cutting edge of tool

立方体晶格体积常数Δ取为0.5 mm，则Vm=1.25×10-10m3，参考域半径δ取为3Δ即1.5 mm，极限伸长率取为0.005，时间步长dt取为1 μs.建立PD模型示意如图3所示.

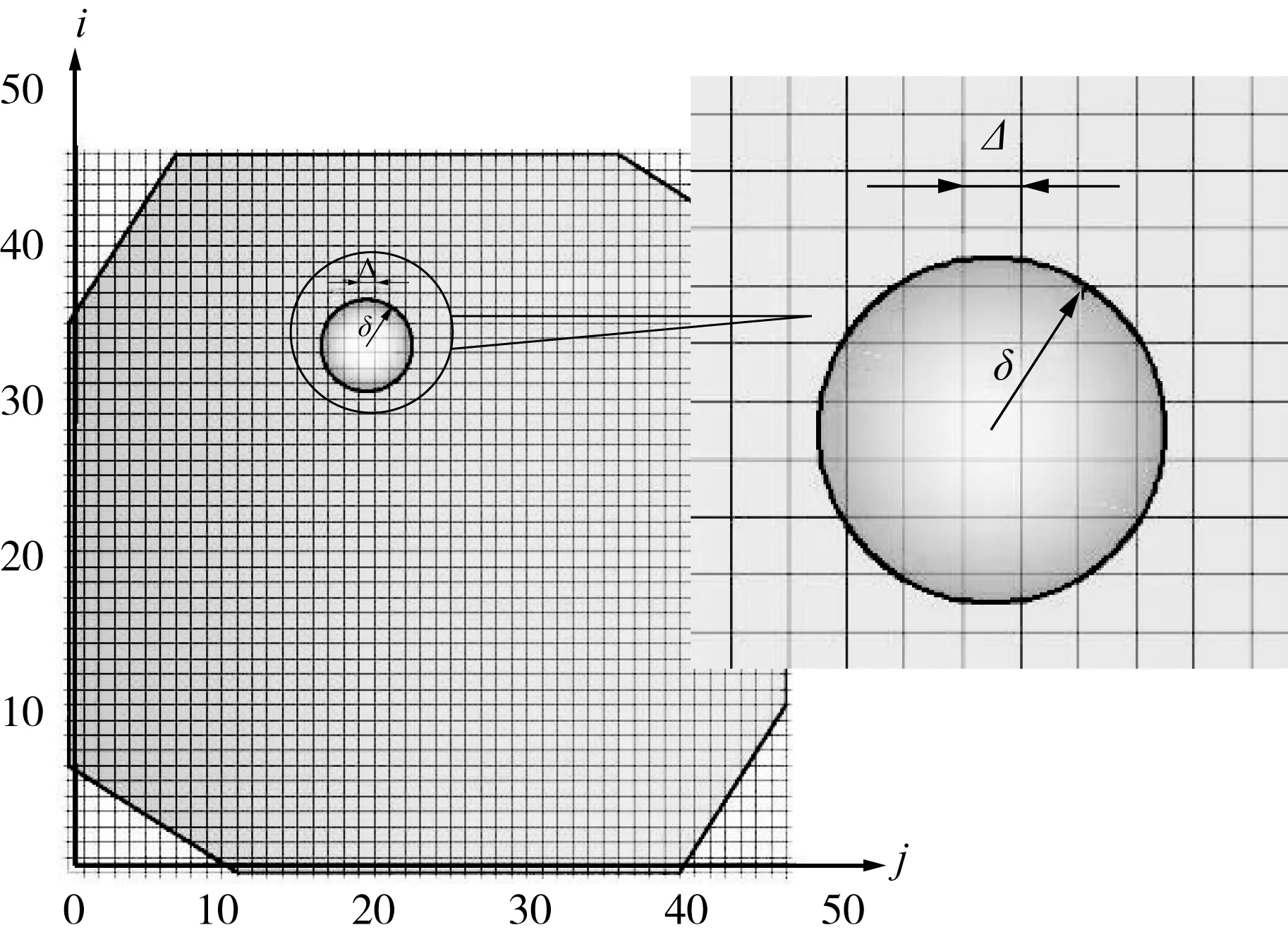
图3　刀片PD模型示意图Fig.3　Schematic diagram of PD model of cutting tool

根据上述的PD数值模拟方法，在Visual Studio环境下采用C语言编写刀片PD建模和分析程序，C程序编写流程如图4所示.经过5 000个时间步计算，且在时间步为1 000、2 000、3 000、4 000和5 000时分别输出结果，即记录下刀片主切刃近域在3个相互垂直方向上载荷作用下的微观破损情况.

2.3PD分析数据图形化处理

经过编程计算，在Visual Studio环境下计算生成结果均为txt.格式的文本，包含的是整个求解过程中计算域内所有质点的三维坐标，无法直观进行刀片破损分析，需要结合Matlab图形处理单元将求解结果可视化.在Matlab中调用数据可视模块里的数值绘图指令[24]进行离散点的可视化，通过测量刀片主切刃近域材料质点的位移量，来间接反应刀片该区域的破损情况.

3车刀片主切刃近域微观破损分析

在本研究中，分别从刀片主切刃近域的X-Y和X-Z视图(Matlab坐标系中)，重点分析刀片在切深抗力、主切削力、进给抗力综合作用下，其材料质点间“键”的断裂带来的质点位移情况.经过 5 000步计算后，根据Matlab测量工具测出待测点的三维坐标，在Z方向即6 220 N主切削力的作用方向，刀片刀尖区域材料质点最大位移量约为1.363 mm.同样，在Y方向即1 730 N切深抗力的作用方向，刀片刀尖处材料质点最大位移量约为 0.193 mm.

材料质点由于受到外载荷的作用而产生位移，质点间“键”开始变形，或压缩或伸长；当处于伸长状态的“键”的伸长率大于该材料极限伸长率s0时，则该“键”断裂，该处材料质点则更易发生相对大位移[25].本研究中，刀片主切刃近域材料微裂纹的产生和扩展过程是间接通过该区域材料质点的位移来衡量的.在整个计算过程中，重点对X-Y、X-Z视图里Y方向(切深方向)和Z方向(主切削方向)的最大位移量进行研究，每隔1 000步记录一次数据.同时为便于对比该硬质合金刀片在主切刃近域材料在不同方向的位移情况，将两组数据进行整合处理，得出如图5所示的Y向和Z向最大位移的对比曲线.由图可知，Z方向最大位移量比Y方向大，随着时间步的积累这种差异越明显.由此说明该硬质合金刀片在3个方向载荷的综合作用下其主切刃近域材料的破损主要是由材料质点在主切削方向的位移引起的.

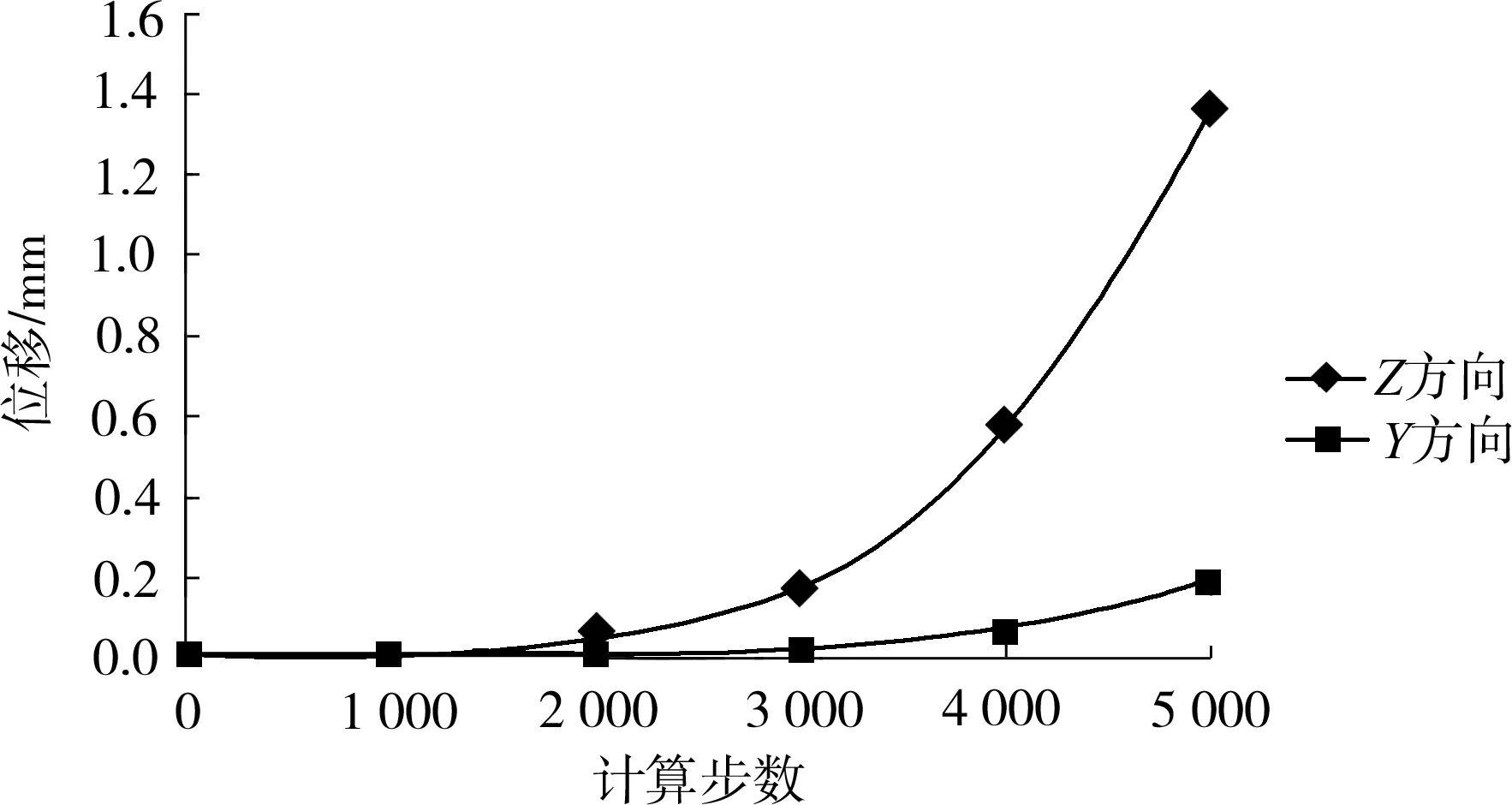
图5　不同方向位移程度对比Fig.5　Comparison of deformation extent in different directions

图6呈现了刀片主切刃近域材料的微观裂纹萌生和扩展过程.图6(a)和6(b)所示的刀尖放大视图展现了微裂纹的初期萌生和亚稳扩展情况；由图6(c)可以看出，主切刃近域小部分材料质点由于“键”的断裂产生大位移，同时裂纹在逐渐生长扩大，即处于失稳扩展阶段，随着时间推移，最终此处出现较明显的破损.

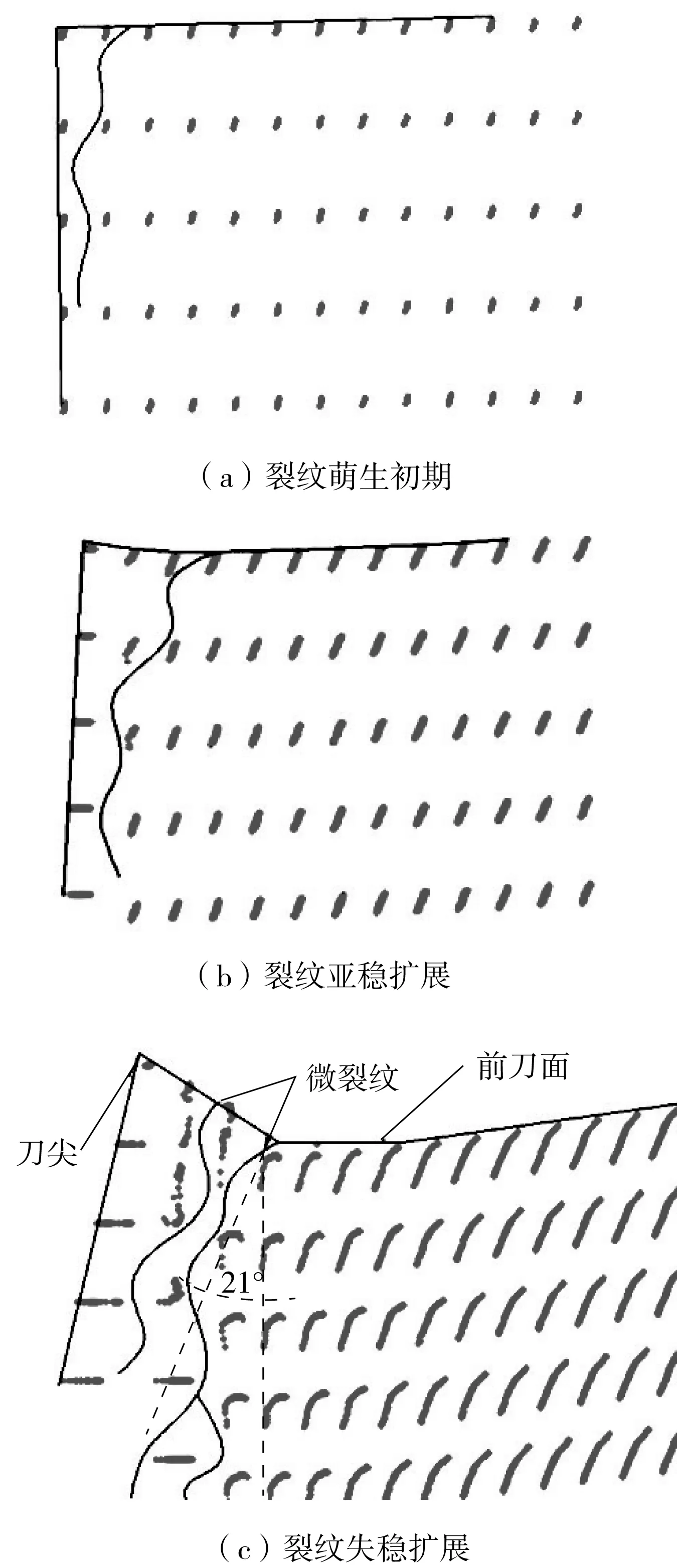
图6　主切刃近域裂纹扩展过程Fig.6　Crack growth process of the field near main cutting edge

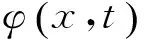
4切削试验研究

根据仿真试验情况，通过搭建合理的切削试验平台，将该硬质合金车刀片C/26417-XMLS进行相同切削条件的切削试验，即切削用量分别为：切削速度100m/min，进给量0.42mm/r，切深为2mm.采用粗车42CrMo棒料，试验机床型号为JILING-CW6163C，断续切削40min，现场切削情况如图7所示.

图7　切削试验现场Fig.7　Scene of cutting test

试验结束后，采用Olympus金相显微镜和GEmini扫描电镜对断续切削过刀片的主切刃近域进行微观破损情况观测，经过调整图像放大倍数，刀片相同区域观测结果如图8所示.图8(a)为金相显微镜放大200倍所采集的后刀面微裂纹图像，图8(b)为扫描电镜放大150倍所采集的后刀面微裂纹图像.

图8　后刀面微观形貌Fig.8　Microstructure of major flank

由图8(a)、8(b)可看出，浅色区域为切削过程产生的划痕，两图中裂纹辅助线为近似垂直于前刀面向内的微裂纹，呈现形态与PD数值分析方法模拟结果有一定的相似性，微裂纹与前刀面法向夹角均在18°～25°范围内，微裂纹的产生主要是因为刀片主切刃近域受到切削系统稳定性、材料成分以及切削过程中机床振动等因素引起的冲击载荷的作用.不难预测随着切削时间的推移，这种非连续微裂纹会不断累积，最终造成刀片的破损.

5结语

研究结果表明，基于近场动力学理论硬质合金刀具微观破损数值模拟方法能够相对客观地呈现刀片近主切刃区域材料微观破损的产生与扩展过程：该工况(切削速度100 m/min，进给量0.42 mm/r，切深2 mm)下的刀片微观破损主要是由切削过程中机床振动、工件材料内部夹杂物及试验平台稳定性等不确定因素所产生的冲击载荷引起的与前刀面法向呈约20°夹角的微裂纹导致，且该裂纹有向里层材料非连续扩展的趋势.通过切削试验结果可看出，该数值分析方法在一定程度上能够有效预测刀具主切刃近域非连续微观破损情况，尤其是裂纹萌生位置和扩展方向，为刀具切削过程中的离散破损预测提供了一种理论方法.但是作为一种新兴的数值模拟方法，PD理论在刀具破损分析上的应用仍存在问题：

首先，该基于PD理论刀具微观破损数值分析方法的分析精度一定程度上依赖于外界设定的载荷施加区域的形状和位置，该数值分析方法本身建立在微观环境下，所以载荷施加区域的形状和位置的轻微变动将可能带来分析结果的明显差异.

其次，该数值分析方法所建立的一个断裂判断条件是基于刀具材料极限伸长率，极限伸长率不同的取值会引起材料质点不同的位移情况，破损的产生时刻和扩展情况也会发生相应的变化.

最后，在研究对象的PD模型建立上，主要针对形状规则且简单的几何模型，对于结构复杂模型(如车刀模型)的建立将可能成为今后研究的重点内容之一.

参考文献：

[1]杨明伦，邵华.基于EEMD和IMF能量分布的刀具破损识别 [J].组合机床与自动化加工技术,2013(4):54-58.

YANG Ming-lun,SHAO Hua. Identification of AE signal for tool breakage monitoring based on EFMD [J].Modular Machine Tool & Automatic Manufacturing Technique,2013(4):54-58.

[2]贺晓辉，鄢萍，张佳毅，等.功率信息互相关法的刀具破损在线监测 [J].重庆大学学报(自然科学版),2011,34(9):9-16.

HE Xiao-hui,YAN Ping,Zhang Jia-yi,et al. On-line tool breakage monitoring method based on power information and cross-correlation algorithm [J]. Journal of Chongqing University(Natural Science Edition),2011,34(9):9-16.

[3]沈峰，章青，黄丹，等.冲击载荷作用下混凝土结构破坏过程的近场动力学模拟 [J].工程力学,2012,29(1):12-15.

SHEN Feng,ZHANG Qing,HUANG Dan,et al. Peridynamics modeling of failure process of concrete structure subjected to impact loading [J].Engineering Mecha-nics,2012,29(1):12-15.

[4]胡祎乐，余音，汪海.基于近场动力学理论的层压板损伤分析方法 [J].力学学报,2013,45(4):624-628.

HU Yi-le,YU Yin,WANG Hai. Damage analysis method for laminates based on peridynamic theory [J]. Chinese Journal of Theoretical and Applied Mechanics,2013,45(4):624-628.

[5]WECKNER Olaf,ASKARI Abe,XU Jifeng. Damage and failure analysis based on Peridynamics-Theory and applications [C]∥Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference. Hawaii:AIAA,2007:7440-7449.

[6]YU K,XIN X J,LEASE K B. A new adaptive integration method for the peridynamic theory [J].Modelling Simulation in Materials Science and Engineering,2011,19(4):1-24.

[7]WECKNER Olaf,EMMRICH Etienne.Numerical simulation of the dynamics of a nonlocal inhomogeneous infinite bar [J].Journal of Computational and Applied Mecha-nics,2005,6(2):311-319.

[8]GHAJARI M,IANNUCCI L,CURTIS P. A peridynamic material model for the analysis of dynamic crack propagation in orthotropic media [J].Computer Methods in Applied Mechanics and Engineering,2014,276:431- 452.

[9]HUANG Dan,ZHANG Qing,QIAO Pizhong. Damage and progressive failure of concrete structures using non-local peridynamic modeling [J].Science China Technological Sciences,2011,54(3):591-596.

[10]SILLING S A. Reformulation of elasticity theory for discontinuities and long-range forces [J]. Journal of the Mechanics and Physics of Solids,2000,48(1):175-209.

[11]ERKAN Oterkus. Peridynamic theory modeling three-dimensional damage growth in metallic and composite structures [D].Tucson:University of Arizona,2010.

[12]HUANG Dan,LU Guangda,QIAO Pizhong. An improved peridynamic approach for quasi-static elastic deformation and brittle fracture analysis [J].International Journal of Mechanical Sciences,2015,94(5):111-122.[13]GU Xian-Ming,HUANG Ting-Zhu,ZHAO Xi-Le. Circulant preconditioned iterative methods for peridynamic model simulation [J].Applied Mathematics and Computation,2014,248(12):470- 479.

[14]OTERKUS Erkan,MADENCI Erdogan,WECKNER Olaf.Combined finite element and peridynamic analyses for predicting failure in a stiffened composite curved panel with a central slot [J].Composite Structures,2012,94(3):839-850.

[15]CHEN Zi-guang,BOBARU Florin. Peridynamic modeling of pitting corrosion damage [J]. Journal of the Mechanics and Physics of Solids,2015,78(5):352-381.

[16]ERBAY H A,ERKIP A,MUSLU G M. The Cauchy problem for a one-dimensional nonlinear elastic peridynamic model [J]. Journal of Differential Equations,2012,252(8):4392-4409.

[17]STEVEN F Henke,SACHIN Shanbhag. Mesh sensitivity in peridynamic simulations [J]. Computer Physics Communications,2014,185(1):181-193.

[18]WENKE Hu,YOUN Doh Ha,FLORIN Bobaru. Peridynamic model for dynamic fracture in unidirectional fiber-reinforced composites [J]. Computer Methods in Applied Mechanics and Engineeing,2012,217(4):247-261.

[19]HU Yi-le,YU Yin,WANG Hai. Peridynamic analytical method for progressive damage in notched composite laminates [J]. Composite Structure,2014,108(1):801-810.

[20]AMIT Katiyar,JOHN T Foster,HISANAO Ouchi. A peri-dynamic formulation of pressure driven convective fluid transport in porous media [J]. Journal of Computational Physics,2014,261:209-229.

[21]RAMI Jabakhanji,RABI H Mohtar. A peridynamic mo-del of flow in porous media [J]. Advances in Water Resources,2015,78(4):22-35.

[22]JAMES O’Grady,JOHN Foster. Peridynamic plates and flat shells:A non-ordinary,state-based model [J]. International Journal of Solid and Structure,2014,51(25):4572-4579.

[23]SELDA Oterkus,ERDOGAN Madenci,ERKAN Oterkus,et al. Hygro-thermo-mechanical analysis and failure prediction in electronic packages by using peridynamics [C]∥Proceedings of the 64th Electronic Components and Technology Conference. Orlando:ECTC,2014:973-982.

[24]JAMES O’Grady,JOHN Foster. Peridynamic beams:a non-ordinary,state-based mode [J]. International Journal of Solid and Structure,2014,51(18):3177-3183.

[25]BUCHKREMER S,KLOCK F,LUNG D. Finite-element-analysis of the relationship between chip geometry and stress triaxiality distribution in the chip breakage location of metal cutting operations [J]. Simulation Modelling Practice and Theory,2015,55(6):10-26.

Key words: peridaynamics; cemented carbide tool; micro breakage; numerical analysis; prediction

Key words:burnishing; titanium alloys; fretting wear

Peridynamic Theory-Based Prediction of Micro Breakage of Cemented Carbide Tool

JIANGHong-wan1HELin1,2FANLin1ZHAOXian-feng1ZHANGang1

(1.College of Mechanical Engineering,Guizhou University,Guiyang 550025,Guizhou,China;2.Guizhou Normal College,Guiyang 550018,Guizhou,China)

Abstract:Breakage is one of the important forms of tool failure.The traditional tool breakage analysis is mostly carried out through cutting test,which not only costs a lot but also lasts a long cycle.On the basis of peridynamic (PD) theory,this paper focuses on the micro breakage in the field near the main cutting edge in cutting process of 42CrMo large-diameter oil pipeline with cemented carbide tool.Firstly,finite element simulation of the cutting process is carried out to extract tool load.Secondly,in Visual Studio environment,the program for PD modeling and analysis is compiled by using C language according to PD theory.Then,with the help of image processing unit in Matlab,numerical analysis of micro breakage in the field near the main cutting edge of the cemented carbide tool is made in terms of the crack initiation position,the displacement trend of material particle in different directions and the growth trend of crack.The results show that the PD theory-based numerical analysis of cemented carbide tool’s micro breakage helps reveal the mechanism and growth of micro breakage of the tool material in the field near the main cutting edge,that is,the micro breakage under certain working conditions is mainly caused by the shock load-induced micro cracks which is in a certain angle with the normal of rake face,and that the breakage trends to spread to the internal material discontinuously.

收稿日期：2015- 08- 04

*基金项目：国家自然科学基金资助项目(51265005)

Foundation item:Supported by the National Nataral Science Foundation of China(51265005)

作者简介：蒋宏婉(1988-)，女，博士生，主要从事刀具创新设计和分子动力学研究.E-mail: jhw.969@163.com † 通信作者： 何林(1965-)，男，教授，博士生导师，主要从事刀具创新设计、摩擦与表面工程研究. E-mail:helin6568@163.com

中图分类号：TG712

doi:10.3969/j.issn.1000-565X.2016.03.002