平板型铝合金格栅结构支座节点的承载性能
2016-06-17陈伟刚白光波董石麟朱忠义
陈伟刚,邓 华, 白光波, 董石麟, 朱忠义
(1. 浙江大学 空间结构研究中心,浙江 杭州 310058;2. 浙江省空间结构重点实验室,浙江 杭州 310058.3. 北京市建筑设计研究院有限公司,北京 100045)
平板型铝合金格栅结构支座节点的承载性能
陈伟刚1,2,邓华1,2, 白光波1,2, 董石麟1,2, 朱忠义3
(1. 浙江大学 空间结构研究中心,浙江 杭州 310058;2. 浙江省空间结构重点实验室,浙江 杭州 310058.3. 北京市建筑设计研究院有限公司,北京 100045)
摘要:通过有限元分析与足尺试验考察平板型铝合金格栅结构支座节点的承载性能.加载试验揭示了支座节点的位移、应变发展特点及破坏模式.有限元分析给出了支座节点中的杆件、环槽铆钉及盖板的应力分布状况.研究表明:支座节点的破坏为位于工字铝受拉翼缘的最外排铆钉孔处发生断裂;与受拉翼缘连接的下盖板存在传递路径明显的高应力区,但由于分布区域较窄并未导致盖板破坏,而上盖板的应力要低很多;受拉翼缘断裂截面处的环槽铆钉处于最不利的拉弯受力状态,但并未发生破坏;当杆件断裂时,承受的极限弯矩约为纯弯状态下强度设计值的0.9倍,剪弯比可达0.3;节点的有限元结果与试验结果吻合较好,反映了数值模拟方法的有效性.
关键词:铝合金结构;平板格栅;支座节点;断裂破坏;有限元分析
铝合金单层网格结构具有重量轻、外形美观、耐腐蚀性好、易于维护等优点[1],广泛应用于工业和民用建筑.该类结构的杆件通常采用工字型截面挤压型材(简称“工字铝”).由于焊接会显著降低铝合金母材的强度,工字铝杆件间通常采用较为可靠的机械连接形式[2],其中最常用的是板式节点.板式节点[3]是由美国Temcor公司研发的一种节点体系,具有构造简单,气动张拉环槽铆钉的施工速度快等优点.但由于该节点仅为各杆件的翼缘板相连而腹板不连,抗剪承载能力较弱,故主要应用于球面网壳等以薄膜内力为主的单层网格结构[4-5].
近年来为满足建筑设计的要求,国内一些重要工程开始将铝合金单层网壳结构应用于平板型的屋盖格栅结构中(如重庆国际博览中心、常州西太湖花博会主场馆等),并仍采用板式节点.由于平板型格栅结构以受弯为主,且铝合金材料的弹性模量较低,因此相比于以薄膜内力为主的球面网壳结构,平板型格栅结构的跨越能力和抗变形能力均较弱,一般需要设置相对较密的竖向支承点.出于构造简单、连接便利的考虑,这些支承点处支座节点的做法主要是遵循机械连接的原则通过板式节点改造而成.因支座节点对结构安全至关重要,故在进行平板型铝合金格栅结构设计时,有必要对这些以承受弯矩和剪力为主的支座节点的受力性能和承载能力进行研究.
本文结合实际工程,对平板型铝合金格栅结构的支座节点进行试验研究和有限元分析.介绍平板型铝合金格栅结构支座节点的构造及其受力特点,通过试验考察加载过程中支座节点的变形、应力发展情况和破坏模式等.采用有限元方法对试件的加载过程进行数值模拟,利用数值计算结果对模型试验的精度和有效性进行考察,并对该类型支座节点的受力特点、薄弱区域进行深入分析,提出此类平板型铝合金格栅结构支座节点的分析设计建议.
1支座节点构造及受力特点
1.1节点构造
某实际工程中平板型铝合金格栅结构是由2个正交方向杆件和一个斜向杆件构成的三向网格体系,如图1所示.格栅结构由下部撑杆支承,支承点处支座节点的具体做法是在标准板式节点的上、下盖板中心开圆孔,然后穿入一根带螺纹的实心销轴,通过拧紧上、下各2个螺母将销轴与上下盖板连接起来,在与斜向杆件垂直方向设置2个加劲撑,杆件、加劲撑与盖板之间仍采用环槽铆钉连接.根据实际需要,将销轴下端机加工成单向铰耳板或双向铰耳板与下部撑杆连接.如图2所示.

图1 平板型铝合金格栅结构Fig.1 Flat aluminum lattice structure

图2 支座节点构造Fig.2 Formation of bearing joint
1.2受力特点
与以承受薄膜内力为主的单层球面网壳不同,平板型铝合金格栅结构的节点在跨中以承受正弯矩为主,在支座处同时承受负弯矩和较大剪力(支座反力),如图3所示.

图3 竖向荷载下平板型格栅结构的弯矩分布示意图Fig.3 Illustrative moment distribution of flat aluminum lattice structure under vertical loads
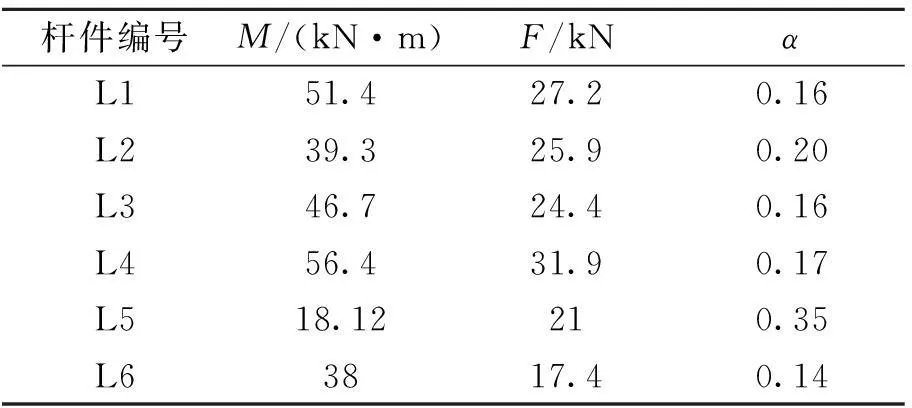
针对该平板型铝合金格栅结构实际工程,由设计单位根据整体结构分析结果,提供了代表性支座节点的6根相连杆件的最不利内力设计值,作为确定节点试验加载量的参考值,如表1所示.表中,杆件剪力F与弯矩M间的相对大小通过剪弯比α=FH/M来描述,其中杆件截面高度H=300 mm.从式中可知,α值越大,说明剪力也越大,反之则剪力越小.
表1 杆件最不利内力设计值
Tab.1Design values of the most unfavorable internal forces in members
杆件编号M/(kN·m)F/kNαL151.427.20.16L239.325.90.20L346.724.40.16L456.431.90.17L518.12210.35L63817.40.14
从表1可以看出,支座节点处的4根正交杆件(L1~L4)承受较大的弯矩,2根斜向杆件(L5、L6)的弯矩相对较小.节点域6根杆件的剪力设计值相差不大,剪弯比最大为0.35,最小为0.14.
2试验设计
2.1试件和加载装置
选取该实际工程中的足尺支座节点作为试件进行静力加载试验,如图4所示.试件中的杆件、加劲撑和圆形盖板均采用国产6061-T6铝材,杆件截面规格和盖板尺寸如表2所示.销轴和螺母为Q345-B钢材,销轴直径为100 mm.环槽铆钉材质为304HC不锈钢,直径为9.66 mm,孔径为9.96 mm.杆件尺寸及编号如图5所示,F1~F6为杆件L1~L6各加载点对应的载荷值,杆件L1~L4的加载点位置相同:杆件L5~L6的加载点位置相同,试件基本参数均列于表2.
为满足该类节点试件的加载要求,专门设计了节点试验加载架,如图6所示.该加载架采用Q345钢,主要由立柱、顶部连梁(包括交叉连梁和边连梁)、杆端辅助短柱及中心辅助短柱4部分组成.在立柱上距地面700 mm处设牛腿,牛腿顶面标高与杆端辅助短柱顶面标高一致.中心辅助短柱为空腔型,腔内放置液压千斤顶.节点销轴下端加工成半球状,与腔内千斤顶上设置的凹槽形垫块相配合,以保证千斤顶顶紧时节点可转动.4根立柱柱脚及2根杆端辅助短柱底部通过锚栓固定在试验室的地槽上.正交杆件L1~L4外端搁置于4根立柱的牛腿上,斜向杆件L5、L6外端放置于2个辅助短柱上.在距牛腿顶面280 mm高处设置侧向限位角钢,防止L1~L4在加载过程发生端截面的扭转.利用连梁下方设置的6个300 kN液压千斤顶实现加载,千斤顶采用吊架固定在连梁上,各加载点处均放置刚性垫块,以保证该处杆件能均匀受力.

图4 支座节点试验试件Fig.4 Experimental specimen

节点构件规格/mm数量材料L1~L4H300×150×8×1046061-T6L5、L6H300×150×6×1026061-T6盖板Φ450×1026061-T6销轴M1001Q345-B环槽铆钉M9.66160304HC

图5 杆件编号及加载点位置Fig.5 Member numbering and loading points

图6 加载架和试验装置Fig.6 Loading frame and test equipments
2.2内力模拟
根据支座节点的连接构造形式及设计单位提供的支座节点内力值可以看出,该连接近似刚接.同时,为确定试验加载方案,假定节点为刚性连接,观察外力作用下与节点相连各杆件杆端的内力分配情况.如图7所示为试件的简化计算模型.
6根杆件在板式支座节点中心处定义为刚接连接,杆件外端节点施加铰接约束,而中心节点仅施加一个竖向位移约束.在加载点位置对正交杆件L1~L4施加单位荷载,斜向杆件L5~L6施加0.5倍单位荷载.如表3所示为不同约束条件下的杆件内力,表中A、B分别指考虑中心节点约束和撤去中心节点约束.从表3中可以看出,当施加中心节点约束时,节点域各杆件剪力在外荷载作用下的增长速度远大于其弯矩值;L1~L4杆件截面的剪弯比α为1.01,L5、L6杆端截面的剪弯比为0.63,和实际工程内力相差较大.

图7 试件简化计算模型Fig.7 Simplified analytical model of specimen

杆件编号AM/(kN·m)F/kNαBM/(kN·m)F/kNαL1~L40.220.741.010.650.080.04L5~L60.100.210.630.500.160.10
为使杆件截面承受较大的弯矩,撤去中心节点竖向约束,从表3中可以看出,此时杆件截面弯矩明显提高,但杆件截面剪力和剪弯比却又相对较小.经综合分析,最终决定采用两阶段加载法来模拟节点同时产生较大弯矩和剪力的情况.第1阶段加载时先撤去中心节点的竖向约束,这样可使杆件在节点域产生较大的杆端弯矩.当弯矩达到一定量值时,施加中心节点竖向约束并进入第2阶段加载.该阶段杆件截面弯矩增长有限,而杆件截面剪力增长迅速.
2.3加载方案
由我国现行《铝合金结构设计规范》[6]可知6061-T6铝材的设计强度为210 MPa,由此可计算试件中工字铝杆件在纯弯状态下的强度设计值为M0=108.78 kN·m.观察表1,发现实际工程支座节点中最大的杆件截面弯矩为56.40 kN·m,约为0.5M0.
为满足本工程设计的要求并有效考察该类节点的受力性能和极限承载能力,综合分析后确定试验中第一加载阶段正交杆件上加载点的最大加载值F1~F4取150 kN,斜向杆件上加载点加载值F5~F6取75 kN.由表3可知,此时对应的杆件截面弯矩分别为116和97 kN·m.为便于表述,定义此组加载值为F0.
试验时采用6个加载点分级同步加载.加载初期每级荷载增量为F0/4.当加载值超过3F0/4后,每级荷载增量减少为F0/8.加载至F0(即第1阶段加载结束)后,顶升中心千斤顶开始第2阶段加载.此间进一步将每级加载值减小至F0/12,直至试件发生破坏.
2.4测点布置
在下盖板的销轴边缘布置2个位移计D1、D2测量试件的竖向位移,如图8所示.同时,对杆件、盖板进行应变测量.应变测点位置如图9所示,分别为:

图8 位移测点Fig.8 Displacement gauging points
1) 盖板边缘附近的工字铝上、下翼缘各布置正应变测点2个(所在截面称为测点截面),主要测量该截面上的测点正应力,并计算出杆件截面弯矩.
2) 杆件测点截面中性轴处的腹板2面对称布置应变花,主要用于测量剪应变并计算该截面的剪力.
3)上、下盖板表面对应各杆件分别布置应变测点6个.
翼缘和腹板上测点编号分别为Sx-i和Wx-i,其中x为杆件编号,i为应变片编号,如图9(b).盖板测点编号为PU(D)-i,其中U和D分别为上、下盖板,见图9(d).

图9 应变测点Fig.9 Strain gauging points
3试验结果和分析
3.1试验现象
由《铝合金结构设计规范》[6]可知,铝合金材料的弹性模量为70×103MPa,因此易知T6061-T6型材设计强度对应的应变值为3.0×10-3.邓华等[1]进一步对6061-T6铝材进行拉伸试验,确定该材料σ0.2对应的屈服应变参考值为3.5×10-3.对该试件进行第1阶段加载的过程中,铝合金杆件和节点域并未出现明显的变形和破坏现象,且各测点应变值均小于屈服应变,表明试件总体上处于弹性受力状态.
顶升中心辅助短柱空腔内的千斤顶直至与销轴下端半球面贴紧,并开始第2阶段加载.当加载至约1.2F0时,突然听到“嘭”的响声,杆件L1在节点域内的下翼缘沿前排铆钉孔截面发生断裂如图10(a)所示,而后沿腹板发生45°左右的斜向断裂如图10(b)所示.相应地F1加载点的千斤顶压力迅速下降,且无法继续加载,试验终止.

图10 杆件L1断裂破坏Fig.10 Failure with fracture of member L1
3.2荷载-位移曲线

图11 测点D2荷载-位移曲线Fig.11 Load-deformation curves of gauging point D2
如图11所示为位移测点D2的荷载-位移曲线,图中,Δ为位移;Fn为相对荷载值,Fn=当前荷载/F0.由于第2阶段加载时中心千斤顶已顶升,故该阶段测点D2的位移基本不再发生改变. 从图11中可以看出,第1阶段的荷载与位移呈明显的线性关系,也说明试件总体处于弹性受力状态.
3.3荷载-应变曲线
1) 盖板测点

图12 下盖板测点荷载-应变曲线Fig.12 Load-strain curves of lower cover plate
以下盖板表面应变测点的荷载-应变ε曲线为对象进行分析,如图12所示.从图12中可以看出,各测点在外荷载作用下的变化趋势基本一致.加载前期,各测点均在弹性范围内,且应变曲线保持线性关系.然而,加载到约0.7F0时,多个测点开始表现出非线性特征,其中PD-3、PD-4尤为明显.第1阶段加载结束时,这2个测点的应变值实际上已超过屈服应变值,并随荷载的增加进一步快速增大.其余测点的应变值在整个受力过程中均小于铝合金的屈服应变.相比之下,上盖板各测点在加载过程中处于受压状态,但应变最大值仅为1.3×10-3,相比下盖板要小很多.
2. 杆件测点
根据试件的对称性,仅对L1、L4、L6这3根杆件翼缘测点应变进行分析.如图13所示为3根杆件翼缘测点的荷载-应变曲线.从图13中可以看出,同根杆件上对称测点的荷载-应变曲线基本接近,且上翼缘测点受压,下翼缘测点受拉.仅测点SL4-1和SL4-2可能受测量误差的影响存在一定的差异.在第1阶段加载过程中,各测点应变曲线基本保持线性关系;进入第2加载阶段后,各测点的应变值虽有所增加,但除测点SL1-3、SL4-4外均小于屈服应变值(图13中虚线对应位置).

图13 杆件翼缘测点荷载-应变曲线Fig.13 Load-strain curves of gauging points on member’s flanges
3.4杆件测点截面内力
根据杆件同一测点截面上、下翼缘的4个测点正应变值,由材料力学[7]公式可换算成该截面的弯矩.同理,根据中性轴处的测点剪应变值,也可计算出该截面的剪力.具体计算公式如下:

(1)

(2)
式中:σi为同一测点截面上、下翼缘测点的正应力绝对值,i=1,2,3,4;τj为测点截面中性轴处剪应力,j=1,2;Iz为工字铝截面惯性矩;Sz为对工字铝截面中性轴的静矩;y为测点距截面中性轴距离;tw为工字铝截面腹板厚度.
在各级荷载作用下,杆件L1、L4、L6测点截面弯矩和剪力的变化分别如图14和15所示.从图14中可以看出,第1加载阶段杆件截面弯矩增长速度较快.进行第2阶段加载后,弯矩较大杆件L1、L4的测点截面弯矩增速明显放缓,增量非常有限.杆件L1的荷载-弯矩曲线在最后阶段快速减小,这主要是由于该杆发生断裂使得截面内力迅速释放.由图15可知,杆件测点截面的荷载-剪力关系与弯矩变化正好相反.第1加载阶段,剪力只是缓慢增加.当中心节点竖向位移约束后,测点截面剪力随荷载的增加而快速增加.如表4所示为在试件发生破坏前一级荷载作用下(该级加载下杆件截面弯矩达到最大),各杆测点截面的弯矩、剪力及由试验值计算得到的剪弯比α,表中β1、β2分别为弯矩和剪力试验值与表1内力设计值的比值.δ1、δ2为误差,分别为弯矩和剪力的试验值减去有限元值除于试验值.从表4中可以看出,发生断裂的杆件L1能承受的最大弯矩约为表1中设计值的1.86倍,纯弯状态下强度设计值的0.9倍.杆件承受的最大剪力约为设计值的3.56倍,剪弯比为0.30.
4有限元分析模型
4.1试件材料参数及本构关系
支座节点的数值模拟涉及到铝合金型材和盖板、不锈钢铆钉3种材料.在一般情况下,不锈钢和铝合金材料的应力-应变(σ-ε)呈非线性关系,且2种材料的应力-应变关系均可采用Ramberg-Osgood模型[8]来描述,即

(3)
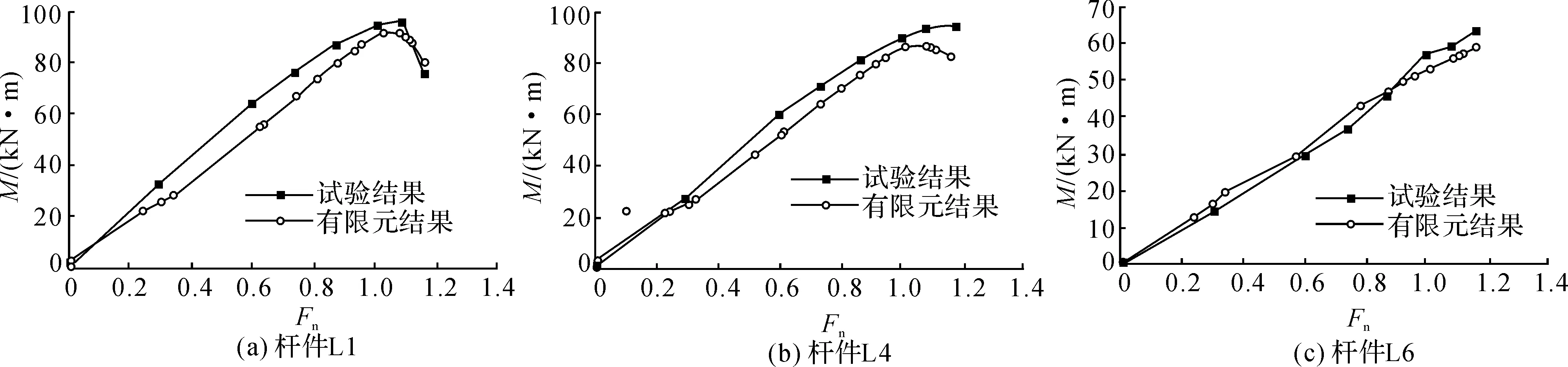
图14 测点截面的荷载-弯矩曲线Fig. 14 Load-bending moment curves of measuring sections

图15 测点截面的荷载-剪力曲线Fig. 15 Load-shearing force curves of measuring sections
式中:n为反映材料应力-应变关系非线性程度的系数,称为应变硬化系数;σ0.2为残余应变为0.2%时对应的应力;E为初始弹性模量.
对于铝合金材料,一般根据Steinhardt的建议[9]取n=σ0.2/10,其中σ0.2单位为MPa.对于不锈钢材料,通常采用修正的Ramberg-Osgood模型[10]:
(4)
式中:n=ln20/ln(σ0.2/σ0.01);m=1+3.5σ0.2/σu,为应力大于σ0.2时的材料应变硬化系数;σu为极限应力;εu=1-σ0.2/σu为对应σu的拟合应变; E0.2=E/(1+0.002nE/σ0.2),为残余应变为0.2%时对应的弹性模量,σ0.01为残余应变为0.01%时对应的应力.邓华等[1]根据材性测试结果,分别计算出6061-T6铝合金和304HC不锈钢2种材料的主要物理和力学参数,如表5所示.表中ν为泊松比.
表52种材料的力学参数和应变硬化系数
Tab.5Mechanical parameters and strain hardening coefficients of two materials

牌号σ0.01/MPaσ0.2/MPaσu/MPaE/GPanmν6061-T6—246.6283.469.824.7—0.3304HC290.1460.7724.21896.483.230.3
4.2模型建立
根据文献[11]中所确立的铝合金板件环槽铆钉连接有限元模型建立方法,在ABAQUS中采用八节点六面体非协调模式单元(C3D8I)模拟节点试件的工字铝杆件、盖板、加劲撑及环槽铆钉如图16所示.与铝合金板件相比,中心钢销轴具有较大的刚度.为便于分析,建立有限元模型时不再对钢销轴按实体元建模,而是将上、下盖板上销轴孔边周圈节点的三向线位移一并耦合,即模拟上、下盖板在刚性销轴约束下的协同变形情况.6根杆件的加载点位置与试验相同,采用和试验相同的方式进行加载.

图16 试件有限元模型Fig.16 Finite element model of specimen
在支座节点有限元模型中,通过建立8个接触对来考虑环槽铆钉与铝合金板件(盖板、杆件翼缘)间、盖板与杆件翼缘间的接触摩擦以及铆钉杆和孔壁之间的挤压作用,接触对定义及其示意分别如表6和图17所示.根据接触界面介质不同将各接触对的摩擦系数分为2组,即铝合金材料之间的摩擦系数μ1和不锈钢与铝合金材料间的摩擦系数μ2. 在有限元模型中分别取2组摩擦系数为μ1=0.15、μ2=0.25.在ABAQUS中利用BoltLoad命令将预紧力分为多个分析步逐步施加.根据邓华等[1]的实测结果,取环槽铆钉的预紧力F=18 kN.

表6 接触对定义

图17 板式节点接触面Fig.17 Contact interfaces of lap connection
5有限元结果的对比与分析
5.1杆件测点截面内力
为更直观对比有限元计算结果与试验结果的异同,将有限元分析得到的各杆件截面的荷载-弯矩曲线、荷载-剪力曲线一并列于图14和图15.从这2个对比图可以看出,有限元计算结果与试验结果总体吻合较好.对具体数值进行对比(详见表4)发现,除杆件L4截面剪力存在18.44%的较大误差外,其余杆件截面内力的误差均在10%左右.但应该指出,以上误差的产生除试验中试件加工误差、构件安装误差、加载偏心、测量误差等因素外,实际上由于有限元分析中也存在接触、摩擦、塑性变形等较为复杂的非线性因素,在迭代和收敛过程中也存在一定的数值计算误差.
5.2变形及应变比较
1)试件变形
将通过有限元分析得到的测点D2的荷载-位移曲线一并列于图11,发现其与试验曲线吻合很好.但有限元计算得到的荷载-位移曲线在加载初期有一段斜率较小的波动(交叉)段,这主要是由于盖板与杆件上、下翼缘接触面产生相对滑移所引起的.
2)测点应变
重点关注受力较大的下盖板和工字翼缘,将有限元分析得到的部分测点的荷载-应变曲线与试验结果如图18所示.从图18中可以看出,试验结果和有限元计算结果均能较好地吻合,部分测点的应变数值虽在一定程度上受测量误差的影响,但差异总体上较小.
5.3破坏形态分析
重点关注杆件L1在杆端下翼缘与盖板连接区域的Mises应力情况,如图19所示.从图19中可以看出,其最大Mises应力为310.47 MPa,约为铝合金材料屈服强度246 MPa的1.3倍,且主要集中在前排铆钉孔附近的位置,并向后排逐渐递减,这与加载过程中该位置率先发生破坏(图10)是一致的.
5.4环槽铆钉受力
如图20所示为连接杆件L1下翼缘与盖板的环槽铆钉Mises应力云图.从图20中可以看出,同图19中该位置的铆钉孔受力情况相对应,位于前排的环槽铆钉受力最大,并向后排逐渐递减,其最大Mises应力为496.28 MPa,略大于304HC不锈钢材料屈服强度460 MPa.此外,从图20中还可以看出,受节点试件承受弯矩和剪力的影响,环槽铆钉处于拉弯受力状态.
5.5盖板应力
2块盖板在加载完成后的Mises应力云图如图21所示.从图21(a)中可以看出,下盖板局部区域达到屈服应力,主要集中在斜杆L5、L6相对应的销轴孔边及L1~L4铆钉孔连线截面处(图中黑色箭头线),且这些应力较大区域也形成明显的应力传递路径,将内力经销轴传至下部支撑.除以上区域外,下盖板其他区域应力均小于设计强度210 MPa,处于弹性范围内.上盖板图21(b)除斜杆对应的销轴孔区域及铆钉孔存在一定的应力集中外,整体的应力水平与下盖板相比要低较多,均在弹性范围内.

图18 典型测点的荷载-应变曲线对比Fig. 18 Load-strain curves of some typical measure points

图19 L1铆钉连接处Mises应力云图Fig.19 Mises stress distribution in area of lockbolts connection of member L1
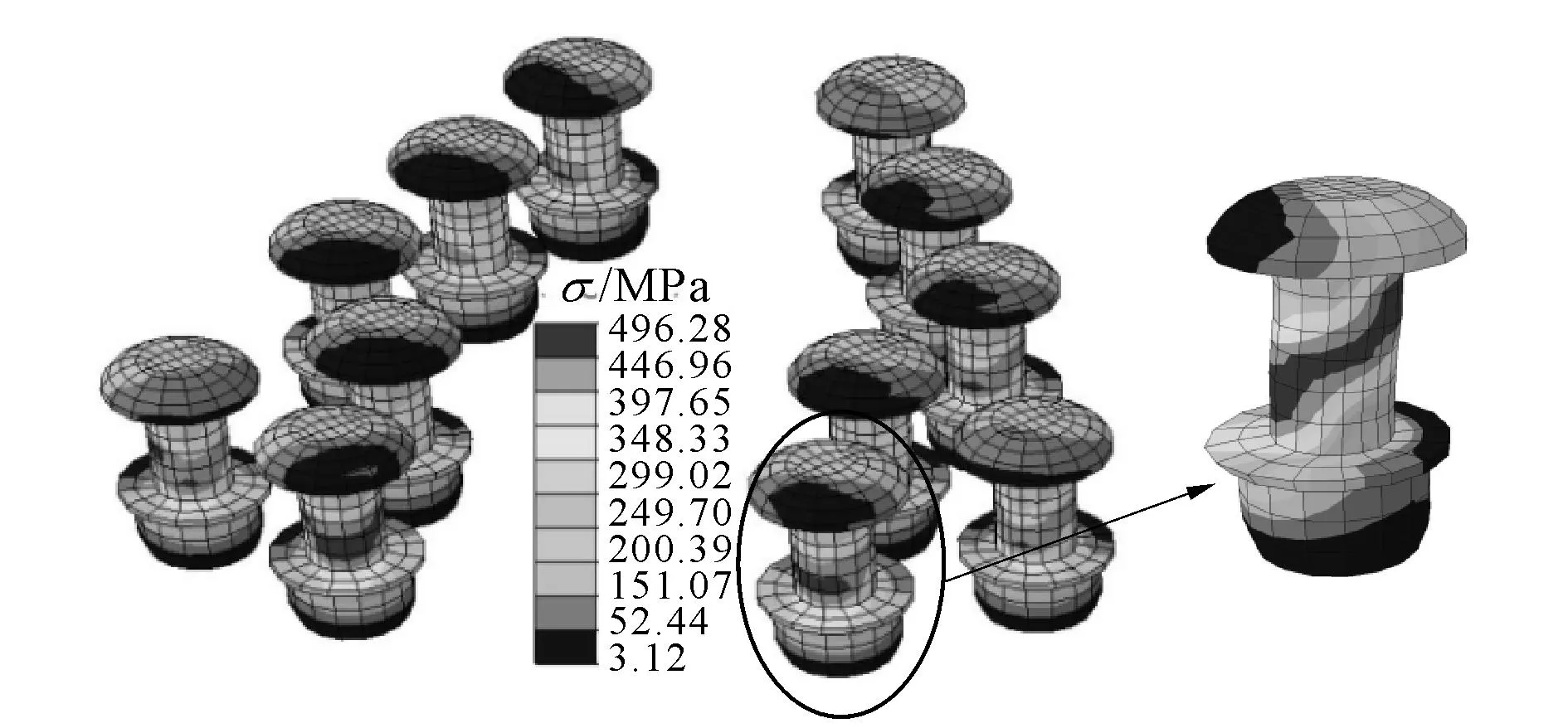
图20 环槽铆钉Mises应力云图Fig.20 Mises stress distribution of lockbolts

图21 盖板Mises 应力云图Fig.21 Mises stresses distribution of cover plates
6结论
(1) 在试验技术方面,两阶段加载方法可以有效模拟以承受弯矩和剪力为主的板式支座节点的受力状态.
(2) 在弯矩和剪力共同作用下,板式支座节点的破坏形式为节点域内工字铝杆件受拉翼缘沿铆钉孔截面的脆性断裂破坏,断裂前没有明显征兆.
(3) 上下盖板的受力存在较大的差异.与工字铝受拉翼缘连接的下盖板应力较高,应力传递路径明显,但分布区域较窄,并未导致盖板发生破坏.上盖板整体的应力水平与下盖板相比要低很多
(4) 受拉翼缘断裂截面处的环槽铆钉受力最为不利,呈拉弯受力状态,但不锈钢的强度较高,也未出现铆钉破坏.
(5) 断裂杆件L1承受的最大弯矩约为工程弯矩设计值的1.86倍,截面纯弯状态下强度设计值的0.9倍.杆件能够承担的最大剪力约为工程剪力设计值的3.56倍.在极限状态下,杆件的剪弯比可达0.30.
(6)板式支座节点的有限元分析结果与试验结果吻合较好,反映了本文的有限元模拟方法有效性.
参考文献(References):
[1] 邓华,陈伟刚,白光波,等. 铝合金板件环槽铆钉搭接连接受剪性能试验研究[J]. 建筑结构学报.2016(01): 143-149.
DENG Hua, CHEN Wei-gang, BAI Guang-bo, et al. Experimental study on shearing behavior of lockbolted lap connection for aluminum alloy plates [J].Journal of Building Structures. 2016(01): 143-149.
[2] 杨联萍,韦申,张其林. 铝合金空间网格结构研究现状及关键问题[J]. 建筑结构学报. 2013, 34(2): 1-19, 60
YANG Lian-ping, WEI Shen, ZHANG Qi-ling. Aluminum reticulated spatial structures: state of the art and key issues [J]. Journal of Building Structures, 2013, 34(2): 1-19, 60.
[3] HWANG K J. Advanced investigations of grid spatial structures considering various connection systems [D]. Stuttgart: University of Stuttgart, 2010: 11-45.
[4] 沈祖炎,郭小农,李元齐. 铝合金结构研究现状简述[J]. 建筑结构学报, 2007, 28(6): 100-109.
SHEN Zu-yan, GUO Xiao-nong, LI Yuan-qi. State of the arts of research on aluminum alloy structures [J]. Journal of Building Structures, 2007, 28(6): 100-109.
[5] GUO Xiao-nong, XIONG Zhe, LUO Yong-feng, et al. Experimental investigation on the semi-rigid behaviour of aluminium alloy gusset joints [J]. Thin-Walled Structures. 2015, 87 (2): 30-40.
[6] GB50429—2007. 铝合金结构设计规范[S]. 北京: 中国计划出版社, 2007:14-17.
GB50429—2007. Code for design of aluminum structures[S]. Beijing: China Planning Press, 2007: 14-17.
[7] 孙训方,方孝淑,关来泰. 材料力学[M]. 北京: 高等教育出版社, 2001:90-124.
[8] RAMBERG W, OSGOOD W R. Description of stress-strain curves by three parameters [R]. Washington DC: National advisory committee for aeronautics, 1943.
[9] MAZZOLANI F M. Aluminum alloy structures [M]. 2th ed. Boca Raton : The Chemical Rubber Company Press, 1994:35-37.
[10] RASMUSSEN K J R. Full-range stress-strain curves for stainless steel alloys [J]. Journal of Constructional Steel Research. 2003, 59(1): 47-61.
[11] 陈伟刚. 平板型铝合金格栅结构板式节点的受力性能研究[D]. 杭州: 浙江大学, 2015: 34-56.
CHEN Wei-gang. Investigation on mechanical behavior of gusset joints of flat aluminum alloy lattice structures [D]. Hangzhou: Zhejiang University, 2015: 34-56.
Load-bearing behavior of bearing joint of flat aluminum alloy lattice structures
CHEN Wei-gang1,2, DENG Hua1,2, BAI Guang-bo1,2, DONG Shi-lin1,2, ZHU Zhong-yi3
(1.SpaceStructuresResearchCenter,ZhejiangUniversity,Hangzhou310058,China;2.ZhejiangProvincialKeyLaboratoryofSpaceStructures,ZhejiangUniversity,Hangzhou310058,China;3.BeijingInstituteofArchitecturalDesign(Group)CompanyLimited,Beijing100045,China)
Abstract:The load-bearing behaviors of bearing joint of flat aluminum alloy lattice structures were investigated by means of finite element analysis and full-scale experiment. The loading test revealed the characteristics of displacement and strain developments of the bearing joint as well as its damage modes. By adopting the finite element analysis, the stress distributions respectively in members, lockbolts and cover plates of the bearing joint were presented. Results show that the outermost row of bolt holes on the tensile flange of aluminum alloy I-beams ruptures and causes the damage of the bearing joint. An obvious high-stress zone exists on the lower cover plate connected with the tensile flange though it is too narrow to induce the fracture of cover plates, while stresses on the upper cover plate are much smaller. The lockbolts in the fracture section of the tensile flange lie in the most unfavorable tensile-bending state, but no damage happens. When the fracture appears in the I-beam, the corresponding ultimate moment is approximately 0.9 times the design strength of aluminum I-beams under pure bending, and the moment-shear ratio reaches 0.3. The results of numerical analysis well coincide with those of the loading test, indicating the validity of the suggested numerical simulation method.
Key words:aluminum alloy structure; flat lattice structure; bearing joint; fracture failure; finite element analysis
收稿日期:2015-05-20.浙江大学学报(工学版)网址: www.journals.zju.edu.cn/eng
作者简介:陈伟刚(1986-),男,博士生,从事空间结构等研究.ORCID: 0000-0001-5025-5421. E-mail: wgchen@zju.edu.cn通信联系人:邓华(1971-),男,教授,博导.ORCID: 0000-0002-0792-0518. E-mail: denghua@zju.edu.cn
DOI:10.3785/j.issn.1008-973X.2016.05.004
中图分类号:TU 395
文献标志码:A
文章编号:1008-973X(2016)05-0831-10
