胎面结构设计参数对轮胎振动噪声的影响

裴晓朋,王国林,周海超,赵　璠

(江苏大学 汽车与交通工程学院,江苏 镇江 212013)



胎面结构设计参数对轮胎振动噪声的影响

裴晓朋,王国林,周海超,赵璠

(江苏大学 汽车与交通工程学院,江苏 镇江 212013)

摘要:为了研究胎面结构设计参数对轮胎振动噪声的影响及降噪机理,以295/80R22.5载重子午线轮胎为研究对象,利用模态声学向量技术对轮胎振动噪声进行模拟分析,采用面板声学贡献度分析方法研究在噪声声压峰值所对应频率下轮胎外轮廓各部件的声学特性,找到胎面为主声学正贡献部件. 选取显著影响胎面结构的参数为设计变量,通过正交试验法分析各参数改变对轮胎振动噪声的影响规律. 结果表明,轮胎振动噪声随带束层端点至旋转轴半径以及胎冠点至旋转轴半径的增大而减小,随带束层压力分布形状系数以及带束层压力分担率的增加先减小后增加. 通过正交试验极差分析得到低噪声轮胎的最优胎面参数组合,并从轮胎各部件对振动噪声的贡献度角度揭示了低噪声轮胎的降低机理.

关键词：载重子午线轮胎；面板声学贡献度；正交试验；振动噪声

噪声污染与大气污染、水污染并列为3大环境污染,交通噪声污染为噪声污染的重要组成部分,受到广泛关注. 高速行驶时的轮胎噪声为汽车噪声的主要来源,当载重车辆行驶在60 km/h以上时,轮胎噪声占整车噪声的30%以上. 欧盟、美国、日本等国家和地区的轮胎标签法以及我国出台的《绿色轮胎技术规范》均对轮胎噪声性能提出了明确的要求及实施期限. 据统计,中国近一半轮胎噪声性能达不到欧盟轮胎标签法的要求. 然而,轮胎噪声的发声机理复杂,受多种因素影响,目前尚未有统一的设计思路来指导低噪声轮胎设计[1].

Ruhala等[2]采用实验方法指出在频率为600 Hz以下胎侧振动是轮胎振动噪声的主要原因. Takayuki等[3]采用声全息技术确定了在频率为500 Hz以下轮胎胎侧振动是滚动轮胎辐射噪声的主要因素. Lopez等[4]建立了轮胎滚动过程中的动态模型,模拟了轮胎的低频振动特性,预测了轮胎滚动过程中的动态响应. 法国Perlsse[5]进行了滚动轮胎径向振动实验,并且计算了轮胎在静态载荷作用下,纯滚动状态下接地印迹长,表明了胎面和胎侧振动为相干源. 张涛[6-9]运用有限元和边界元法相结合的方法,对轮胎的结构振动噪声进行研究,提出了在频域上计算轮胎振动噪声的方法,并分析了运行参数和结构参数对轮胎结构振动噪声频率和空间分布特性的影响. 但以往研究只定性的得出胎面和胎侧振动是滚动轮胎产生噪声的主要原因,尚未定量分析胎面和胎侧的振动对轮胎振动噪声的贡献程度,且对低噪声轮胎结构优化及其降噪机理研究尚不充分.

本文以载重子午线轮胎295/80R22.5为研究对象,利用模态声学传递向量技术模拟分析轮胎振动噪声以及轮胎外轮廓各部件对其的声学贡献度. 利用正交试验方法分析影响胎面结构设计的4个设计参数改变对轮胎振动噪声的影响规律,并得到使轮胎振动噪声值最小的最优胎面设计参数组合. 在此基础上,从轮胎外轮廓声学贡献角度分析轮胎振动噪声降低的原因,从而为低噪声轮胎结构设计提供参考依据.

1理论基础

由运动学方程、连续性方程和物态方程可以得到声波的线性方程：

(1)

式中：▽2为Laplace算子,c为流体介质中的声速,p为声压,t为时间.

在线弹性流体介质内,声压p应满足Helmholtz微分方程：

▽2p+k2p=0.

(2)

式中：k=ω/c,ω为声源简谐振动圆频率.

和流固界面条件：

(3)

式中：i为虚数单位,ρ为密度,n为边界面的外法向，vn为结构表面指向流体域的法向振速．

以及Sommerfeld辐射条件：

(4)

式中：r为空间声场内任意的场点.

Helmholtz微分方程的基本解为

G(Q,P)=exp(-ikr)/4πr .

(5)

结合方程(1)、(2)、(3)、(4)、(5),可得到声场中任一点P处采用单层势ξ和双层势μ表示的间接积分方程：

(6)

式中：Q为结构表面内的任意点,单层势ξ为结构表面的速度差,双层势μ为声学边界表面的声压差s为结构表面.

2轮胎振动噪声仿真分析

2.1轮胎有限元分析模型建立

以某公司生产的295/80R22.5载重子午线轮胎为研究对象,利用ABAQUS软件,采用文献[10]中的方法建立带纵沟花纹的轮胎三维有限元模型,如图1所示. 橡胶部分采用CGAX3和CGAX4R单元模拟,钢丝帘线采用SFMGAX1和REBAR单元模拟.

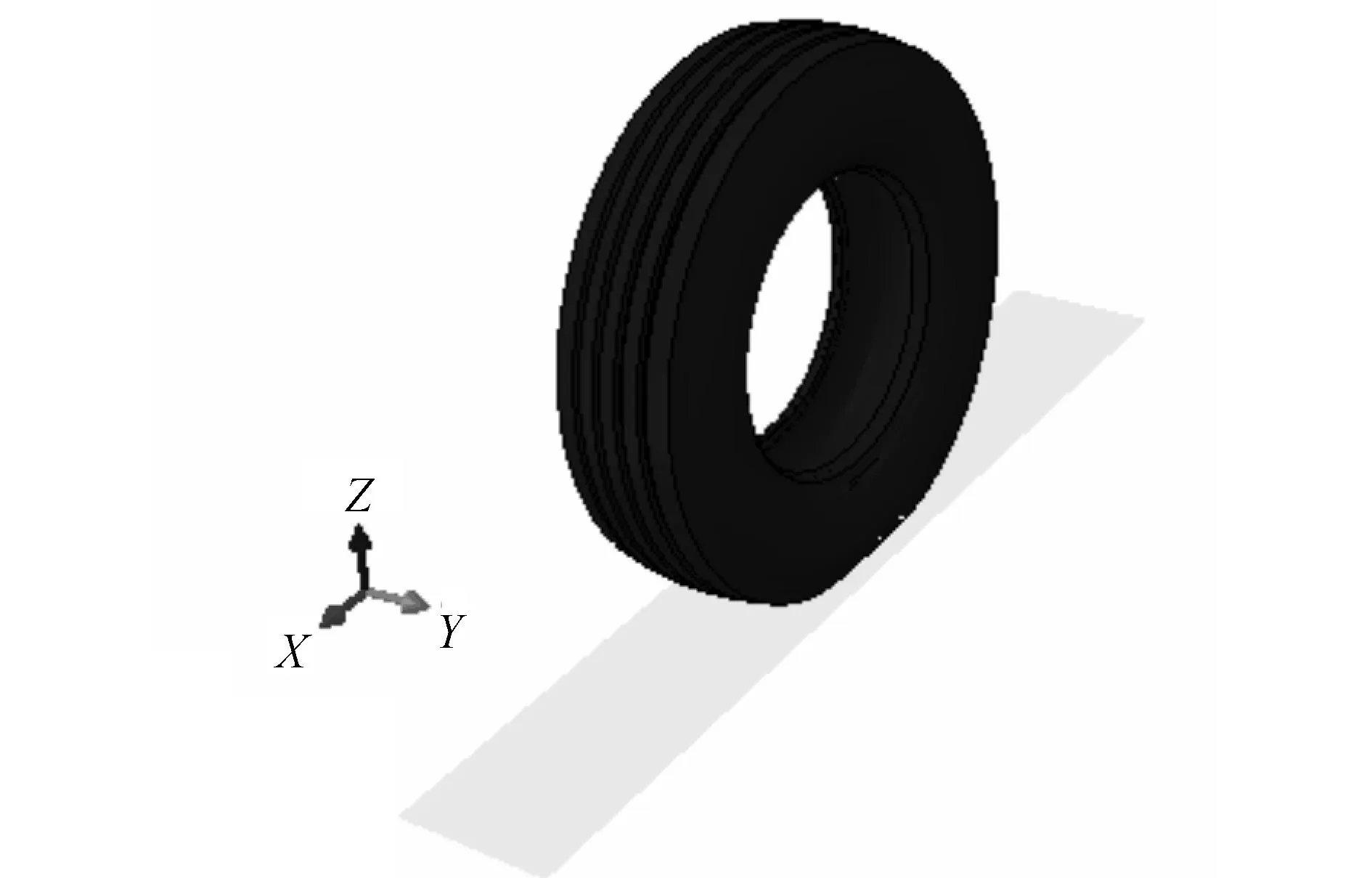
图1　轮胎三维有限元模型Fig.1　Three dimensional tire finite element model

橡胶本构模型的选取对提高模拟分析方法的计算精度、保证大变形分析过程中橡胶单元保持良好的形态、避免发生体积自锁现象具有重要作用. 将测得的橡胶的拉伸数据输入ABAQUS软件,并利用其自带的OGDEN、Neo-hookean和Yeoh等橡胶本构模型分别进行拟合. 以胎肩垫胶为例,其材料应力σ和应变ε曲线拟合如图2所示.

图2　不同本构模型的胎肩垫胶拟合曲线Fig.2　Fitting curves of tire shoulder rubber for different constitutive models

由图2中可以看出,在名义应变小于0.5的范围内,Yeoh本构模型可以较好地拟合试验数据,因此本文选用Yeoh模型描述轮胎胶料的力学特性. 轮胎各部位的胶料参数由单轴拉伸试验数据拟合获得.

参照文献[10]的方法对轮胎进行加载分析,载荷为额定载荷3 550 kg,气压为额定气压0.9 MPa. 在ABAQUS软件中完成对轮胎的装配、充气、加载和稳态自由滚动分析.

2.2轮胎模态试验及有限元分析

模态分析是一种以试验为基础的结构动态特性分析方法,为验证轮胎有限元模型建立的正确性,采用法国OROS公司的动态试验设备进行轮胎的模态试验. 在试验过程中,轮胎处于自由悬置状态,如图3所示,轮胎表面布置81个均布的测点.

图3　轮胎模态试验实物图Fig.3　Scheme of tire mode test

本次试验采用锤击法激励,利用加速度传感器测量响应信号. 将激励和响应信号放大后输入动态分析仪,分析处理得到0～200 Hz传递函数,每测点锤击3次,经线性平均后将该点的传递函数保持到计算机中. 由模态分析软件得到轮胎自由悬置状态下前六阶固有频率和振型如图4所示.

轮胎自由模态的有限元分析采用Block Lanczos法,并将有限元分析得到的前六阶模态固有频率仿真值fβ和试验测试得到的前六阶模态固有频率试验值fγ进行对比,两者之间的误差用ζ表示,对比如表1所示,其中j为模态阶次.

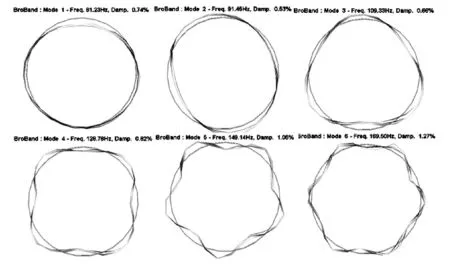
图4　轮胎前六阶模态振型图Fig.4　Mode shape of tire first 6th mode

Tab.1Comparison of tire natural frequency of former six modal

jfγ/Hzfβ/Hzζ/%181.2359.1727.2291.4576.1516.73109.3396.7511.54128.78117.628.75149.14136.726.26169.5152.2510.2

由表1可知,轮胎有限元模型能较好的计算出轮胎的各阶模态. 计算模态频率普遍比试验模态偏低,其中前2阶模态固有频率相对误差较大,第3阶到第6阶模态的固有频率的相对误差在10%左右.

轮胎前6阶模态固有频率的试验值与仿真值对比曲线fα-j如图5所示,由图5中可以看出,试验值与仿真值却有很好的一致性.

图5　轮胎前六阶模态固有频率对比Fig.5　Comparison of tire natural frequency of former six modal

这主要是因为建立轮胎有限元分析模型时,对其结构进行了简化,且忽略了轮辋,导致轮胎质量降低. 根据质量与固有频率的关系,质量越小,固有频率应越高,但轮胎质量的减小同时也减小了轮胎胎体刚度,且对胎体刚度的影响大于对质量的影响. 因此,轮胎有限元模态分析的固有频率小于轮胎模态试验测得的固有频率.

综合考虑上述因素,可以得出该数值仿真模型具有一定的可靠性.

2.3轮胎振动噪声数值分析

2.3.1轮胎声学边界元模型建立将受载变形状态下的轮胎有限元模型导入到Hypermesh中提取面网格,为了避免声能量泄露,在轮辋处设置圆形区域将声学边界元模型封闭起来,建立轮胎声学边界元分析模型,如图6所示.

图6　轮胎声学边界元分析网格Fig.6　Mesh used for BEM calculation

模型共16 440个单元,16 434个节点. 该模型的节点与滚动分析的有限元模型相应的节点号和节点坐标完全一致. 从而保证了有限元振动信号传递到边界元网格的准确性.

考虑到轮胎的对称性,根据GB/T3767-1999《声学-声压法测定噪声源声功率级-反射面上方近似自由场的工程法》,在其周围建立半径为1 m的半圆罩型模型,该模型定义了19个声学观测点. 分析时定义路面为刚性反射面. 轮胎振动噪声声压值通过声压叠加的方法计算场点网格19个观测点的A计权声压均值. 通过计算分析得知,场点网格上的19个声学测点的声压频响函数曲线变化趋势一致,只是声压值的大小不同. 不失一般性,本文通过观测场点网格上声学观测点,分析轮胎外轮廓结构各部件的声学贡献度. 声学分析模型与声学观测点如图7所示.

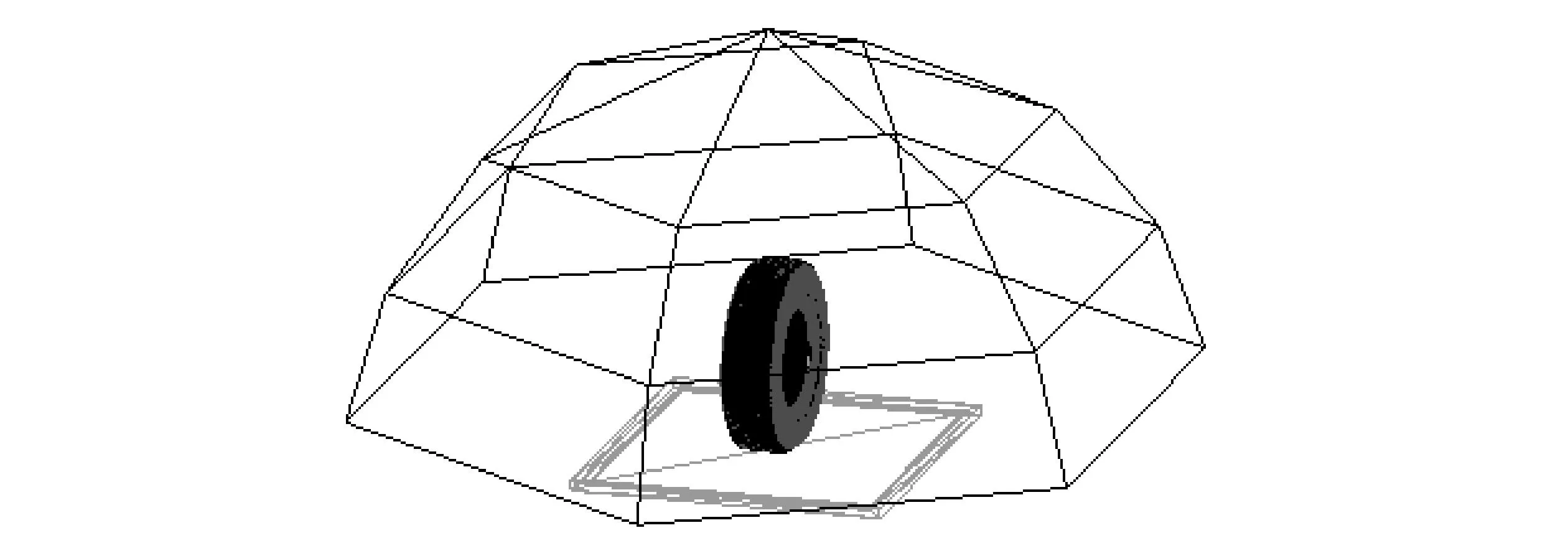
图7　声学模型与声学观测点Fig.7　Acoustic model and Acoustic study point

2.3.2轮胎振动噪声数值分析合理选取路面激励对准确预测轮胎振动噪声具有重要作用. 本文利用ABAQUS隐式向显式传输功能,在ABAQUS/Explicit模拟轮胎滚动分析,所得的路面激励作为轮胎振动噪声计算的输入激励. 提取轮胎在路面稳态滚动一周后的径向力作为激励,径向力F随时间t的变化如图8所示.

图8　时域内轮胎与路面径向激励力Fig.8　Excitation force between tire and road in time domain

在此基础上,对径向激励力进行傅里叶变换,得到轮胎振动噪声计算所需的频域上的激励力,如图9所示.

图9　频域内轮胎与路面径向激励力Fig.9　Excitation force between tire and road in frequency domain

以此力作为激励力施加在轮胎与路面接触的中心点,导入轮胎模态分析结果求其模态参与因子. 在声压求解过程中,通过数据转移将轮胎表面节点信息映射到声学网格上,运用模态声学传递向量技术计算原始设计20 Hz到500 Hz轮胎振动噪声值为78.79 dB. 场点网格观测点处的声压级Lp与频率f之间的关系,如图10所示.

图10场点声压频响函数曲线Fig.10　Field sound pressure frequency response function curve

从图10分析可知,295/80R22.5型全钢载重子午线轮胎现形设计主要声压峰值所对应的频率为116、146 、296、338 、374 Hz.

3轮胎外轮廓声学贡献度分析

3.1面板声学贡献度分析方法

面板声学贡献度分析方法能够量化每个结构部件对辐射噪声的贡献程度,并且已经广泛应用于汽车行业中[11].

当某个部件的声学贡献相位与总的声学贡献的相位一致,并且该部件的声压贡献幅值最大,称为主最大声学正贡献部件. 当某个部件的声学贡献相位与总的声学贡献相位相反时,并且该部件的声压贡献最大,称为主最大负贡献部件. 所以,在进行结构修改前,确定对轮胎外辐射声场贡献较大的轮胎外轮廓部件,并采取相应的控制策略,取得的降噪效果最理想.

3.2轮胎外轮廓声学贡献度分析模型建立

为定量分析在如图10所示5个峰值频率下,轮胎外轮廓各部位对轮胎振动噪声的贡献大小,将载重子午线轮胎295/80R22.5的外轮廓分成了6个部件,分别定义为胎面(Tread)、上胎侧(Side-upper)、中胎侧(Side-middle)、下胎侧(Side-lower)、耐磨橡胶(Abrasion)和轮辋部件(Yuan),如图11所示.

1- 胎面； 2-上胎侧 ；3-中胎侧； 4-下胎侧 ；5-耐磨橡胶； 6-轮辋区域图11　轮胎外轮廓各部件模型Fig.11　Tire outer contour panel model

3.3轮胎外轮廓声学贡献度分析

从图10中可以看出在频率f=116、146、296、338、374 Hz时,声压出现较为明显的峰值. 因此,降低轮胎的振动噪声,可降低对应频率下主最大声学正贡献部件的噪声. 轮胎外轮廓各部件l在f=116、146、296、338、374 Hz 处峰值频率下的声压幅值Lp和相位θ贡献直方图如图12所示.

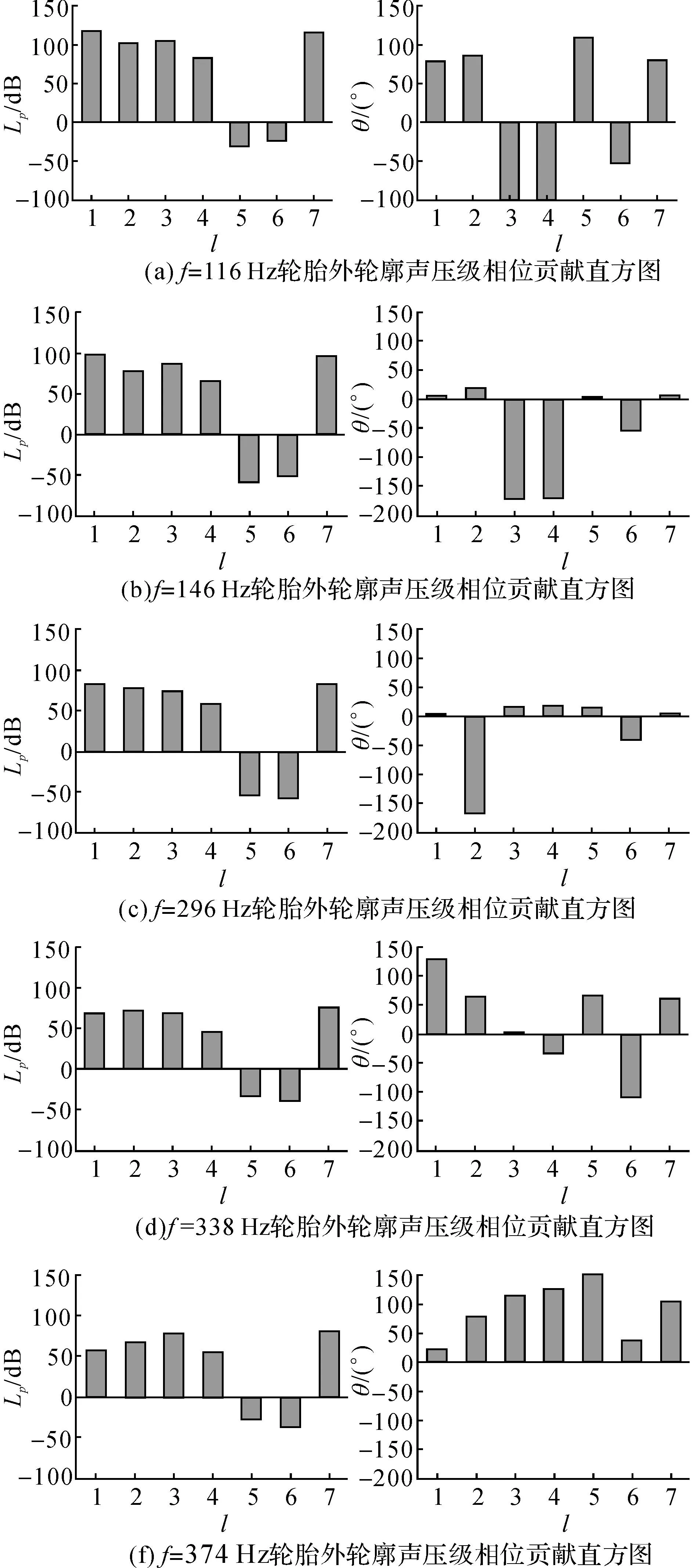
图12　轮胎外轮廓部件声学贡献度Fig.12　Tire outer contour panel acoustic contribution

由图12可知,在f=116 Hz时,Tread、Side-upper和Abrasion为正贡献部件,并且Tread的声压幅值贡献最大,为主最大正贡献部件. 而Side-middle、Side-lower和Yuan的相位贡献与总的相位相反,是负贡献部件；在f=146 Hz时,Tread、Side-upper和Abrasion部件的相位与总的贡献相位一致,为声学正贡献部件. Tread声压幅值最大,是主最大声学正贡献部件. 而Side-middle、Side-lower和Yuan的相位贡献与总的相位相反,是声学负贡献部件；在 f=296 Hz时,Tread、Side-middle、Side-lower和Abrasion的相位与总的贡献的相位一致,都是声学正贡献部件. Tread的声压幅值最大,是主最大声学正贡献部件. 而Side-upper和Yuan的相位与总的贡献相位相反,为负贡献部件；在f=338 Hz时,Tread、Side-upper和Abrasion的相位与总的贡献的相位一致,都是声学正贡献部件. 而Side-middle、Side-lower和Yuan的相位与总的贡献相位相反,为声学负贡献部件；在f=374 Hz时,轮胎外轮廓各部件的相位与总的贡献相位一致,都是正贡献部件. 综上所示,在5个峰值频率下胎面和耐磨胶为声学正贡献部件,而胎面的声压幅值较大. 因此,分析胎面结构对轮胎振动噪声的影响具有重要意义.

4胎面结构参数对轮胎振动噪声的影响

4.1试验方案设计

正交试验能够有效的研究多因素多水平的设计方法,并已用于轮胎外轮廓设计参数的优化中[12]. 为分析胎面结构参数对轮胎振动噪声的影响,选取显著影响轮胎胎面结构设计参数的带束层端点至旋转轴半径rd(mm)、带束层压力分布形状系数α、带束层压力分担率τ0和胎冠点至旋转轴半径rk(mm)为设计变量[13],其中带束层压力分布形状系数是指带束层压力分担率的分布形状,当α=0时,表明带束层压力分担率的分布是均匀的；当α=0.625时,表明带束压力分担率是呈抛物线形状分布；当α=0.375时,表明带束层压力分担率的分布是介于两者形状之间的分布. 带束层压力分担率是指带束层与胎体接触面上的接触压力通常可以代表带束层对充气压力的分担程度,可以表示为

(7)

式中：σn为带束层与胎体层之间的法向接触应力,pλ为充气压力.

研究以上参数对轮胎振动噪声的影响,设计参数如图13所示.

图13　设计参数示意图Fig.13　Design parameters

选用正交表L9(34)安排试验,每个因素3个水平,如表2所示为正交试验因素水平表.

表2　因素水平

利用正交试验表安排试验方案,并利用本文方法对各方案的轮胎振动噪声进行计算,其结果如表3所示.

表3　实验正交表L9(34)及试验结果数据

4.2极差分析

为分析rd、α、τ0、rk设计参数对轮胎振动噪声的影响,根据表3的试验结果,建立极差分析,结果如表4所示. 表中：Lp1为不同水平情况下对应的声压级的平均值，Rj为极差,通过Rj的大小可以判断各因素对轮胎振动噪声的影响的主次顺序. 由表4可知，胎冠点至废转轴半径对轮胎振动噪声的影响最为显著，其次为带束层压力分布形状系数、带束层压力分担率和带束层端点至旋转轴半径.此外，通过对比不同水平情况下对应的轮胎振动噪声声压级平均值的大小，可以确定各因素的优水平，即rd=487.13 mm,α=0.2、τ0=0.8、rR=495.94 mm时轮胎振动噪声声压级值最小.利用本文提出的方案对最优组合方案的轮胎振动噪声进行计算，其值为75.27 dB,降噪量达3.5 dB.

表4　综合评判极差分析结果

图14　声压均值主效应图Fig.14　Main effects plot of Mean Sound Stress

为进一步研究这4个设计参数对轮胎振动噪声的影响规律,如图14所示为各设计参数对振动噪声的影响.

由图14可知,轮胎振动噪声随带束层端点至旋转轴半径以及胎冠点至旋转轴半径的增大而减小；轮胎振动噪声随带束层压力分布形状系数以及带束层压力分担率的增加先减小后增加,两者之间存在使轮胎振动噪声为最小的值.

4.3降噪机理分析

为分析结构优化后轮胎的振动噪声降低原因,对优化前后轮胎外轮廓的声学贡献度进行了对比,结果如图15所示.

图15　峰值频率下轮胎外轮廓声学贡献度对比Fig.15　Comparison of tire outer contour panel acoustic contribution at five peak frequency

从图15中可以看出,在f=116 Hz时,优化后的轮胎外轮廓结构降低了声学正贡献部件Tread、Side-middle和Side-lower的声压幅值贡献,同时Side-upper、Abrasion和Yuan部件变为声学负贡献部件；在f=146 Hz时,优化后的轮胎外轮廓结构降低了Tread、Side-upper和Side-middle部件的声学正贡献部件的声压幅值,Side-lower变为声学负贡献部件；在f=296 Hz时,优化后的轮胎外轮廓结构降低了声学正贡献部件Tread和Side-lower的声压幅值贡献,Side-upper和Side-middle变为声学负贡献；在f=338 Hz时,优化后的轮胎外轮廓结构降低了声学正贡献部件Tread的声压幅值贡献,Side-upper和Side-middle变为声学负贡献部件；在f=374 Hz时,优化后的轮胎外轮廓结构降低了声学正贡献部件Side-upper、Side-lower的声压幅值贡献,Side-middle和Yuan变为负贡献部件. 通过对比分析优化前后轮胎外轮廓声学贡献度可以看出,优化后的轮胎结构降低了主最大声学正贡献部件胎面的声压幅值. 同时也增加了轮胎外轮廓结构声学负贡献部件的数量,进而降低了轮胎振动噪声.

5结论

(1)在选取的影响胎面结构设计的4个设计参数中,轮胎振动噪声随着带束层端点至旋转轴半径以及胎冠点至旋转轴半径的增大而减小；轮胎振动噪声随着带束层压力分布形状系数以及带束层压力分担率的增加先减小后增加；

(2)通过结构优化设计能够改变轮胎外轮廓的声学贡献特性,降低轮胎振动噪声；

(3)本文仅针对风神轮胎股份有限公司生产的295/80R22.5型载重子午线轮胎进行研究,研究对象相对较少. 在接下来的研究中,将增加轮胎的数量和类型,通过多组统计分析得出适合轮胎振动噪声的普适性结论,从而指导低噪声轮胎结构设计；

(4)本文只是通过轮胎外轮廓声学贡献度方法分析得到轮胎胎面为主声学正贡献部件,并没有从内部结构分析其原因. 在接下来的课题研究中,将从内部结构对轮胎振动噪声的贡献度分析,揭示其产生的原因；

(5)由于试验条件的限制,本文未能对新设计的轮胎样品进行噪声测试,但是目前已经完成样胎的试制,准备送往欧洲进行轮胎室外通过噪声测试.

参考文献(References):

[1] GARG N,MAJI S. A critical review of principal traffic noise models: Strategies and Implications [J]. Environmental Impact Assessment Review,2014,46(4)：68-81．

[2] RUHALA R J. A Study of tire/pavement interaction noise using near-field acoustical holography[D]. Pennsylvania:The Pennsylvania State University,2000．

[3] KOIZUMI T,TSUJIUCHI N,TAMAKI R,et al. An analysis of radiated noise from rolling tire vibration [J]. Jsae Review, 2003,24(4)：465-469．

[4] LOPEZ I,BLOM R E A,ROOZEN N B,et al. Modelling vibrations on deformed rolling tires—a modal approach [J]. Journal of Sound and Vibration,2007,307(3)：481-494．

[5] PERISSE J. A study of radial vibration of a rolling tire for tire/road noise characterization [J]. Mechanical Systems and Signal Processing,2002,16(6)：1043-1058．

[6] 张涛. 轮胎模态和振动噪声的数值分析[D]. 合肥：中国科学技术大学,2005．

ZHANG Tao. Numerical analysis of tire modal and vibration noise[D]. Hefei∶University of Science and Technology of China, 2005．

[7] 包秀图,张涛,李子然,等. 轮胎振动噪声的数值模拟[J]. 振动与冲击,2008,27(11)：6-11．

BAO Xiu-tu,ZHANG Tao,LI Zi-ran,et al. Numerical Simulation of tire vibration noise [J]. Journal of Vibration and Shock,2008, 27(11)：6-11．

[8] 包秀图. 不同工况和结构参数对轮胎振动噪声影响的数值分析[D]. 合肥：中国科学技术大学,2008．

BAO Xiu-tu. Numerical analysis of influence of different operation condition and structure parameters on tire vibration noise[D]. Hefei:University of Science and Technology of China,2008.

[9] 常亮,肖旺新,谢伟平. 轮胎振动声辐射数值分析[J]. 噪声与振动控制,2010,1(3)：85-90．

CHANG Liang,XIAO Wang-xin,XIE Wei-ping. Numerical analysis of vibration and sound radiation of tires [J]. Noise and Vibration Control,2010,1(3)：85-90.

[10] 梁晨. 子午线轮胎综合接地性能评价体系研究[D]. 镇江：江苏大学,2013．

LIANG Chen. Research on radial tire comprehensive ground performance evaluation system and method[D].Zhenjiang∶Jiangsu University,2013．

[11] 罗斌. SFM05型地铁动车噪声预测及声学贡献度分析[D]. 长沙：中南大学,2010．

LUO Bin. SFM05 type metro noise prediction and acoustic contribution analysis[D]. Changsha:University of Central South, 2010．

[12] KIM S R,SUNG K D,LEE D W,et al. Cavity noise sensitivity analysis of tire contour design factors and application of contour optimization methodology [J]. Journal of Central South University(English Vision),2012∶19(8)：2386-2393.

[13] 王国林,万治君,梁晨, 等. 基于非平衡轮廓理论的子午线轮胎结构设计[J]. 机械工程学报,2012,24(48)：112-118.

WANG Guo-lin,WAN Zhi-jun,LIANG Chen,et al. Structural design of radial tire based on non-balanced outline theory [J]. Journal of Mechanical Engineering,2012,22(48)：112-11.

Influence of tread design parameters on tire vibration noise

PEI Xiao-peng,WANG Guo-lin,ZhOU Hai-chao,ZhAO Fan

(SchoolofAutomotiveandTrafficEngineering,JiangSuUniversity,Zhenjiang212013,China)

Abstract:The radial heavy duty tire 295/80R22.5 was taken as the object of the research, in order to research the effects of tread design parameters on tire vibration noise and the mechanism of noise reduction. Tire vibration noise was computed by using modal acoustic transfer vector technolog. Then the acoustic characteristics of tire outer contour panels at the peak frequency was analyzed using acoustic contribution method. Tread is the main acoustic positive panel. Parameters influence tire tread design were selected to analyze the effect of these parameters on tire vibration noise by orthogonal method. Results show that the tire vibration noise decreases;with the increase of the radius of the belt layer to the axis of rotation and the radius of tire tread to the axis of rotation, with the increase of the shape coefficient of belt layer pressure rate and the belt layer pressure rate, the tire vibration noise decreases at first and then increase. The optimal tread parameters of the low-noise were obtained by the orthogonal test range analysis. The reasons why the tire vibration noise was reduced were studied by means of acoustic contribution．

Key words:heavy duty radial tire; acoustic contribution; orthogonal test; vibration noise

收稿日期：2015-05-30.浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

基金项目：国家自然科学基金资助项目(51405201)；江苏省汽车工程重点实验室开放基金项目资助(QC201303)；江苏省2013年度普通高校研究生创新计划资助项目(CXLX13_676).

作者简介：裴晓朋(1991-)，男，硕士生，从事现代汽车轮胎结构设计等研究.ORCID：0000-0002-5475-038X. Email：pxp@ujs.edu.cn通信作者：王国林，男，教授，博导.ORCID：0000-0001-6936-6535. Email：glwang@ujs.edu.cn

DOI:10.3785/j.issn.1008-973X.2016.05.009

中图分类号：U 463.341

文献标志码：A

文章编号：1008-973X(2016)05-0871-08