基于MRT-LBM方法的大规模可扩展并行计算研究

刘智翔　方　勇　宋安平　徐　磊　王晓伟2,　周丽萍2,　张　武2,

1(上海大学通信与信息工程学院　上海　200444)2(上海大学高性能计算中心　上海　200444)3(上海大学计算机工程与科学学院　上海　200444)(zxliu@shu.edu.cn)

基于MRT-LBM方法的大规模可扩展并行计算研究

刘智翔1,2方勇1宋安平3徐磊3王晓伟2,3周丽萍2,3张武2,3

1(上海大学通信与信息工程学院上海200444)2(上海大学高性能计算中心上海200444)3(上海大学计算机工程与科学学院上海200444)(zxliu@shu.edu.cn)

摘要在大规模三维复杂流动的数值模拟中，针对具有良好数值稳定性的多弛豫时间模型格子Boltzmann方法(MRT-LBM)，并结合大涡模拟湍流模型和曲面边界插值格式，分析了在D3Q19离散速度模型下的网格生成、流场信息初始化和迭代计算3部分的可并行性.采用MPI编程模型，从分布式集群的特点和计算量负载均衡的角度出发，分别提出了适合于大规模分布式集群的网格生成、流场信息初始化和迭代计算的并行算法.该并行算法也能有效适用于D3Q15和D3Q27离散速度模型.通过在国产神威蓝光超级计算机上的测试，分别针对求解问题总体计算规模固定和保持每个计算核中计算量一致的2种情况的并行性能分析，验证了该并行算法在十万计算核的量级下仍具有良好的加速比和可扩展性.

关键词大规模并行计算；可扩展；负载均衡；格子Boltzmann方法；多松弛时间模型；大涡模拟

复杂流体运动的数值模拟一直是大规模科学与工程计算中最重要且具有挑战性的研究领域之一.与基于宏观Navier-Stokes方程的计算流体动力学和基于微观分子动力学的流体力学模拟方法不同，格子Boltzmann方法(lattice Boltzmann method, LBM)从介观尺度来描述流体系统[1-2]，由于Boltzmann方程自身本质的运动学特性，以及可以根据经典的Chapman-Enskog展开从LBM得到Navier-Stokes方程，使得LBM比基于连续介质假设的Navier-Stokes方程包含了更多的物理内涵.同时LBM可以看成是Navier-Stokes方程差分法逼近的一种无条件稳定的格式[2].在LBM中没有基于连续介质的假设，而是把流体看成是由许多只有质量没有体积的微粒所组成,这些微粒可以向空间若干个方向任意运动.通过其质量、动量、能量守恒原理，建立表征质点在给定的时刻位于空间某一个位置附近的概率密度函数，再通过统计的方法来获得质点微粒的概率密度分布函数与宏观运动参数间的关系.利用这种简化的运动学方程形式，既可以避免求解含有复杂碰撞项的完整积分-微分Boltzmann方程，又可避免对流场中的每个分子进行大规模计算.由于LBM具有算法简单、计算效率高、并行性好以及能够方便处理复杂边界条件等优点，所以其非常适合处理复杂几何形状和复杂流动大规模计算问题[3].

目前，常用的LBM方法中主要采用3种碰撞模型：单弛豫时间(single-relaxation-time, SRT)[4-5]、多弛豫时间(multiple-relaxation-time, MRT)碰撞模型[6-8]和熵模型(entropic)[9].SRT碰撞模型只有一个弛豫时间可调，而MRT模型是将碰撞过程通过线性变换转换到矩空间中进行，且更好地考虑了实际流动中的各向异性和计算条件的参数优化，具有多个可调的弛豫时间.文献[6]针对方腔流问题，从数值稳定性和精度等角度对这3种碰撞模型进行了详细分析，分析出MRT碰撞模型具有更好的数值稳定性和精度.而在针对湍流问题的数值模拟中，由于问题本身的复杂性和具有高雷诺数，直接使用LBM进行数值模拟无法准确进行计算，常需要将大涡模拟湍流模型引入到计算中[10].Krafczyk等人[11]将Smagorinsky涡粘性模型与D3Q15的MRT-LBM进行耦合计算，对槽道中物体绕流进行了大涡模拟研究.Menon等人[12]将局部动力亚格子应力模型引入SRT-LBM对三维合成射流和自由射流进行了数值模拟.Leila等人[13]对LBM在湍流数值模拟中的应用进行了详细总结，证明了结合大涡模拟湍流模型的MRT-LBM进行湍流的模拟具有更好的数值稳定性.

对于复杂流动问题的计算，LBM往往需要大规模的笛卡儿网格才能准确进行数值模拟，这时高性能计算将是一种较好的解决办法.目前，高性能计算集群大多采用分布式结构，在不同的计算节点间采用消息传递接口(message passing interface, MPI)进行通信.而千万亿次的超级计算机(天河、曙光星云、神威)通常都具有数十万、百万的计算核，充分发挥大规模计算核的优势来加速问题的求解，需要研究具有良好可扩展性的高效并行程序[14].考虑到LBM适合于大规模计算的优点和高性能计算机的特点，本文将针对MRT-LBM方法，并结合大涡模拟、曲面边界插值格式和笛卡儿网格生成，研究能够求解实际流动问题、具有高可扩展的MRT-LBM并行算法.

1多弛豫时间的格子Boltzmann方法

本节主要介绍在三维情况下基于D3Q19离散速度模型的多弛豫时间格子Boltzmann方法、大涡模拟湍流模型和曲面边界的插值格式.

1.1MRT-LBM

格子Boltzmann方法是一种介观方法，它包括3部分：粒子分布函数、离散速度模型和分布函数的演化模型.LBM的分布函数演化模型[7]可表示为

fi(x+ξiδt,t+δt)-fi(x,t)=Ωi,

(1)

其中，fi是粒子分布函数，Ωi是碰撞项，δt是时间步长，ξi是第i个方向的离散速度.由于本文针对的是实际流动问题的数值模拟，所以仅考虑三维情况.

文中使用D3Q19离散速度模型进行描述，其离散速度(如图1所示)为

(2)

其中,c是格子声速，其值为c=δxδt=1.碰撞项Ωi通常有3种：单弛豫时间、多弛豫时间和熵模型.在MRT模型中，碰撞是在矩空间中进行，则碰撞项可以表示为

Ωi=-{M-1·S·[m(x,t)-meq(x,t)]}i，

(3)

其中，M是变换矩阵，meq是矩空间的平衡态函数，其具体值可见文献[7].S是对角矩阵，其值为

S=diag(0,s1,s2,0,s4,0,s4,0,s4,s9,

s10,s9,s10,s13,s13,s13,s16,s16,s16).

(4)

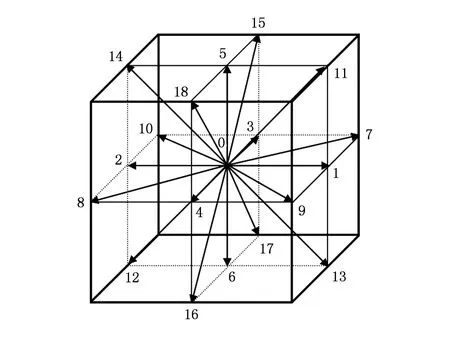
Fig. 1　The D3Q19 velocity model.图1　D3Q19离散速度模型

弛豫参数s9和s13满足：

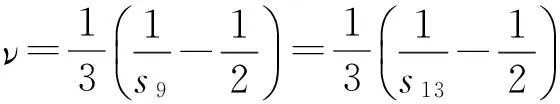
(5)

这里ν是粘性系数.其余的弛豫参数可根据文献[8]取为s1=1.19，s2=s10=1.4，s4=1.2，s16=1.98.根据上面的描述，MRT-LBM的计算过程可以分为2部分：

1) 碰撞过程:

{M-1·S·[m(x,t)-meq(x,t)]}i；

(6)

2) 迁移过程:

(7)

1.2大涡模拟湍流模型

为了准确模拟高雷诺数湍流运动中的情况，可以在MRT-LBM中引入大涡模拟亚格子模型，文中采用常用的Smagorinsky涡粘模型[15]，其引入的方式是通过改变原来的弛豫时间来实现(即修改式(5)中的粘性系数)，引入大涡模拟后的有效粘性变为

ν=ν0+νt，

(8)

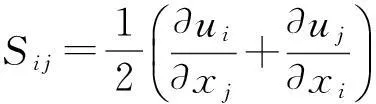
νt=(CsΔ)2|S|,

(9)

这里，Cs是Smagorinsky参数，|S|为应变率张量Sij的模.因此，在MRT-LBM中引入的大涡模拟湍流模型仅需要在每次碰撞时按照式(8)(9)调整弛豫参数s9和s13.

1.3曲面插值格式

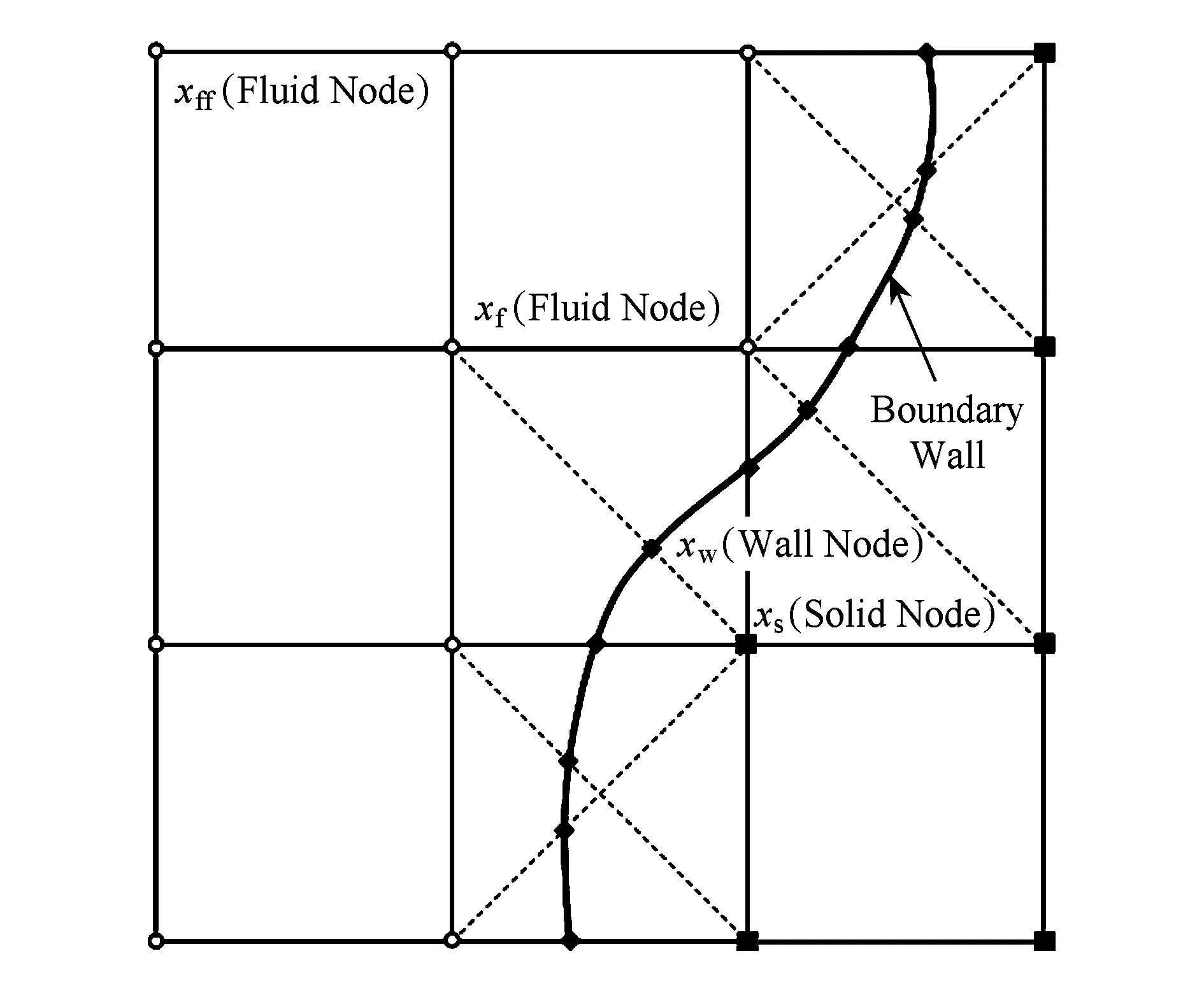
Fig. 2　Layout of the regularly spaced lattices and curved wall boundary.图2　网格点和曲面边界的布局图

在三维复杂几何的数值模拟中，由于MRT-LBM采用的是统一尺度的笛卡儿网格，网格点无法保证恰好在曲面边界上，因此需要构造一种插值格式来处理曲面边界上的网格点.为了便于描述插值格式，这里给出二维情况下的曲面边界示意图，如图2所示：

在MRT-LBM中，我们先将所有的网格点分为3类：流体网格点xf(fluid node)、曲面边界网格点xw(boundary wall node)和几何体内部网格点xs(solid node).由于几何体内部的网格点在物体内部，所以不需要计算.流体网格点和曲面边界网格点需要计算.因此，需要在曲面边界网格点上进行插值以获得D3Q19离散速度方向上的全部未知粒子分布函数.本文采用文献[16]中的YMS曲面插值格式处理曲面边界网格点xw，其具体插值格式为

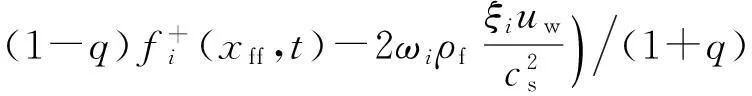
(10)

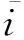
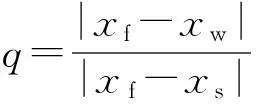
(11)

2MRT-LBM高可扩展并行算法

根据第1节中的内容，MRT-LBM的计算流程如图3所示：

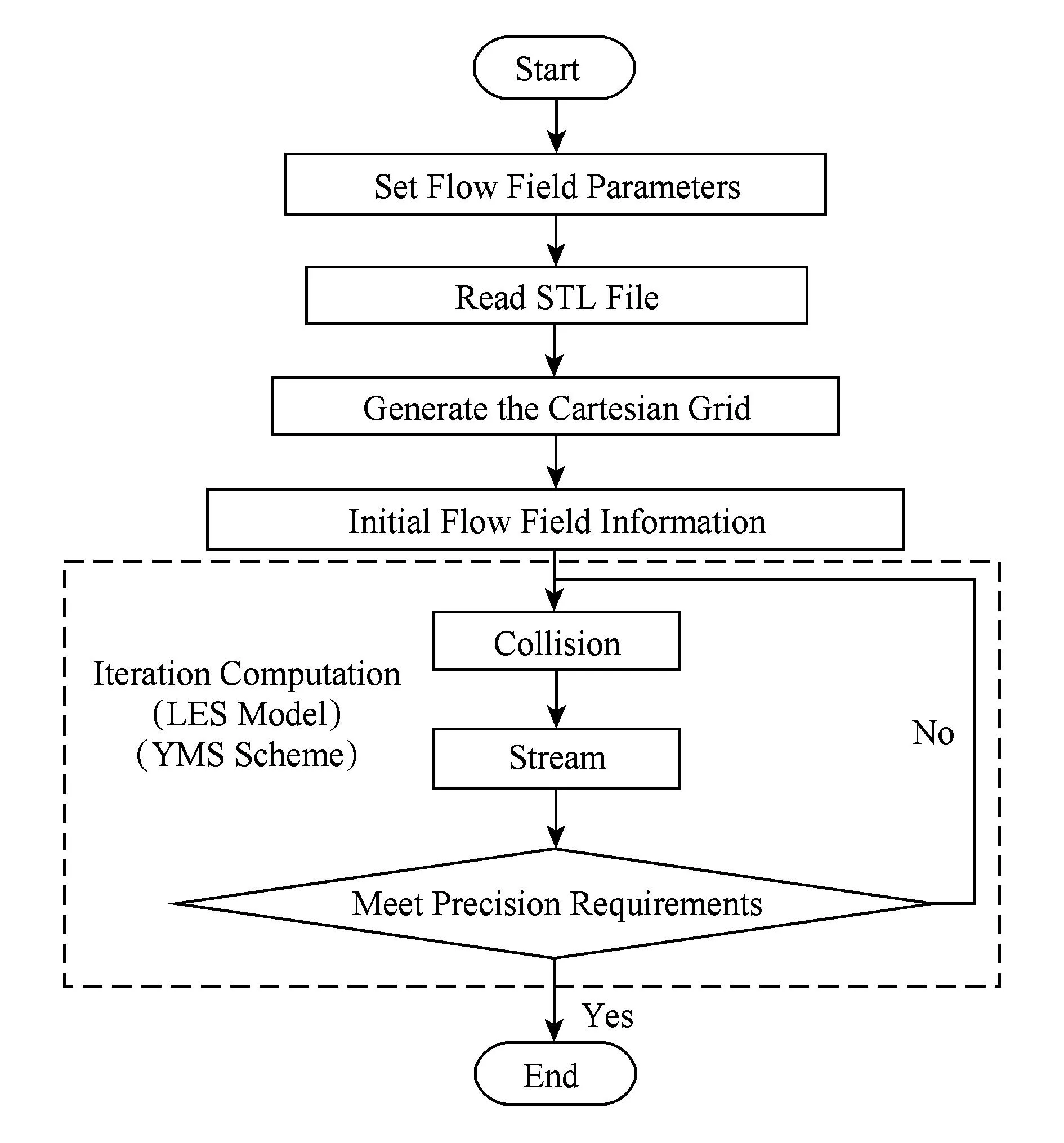
Fig. 3　Flowchart of MRT-LBM.图3　MRT-LBM的计算流程图

本节将根据图3中的MRT-LBM计算流程图，从笛卡儿网格生成开始，逐步分析MRT-LBM的并行性，并提出基于MRT-LBM的并行算法.MRT-LBM的求解基本流程主要包括3个部分：网格生成、流场信息初始化和迭代计算.下面我们将分别对这3部分进行并行性分析.

2.1网格生成部分的并行

MRT-LBM使用的是统一尺度的笛卡儿网格，如图4所示.笛卡儿网格的并行生成比较容易实现，其主要的难点在于从计算负载均衡的角度出发如何划分网格和网格点类型(包括流体网格点、边界网格点和几何体内部网格点)的判断.

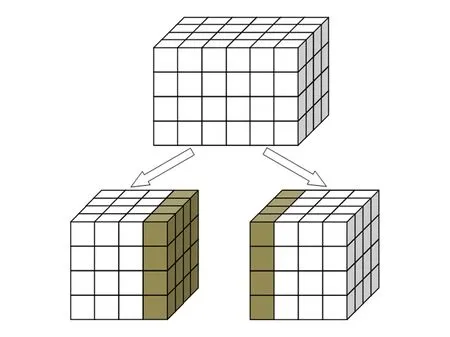
Fig. 4　Schema of three-dimensional grid parallel partition.图4　三维网格并行划分示意图

首先我们给出在三维情况下，网格生成的3个主要步骤：

Step1. 根据流场范围和网格尺寸Δx，生成1个初始的三维笛卡儿网格，每个网格点的信息包括：网格点的坐标值、图1中19个速度方向的邻居编号.

Step2. 根据复杂几何的STL文件格式，判断笛卡儿网格点在几何体的内外，一般采用射线法进行判断，具体判断算法可见文献[17].判断完成后需要标记网格点的类型：流场内网格点(fluid)、几何体内部网格点(solid).

Step3. 与几何体相邻的流场内网格点标记为边界网格点(boundary)，同时根据式(11)计算边界网格点沿着19个速度方向到几何体边界的距离值q.

根据Step1～Step3，并结合MRT-LBM的碰撞迁移过程(式(6)(7))和分布式集群的特点，网格生成部分进行并行操作步骤如下：

Step1. 根据计算进程数np，将流场范围均等分成np份，记录每一份的流场范围[(xi,min,yi,min,zi,min),(xi,max,yi,max,zi,max)](i=1,2,…,np).

Step2. 如图4所示，为了方便MRT-LBM的计算，在流场范围均匀划分时需要预留1块缓冲区，即每个计算进程负责的流场范围应该为[(xi,min-Δx,yi,min-Δx,zi,min-Δx),(xi,max+Δx,yi,max+Δx,zi,max+Δx)](i=1,2,…,np).

Step3.每个计算进程根据各自负责的流场范围，根据并行操作Step1～Step3各自独立生成MRT-LBM所需的计算网格.

从并行操作Step1～Step3中可以看出，每个计算进程在理论上分配的网格总数是一致的，且每个进程各自独立进行网格生成，无需通信，这样并行划分的网格生成的好处是能够被后续的MRT-LBM计算直接使用，且每个进程的网格数基本一致，具有较好的负载均衡.

2.2流场信息初始化部分的并行

笛卡儿网格生成后，需要进行的是网格点上流场信息的初始化，包括：宏观量(密度、速度、压力)的初始化和微观量(粒子分布函数)的初始化.宏观量的初始化主要是根据初始的宏观条件进行赋值，而微观量需要根据已赋值的宏观量通过平衡态分布函数进行计算获得.流场信息初始化的过程都是在每个网格点上独立进行，相邻网格点间无需通信.这里采用2.1节中的已经划分后的网格(每个MPI进行对应1个网格区域)，每个MPI计算进程内部都可以执行如下步骤：

Step1. 根据网格点的类型和初始的宏观条件给每个网格点赋初始宏观量的值.

Step2. 根据网格点上的初始宏观量,计算每个网格点上微观量的值.

由于2.1节中预留的缓冲区不用于计算，仅用于MPI的通信操作，所以在流场信息初始化时不需要涉及到该缓冲区.此外，根据2.1节已经完成了并行任务划分，本部分的计算操作仅需要对每个对应的MPI计算进程执行初始化，无需MPI通信.由于每个MPI进程的网格数基本一致，因此初始化部分是满足负载基本均衡，且具有良好的可扩展性和执行效率.

2.3迭代计算部分的并行

这部分是MRT-LBM计算的核心部分，迭代的每一次计算都包括碰撞过程(如式(6)所示)和迁移过程(如式(7)所示)，且在碰撞过程中还引入了大涡模拟湍流模型(如式(8)所示)，在迁移过程中需要使用曲面边界YMS插值格式(如式(10)所示).在给出具体的并行步骤前，我们先对涉及2.1节中缓冲区部分的MPI通信方式进行研究.由于在三维情况下的通信与二维情况的通信类似，为了便于描述，本文给出在二维情况下的一维网格划分和二维网格划分的通信模型，如图5所示：

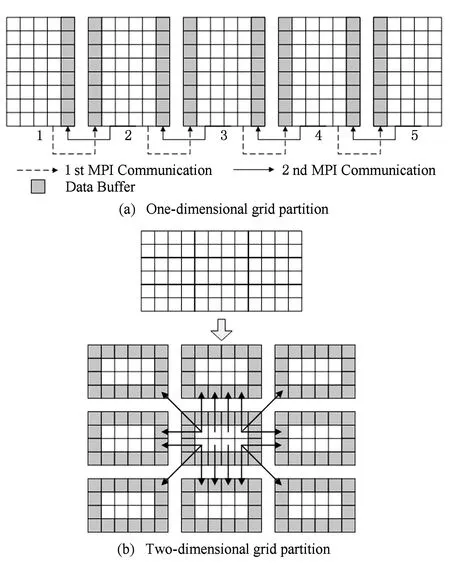
Fig. 5　Data transmission between processes.图5　进程间数据传递图

在图5中灰色部分为2.1节中所提的缓冲区部分，它只用于接收相邻网格块的数据.从图5(a)可以看出，一维网格划分情况的MPI数据传递相对简单，即相邻的MPI进程分别进行1次数据的传递与接收，如果采用非阻塞MPI通信仅需要2次MPI通信就能进行1次MRT-LBM的迭代计算.在图5(b)中，二维网格划分的MPI通信较为复杂，通信的次数也更多，但是该划分下的MPI通信与D2Q9离散速度模型是一致的.图5中的2种网格划分的进程间数据传递都反映出MRT-LBM仅需要局部通信，无需全局通信.而二维网格划分与一维网格划分相比，在同样的问题计算规模下，二维网格划分能够划分更多的网格块，可以扩大同一个计算问题下所能使用的计算核数.

类似地，针对三维问题中的D3Q19离散速度模型的MPI通信模型，也包括一维、二维和三维网格划分，每种划分都仅需局部通信.随着划分维数的增加，MPI通信的复杂程度也增加，但是所能划分的网格块越多，能够使用更多的计算核求解同一个问题，并加快求解速度.

结合图5中的MPI进程数据传递图和2.1节、2.2节中的并行内容，迭代计算部分的并行步骤(每个计算进程)如下：

Step1. 按照类似于图5中的进程间数据传递图，建立进程间MPI通信的编号数组，为后续的传递做准备；

Step2. 在除缓冲区和solid以外的网格点中，根据式(8)计算引入大涡模拟湍流模型的松弛参数s9和s13；

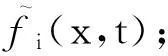
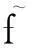
Step5. 根据式(7)进行fluid网格点的迁移，同时根据迁移后的值计算fluid网格点宏观量的值；

Step6. 根据式(10)进行边界网格点的迁移和计算宏观量的值；

Step7. 判断是否满足退出条件，如不满足则返回Step2继续计算，否则计算结束，输出计算结果.

迭代计算在MRT-LBM的整个求解过程中所占比重最大，也最耗时.上述的并行算法仅需要在相邻进程间进行通信，无需全局通信，具有良好的可扩展性，能够提高MRT-LBM在分布式集群上的执行效率，显著缩短计算时间.在流场信息初始化和迭代计算部分，直接使用了并行网格生成部分得到的计算网格，每个进程负责的网格数量保持一致，网格量负载均衡，但是由于在迭代计算中存在部分进程中的solid网格点不参与计算，可能会对迭代计算网格量的负载均衡产生一些影响，但是由于该部分网格点在总体网格量上所占比例不高，所以对整个MRT-LBM并行算法的可扩展性影响不明显.

3数值实验

本节将针对第2节中提出的MRT-LBM高可扩展并行算法，在国产神威蓝光超级计算机上进行详细的并行测试分析.

3.1测试环境

神威蓝光超级计算机是国内首个全部采用国产中央处理器(CPU)和系统软件构建的千万亿次计算机系统.其中计算节点共8 704个，每个节点采用的是具有自主知识产权的申威1 600(SW1600)处理器，每个处理器有16核、主频1.0GHz，神威总计算核达到130 000核以上，系统峰值为1070.16TFlops，测试性能为795.9TFlops.计算节点的内存为16GB，系统内存容量为170TB，外存容量为2PB.神威蓝光采用了胖树结构的互联网络，节点间采用了来自Mellanox的QDRInfiniband网络，其传输速度高达40Gbps.操作系统为国产“神威睿思”并行操作系统.

3.2测试结果

本文的测试用例选取为三维圆球绕流流动问题.测试主要分为3个部分：MRT-LBM高可扩展并行算法的数值稳定性和精度测试、固定问题的计算规模的并行效率测试和固定单个进程计算规模的并行效率测试.固定问题的计算规模并行测试的计算网格量分别选取3亿、6亿、13亿、26亿、52亿和100亿这6种固定规模(分别记为固定规模1～6).固定单个进程计算规模的并行效率测试保证每个进程中的计算网格量为2 000.测试的最大核数为130 000.

首先对MRT-LBM高可扩展并行算法的数值稳定性和精度进行测试分析.在三维圆球绕流问题的实验中，选取来流的马赫数Ma=0.2，雷诺数Re取值范围是10～1 000，计算的圆球阻力系数cd随雷诺数Re变化曲线见图6所示.从图6可以看出，MRT-LBM并行算法的计算结果与经验公式的结果基本符合，验证了MRT-LBM并行算法的数值稳定性和精度.

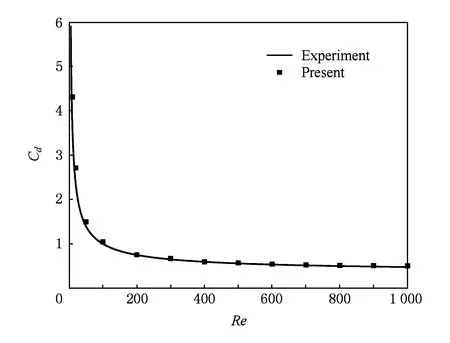
Fig. 6　Drag coefficient at variable Re.图6　阻力系数随Re变化曲线

接下来进行MRT-LBM高可扩展并行算法性能方面测试.根据图6中的结果，在接下来的三维圆球绕流问题的测试计算中，Re取值固定为1 000，Ma取值依然为0.2.

首先我们给出固定问题的计算规模的并行效率测试结果和分析.由于固定规模1～6计算网格量从几亿到百亿，问题的计算规模较大，考虑到神威蓝光超级计算机单个计算核心所能占用的内存资源不到1 GB，且随着计算问题规模的不断扩大，所需要使用的内存资源也越大，为了能够更好地进行加速比和效率的分析，所以本文中对固定规模1～6中所采用的最小计算核数为325核，且随着网格规模的增大，最小计算核数也不断增大，而本文所采用的最大测试核数统一为130 000核，测试所采用的MRT-LBM的迭代步骤统一设为100步.

图7和图8分别给出了固定规模1～6的加速比和并行效率.从图7可以看出，本文所提的并行算法加速比将随着计算规模的增大而不断增大，且在13万核时具有良好的加速比.从图8可以看出，随着计算问题的规模增大，其计算效率越接近理论值.

Fig. 7　The speedup of different fixed scales.图7　固定规模1～6的加速比

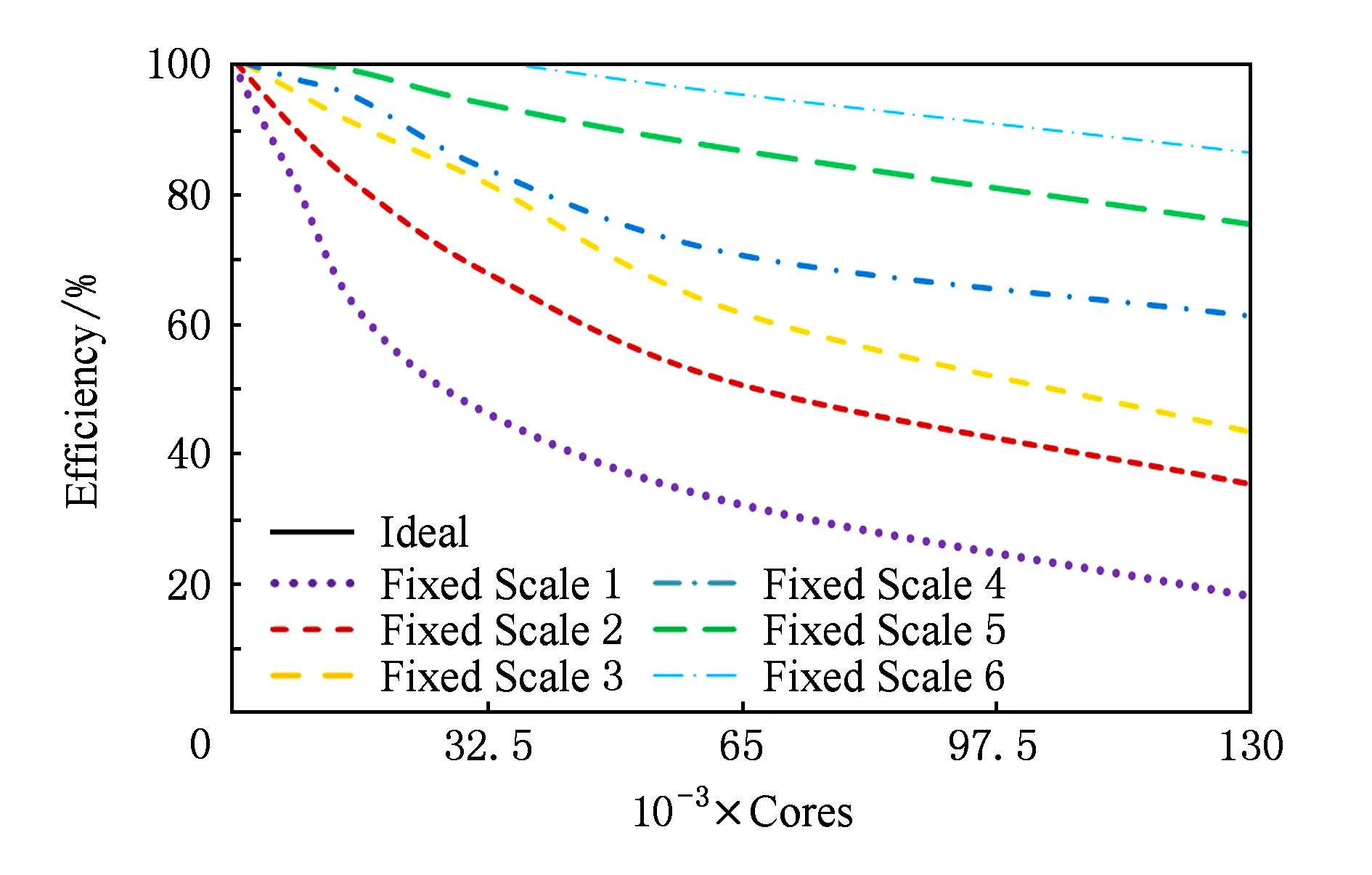
Fig. 8　The parallel efficiency of different fixed scales.图8　固定规模1～6的并行效率

下面进一步分析MRT-LBM并行算法的并行性能.考虑MRT-LBM并行算法中核心部分是迭代计算，在迭代计算中分为碰撞过程(见式(6))和迁移过程(见式(7)).根据MRT-LBM的计算流程如图3所示，迭代计算在整个计算中所占比例最大，且随着迭代次数的不断增加，整个计算时间基本就是MRT-LBM的迭代计算时间.这里我们针对固定规模5的情况，分析在使用8 125～130 000计算核时MRT-LBM迭代计算(含流场信息初始化)中MPI通信时间和计算时间的关系.这里我们将MRT-LBM的迭代计算时间记为TIter，MPI通信时间记为TComm，MPI进程的计算时间记为TComp，那么TIter=TComp+TComm.

图9给出了在固定规模5的情况下MPI通信和计算2部分分别在MRT-LBM迭代计算时间中所占的比例(计算核数是按照2的倍数增加)，其中通信占比为TCommTIter，计算占比为TCompTIter.图10和图11分别给出了对固定规模5计算中的MPI通信时间TComm和计算时间TComp.从图10和图11可以看出，随着计算核数的增加，迭代计算中的MPI进程的计算时间TComp几乎线性减少;而MPI通信时间TComm并没有显著增加，而是在同一个量级上缓慢变化.MPI通信时间TComm的稳定主要是由于MRT-LBM中仅需要局部通信，且在同一计算规模下每个MPI进程间的数据传递与接收量是一致的.因此图10和图11可以反映出图9中的不同计算核下的时间占比，即随着计算核数的成倍增加，计算的比重缓慢地不断减少，而通信的比重缓慢增加.因此MRT-LBM并行算法的整体加速比随着迭代计算中的MPI进程的计算时间TComp占比的提高而不断增大，但由于存在稳定在一定量级上的MPI通信时间TComm，因此并行算法的总体加速比只能无限接近于线性加速比.

Fig. 9　The percentages of communication time and computation time among iterative computation in the fifth fixed-scale.图9　固定规模5迭代计算中通信与计算部分的占比

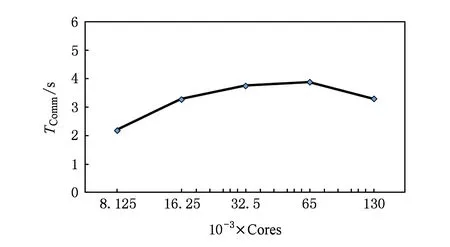
Fig. 10　The MPI communication time in the fifth fixed-scale.图10　固定规模5中不同计算核数下的MPI通信时间

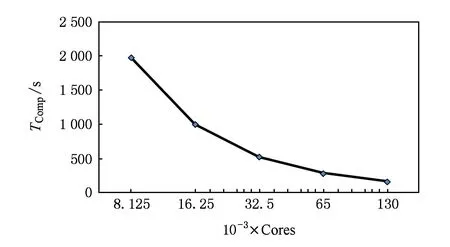
Fig. 11　The iteration computation time in the fifth fixed-scale.图11　固定规模5中不同计算核数下的迭代计算时间

结合图7～11可以看出，MRT-LBM并行算法具有良好的可扩展性，且在使用具有超大规模的高性能计算机时，只有当问题的计算规模足够大时才能更好地发挥机器的高性能.

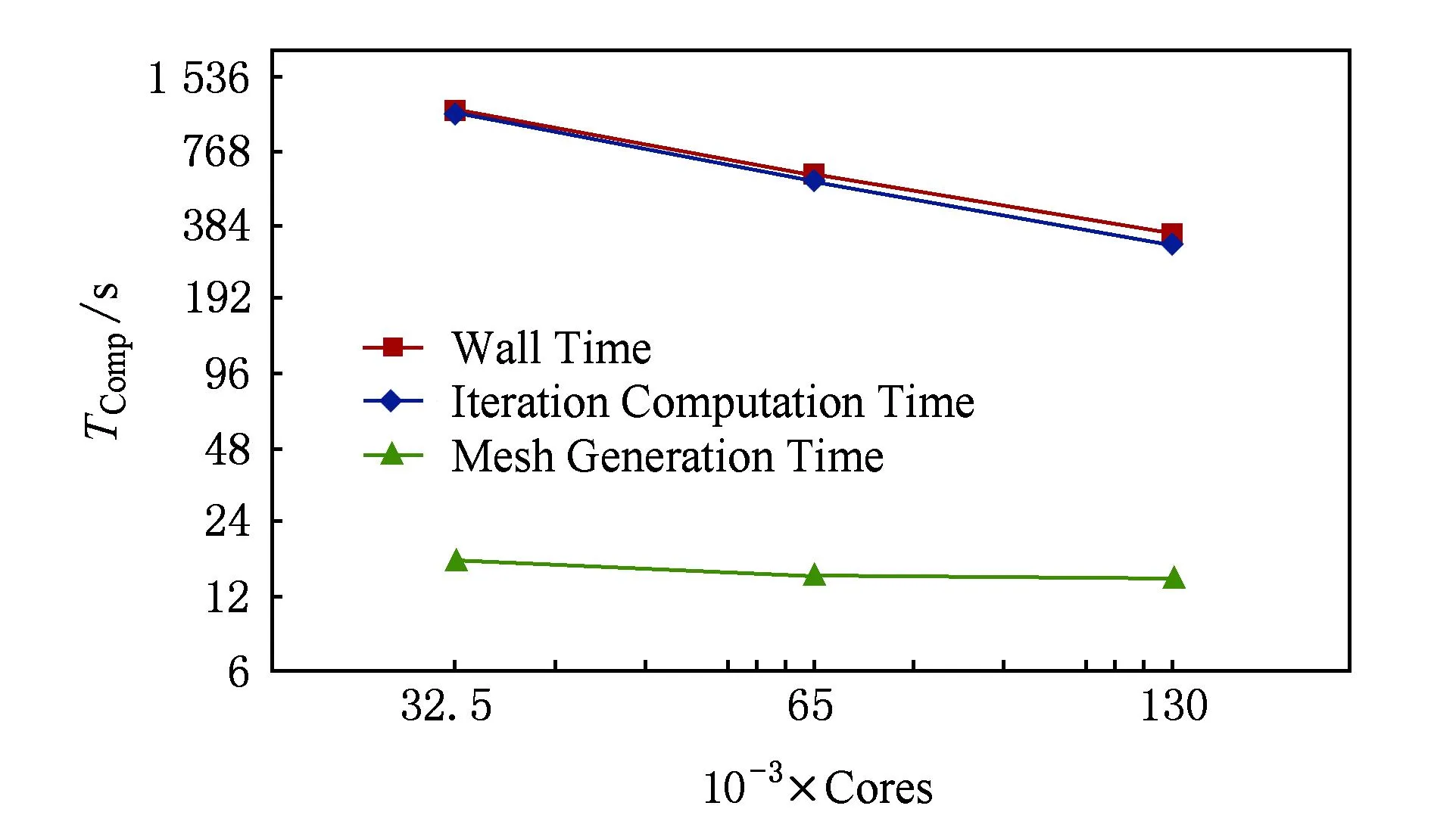
Fig. 12　Three kinds of computation time of the sixth fixed-scale changed with cores.图12　固定规模6中不同部分随核数变化的计算时间

为了进一步分析MRT-LBM并行算法的性能，接下来我们给出在固定规模6的计算情况，如图12所示.由于固定规模6的计算网格达到了百亿，所以考虑到内存的限制因数，测试的计算核数从32 500取到130 000，并给出了MRT-LBM并行算法中各部分(包括总计算时间、含流场信息初始化的迭代计算时间和网格生成时间)随着计算核数增加而计算时间变化的曲线.

从图12可以看出，总计算时间和迭代计算时间随着核数的增加而近似线性减少.但是网格生成计算时间却并没有显著减少，而是基本稳定在同一时间上，其主要原因是由于在进行网格类型判断和边界距离计算时(2.1节中的Step2和Step3)，因部分进程中不含边界网格点，导致网格生成时网格类型判断计算的负载不均衡，所以当计算核数达到临界值时并行网格生成时间几乎保持不变.但是这样的网格并行生成算法能够与MRT-LBM迭代计算相互融合，而无需重新再次划分计算区域，节省了再次划分网格块的时间，且MRT-LBM并行算法中网格生成仅是前处理的部分，所花费的时间与迭代计算的时间相差巨大，如图12所示，因此本文采用的并行网格生成算法对程序的整体并行效率并没有产生明显影响.

下面我们进一步分析MRT-LBM并行算法在固定单个进程计算规模的并行效率.在固定每个MPI进程的计算网格量为2500的前提下，计算核数从10 000核线性增加到130 000核，给出随着核数增加和网格量增大的情况下MRT-LBM并行算法的总计算时间、迭代计算时间和网格生成计算时间.如图13、图14所示，给出了在MRT-LBM的迭代计算中MPI通信和MPI进程的计算时间占比.

Fig. 13　Three kinds of computation time of computation scale increased with cores.图13　计算规模随核数增大的各部分计算时间

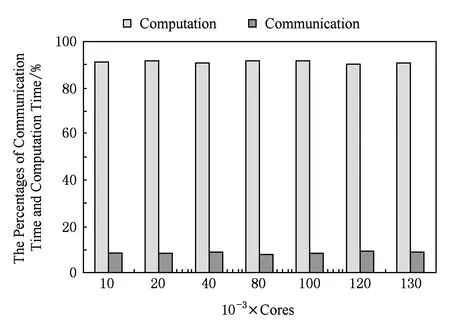
Fig. 14　The percentages of communication time and computation time among iterative computation.图14　迭代计算中通信与计算部分的占比

从图13可以看出，随着核数的增加和计算规模的增大，网格生成的时间、迭代计算时间和总时间几乎稳定在一个量级上.而从图14可以看出，由于每个MPI进程间的数据传递与接收量是一致的，且是局部网格块间进行通信，所以MPI通信的时间所在MRT-LBM迭代计算中的占比是几乎保持不变的，同时由于计算网格量的一致性，所以计算时间的占比也是几乎不变的.因此MRT-LBM并行算法在固定单个进程计算规模时仍然具有良好的可扩展性.

综合以上测试结果及分析，MRT-LBM高可扩展并行算法在13万核的量级上依然能够保持良好的数值稳定性、精度和加速比，且通信时间无明显增加，具有良好的可扩展性.

4结束语

在三维复杂流动的大规模数值模拟中，本文针对MRT-LBM具有边界处理简单、并行性好等特点，结合大涡模拟湍流模型、曲面边界插值格式、笛卡儿网格生成，详细分析了MRT-LBM算法的并行性，并给出了基于D3Q19离散速度模型的适合于大规模分布式集群的MRT-LBM高可扩展并行算法.该并行算法也同样适用于基于D3Q15和D3Q27离散速度模型的MRT-LBM.通过在国产神威蓝光超级计算机上的并行测试，验证了本文所提的MRT-LBM并行算法具有良好的数值稳定性和精度、并具有良好的可扩展性，在13万计算核上仍能够获得80%以上的并行效率.

MRT-LBM并行算法有望在千万亿次计算机上精确模拟三维实际流动问题中的湍流现象，为湍流的理论研究和发展提供相关帮助.目前，我们还将从网格技术角度出发，研究多块多重笛卡儿网格的自适应MRT-LBM并行算法.

参考文献

[1]Lallemand P, Luo L. Theory of the lattice Boltzmann method: Dispersion, disspation, isotropy, Galilean invariance and stability[J]. Physical Review E, 2000, 61(6): 6546-6562

[2]Succi S. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond[M]. Oxford, UK: Oxford University Press, 2001

[3]Aidum C K, Clausen J R. Lattice-Boltzmann method for complex flows[J]. Annual Review of Fluid Mechanics, 2010, 42(1): 439-472

[4]Freitas R K, Henze A, Meinke M, et al. Analysis of lattice-Boltzmann methods for internal flows[J]. Computers & Fluids, 2011, 47(1): 115-21

[5]Qian Yuehong, D’Humières D, Lallemand P. Lattice BGK models for Navier-Stokes equation[J]. Europhysics Letters, 1992, 17(6): 479-484

[6]Luo Lishi, Liao Wei, Chen Xingwang, et al. Numerics of the lattice Boltzmann method: Effects of collision models on the lattice Boltzmann simulations[J]. Physical Review E, 2011, 83(5): 056710

[7]D’Humières D, Ginzburg I, Krafczyk M, et al. Multiple-relaxation-time lattice Boltzmann models in three dimensions[J]. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 2002, 360(1792): 437-451

[8]Shan Xiaowen, Chen Hudong. A general multiple-relaxation-time Boltzmann collision model[J]. International Journal of Modern Physics C, 2011, 18(4): 635-643

[9]Tosi F, Ubertini S, Succi S, et al. Optimization strategies for the entropic lattice Boltzmann method[J]. Journal of Scientific Computing, 2006, 30(3): 368-387

[10]Yu Huidan, Luo Lishi, Girimaji S S. LES of turbulent square jet flow using an MRT lattice Boltzmann model[J]. Computers & Fluids, 2006, 35(1): 957-965

[11]Krafczyk M, Tolke J, Luo Lishi. Large-eddy simulations with a multiple-relaxation-time LBE model[J]. International Journal Modern Physics B, 2003, 17(1): 33-39

[12]Menon S, Soo J H. Simulation of vortex dynamics in three-dimensional synthetic and free jets using the large-eddy lattice Boltzmann method[J]. Journal of Turbulence, 2004, 5(5): 032

[13]Jahanshaloo L, Pouryazdanpanah E, Che Sidik N A. A Review on the Application of the Lattice Boltzmann Method for Turbulent Flow Simulation[J]. Numerical Heat Transfer Applications, 2013, 64(11): 938-953

[14]Li Leisheng, Wang Chaowei, Ma Zhitao, et al. PetaPar: A scalable and fault tolerant petascal free mesh simulation system[J]. Journal of Computer Research and Development, 2015, 52(4): 823-832 (in Chinese)(黎雷生, 王朝尉, 马志涛, 等. 千万亿次可扩展可容错自由网格数值模拟系统[J]. 计算机研究与发展, 2015, 52(4): 823-832)

[15]Hou S, Sterling J, Chen S, et al. A lattice Boltzmann subgrid model for high Reynolds number flows[J]. Pattern Formation and Lattice Gas Automata, 1996, 6(1): 151-166

[16]Yu Dazhi, Mei Renwei, Shyy Wei. A unified boundary treatment in lattice Boltzmann method[C]Proc of the 41st Aerospace Sciences Meeting and Exhibit. Reston, VA: AIAA, 2003: 0953

[17]Uzgoren E, Sim J, Shyy W. Marker-based, 3-D adaptive Cartesian grid method for multiphase flow around irregular geometries[J]. Communations in Computational Physics, 2009, 5(1): 1-41

Liu Zhixiang, born in 1986. PhD. His research interests include parallel algorithm and high performance computing.

Fang Yong, born in 1964. Professor and PhD supervisor. His research interests include blind signal processing, communication signal processing, and adaptive information system (yfang@staff.shu.edu.cn).

Song Anping, born in 1966. PhD and associate professor. His research interests include parallel computing, medical image processing and big data processing (apsong@shu.edu.cn).

Xu Lei, born in 1987. PhD candidate. Student member of China Computer Federation. His research interests include parallel algorithm and high performance computing (leixushu@shu.edu.cn).

Wang Xiaowei, born in 1970. Master. His research interests include high performance computing and computer architecture (wxw@shu.edu.cn).

Zhou Liping, born in 1984. Master. Member of China Computer Federation. His research interests include parallel algorithm and high performance computing (lpzhou@shu.edu.cn).

Zhang Wu, born in 1957. Professor and PhD supervisor. Senior member of China Computer Federation. His research interests include parallel algorithm and high performance computing.

Large-Scale Scalable Parallel Computing Based on LBM with Multiple-Relaxation-Time Model

Liu Zhixiang1,2, Fang Yong1, Song Anping3, Xu Lei3, Wang Xiaowei2,3, Zhou Liping2,3, and Zhang Wu2,3

1(SchoolofCommunicationandInformationEngineering,ShanghaiUniversity,Shanghai200444)2(HighPerformanceComputingCenter,ShanghaiUniversity,Shanghai200444)3(SchoolofComputerEngineeringandScience,ShanghaiUniversity,Shanghai200444)

AbstractIn the large-scale numerical simulation of three-dimensional complex flows, the multiple-relaxation-time model (MRT) of lattice Boltzmann method (LBM) has better property of numerical stability than single-relaxation-time model. Based on the turbulence model of large eddy simulation (LES) and the interpolation scheme of surface boundary, three iteration calculations of grid generation, initialization of flow information and parallelism property are analyzed respectively under the discrete velocity model D3Q19. Distributed architecture and the communication between different compute nodes using message passing interface (MPI) are often used by current high performance computing clusters. By considering both the features of distributed clusters and the load balance of calculation and using MPI programming model, the grid generation, initialization of flow information and the parallel algorithm of iteration calculation suitable for large-scale distributed cluster are studied, respectively. The proposed parallel algorithm also can be suitable for D3Q15 discrete velocity model and D3Q27 discrete velocity model. Two different cases, solving problem with fixed total calculation and solving problem with fixed calculate amount in every computing cores, are considered in the process of numerical simulation. The performances of parallelism are analyzed for these two cases, respectively. Experimental results on Sunway Blue Light supercomputer show that the proposed parallel algorithm still has good speedup and scalability on the order of hundreds of thousands of computing cores.

Key wordslarge-scale parallel computing; scalability; load balance; lattice Boltzmann method (LBM); multiple-relaxation-time model; large eddy simulation

收稿日期：2014-12-30；修回日期：2015-05-05

基金项目：国家自然科学基金重大研究计划培育项目(91330116)

通信作者：张武(wzhang@shu.edu.cn)

中图法分类号TP301.6

This work was supported by the Major Program of the National Natural Science Foundation of China (91330116).