随机型双边混流装配线平衡问题的两阶段求解方法研究

段移庭， 苏　平， 郑晨鸣

(广东工业大学 机电工程学院, 广东 广州 510006)



随机型双边混流装配线平衡问题的两阶段求解方法研究

段移庭， 苏平， 郑晨鸣

(广东工业大学 机电工程学院, 广东 广州 510006)

摘要：为降低求解随机型双边混流装配线平衡问题的复杂性，提出了一种遗传算法与仿真分析相结合的两阶段求解方法。首先建立忽略装配线同一工作站组的两工作站之间作业先后顺序约束的随机型双边混流装配线平衡问题的简化数学模型，采用一种基于序列组合编码方式的遗传算法对简化模型进行求解，获取备选解；在此基础上，建立考虑所有约束条件的仿真模型，通过系统仿真分析与评价，从备选解中获得该问题的最优解(或次优解)。算例研究表明，所提出的两阶段求解方法，在获得满意解的同时，可以大幅度降低问题求解的复杂性。

关键词：双边装配线平衡； 随机； 混流； 遗传算法； 仿真

装配线平衡问题(assembly line balancing problem, ALBP)是求解装配线上作业元素在各工作站的分配方案，使装配线在满足作业先后顺序约束的同时，各工作站单件作业时间接近,且不超过生产节拍，达到装配线利用率最大。装配线的平衡质量直接影响生产效率、生产成本和产品质量[1-3]。根据装配线上作业人员的操作方位，装配线可分为单边装配线和双边装配线两大类。双边装配线主要用于满足大型产品(例如汽车、冰箱等)的装配需求，与传统的单边装配线相比，双边装配线具有能缩短装配线长度，减少产品的下线时间，降低工装、夹具及物料处理的成本等优点[4]。因此，双边装配线平衡问题(two-sided assembly line balancing problem, TALBP)的研究越来越得到学术界和企业界的关注。

文献[4]首次提出了双边装配线平衡问题(TALBP)。双边装配线平衡问题比单边装配线平衡问题要复杂，因为对于双边装配线，在将作业元素分配到各工作站时，需要考虑作业元素在装配线上的操作方位约束以及装配线两侧工作站组(装配线两侧相对的工作站)之间由于作业先后顺序约束所引起的不可避免的等待时间。随着国内外学术界对双边装配线平衡问题研究的不断深入，涌现出一些有关双边装配线平衡问题的建模与求解方法的研究成果。文献[5]提出一种基于工位编码的遗传算法来解决双边装配线平衡问题，但该方法不能搜索整个可行解空间，只能得到局部最优解。文献[6]针对装配任务的相关度及任务安排上的松弛度的平衡问题，釆用多个启发式算法，以提高任务之间的相关度和不同工作站任务之间的松弛度。文献[7]提出一种基于“序列组合”(作业序列和作业方位组合)编码方法的遗传算法，提高了可行解的搜索效率。上述研究成果均是针对单一品种双边装配线平衡问题进行的研究。为了适应市场需求的多样化，多种产品混流生产成为主要生产模式。为了解决多种产品混流生产的问题，文献[8]提出了双边混流装配线平衡的第一类问题，以工作站组数目、生产节拍、工作站数目最少为目标，构建了多目标函数，并对双边混流装配线平衡的多目标优化问题进行了研究。文献[9]针对双边混流装配线平衡问题的特点，提出了一种改进蚁群算法，得到了作业分配方案。文献[10]考虑了并发操作的情况，建立了具有并发操作约束条件的双边混流装配线数学模型，并给出了遗传算法求解过程。文献[8，10]均假定装配作业时间为常数，而在实际生产环境下，特别是以手工作业为主的装配线，作业时间具有随机性，文献[11]在考虑双边装配线平衡特点的前提下，提出了一种具有操作方位约束的任务优先分配的启发式算法，得到不同的平衡方案，取得了较好的效果，但该研究是针对单一品种装配线进行的。

文献[12]针对混合装配线存在的不确定性问题，基于数学模型对不确定性因素进行了分析，并采用eM-Plant建模，通过系统仿真研究不确定性因素对混合装配线平衡的影响；文献[13]考虑随机混流装配线的特点，提出了一种混合粒子群算法来求解随机混流装配线平衡问题；文献[14]提出了一种基于集束搜索的算法来解决随机型混流装配线平衡问题。

文献[12-14]均是针对单边混流装配线平衡所做的研究，目前针对随机型双边混流装配线平衡问题的研究成果很少，而在企业生产实际中，双边混流装配线平衡问题普遍存在，特别是作业时间的不确定性对双边混流装配线平衡的影响不容忽视，因此对于随机型双边混流装配线平衡问题(stochastic two-sided mixed-model assembly line balancing problem, STMALBP)的研究更具有实际意义和研究价值。

1STMALBP描述与数学建模

1.1STMALBP描述

双边装配线是指在装配线的左右两边都设有作业工作站的装配线，装配线左右两边相对的两个工作站成对称分布，这一对工作站称为工作站组(mated-station)，而同一工作站组中的两个工作站互称为对方的伴随工作站(companion)[4]，如图1所示，该双边装配线包含5个工作站组。

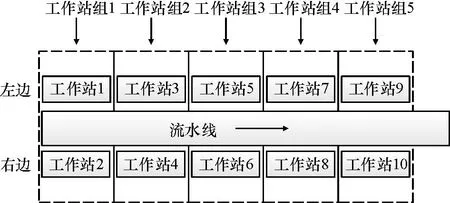
图1　双边装配线

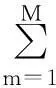
在双边装配线中，分配到同一工作站组的两个工作站中的作业元素可能由于作业先后顺序关系的约束，导致产生不可避免的“等待时间”，如图2所示。

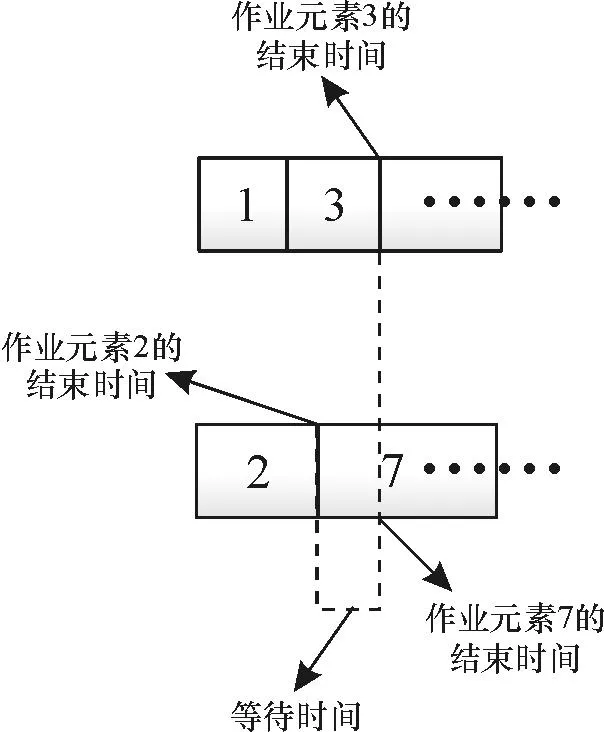
图2　“等待时间”描述

图2中，如果作业元素3是7的先行作业元素，装配线右边工作站在完成作业元素2后不能马上开始元素7的作业，而需要等元素3完成后才可以开始，从而产生了与作业元素3相关的“等待时间”。因此，双边装配线平衡问题与单边装配线平衡问题不同，在计算工作站作业时间时，不可以把分配到该工作站所有作业元素的作业时间直接相加，而需要把“等待时间”作为该工作站作业时间一部分，即工作站的作业时间等于所有作业元素时间与该工作站的“等待时间”之和。

在随机型双边混流装配线平衡问题中，由于不可避免的“等待时间”的存在，增加了问题的建模与求解的复杂性，为此本文提出一种将遗传算法和仿真分析相结合的两阶段求解方法，以简化问题的建模与求解过程。遗传算法具有良好的搜索能力和优化特性，能够有效寻找出装配线平衡问题的较优解。由于遗传算法是基于简化模型进行搜索的，搜索方向可以确定，但不能保证解的质量，因此，遗传算法所得到的解只能作为备选解。仿真方法是分析和求解随机性问题的有效方法，通过仿真分析，对备选解进行筛选，从而获得满足约束条件的随机型双边混流装配线平衡问题的最优解(或次优解)。

1.2不考虑等待时间的STMALBP数学建模

双边装配线平衡问题是将产品的作业元素分别分配到装配线左、右两边工作站中，在满足作业元素先后顺序关系约束和节拍要求的前提下，使得工作站组的数目最小。如前文所述，当考虑同一工作站组左右两个工作站之间作业元素先后顺序关系约束的情况时，可能产生不可避免的“等待时间”，增加了数学规划模型的复杂性，因此，暂时不考虑“等待时间”。

基于如下假设条件建立问题的简化数学规划模型：1)问题所有输入参数均为已知；2)各个作业元素作业时间tmi之间互相独立，各个工作站之间互不影响；3)混合排产生产的产品结构相似，工艺相近；4)不考虑并行操作和作业“等待时间”的情况。

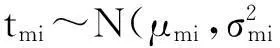
C 表示装配线节拍(指连续相同的两个产品的下线时间间隔)；

I 表示双边装配线上所有作业元素集合，I = {1, 2, …, i}；

P(i) 表示作业元素i的先行作业元素的集合；

AL、AR表示分别分配到双边装配线左边、右边的作业元素的集合，AL、AR∈I；

AE表示既可以分配到左边又可以分配到右边的作业元素的集合，AE∈I；

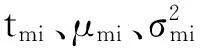
N 表示双边装配线上工作站组数目；

d(i) 表示作业元素的作业方位

(n, d) 表示工作站组n中的一对工作站，且(n, d1)和(n, d2)互为伴随工作站；

Wind表示分配到工作站(n, d)中的作业元素集合；

xind表示作业元素i分配到工作站组n、操作方位为d的工作站中，且当作业元素i被分配到工作站(n, d)时，xind的值为1，否则为0；

Tkm表示m型号产品被分配到工作站k中的作业元素的作业时间，Ikm表示m型号产品被分配到工作站k的作业元素集合；

xi为决策变量，为作业元素i所分配的工作站的序号。

当作业时间为随机变量时，会导致整个工作站的作业时间成为随机变量，理论上，在确定合理的节拍后，很难保证工作站内作业时间都满足节拍的要求；所以，对于作业时间随机变化性的装配线，工作站作业时间Tkm≤C(m=1,2,3…M)，只能以一定的概率α(0<α<1) 来满足节拍的要求，即

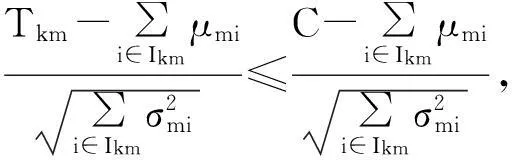
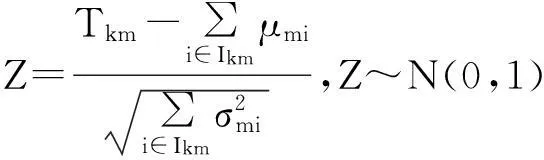
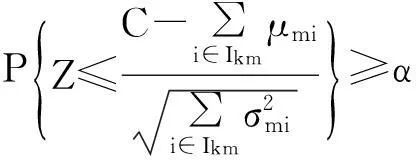
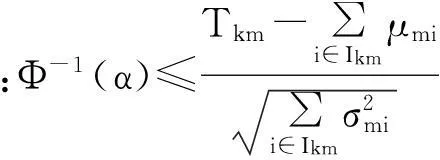
在随机型双边混流装配线平衡问题的第1阶段求解中，由于不考虑“等待时间”，在这种情况下，若仍然以给定的节拍C为工作站时间的约束条件，所求得的备选解可能会在考虑“等待时间”时，成为不可行解(即工作站时间超出节拍C)，为此，在问题的第一阶段求解中，引进一个适当的参数Δ，将节拍暂时调整为C'=C-Δ， STMALBP简化数学模型相关表达式如下。

F=min(N)。

(1)

(2)

(3)

∪Wind=I;

(4)

(5)

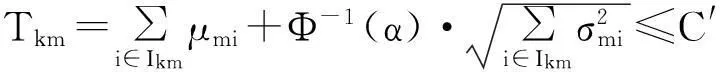
(6)

式(1)表示目标函数，以最小化工作站组数目为目标；式(2)表示作业先后顺序关系约束，在式(2)中，a∈P(i)，b∈I-P(i)；式(3)表示操作方位的约束；式(4)表示所有作业元素被分配到工作站；式(5)表示每个作业元素只能分配给一个工作站；式(6)表示各个工作站的作业时间小于调整节拍C'，其中m=1,2,3,…,M，对于任一分配到各个工作站的k的产品的所有作业元素而言，它们都必须在调整节拍内完成作业。

2STMALBP简化模型遗传算法求解

由于STMALBP问题的复杂性，本文采用两阶段求解方法。第1阶段采用遗传算法求解STMALBP简化模型。遗传算法求解装配线平衡问题主要有3种编码方式：基于作业序列号、基于工位号、基于序列组合的编码。在双边装配线平衡问题中，不仅要考虑作业元素分配的工作站，还要考虑该元素的作业方位。基于序列号的编码方式无法满足双边装配线平衡对作业元素操作方位的要求，而基于工位号的编码方式中需要对作业元素的装配顺序进行排序，增加了问题的复杂性。因此，基于序列组合的编码方式更适合双边装配线平衡问题。

2.1基于序列组合编码方式

在基于序列组合的编码方式中，染色体各个基因由两部分组成：作业元素的序列号和相应的作业方位[7]。即按照作业元素分配到工作站的先后顺序，将作业元素排成1列，染色体长度等于作业数，每个作业元素对应1个基因，其取值为作业元素i和其分配的方位d(d=L、R、E)的组合(i,d)。以P16问题[11]为例，一条染色体的编码形式如图3所示。

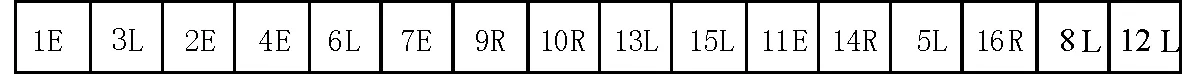
图3基于序列组合编码形式

Fig.3Sequence-based combined coding schemes

2.2解码

解码时，将染色体从左至右依次进行解码，具体过程如下。

1) 开启第1个工作站组n(n=1)，根据染色体第i个基因代码d的值，判断第i个基因位对应的作业元素的作业方位，并将作业元素i分配到相应工作站当中(d=R，即分配到相应位置的右边工作站；d=L，则分配到左边工作站；d=E则随机分配到任意一边)。

2) 计算当前位置工作站的所有作业元素的作业时间Tkm，判断当前工作站所有作业元素的作业时间是否小于或等于C'，如果满足要求(式(6))，分配到当前位置对应工作站。否则，开启下一个工作站组(n=n+1)，分配到对应的工作站中。如此重复前面两个步骤，直到染色体所有的基因解码完毕。同样，以P16为例[11]，如果给定节拍为19，图3所示的染色体解码的结果如图4所示。

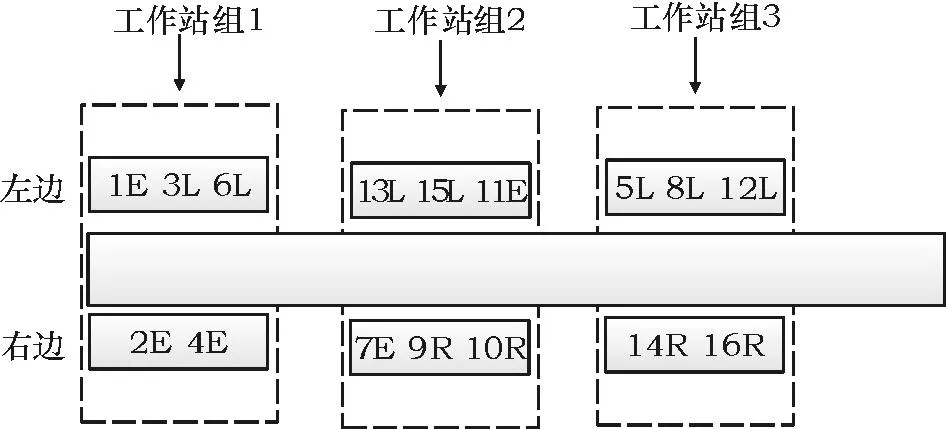
图4　染色体解码结果图

2.3初始化

在遗传算法中，染色体初始化的目的是生成一组可行染色体。采用遗传算法求解双边装配线平衡问题中，染色体初始化是在保证作业元素先后顺序的前提下，通过随机方法产生初始种群：可分配的作业元素和相对应的作业方位序列。具体步骤如下。

1) 在作业元素集I中，找出所有无前序元素或前序作业元素已分配完的作业元素，并且放到集合Y当中。

2) 从Y中随机选择一个作业元素i，并将其跟该元素i在装配线上的作业方位d(L,R,E)相组合，作为染色体的当前基因值(i,d)，例如，(2,R)。

3) 重复前面两个步骤，直到Y中所有作业元素都分配完成为止，即完成一条染色体的初始化。

4) 重复步骤(1)、(2)、(3)X次，可以得到X条可行染色体，X就是初始化种群的大小。

2.4适应度函数

装配线平衡问题的目的就是使平衡率最大化，因此把装配线的平衡率作为染色体的适应度函数(式(7))，Eval值越大，表明该染色体越优；采用轮盘赌选择操作，来进行选择和淘汰，即适应度值越大的染色体，被选择的概率越大。

(7)

2.5交叉和变异

1)交叉又称重组，是按较大的概率从群体中选择两个个体作为父代，通过交换两个父代的某些位上的基因，形成两个不同的子代个体。两点交叉是指在两个父代个体的染色体中设置两个交叉点，根据指定的交叉概率，交换两个交叉点之间的部分基因，图5为两点交叉示意图。

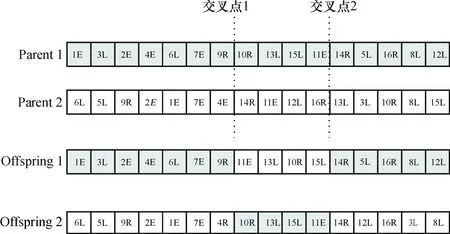
图5　两点交叉示意图

2)变异是将染色体中的某些基因进行互相交换，形成一个新的染色体，图6为变异操作示意图。

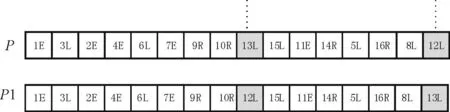
图6　变异操作示意图

2.6算法终止条件

通常，当最优个体的适应度和群体适应度不再上升时，或者当前进化代数达到预设的代数时，算法终止。本文令当前进化代数达到预设最大遗传代数(例如100代)时，遗传算法终止。

3考虑等待时间的STMALBP仿真方法

上一节已经完成了两阶段求解的第1步，本节将进行第2步求解，鉴于第1步的结果是在简化模型下完成求解的，该简化模型未考虑“等待时间”，因此本节通过eM-Plant软件建立考虑“等待时间”的仿真模型，对在简化模型下求解的备选结果进行仿真评价与分析，求得问题最终解。

在双边装配线中，由于“等待时间”的存在，因此不能把各个工作站中的作业元素时间之和作为工作站的作业时间，该等待时间关系可以通过下面的数学关系来表示，从而满足节拍要求。

stmi=max(tl,tr)；l, r ∈P(i), l∈AL, r∈AR。

(8)

stmi+tmi≤C，∀i∈I,m=1,2,3，…，M。

(9)

式(8)中stmi表示m型号产品作业元素i的开始操作时间，其中stmi为m型号产品在工作站(n,d1)中作业元素i的先行元素l的结束时间tl以及伴随工作站(n,d2)中作业元素i的先行元素r的结束时间tr之间的较大值；式(9)表示对于所有作业元素i都要在节拍内完成(采用一种基于“任务在工位上开始装配时间”的方法[15])。

eM-Plant软件是一个面向对象的图形化的建模和仿真软件，可以广泛应用于生产系统的仿真、优化[16]。通过eM-Plant建立仿真模型，在模型中把备选解中所有工作站作业时间相应的“等待时间”考虑进去，图7为考虑“等待时间”的随机型双边混流装配线的仿真模型示例图。

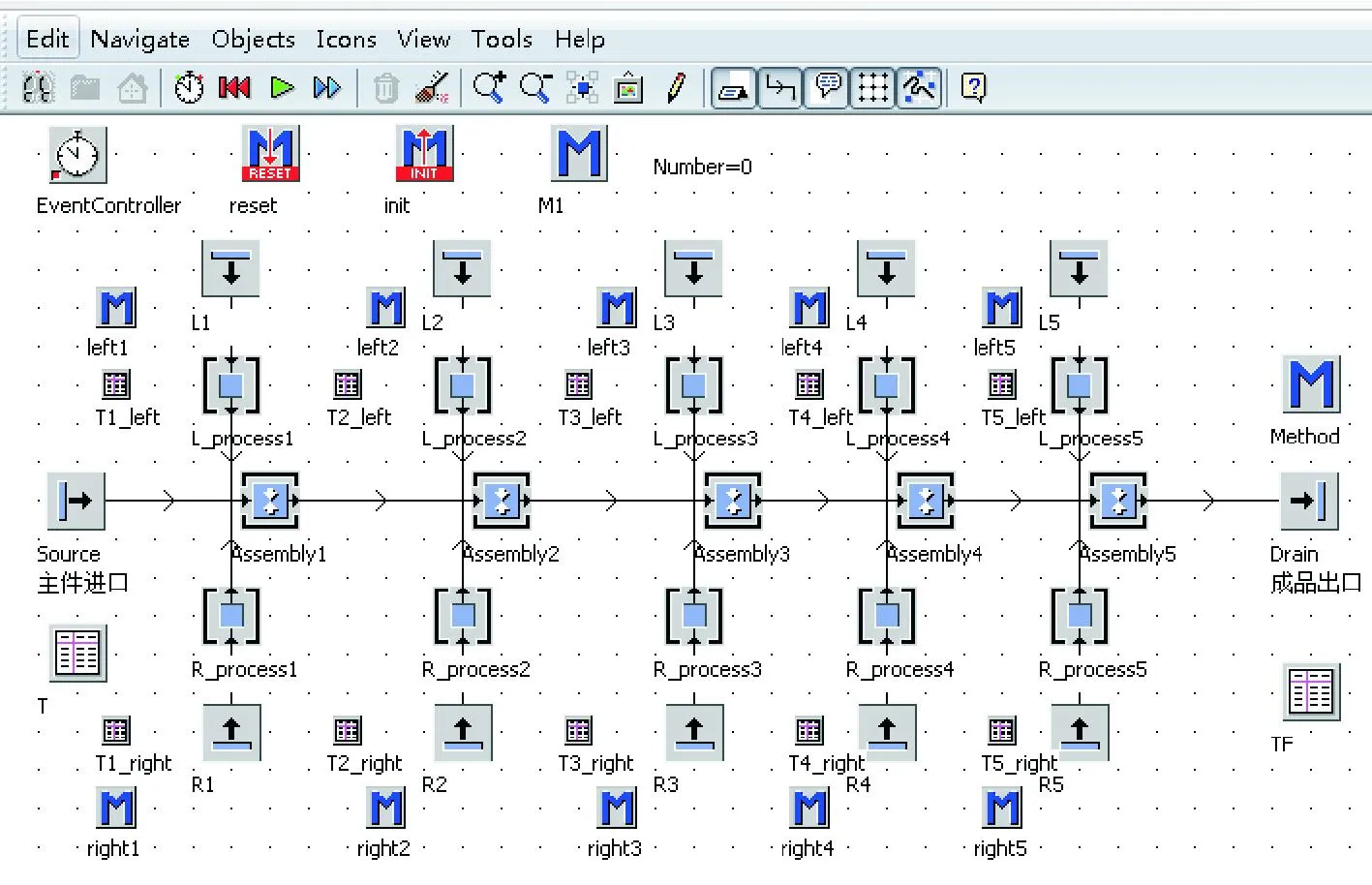
图7　考虑等待时间的STMALBP仿真模型示例图

4算例分析

以文献[10]中的实例问题进行求解分析，该实例是在某冰箱企业的一条双边装配线上，需要装配A、B、C、D 4种工艺相似的产品，其中箱体某个部分由20个作业元素组成，按照最小循环生产比例投产，设最小循环生产比例为6∶6∶5∶5，4种产品的综合作业先后顺序关系如图8所示。

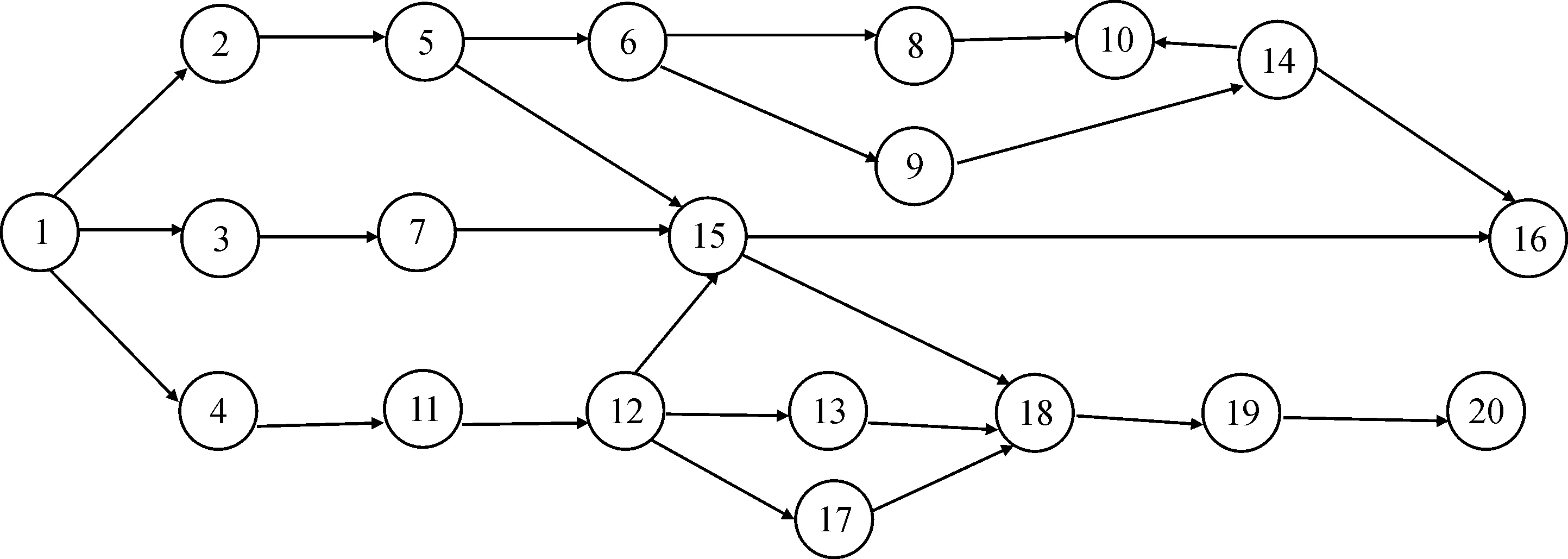
图8　4种产品混合作业先后顺序关系图

A、B、C、D 4种产品的不同作业元素的作业时间如表1所示。由于原问题没有考虑到作业时间的随机性，给出的是确定作业时间；对于一般熟练工而言，作业时间方差范围为1.2～2。因此，本文对参考文献中的作业时间作一些调整，取随机型模型中各个作业时间的均值为表1中各个作业时间，方差为1.5(时间单位为s)。

表1　4种产品作业时间表

鉴于遗传算法求解的是备选解，因此需要求得多组解，下面通过改变不同遗传代数来求一组(求解10次)备选解。在随机型模型中，预设概率与Φ-1(α)的取值有关，如果Φ-1(α)=1.280，则不超过节拍的概率为90%；如果Φ-1(α)=1.960，则不超过节拍的概率为97.5%。根据以上条件，采用前面的STMALBP简化模型和遗传算法在Matlab中来寻找一组较优解。算法输入参数为，预设种群大小X=50，交叉概率Pc=0.7，变异率Mu=0.1，输入不同的最大遗传代数(取50～100之间)，当节拍C=20，Δ=0.1×C=2，在Φ-1(α)=1.960时，求得结果如表2所示。

表2　一组较优分配结果

为了进一步从上述分配结果中筛选出最优解，通过eM-Plant软件对上述备选解进行建模仿真分析。在仿真模型中，考虑作业“等待时间”，对10组备选分配结果进行仿真，通过修改模型中的随机数流，多次运行(每组运行10次)，得到的各个备选方案的平均平衡率如表2所示。以第1个解为例，1{1L2E5L;3R4R11E}表示第1组工作站，工作站组1的左边分配的作业元素为：1、2、5，右边的作业元素为3、4、11。从表2中可以看出，当不考虑作业等待时，第1个解的平衡率79%最高，工作站组数目4也是最小，理论上为最优解。通过eM-Plant建模，加入“等待时间”之后运行结果如图9所示，第4个工作站组作业时间超过了节拍20，故而该解对应的分配方案淘汰。通过对所有的候选解进行多次仿真之后，各个备选解的平均平衡率统计结果如表2所示，比较各个备选解在仿真模型多次运行下的平均平衡率，可知最优解为第6个，该解对应的工作站组数目为5，平均平衡率为92.7%。

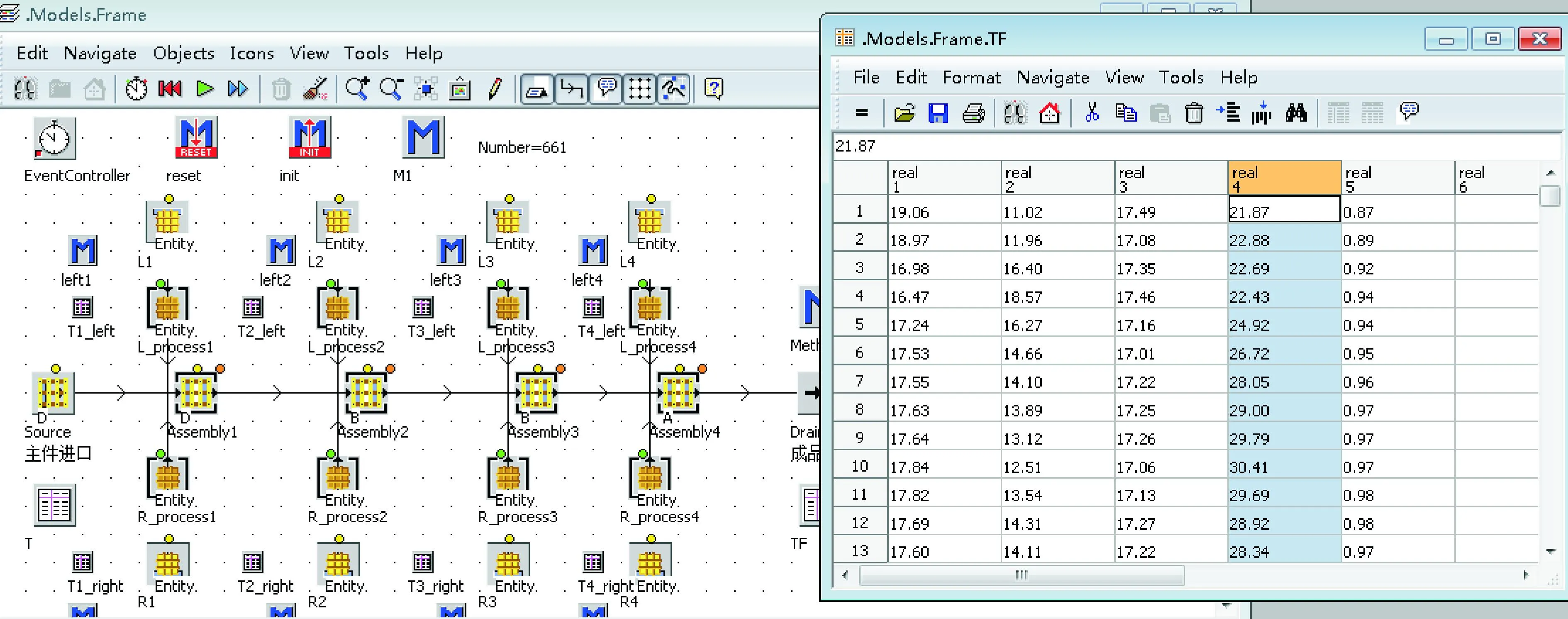
图9　仿真模型运行示例图

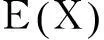
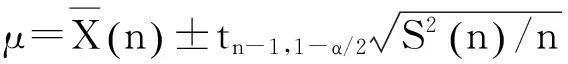
(10)

(11)

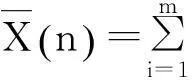
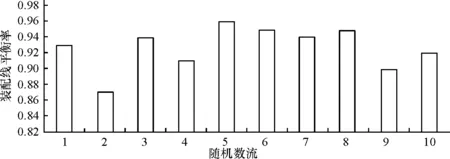
图10　不同随机数流下运行结果

验证所输出的数据是否以一定的置信度(90%)在式(10)、(11)所计算的置信区间内，通过计算，结果如表3所示，在α=0.1时，可以认为仿真模型输出结果以置信度为90%位于置信区间[0.891，0.963]上。

表3　仿真模型可信性验证表

通过以上实例表明，本文所提出的基于遗传算法和仿真分析相结合的两阶段求解方法能够有效解决随机型双边混流装配线第1类平衡问题。

5结论

本文针对双边混流装配线平衡问题，提出了基于遗传算法和仿真分析相结合的随机型双边混流装配线平衡问题的两阶段求解方法，并通过算例分析表明，该方法可以降低问题建模与求解的复杂性。本文只是对随机型双边混流装配线第1类平衡问题进行了研究，可以进一步研究第2类平衡问题；其次，在混流装配线中，往往不能以最小循环生产比例投产，还需要考虑投产排序给生产带来的影响，这些都将是后续研究的方向。

参考文献：

[1]SALVESON M. The assembly line balancing Problem[J]. Journal of Industrial Engineering, 1955, 6(3):18-25.

[2]陈心德，吴忠. 生产运营管理[M]. 北京：清华大学出版社，2005.

[3]ARMIN S, CHRISTIAN B. State-of-the-art exact and heuristic solution procedures for simple assembly line balancing[J]. European Journal of Operational Research, 2006, 168(6):666-693.

[4]BARTHOLDI J. Balancing two-sided assembly lines: a case study[J]. International Journal of Production Research, 1993, 31(10):2447-2461.

[5]KIM Y. Two-sided assembly line balancing: a genetic algorithm approach[J].Production Planning & Control, 2000, 11(1):44-45.

[6]LEE T O. Two-sided assembly line balancing to maximize work relatedness and slackness[J]. Computers & Industrial Engineering, 2001, 40(3):273-292.

[7]吴尔飞, 金烨,续爱民,等. 基于改进遗传算法的双边装配线平衡[J].计算机集成制造系统,2007, 13(2):268-274.

WU Erfei, JING Ye, XU Aimin, et al. Two-sided assembly line balancing based on modified genetic algorithm[J]. Computer Integrated Manufacturing Systems, 2007, 13(2):268-274.

[8]ÖZCAN U.Multiple-criteria decision-making in two-sided assembly line balancing: a goal programming and a fuzzy goal programming models[J]. Computers & Operations Research, 2009, 36(6): 1955-1965.

[9]陈建行, 张其松. 蚁群算法在装配线平衡问题中的应用[J]. 计算机时代, 2008(12):20-22.

CHEN Jianhang, ZHANG Qisong. Ant colony algorithm in the application of the assembly line balancing problem[J]. Computer Era, 2008(12):20-22.

[10]杨涛, 鲁建厦, 孔令革. 具有并发操作的双边装配线平衡问题研究[J]. 浙江工业大学学报, 2011, 39(4): 440-444.

YANG Tao, LU Jiansha, KONG Lingge. Study on balancing problem of two sided assembly line with concurrent operation[J]. Journal of Zhe Jiang University of Technology, 2011, 39(4): 440-444.

[11]宋林, 张则强, 程文明,等.随机型双边装配线平衡问题的一种启发式算法[J]. 工业工程, 2011, 14(4):129-134.

SONG Lin，ZHANG Zeqiang, CHEN Wenming, et al. Heuristic for two-sided stochastic assembly line balancing[J]. Industrial Engineering Journal, 2011, 14(4):129-134.

[12]于兆勤. 混合型装配线平衡问题的不确定性仿真研究[J]. 中国机械工程, 2008, 19(11): 1297-1302.

YU Zhaoqin. Simulation of uncertainty for mixed-model assembly line balancing problem[J].China Mechanical Engineering, 2008, 19(11): 1297-1302.

[13]张则强, 余庆良, 胡俊逸,等. 随机混流装配线平衡问题的一种混合粒子群算法[J]. 机械设计与研究, 2013, 29(2): 60-63.

ZHANG Zeqiang, YU Qingliang, HU Junyi, et al. Hybrid particle swarm optimization algorithm for balancing problem of stochastic mixed-model assembly line[J].Machine Design and Research, 2013, 29(2): 60-63.

[14]黄卫平, 张健, 周支立. 随机型混合模式装配线平衡问题的集束搜索算法[J]. 运筹与管理, 2010, 19(6): 20-26.

HUANG Weiping, ZHANG Jian, ZHOU Zhili. A beam search approach to stochastic mixed-model assembly line balancing problem[J]. Operations Research and Management Science, 2010, 19(6): 20-26.

[15]吴尔飞. 双边装配线平衡技术的研究[D]. 上海：2009, 上海交通大学.

WU Erfei. Research on balancing two-sided assembly line[D]. shanghai: Shanghai Jiao Tong University,2009.

[16]施於人. eM-Plant仿真技术教程[M]. 北京：科学出版社, 2009.

[17]肖田元，范文慧. 系统仿真导论[M]. 北京：清华大学出版社, 2010.

A Two-stage Method for Solving the Stochastic Two-sided Mixed-model Assembly Line Balancing Problem

DUAN Yiting, SU Ping, ZHENG Chenming

(School of Electro-mechanical Engineering, Guangdong University of Technology, Guangzhou 510006, China)

Abstract：To reduce the complexity of solving the stochastic two-sided mixed model assembly line balancing problem, a two-stage procedure of combining a genetic algorithm with simulation analysis is proposed. Firstly, a simplified mathematical programming model is formulated ignoring the constraint of precedence relation between the tasks assigned to the same mated-station, and a set of solutions is obtained by using a genetic algorithm based on a sequence combined encoding. Based on the set of solutions, a simulation model that takes all the constraints of the problem into account is developed. The optimal solution (or suboptimal solution) of the problem is obtained through simulation analysis and evaluation. The analysis of an illustrative example shows that the complexity of solving the problem can be greatly reduced and a satisfactory solution can be obtained with the proposed method.

Key words：two-sided assembly line balancing; stochastic; mixed-model; genetic algorithms; simulation

收稿日期：2015- 03- 06

作者简介：段移庭(1989-)，男，湖南省人，硕士研究生，主要研究方向为离散事件系统仿真、装配线平衡问题.

doi:10.3969/j.issn.1007- 7375.2016.02.020

中图分类号：TP205；TP301.6；N945.13

文献标志码：A

文章编号：1007-7375(2016)02- 0134- 09