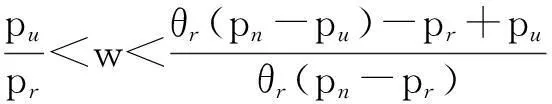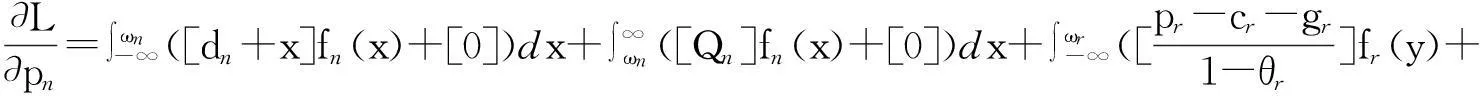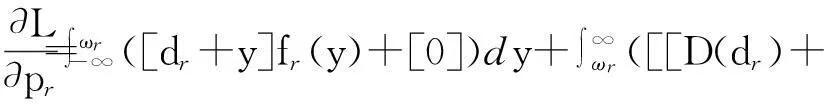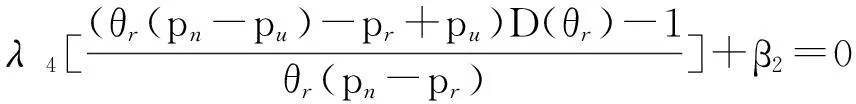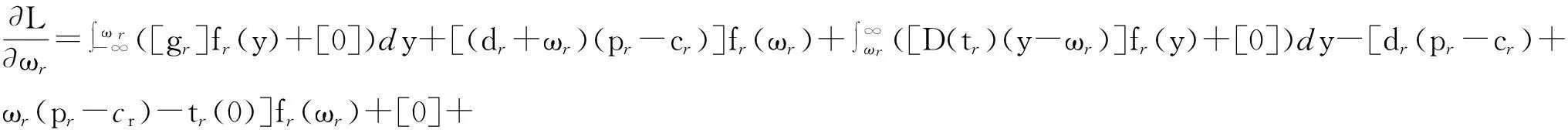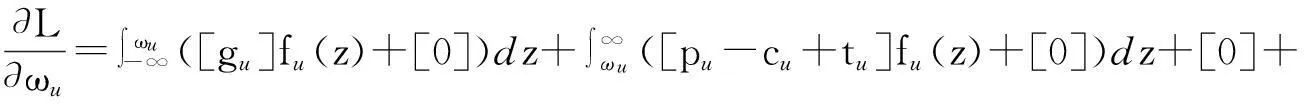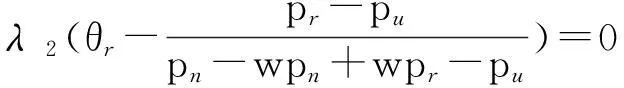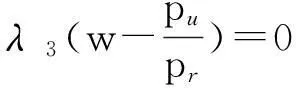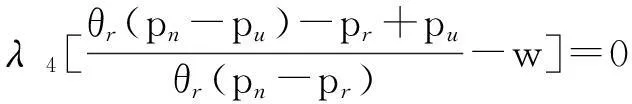质量差异和WTP差异下报废汽车资源化产品联合定价决策研究

蔡克元， 邹　晔， 王增强

(西南交通大学 交通运输与物流学院，四川 成都 610031)



质量差异和WTP差异下报废汽车资源化产品联合定价决策研究

蔡克元， 邹晔， 王增强

(西南交通大学 交通运输与物流学院，四川 成都 610031)

摘要：为使资源化产品定价有序合理化，以单一制造商为研究对象，在需求不确定环境下，对汽车零部件新产品、再制造产品和再利用产品的联合定价决策进行了研究。首先基于新产品、再制造产品和再利用产品三者之间的质量差异和支付意愿(WTP)差异，运用效用理论构建产品需求函数，然后以此为基础构建产品联合定价模型，最后通过数值仿真对模型进行求解。结果表明，随着再利用产品质量的提高，新产品价格和再制造产品价格总体呈下降趋势，再利用产品价格总体呈上升趋势，3种产品的产量总体呈下降趋势，制造商利润总体呈上升趋势。

关键词：质量差异； 支付意愿(WTP)差异； 联合定价； 报废汽车

报废汽车资源化是以报废汽车零部件为对象，在规范的市场运作下，通过现代先进技术、工艺和手段，尽可能充分挖掘其中蕴含的资源、能源及经济附加值等财富，使其转化为有用资源的过程[1]。报废汽车资源化的方法有再循环、再利用、再制造三种[2]。本文研究的资源化产品为再制造产品和再利用产品，二者的原料来源和特征如表1所示。本文假定市场上某汽车零部件制造商既生产零部件新产品，又回收拆解消费者手中的报废汽车，生产汽车零部件再制造产品和再利用产品，故论文研究的是，在需求不确定、3种产品质量不一以及消费者对3种产品的接受度不一的情形下，如何进行联合定价以实现制造商利润最大化及消费者效用最大化，该制造商运作过程如图1所示。

表1 汽车零部件资源化产品原料来源和特征

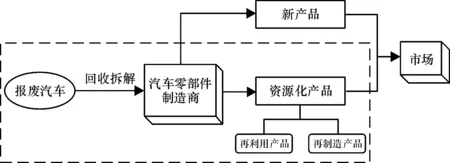
图1　 汽车零部件制造商运作过程图1

霍佳震等[3]构建了一个需求同时依赖于销售价格和库存水平，生产率和变质率均为常数，允许缺货且缺货量部分延迟订购的易变质品联合定价与生产控制模型。孙彩虹[4]在报童仅获知不确定需求的均值与方差的假设下，建立了Worst-case型的鲁棒联合定价、订货模型，并在适当的条件下给出了联合决策的闭环最优解。郭军华等[5]假设新产品质量与再制造产品质量相同，在需求不确定环境下，基于二者的WTP差异，对二者的联合定价决策进行了研究，并分析了消费者对再制造产品的认知程度对定产品定价、产量及制造商利润的影响。林欣怡等[6]在需求不确定环境下，以利润最大化为目标，研究了传统生产厂与再制造工厂主从博弈时的最优定价及产量，并将模型拓展至垂直纳什均衡和集成厂商的情形，最后对模型进行了仿真分析。李响等[7]以单一的再制造企业为研究对象，考虑适合再制造的量即产率为随机变量，并假设需求亦为随机变量，以利润最大化为目标构建模型，得出了最优的销售定价和回收定价，并对模型进行了数值仿真分析。孙晓东等[8]建立了一个基于质量差别产品的单周期收益定价及定质模型，首先根据产品的质量和价格建立产品的售出概率模型，然后以售出概率模型为基础建立了以收益最大化为目标的非线性规划模型，从而确定不同质量水平产品的质量和最优价格。徐峰等[9]建立了WTP差异下的再制造产品差异定价模型和单一定价模型，在一系列的假设前提下，对模型进行了理论分析和系统仿真，分析了各个参数对模型最优解的影响。

本文在借鉴国内外相关报废汽车资源化产品定价决策的基础上，构建与求解基于制造商利润最大化的三产品联合定价模型，并进行数值仿真分析。为此，接下来本文将基于3种产品之间的质量差异和WTP差异，运用效用理论构建产品需求函数。

1需求函数构建

1.1假设条件

1)用报废汽车的废旧程度来近似表示零部件的质量。废旧程度是表示废旧产品的功能或使用价值占全新产品功能或使用价值的比率。假设从报废汽车上拆解下来的各个零部件的废旧程度为w，w是取值在[0,1]之间的随机变量，其概率密度函数为f(w)，分布函数为F(w)，当w=0时，表示该零部件完全失去了使用功能，即处于完全报废的状态，w值的增加代表该零部件的质量增加。当w=1时，表示该零部件质量与新产品相同，当然，w取值为0及取值为1是两种极端状态，一般情况下，w取值为0到1之间的某个数[10]。

2)假设汽车零部件再制造产品和新产品质量一样，但由于再制造产品在消费者心中仍然是一种“旧产品”，故消费者对两种产品的支付意愿是不同的。显然，消费者对再制造产品的支付意愿不大于其对新产品的支付意愿，设θr为消费者对再制造产品的接受度，θr∈[0,1]，则当消费者对新产品的支付意愿为v时，对相应再制造产品的支付意愿为θrv。θr=0表示消费者对再制造产品的接受度为0，即消费者没有购买再制造产品的意愿，θr=1表示消费者对新产品和再制造产品的支付意愿是相同的，在二者价格相同的情形下，消费者对二者的需求无差异。假设该汽车零部件的市场容量，即售价为0时该产品的销量为S，消费者对新产品的估价v服从[0,S]的均匀分布[11]。

3)由于汽车零部件再利用产品并未经过再生产过程，而是直接从报废汽车车体上拆解下来直接进行销售，虽然其使用寿命并未终止，但仍存在一定的废旧程度，故再利用产品除了在消费者心中产生了“旧产品”的形象之外，其本身的质量是远远达不到新产品的质量的，故假设消费者对再利用产品的接受度θu=wθr，且θu∈[0,1]，则当消费者对新产品的支付意愿为v时，对相应再利用产品的支付意愿为θuv，且当w=1，θr≠1时，θu=θr，即消费者对再利用产品和对再制造产品的支付意愿相同，只有同时满足w=1，θr=1时，消费者对新产品、再利用产品及再制造产品的支付意愿均相同，也就是说如果制造商为这3种类型的产品制定相同的价格时，消费者对这3种产品的需求无差异[12]。

4)假设一个消费者在一个销售周期内最多购买一单位新产品或再制造产品或再利用产品[5]。

其余符号假设条件如下：pn为新产品的销售价格；pr为再制造产品的销售价格；pu为再利用产品的销售价格。可知，pn>pr>pu。

1.2函数构建

综上分析可知，消费者购买新产品、再制造产品及再利用产品的效用函数Mn、Mr及Mu分别为

Mn=v-pn，

(1)

Mr=θrv-pr，

(2)

Mu=θuv-pu=wθrv-pu。

(3)

由于θr∈[0,1]，w∈[0,1]，故wθr∈[0,1]。由式(3)可看出，即使w=1，也就是说即使再利用产品的质量跟新产品一样，但由于消费者的认知差异，消费者对再利用产品的支付意愿仍不大于其对新产品的支付意愿，从而更贴近现实状况。

对上述效用函数进行分析，可知如下结果。

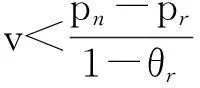
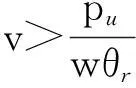
4)当Mn<0，Mr<0且Mu<0时，消费者既不购买新产品，也不购买再制造产品和再利用产品。

2定价模型构建及求解

2.1模型假设

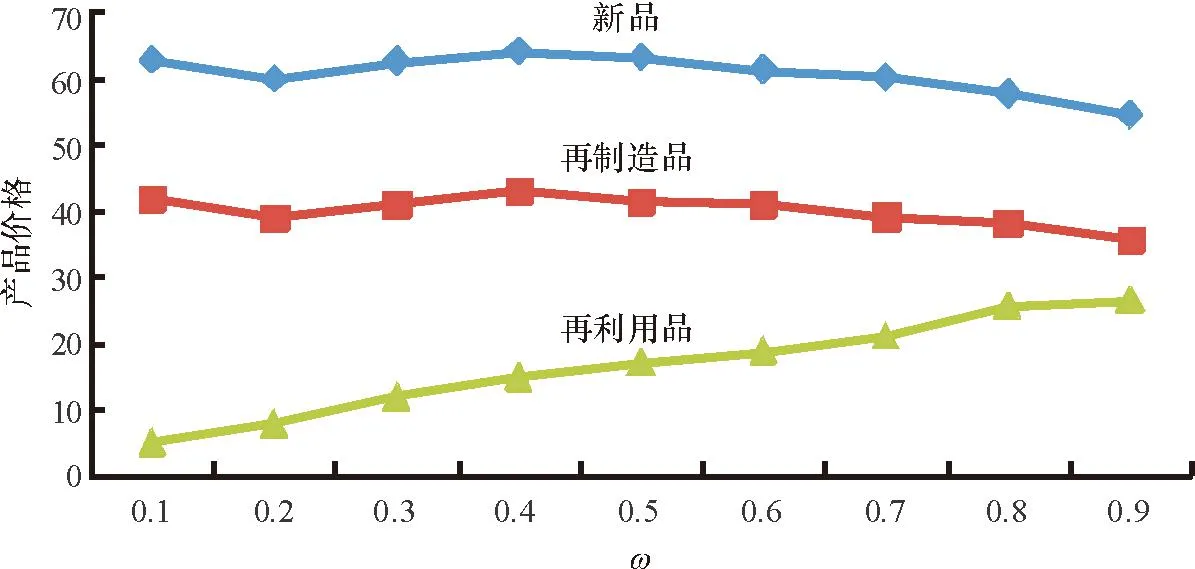
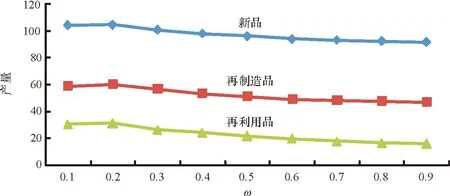
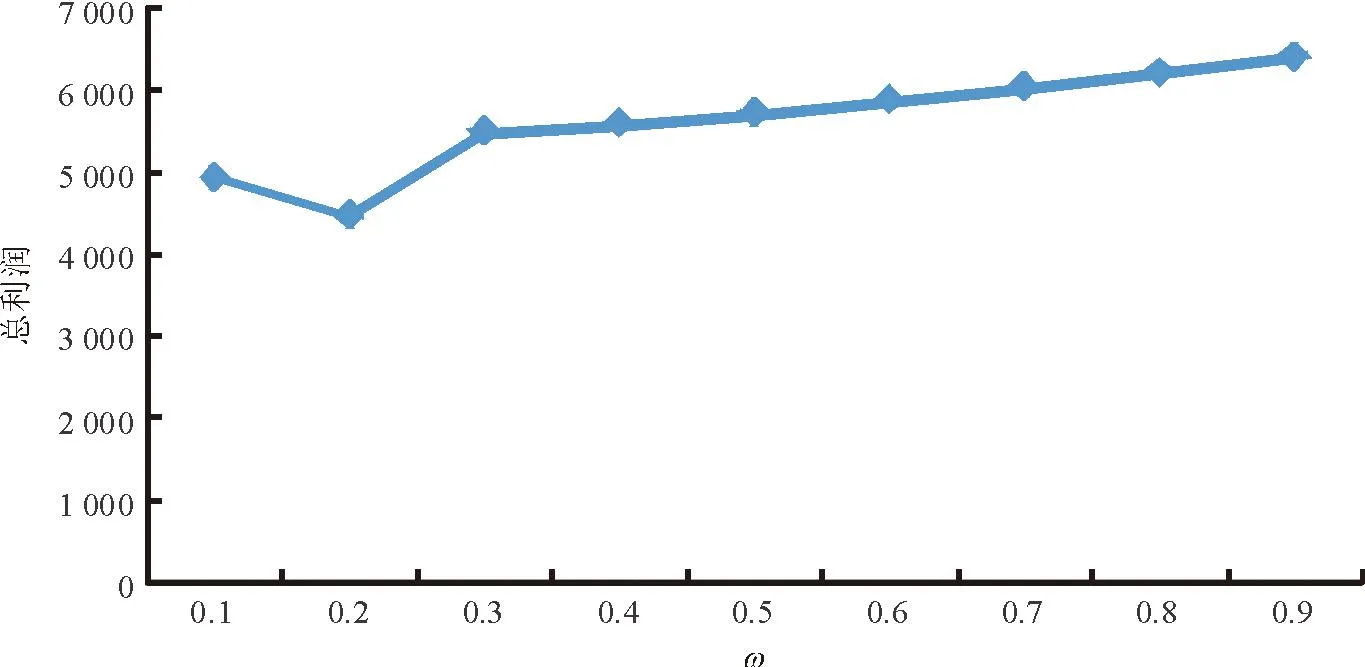
1)假设报废汽车回收率为k(0

2)假定市场上对3种产品的需求是不确定的，设新产品市场需求Dn=dn+εn，再制造产品的市场需求Dr=dr+εr，再利用产品的市场需求Du=du+εu，其中εn、εr和εu分别为独立于pn、pr和pu的随机变量，且三者相互独立，其概率密度函数分别为fn(·)、fr(·)、fu(·)，分布函数表示为Fn(·)、Fr(·)、Fu(·)。

3)假设一个消费者在一个销售周期内最多购买一单位产品。

4)假设回收的报废汽车数量足以满足制造商生产再利用产品的需求。

其余符号假设条件如下。

cn、cr、cu分别为新产品单位生产成本(包括原材料耗费、生产、包装、检测等成本)、再制造产品单位生产成本(包括运输、拆解、检测、加工及包装等成本)及再利用产品单位生产成本(包括运输、拆解、检测及包装等成本)，cn>cr>cu>0。

Qn、Qr、Qu分别为新产品产量、再制造产品产量及再利用产品产量。

tn、tr、tu分别为新产品单位缺货成本、再制造产品单位缺货成本及再利用产品单位缺货成本。

gn、gr、gu分别为新产品单位残值收益、再制造品单位残值收益及再利用品单位残值收益。

2.2模型构建

令ωn=Qn-dn，ωr=Qr-dr，ωu=Qu-du，有

新产品期望利润Πn=

(4)

再制造品期望利润Πr=

(5)

再利用品期望利润Πu=

(6)

将1.2节中dn、dr和du的值分别代入式(4)～(6)中，得三产品联合定价模型为：

cu)-tu(z-ωu)]fu(z)dz。

(7)

s.t.

dr+ωr+du+ωu≤r(dn+ωn)；

(8)

(9)

(10)

pn,pr,pu≥0；

(11)

0≤gn≤pn，0≤gr≤pr，0≤gu≤pu；

(12)

tn,tr,tu>0。

(13)

约束条件(8)为再利用资源约束；约束条件(9)与(10)为消费者对3种产品均存在需求的前提条件；约束条件(11)为销售价格的非负约束；约束条件(12)表明未销售完的产品单位残值为正，且小于市场销售价格；约束条件(13)表明缺货费用为正。

2.3模型求解

由于目标函数为凹函数(限于篇幅，证明略)，故运用Karush-Kuhn-Tucker优化条件求解，构造其Lagrangean函数为：

β2(pr-gr)+β3(pu-gu)。

(14)

Karush-Kuhn-Tucker优化条件如下：

(15)

(16)

(17)

(18)

(19)

(20)

λ1[r(dn+ωn)-(dr+du+ωr+ωu)]=0。

(21)

(22)

(23)

(24)

β1(pn-gn)=0。

(25)

β2(pr-gr)=0。

(26)

β3(pu-gu)=0。

(27)

λ1,λ2,λ3,λ4,β1,β2,β3≥0。

(28)

联立式(15)～式(28)，即可得到各决策变量的最优解，由于此模型属于非线性优化问题，难以求出显性解，故接下来将对模型进行数值仿真分析，得出最优解并进一步分析关键参数对最优解的影响。

3数值仿真分析

数据假设如表2所示，并假设εn、εr、εu均服从U(0,3)的均匀分布[5]。

表2　数据假设

将上述各参数代入式子(15)～(28)，并运用Maple软件求解可得最优解如表3所示。

表3 模型最优解

限于篇幅，仅分析再利用产品质量对3种产品定价、产量及利润的影响。固定除w外的其余参数值不变，w分别取0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9，代入模型中进行求解，得出3种产品定价、产量及总利润随质量变化的趋势如图2～图4所示。

图2　产品定价随再利用产品质量变化规律

由图2～图4可得以下结论。

结论1 从图2可知，随着再利用产品质量的增加，新产品价格和再制造产品价格总体呈下降趋势，且当w=0.9时，二者的价格达到最低。具体表现为：当w取值为[0.1,0.2]之间时，新产品和再制造产品价格呈较大幅度的下降趋势，这是由于再利用产品质量增加较为明显的原因；而当w取值为[0.2,0.4]之间时，二者的价格反而呈上升趋势，但上升速度越来越小，这是由于再利用产品质量虽增加，但消费者对其增加幅度已经不敏感，故此时二者的价格反而上升了；当w取值为[0.4,0.9]之间时，二者的价格呈下降趋势，且下降速度越来越快，这是由于再利用产品质量增加较为明显所致。随着w的增加，再利用产品本身的价格总体呈上升趋势，具体变现为：当w取值为[0.1,0.3]之间时，再利用产品价格上升速度越来越大；当 w取值为[0.3,0.6]之间时，再利用产品价格上升速度较为稳定；当w取值为[0.6,0.8]时，再利用产品价格上升速度越来越大；当w取值为[0.8,0.9]时，再利用产品价格上升速度变慢。这表明再利用产品的质量并不是越高越好，到了一定区间后，提高再利用产品质量的效果并不明显。

图3　产量随再利用产品质量变化规律

图4　总利润随再利用产品质量变化规律

结论2从图3可知，随着再利用产品质量的增加，新产品产量、再制造产品产量和再利用产品产量总体呈下降趋势，且当w=0.9时，三者的产量达到最小。具体表现为：当w取值为[0.1,0.2]时，三者的产量有均有所增加，且新产品和再制造产品产量的增加幅度大于再利用产品产量的增加幅度；当w取值为[0.2,0.9]时，三者的产量均呈下降趋势，且下降速度越来越快。此外，无论w取何值，再利用产品的产量始终低于再制造产品产量，而再制造产品产量始终低于新产品产量。

结论3从图4可知，随着再利用产品质量的增加，制造商利润总体呈上升趋势，且当w=0.9时，利润达到最大。具体表现为：当w取值为[0.1,0.2]时，这是由于质量提高不明显，制造商利润下降；当w取值为[0.2,0.4]时，总利润增加，但增加速度越来越小，这是由于质量虽提高了，但仍旧不明显的原因；当w取值为[0.4,0.9]时，总利润增加，且增加速度越来越快，这是由于质量有了明显变化的原因。

综上所述，3种产品的定价、产量及制造商总利润的变化趋势随w的变化而呈现阶段性的变化，但总体来看，随着再利用产品质量的提高，新产品价格和再制造产品价格呈下降趋势，再利用产品价格呈上升趋势，3种产品的产量呈下降趋势，制造商利润呈上升趋势。这说明制造商应致力于提高汽车零部件再利用产品的质量，如引进先进的拆解设施设备、提高拆解工人的技术水平等等，至于提高多少，应注重其变化幅度对消费者的敏感度。

4结语

本文在市场需求不确定的环境下，基于产品质量差异和WTP差异，研究了一个同时生产资源化产品和新产品的汽车零部件制造商的产品联合定价问题，并分析了质量参数对于产品定价、产量及制造商总利润的影响，结果表明：随着再利用产品质量的提高，新产品价格和再制造产品价格总体呈下降趋势，再利用产品价格总体呈上升趋势，3种产品的产量呈下降趋势，制造商利润总体呈上升趋势。

本文假设报废汽车回收率为一个常量，而实际运作当中，报废汽车回收率与回收价格、回收质量等息息相关，将来可研究报废汽车回收率参数为不确定变量的情形。

参考文献：

[1]向永华,姚巨坤,徐斌士.废旧机电产品资源化的基本途径及支撑条件[J].中国资源综合利用,2004(2):28-30.

XIANG Yonghua, YAO Jukun, XU Binshi. Basic approach and supporting condition of waste electromechanical products recycling[J]. China Resources Comprehensive Utilization,2004(2):28-30.

[2]代应.废旧汽车资源化逆向物流运作管理研究[D].重庆：重庆大学，2008.

DAI Ying. Research on reverse logistics operation management of waste automobiles for resource recovery[D].Chongqing： Chongqing University，2008.

[3]霍佳震,李贵萍,段永瑞.部分延迟订购的易变质品联合定价与生产策略[J].运筹与管理,2015,24(1):255-262.

HUO Jiazhen, LI Guiping, DUAN Yongrui. Joint pricing and production policy for deterioration items with partial backlogging[J].Operations Research and Management Science,2015,24(1):255-262.

[4]孙彩虹.部分信息下联合鲁棒定价、订货决策的报童模型[J].系统工程理论与实践,2014,34(5):1122-1130.

SUN Caihong. Jointly robust pricing and order decision newsvendor model under the limited information[J]. Systems Engineering—Theory & Practice, 2014,34(5):1122-1130.

[5]郭军华,杨丽,李帮义,等.不确定需求下的再制造产品联合定价决策[J].系统工程理论与实践,2013,33(8)：1949-1955.

GUO Junhua, YANG Li, LI Bangyi, et al. Jointed pricing decision of remanufacturing system under uncertain demand[J]. Systems Engineering—Theory & Practice,2013,33(8)：1949-1955

[6]林欣怡，孙浩，达庆利.随机环境下再制造产品的定价策略研究[J].运筹与管理,2012,21(3):148-153.

LIN Xinyi, SUN Hao, DA Qingli. Research on pricing policies of remanufactured products under stochastic environment[J]. Operations Research and Management Science,2012,21(3):148-153.

[7]李响，李勇建，蔡小强.随机产率和随机需求下的再制造系统的回收定价决策[J].系统工程理论与实践，2009,29(8):19-27.

LI Xiang, LI Yongjian, CAI Xiaoqiang. Collection pricing decision in a remanufacturing system considering random yield and random demand[J]. Systems Engineering—Theory & Practice,2009,29(8):19-27.

[8]孙晓东，田澎，曹云，等.质量差别产品的收益管理描述及定价策略分析[J].工业工程与管理,2008，11(1):83-89.

SUN Xiaodong, TIAN Peng, CAO Yun， et al. Revenue management definition and pricing strategy analysis for quality differentiation products[J]. Industrial Engineering and Management,2008,11(1):83-89.

[9]徐峰,盛昭瀚,陈国华.基于异质性消费群体的再制造产品的定价策略研究[J].中国管理科学，2008,16(6):131-136.

XU Feng, SHENG Zhaohan, CHEN Guohua. The remanufactured products pricing strategy in a heterogeneous market[J]. Chinese Journal of Management Science,2008,16(6):131-136.

[10]苏琳.需求不确定下考虑质量的回收定价策略研究[D].沈阳：东北大学,2011.

SU Lin.Study on recycling pricing with quality considered under the uncertainty of demand [D].Shenyang:Northeastern University,211.

[11]FERGUSON M, TOKTAY L B. The effect of competition on recovery strategies [J]. Production and Operations Management, 2006, 15(3):351-368.

[12]FERRER G, SWAMINATHAN J M. Managing new and remanufactured products[J].Management Science,2006,52(1)：15-26.

A Research on Jointed Pricing Decision of ELVs RecyclingProducts Based on Quality Differentiation and WTP Differentiation

CAI Keyuan, ZOU Ye, WANG Zengqiang

(School of Transportation & Logistics, Southwest Jiaotong University, Chengdu 610031,China)

Abstract：In order to price the recycling products orderly and reasonably, the jointed pricing decision of new auto parts, remanufactured auto parts and reusable auto parts under uncertain demand from the perspective of the solo manufacturer are focused on. Firstly, product demand function is set using utility theory based on quality and willingness to pay(WTP)differentiation of above-mentioned new products, remanufactured products and reusable products. Then a jointed pricing model of products is built based on product demand function, and the solutions of the model are analyzed numerically. The results show that the new and remanufactured product’s pricing and three products’ productivity will decrease while the reusable product’s pricing and manufacturer’s profit will increase with the increase of quality of reusable products.

Key words：quality differentiation; willingness to pay(WTP)differentiation; jointed pricing; end-of-life vehicles (ELVs)

收稿日期：2015-09-21

基金项目：国家自然科学基金资助项目(71401142)

作者简介：蔡克元(1990-)，男，安徽省人，硕士研究生，主要研究方向为逆向物流.通讯作者：王增强(1982-)，男，山西省人，博士，主要研究方向为逆向物流； E-mail：wzqlinger@126.com.

doi:10.3969/j.issn.1007- 7375.2016.02.007

中图分类号：F224

文献标志码：A

文章编号：1007-7375(2016)02- 0038- 07