关于级数论的教学法探究
2016-06-16何天荣丽江师范高等专科学校数计系云南丽江674199
何天荣(丽江师范高等专科学校数计系 云南丽江 674199)
关于级数论的教学法探究
何天荣(丽江师范高等专科学校数计系云南丽江674199)
摘要:级数理论是数学分析课程的一个重要知识模块,它与微积分学一起作为数学分析的重要组成部分,二者共同以极限为基本工具,分别从离散与连续两个方面,结合起来研究分析学的对象,即变量之间的依赖关系─函数。但因为级数理论与微积分学之间的逻辑联系相对较少,所以学生学习这部分知识时回感觉比较孤立加之理论抽象,所以学起来会比较吃力,知识点容易遗忘,本文从级数理论的作用、知识间的逻辑联系、及其所蕴含的思想方法等方面进行教法探究 。
关键词:级数论;教学法;数学分析。
【DOI】10.19312/j.cnki.61-1499/c.2016.04.069
一、级数理论的重要作用
数学分析课程的研究对象是函数,而级数是研究函数的一个重要工具,在理论上和实际应用中都处于重要地位,虽然初等函数能够描述许多自然现象和工程技术中的客观规律,但是,只有初等函数还远远不能满足描述客观规律的要求。为了使数学分析所讨论的函数能广泛地服务于科学技术和数学理论本身,人们借助于极限、函数方程、微分和积分等工具表述了更多的非初等函数,借助级数表示许多常用的非初等函数,微分方程的解就常用级数表示;另一方面又可将函数表为级数,从而借助级数去研究函数,例如用幂级数研究非初等函数,以及进行近似计算等。
二、级数理论及知识点间关系
数学分析课程中的级数理论包括《数项级数》、《函数列与函数项级数》、《幂级数》和《傅里叶级数》四章的内容。本文以前三章为例研究知识点间的联系。
数项级数简单地说就是,无限个数相加的问题,即将数列的各项依次用加号连接的结果问题。需要我们研究的问题:无限和是否存在及如何求其和?这就是要研究的数项级数的核心问题:级数的收敛性及其和问题。
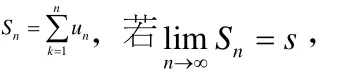

讨论函数项级数的一致收敛性的作用在于,一致收敛的函数项级数有非常理想的分析性质:如无限和运算与积分运算可以交换次序。

本例通过交换积分运算与求和运算使得运算顺利完成。
幂级数是一类简单的函数项级数,因为它的特殊性,使得我们的研究可以进一步深入,对于幂级数的学习目标是研究其收收敛域,而要研究收敛域,首先要研究其收敛半径,有了收敛半径R,就可以得出收敛区间(-R,R),收敛区间及其在区间端点±R处的收敛性,就可以讨论出幂级数的收敛域。
函数的幂级数展开就是函数项级数表示非初等函数的具体方法,也是我们研究函数项级数的一个重要原因。
三、关于级数理论的学习建议
1.注意知识点间的逻辑联系
级数论的编排的逻辑顺序是首先研究数项级数,它是函数项级数的特殊情况,是相对简单却又非常重要的内容,已经分析过,函数项级数一致收敛性的判别、幂级数的收敛性域的讨论最终都要借助于数项级数尤其是正项级数收敛性的判别;其次,要特别注意概念间的区别及本质原因,如数项级数的收敛性函数项级数的一致收敛性,要弄清楚为什么会有不同的概念及其原因。幂级数是特殊的函数项级数,因此关于幂级数收敛半径是求法,其理论依据来源于函数项级数的相关理论,而区间端点处收敛性的讨论则归结为数项级数收敛性的判别法。
2.注重其中所蕴含的思想方法
首先,类比的思想方法,数项级数、函数项级数以及幂级数同为级数,讨论的核心都是收敛性,但又因为三者之间有本质的区别,所以讨论的方法又不尽相同。学习中要充分利用其相似之处便于降低理解的难度同时要深刻理解其不同之处并理解其本质区别,才可以真正学懂级数论。
其次是化归思想方法,化归思想方法广泛存在于数学的各学科之中,许多数学问题的解决都体现了化归思想,级数论也不例外,上述已分析,函数项级数的一致收敛性性的M判别法、幂级数收敛域的讨论最终都化归为数项级数收敛性的判别法,如果透彻理解化归思想并学透数项级数,级数论的学习将不再那么抽象。
参考文献:
[1]顾泠沅.数学思想方法[M].北京:中央广播电视出版社,2004.
[2] 华东师大数学系编.《数学分析》(第三版)[M] 北京:高等教育出版社 2010.
作者简介:
何天荣(1979—)女,讲师,硕士研究生,主要从事模糊集理论和粗糙集理论及教育教学法的研究。
