光照变化条件下的人脸识别
2016-06-16全雪峰
全雪峰
(南阳医学高等专科学校卫生管理系 南阳 473061)
光照变化条件下的人脸识别
全雪峰
(南阳医学高等专科学校卫生管理系南阳473061)
摘要为降低光照变化对人脸识别准确率的影响,该文提出了一种基于形态学高低帽变换、同态滤波和奇异熵的人脸识别方法。首先用高低帽变换和同态滤波对人脸图像进行处理,然后分别提取图像的整体奇异熵和分块奇异熵,以此构成最终分类特征,最后通过支持向量机对其分类。在Yale人脸库上的实验表明,该方法具有较高的识别率和光照鲁棒性。
关键词人脸识别高帽变换低帽变换同态滤波奇异熵
一、引言
人脸识别技术可广泛应用于金融、考勤、公共安防等领域,已成为当前模式识别领域的一个研究热点[1-4]。在人脸识别过程中主要涉及人脸检测、特征提取和人脸分类几个方面[5],其中征提取是人脸识别系统中最重要一环。有效的特征提取工作将使识别的性能大大提高。在特征提取方面目前已有许多方法,如主成分分析法(PCA)、线性判别分析法(LDA)、独立成分分析法(ICA)等[6-8]。但是这些方法很容易受光照等因素的干扰[9],影响最终识别效果。为了克服光照的影响,人们提出了多种方法,大致可以分为图像预处理、光照不变特征提取两类。图像预处理包括直方图、Gamma校正等[10-11],通过预处理将不同光照条件下的人脸图像变换到同一光照条件,然后提取人脸特征。光照不变特征如Gabor、LBP、LDP等[12-14],这些特征不随光照变化而发生显著的改变。同态滤波器是一种处理光照不均引起图像质量下降的有效方法[15],但该方法最佳参数的选择是一难点。高低帽变换是常用的数学形态学变换,该变换利用合适的结构元素,将需要的目标从复杂的背景中提取出来,进而达到对人脸识别的目的[16],但其缺点是会降低图像的对比度[17]。本文结合高低帽变换和同态滤波各自的优点,对人脸图像进行预处理,并采用奇异熵作为人脸特征和支持向量机相结合,形成完整的人脸识别方法。最后在Yale人脸库上对所提出的方法进行了测试。
二、相关工作
1、高低帽变换
高低帽变换是基于膨胀和腐蚀的形态学变换,是一种极好的高通滤波算子[18]。根据使用开、闭运算的不同而分为开top-hat(高帽)变换和bot-hat(低帽)变换。其中top-hat变换的定义如下:
而bot-hat变换的定义如下:
top-hat变换能检测图像中的峰,bot-hat变换能检测图像中的谷。对于灰度图像分析,这对从较亮背景中求暗的像素聚集体或从较暗背景中求亮的像素聚集体非常有效[19]。
2、同态滤波
灰度图像f(x,y)可表示为照射分量与反射分量的乘积形式。假设照射分量为i(x,y),反射分量为r(x,y),则图像f(x,y)可以表示为[20]:
一幅图像的照射分量i(x,y)主要体现图像的光源条件,其频谱特征以低频成分为主;反射分量r(x,y)取决于图像边缘、细节等特性,其频谱特征以高频成分为主。同态滤波原理是通过降低图像的低频分量、增大高频分量来降低光照不均对图像造成的影响,具体实现过程如图1所示。
在图1中,ln表示对原始图像f(x,y)取对数,DFT表示傅里叶变换,IDFT表示傅里叶逆变换,Exp表示指数运算,g(x,y)表示经过同态滤波后的图像。
由图1可知,同态滤波的滤波效果关键在于传递函数H(u,v)的选择。传统的同态滤波函数有基于巴特沃思高通滤波器修改得到的同态滤波函数和基于高斯滤波器修改得到的同态滤波函数。本文选择高斯同态滤波器进行滤波,其滤波函数如下:
式中,rH表示高频增益,rL表示低频增益,D(u,v)表示频率(u,v)到滤波器中心的距离,D0表示截止频率。
3、奇异值分解和奇异熵
定理1(SVD):若A∈Rm×n,则存在两个正交矩阵U= [u1,u2,…,um]∈Rm×m和V=[v1,v2,…,vn]∈Rn×n,使得
奇异值对于矩阵元素的扰动变化不敏感,具有相对稳定性,以及位移不变性、旋转变不变性和镜像变化不变性等重要性质。这些特性表明,当人脸图像存在噪声或是在不同条件下获得时,奇异值可以作为人脸图像一种有效的代数特征[4]。
图像矩阵的奇异值可以对图像的信息量作出客观反映,不同图像的奇异值存在差异。为定量衡量差异大小,本文引入奇异熵概念,其定义式如下[21]:
式中r为非零奇异值个数。
4、支持向量机
支持向量机[22](Support Vector Machine,SVM)是由Vapnik等人提出的一种机器学习方法,可用于分类和回归研究。SVM处理分类问题的基本思想是[23]:首先应用某种核函数(如线性核函数、多项式核函数、径向基核函数等)将输入的训练样本映射到高维特征空间F中;然后在高维空间F中找到一个能将这些样本分开的最优超平面,使其泛化和推广能力最强;最后,将待测样本投影到高维空间,由投影点相对于最优超平面的位置来确定待测样本的类别。
三、算法设计
在上述工作的基础上,本文提出光照变换条件下人脸识别算法,具体步骤如下:
1、Step 1人脸图像几何归一化。采集到的人脸图像往往大小不一,需对图像进行几何归一化,使图像中人眼位置处于同一水平坐标轴上,并将图像大小归一化为64×85。
2、Step 2对几何归一化处理后的图像先执行top-hat变换,然后执行bot-hat变换,最后执行同态滤波,用以消除由于光照不均带来的影响。
3、Step 3人脸特征提取。在提取人脸特征时,如果只提取整幅图像特征,这样得到的是图像的整体特征,缺乏对对细节的描述。为此,本文提出了一种基于整体与局部相结合的人脸特征提取算法,具体步骤如下:
(1)对整幅图像进行奇异值分解,得到该图像的一个奇异值向量,利用公式(6)计算该图像的整体奇异熵Eall;
(2)将人脸图像分成划分为4×5共20个子块,对每一个子块进行奇异值分解,得到相应的奇异值向量,利用公式(6)计算不同子块的奇异熵Ei(i = 1,2,…,20);
(3)将整体奇异熵与分块奇异熵组合,构成一个包含21个奇异熵的奇异熵向量E=[Eall,E1,E2,…,E20],作为最终人脸特征。
4、Step 4利用SVM进行人脸分类。本文采用Matlab 2014a和SVM工具箱libsvm作为实验平台。libsvm是台湾大学林智仁教授等设计开发的,具有多分类功能,可以选择多种函数作为核函数[24],本文使用径向基函数作为核函数。
四、实验结果与分析
1、数据来源
本文实验数据取自Yale人脸库。该人脸库包含15人,每人11幅,大小为320×243像素,灰度级为256,共165幅人脸图像。这些图像是在不同光照条件、不同姿态和不同表情下拍摄的。实验前按第2节所述对图像几何归一化。实验时取每人的前5幅图像构成训练集,后6幅图像构成测试集,按照第2节所述算法进行训练和测试。
2、高低帽变换参数的影响
在高低帽变换中选取不同的结构元素处理图像后的效果如图2所示。
其中,不同结构元素的参数如下:se1 = strel('octagon',3),se2 = strel('ball',3,2),se3 = strel('diamond',1),se4 = strel('disk',1),se5 = strel('line',1,45),se6 = strel('rectangle',[22]),se7 = strel('square',3)。
由图2可以看出,当结构元素选取square时,对图像有较好的增强效果,因此本文结构元素选取square。
结构元素square参数对人脸图像识别率的影响如图3所示。
由图3可以看出,结构元素square边长对人脸识别率有较大影响,当边长取6时识别率达到最高值93.3%。本文取结构元素square的边长为6。
3、同态滤波器参数的影响
同态滤波器参数对人脸识别率的影响如表1所示。其中,条件1是未结合高低帽变换;条件2是先对图像进行高低帽变换,然后进行同态滤波。

表1 同态滤波器参数rH和rL取不同值时的识别率(%)
由表1可以看出,同态滤波器消除光照不均匀的程度较大的依赖于参数的选取。但是结合高低帽变换后,可以弱化同态滤波器参数的影响,提高人脸识别率。
4、不同算法的比较
为验证本文所提算法的有效性,对几种不同人脸识别算法进行了比较,如表2所示。其中,算法1用奇异值做特征,未进行高低帽变换和同态滤波,利用SVM进行分类;算法2采用奇异熵做特征,未进行高低帽变换和同态滤波,采用SVM进行分类;算法3为文献[7]的方法。
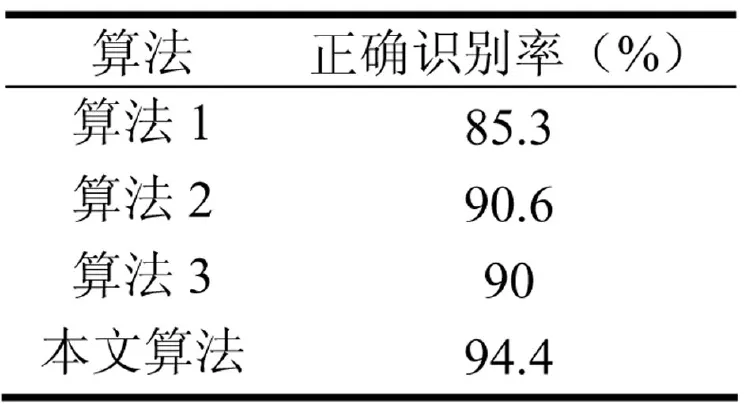
表2 不同算法比较
由表2可以看出,同样是采用奇异熵做人脸图像特征的算法2,在未对图像进行高低帽变换和同态滤波情形下,由于光照不均的影响,其识别率低于本文算法。在没有对图像进行高低帽变换和同态滤波条件下,基于奇异值特征的算法1识别率要低于基于奇异熵的算法2识别率,且远低于本文算法识别率,这说明奇异熵特征的鲁棒性更强。此外,本文方法的识别率高于算法3的识别率。
五、结束语
本文采用形态学中的高低帽变换和同态滤波对人脸图像进行处理,从而减弱光照不均对识别率的影响。同时,采用图像的整体和分块奇异熵作为人脸特征,更具鉴别性。在Yale人脸库上的实验表明,本文提出的方法是一种较好的光照不变人脸识别算法,具有较高的人脸识别率,可用于光照变换条件下的人脸识别。
参考文献
[1]翁斌.生物识别技术在金融领域的应用[J].中国金融电脑,2015,(8):91-91.
[2]赵鹏飞.基于人脸识别的煤矿职工考勤系统设计[J].煤炭技术,2013,(11):315-316.
[3]孙文荣,周先春,嵇亚婷等.基于直方图均衡化、PCA 和SVM算法的人脸识别[J].软件,2014,35(8):11-15.
[4]李晓东,费树岷,张涛等.基于奇异值特征和支持向量机的人脸识别[J].东南大学学报(自然科学版),2008,38(6):981-985.
[5]刘晓旻,谭华春,章毓晋等.人脸表情识别研究的新进展[J].中国图象图形学报,2006,11(10):1359-1368.
[6]张岩,武玉强.一种改进的模块PCA人脸识别新方法[J].计算机工程与应用,2011,47(26):216-218.
[7]顾令飞.基于多类LDA的人脸表情识别研究[D].厦门大学,2014.
[8]周书仁,梁昔明,朱灿等.基于ICA与HMM的表情识别[J].中国图象图形学报A,2008,13(12):2321-2328.
[9]丁维福,姜威,张亮亮等.结合Gabor变换和FastICA的人脸表情识别方法[J].计算机工程与应用,2011,47 (24):178-181.
[10]杨利平,辜小花.用于人脸识别的相对梯度直方图特征描述[J].光学精密工程,2014,22(1):152-159.
[11]顾思思.复杂光照条件下的人脸预处理算法[J].计算机工程与应用,2014,(19):187-191.
[12]张文超,山世光,张洪明等.基于局部Gabor变化直方图序列的人脸描述与识别[J].软件学报,2006,17(12):2508-2517.
[13]万源,李欢欢,吴克风等. LBP和HOG的分层特征融合的人脸识别[J].计算机辅助设计与图形学学报,2015,(4):640-650.
[14]高现文,付炜.局部定向模式在人脸识别中的应用[J].计算机工程与应用,2012,48(12):198-201.
[15]齐永锋,火元莲.一种基于同态滤波器与Radon变换的光照不变人脸识别方法[J].计算机工程与科学,2015,37(12):2393-2398.
[16]王江涛,梅雪,林锦国等.基于Top-hat变换与主成分分析的人脸识别方法[J].计算机工程与设计,2009,30 (2):395-397.
[17]张欣,杜天宇.结合Top-hat变换改善同态滤波的方法[J].河北大学学报(自然科学版),2014,34(6):662-667.
[18]章毓晋.图像工程(上册)--图像处理和分析[M].北京:清华大学出版社,1999.
[19]刘玉芹,苑玮琦,郭金玉等.基于小波分解和高低帽变换的在线掌纹识别[J].计算机应用研究,2011,8(6):355-2357.
[20]刘毅,贾旭芬,田子建等.一种基于同态滤波原理的井下光照不均图像处理方法[J].工矿自动化,2013,39 (1):9-12.
[21]杨文献,姜节胜.机械信号奇异熵研究[J].机械工程学报,2000,36(12):9-13.
[22]Cortes C,Vapnik V. Support vector machine[J]. Machine Learning,1995,20(3):273-297.
[23]刘兴华,蔡从中,袁前飞等.基于支持向量机的乳腺癌辅助诊断[J].重庆大学学报(自然科学版),2007,30 (6):140-144.
[24]Chang Chin-Chung,Lin Chin-Jen. LIBSVM:A library for support vector machines[EB/OL].(2016-01-27)[2016-04-16]https://www.csie.ntu.edu.tw/~cjlin/libsvm/.
Face Recognition under Illumination Variations
Quan Xuefeng
(Department of Health Management,Nanyang Medical College Nanyang 473061)
AbstractIn order to improve the face recognition rate under illumination variations,This paper proposes a face recognition method based on top-hat transformation and bot-hat transformation,homomorphic filtering and singular entropy. Firstly,the face images are proceed with top-hat transformation,bottom-hat transformation and homomorphic filtering. Then the whole singular entropy and the block singular entropy of the image are extracted to form the final classification features. Finally,the classification of the image is classified by the support vector machine. Experiments on Yale face database show that the proposed method not only has high recognition rate but also has certain robustness to illumination.
KeywordsFace recognition Top-hat transformation Bot-hat transformation Homomorphic filtering Singular entropy
中图分类号TP391.4
文献标识码A
文章编号160514-7280
作者简介:
全雪峰(1969~),男,河南淅川人,硕士,讲师,主要研究方向:智能信息处理。
