水下机械手水动力学模型及仿真
2016-06-15朱雅乔
李 琪, 朱雅乔
(1.中车长春轨道客车股份有限公司 国家轨道客车工程研究中心车体研发部,吉林 长春 130000;2.天津中德职业技术学院 航空航天与汽车学院,天津 300350)
水下机械手水动力学模型及仿真
李琪1,朱雅乔2
(1.中车长春轨道客车股份有限公司 国家轨道客车工程研究中心车体研发部,吉林 长春130000;2.天津中德职业技术学院 航空航天与汽车学院,天津300350)
摘要:以Morison公式为基础,研究了浮力、水阻力、附加质量力对水下机械手的影响,结果表明,在各影响因素中,浮力影响最大,水阻力和附加质量力引起的水动力很小.以大臂关节为例分析了不同水阻系数和附加质量力系数对搅水力矩的影响,水阻力系数对搅水力矩的影响较大,而附加质量力系数对搅水力矩的影响较小.
关键词:水下机械手;水动力学模型;轨迹规划
水下机械手动力学要考虑水环境的影响,在水下机械手动力学研究中,通常是将水环境影响参数(浮力、水阻力、附加质量力、流体加速力等)融入一般机器人动力学建立的方程中[1-2].目前,对水下机械手动力学模型的研究主要采用半理论、半经验的方法,在动力学模型的基础上建立水下机械手水动力学模型[3-4].本文在对关节空间进行轨迹规划的基础上,采用数值计算、定量分析的方法对比水下机械手在空气中和水体中的动力学特性.
1水下机械手动力学模型
对比非水下机械手的动力学方程,建立水下机械手的动力学方程如下:
(1)

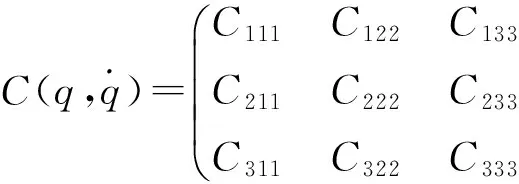

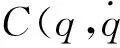







C111=0,

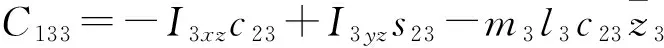

C222=0,



C333=0,


C131=2(I3yy-I3xx)s23c23,
C212=0,


C312=0,
C323=0,

G1=0,


由于关节机构中的摩擦十分复杂,并与润滑条件有关,为了便于动力学仿真,将其表示为关节角速度的函数:
(2)
式中,c为摩擦系数.
由理论力学可知,单个运动体在有流液压环境中运动时,受到的水作用力为:
(3)
文中的水下机械手处于静水环境中,所以不需要考虑水下机械手所受到的水流冲击力.
式中,Fd为水阻力,Fm为附加质量力,Fl为升力,Ff为浮力,l为单位长度.
升力Fl的产生是因为结构物有异形冲角,若结构物无机翼形状,则不计升力.
根据Morison公式,

(4)
式中,Fd,Fm分别为作用在单位长度上的水阻力和附加质量力,ρ为流体密度,Cd为阻力系数,Cm为惯性力系数,D为结构物的等效直径,V(x)为速度函数,A为物体在垂直于水流速度方向V的投影面积,dl为单元厚度.
2浮力的计算
由于重力和浮力的方向相反,需要将它们放在一起考虑,这就存在一个向下的等效重力,各连杆等效重力产生的力矩即为等效重力矩,单连杆等效重力可以表示为:
(5)
式中,mi为连杆i的质量,g为重力加速度,Vi为连杆i的有效体积,ρ为水的密度,ρm为连杆i的材料密度.
G1=0,
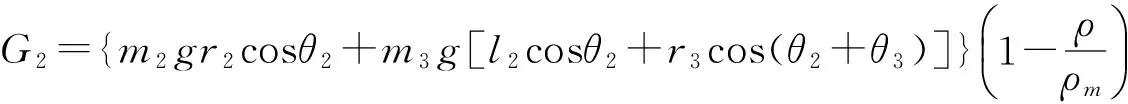
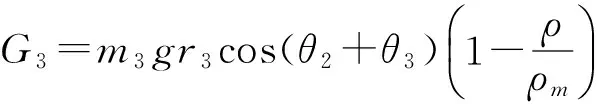
其中,Gi为作用在连杆i上的重力.
3水阻力矩和附加质量力矩的计算
3.1水阻力矩的计算[8-9]
当物体在粘性液体中运动时,会产生水阻力,水阻力可分为法向阻力和切向阻力,如图 1所示.切向速度Vr产生切向阻力,法向速度Vn产生法向阻力.

图1 连杆水阻力分析
对于圆柱体,切向阻力很小,可以忽略不计[8],所以本文所分析的水阻力为法向阻力.

(6)
关节整体产生的阻力和阻力矩为:

(8)
其中,Td为水阻力,Cd为水阻力系数.
3.1.1腰关节所受水阻力矩Td1的计算
(9)
(11)
其中,r1-1为腰部所取微段到Z0轴的距离,r2-1为大臂所取微段到Z0轴的距离,r2-2为小臂所取微段到Z0轴的距离,ω1为腰关节角速度.
将式(9)、式(10)、式(11)代入式(8)得腰关节所受水阻力矩为:


(12)3.1.2大臂关节所受水阻力矩Td2的计算
(13)
(14)
(15)
其中,r2-2为大臂所取微段到Z1轴的距离,r3-2为小臂所取微段到Z1轴的距离,r3-3为小臂所取微段到Z2轴的距离,ω2为大臂关节角速度.
将式(13)、式(14)、式(15)代入式(8)得:



(16)
3.1.3小臂关节所受水阻力矩Td3的计算
(17)
其中ω3为小臂关节角速度.
将式(14)、式(17)代入式(8)得:

(18)
3.2附加质量力矩的计算
若物体在水中做加速运动,则周围的流体也跟随着做加速运动,物体受到水的反作用力,即为附加质量力Fm,如图2所示.

图2 附加质量效应
根据水动力学可知,连杆产生的附加质量矩为:
(19)
所以整个关节产生的阻力和阻力矩为:
(20)
(21)
3.2.1腰关节所受附加质量力矩Tm1的计算
将式(9)、式(10)、式(11)代入式(21)得:
(22)
3.2.2大臂关节所受附加质量力矩Tm2的计算
将式(13)、式(14)、式(15)代入式(21)得:
(23)
3.2.3小臂关节所受附加质量力矩Tm3的计算
将式(14)、式(17)代入式(21)得:

(24)
由上述计算可得到水动力对机械手各关节的力矩为:
Th=[Td1+Tm1Td2+Tm2Td3+Tm3]
(25)
4水下机械手动力学仿真
4.1机械手轨迹规划
为了便于比较各参数对水下动力学的影响,采用5次B样条轨迹规划方法构造水下机械手的关节轨迹.假定机械手完成某一空间动作算例[9]时使用的结点数值如表1,各节点间的时间间隔见表2.

表1 关节结点(型值点)数值

表2 各节点的时间间隔
根据B样条轨迹规划方法编写 MATLAB程序,获得图3-图5所示的各关节指标.图3-图5分别是采用5次B样条曲线进行轨迹规划时腰关节、大臂关节、小臂关节的位移、速度、加速度曲线.由图可见,各关节的位移、速度、加速度都是平滑的.不平滑的曲线导致关节力矩的变化也是不平滑的,不平滑的关节力矩能增大机械手轨迹跟踪时的跟踪误差,使动力学仿真结果更可靠.
4.2机械手动力学仿真
根据水下机械手动力学方程和前面得到的水下机械手水动力学模型,对水下机械手进行动力学仿真.仿真时,采用数值计算、定量分析的研究方法得出水动力学中各影响因素对水下机械手动力学的影响比重,为水下机械手控制器的设计、水动力学模型简化及补偿提供指导.分析采用的机械手参数和水环境参数如表 3所示.

图3 腰关节(5次B样条)角度、角速度、角加速度曲线

图4 大臂关节(5次B样条)角度、角速度、角加速度曲线
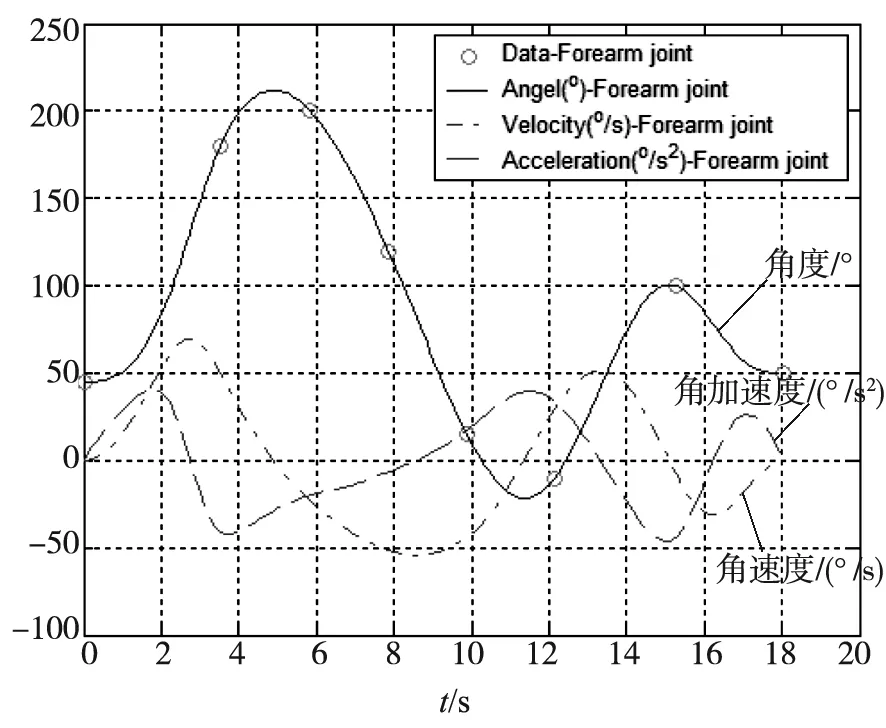
图5 小臂关节(5次B样条)角度、角速度、角加速度曲线
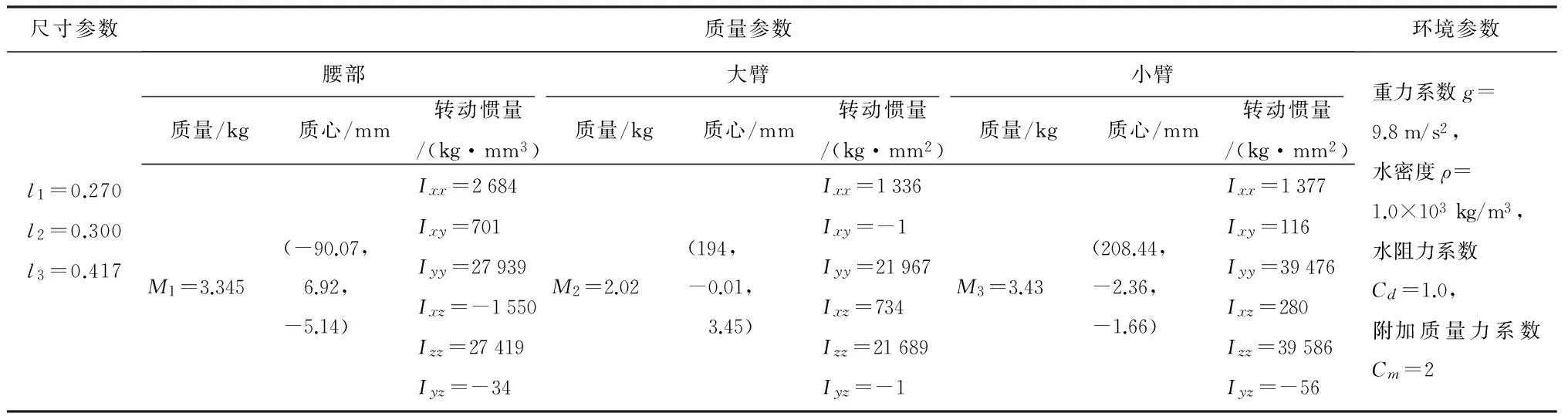
尺寸参数质量参数环境参数l1=0.270l2=0.300l3=0.417腰部大臂小臂质量/kg质心/mm转动惯量/(kg·mm3)质量/kg质心/mm转动惯量/(kg·mm2)质量/kg质心/mm转动惯量/(kg·mm2)M1=3.345(-90.07, 6.92,-5.14)Ixx=2684Ixy=701Iyy=27939Ixz=-1550Izz=27419Iyz=-34M2=2.02(194,-0.01, 3.45)Ixx=1336Ixy=-1Iyy=21967Ixz=734Izz=21689Iyz=-1M3=3.43(208.44,-2.36,-1.66)Ixx=1377Ixy=116Iyy=39476Ixz=280Izz=39586Iyz=-56重力系数g=9.8m/s2,水密度ρ=1.0×103kg/m3,水阻力系数Cd=1.0,附加质量力系数Cm=2
当机械手处在空气环境中时,不考虑浮力力矩、水阻力矩、附加质量力矩、流体加速力矩等的影响,求得机械手到达指定位置所需要的关节力矩如图 6所示.

图6 空气环境关节力矩
当机械手处在静水环境下,仅考虑浮力的影响而不计其他水动力,机械手所需的关节力矩如图 7所示.
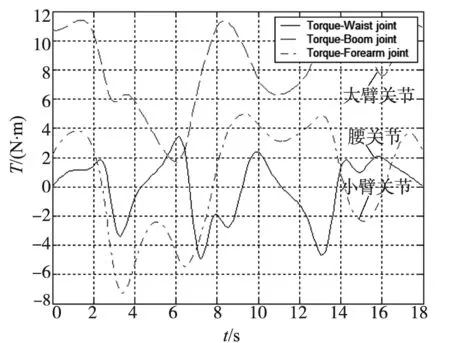
图7 静水环境关节力矩
当机械手处在静水环境下,不考虑水阻力矩和附加质量力矩时,机械手搅水引起的水动力对关节的力矩如图 8所示.
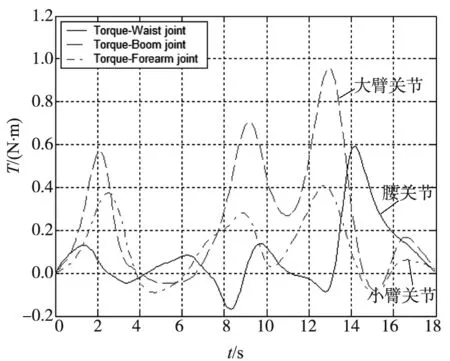
图8 静水环境搅水力矩
根据以上计算结果,对比分析图6和图7可知,由浮力引起的关节力矩变化量较大,大约为空气环境下所需关节力矩的1/3.对比分析图6和图8可知,由水下机械手搅水引起的水动力力矩大约是空气环境下所需关节力矩的1/20.
本文以腰关节为例,图9和图10分别说明了不同水阻系数Cd和附加质量力系数Cm对搅水力矩的影响,对比分析可知,Cd对搅水力矩的影响较大,而Cm对搅水力矩的影响较小.
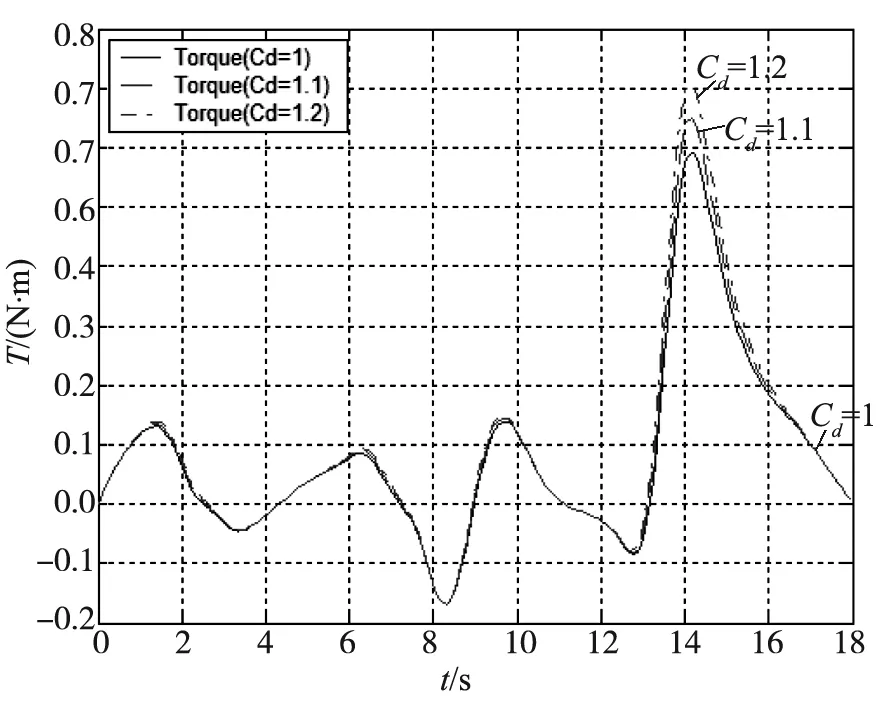
图9 不同水阻系数对搅水力矩影响

图10 不同附加质量力系数对搅水力矩影响
5结论
以Morison公式为基础建立了水下机械手的水动力学模型,在不考虑流体加速力的情况下,分析了浮力、水阻力和附加质量力对水下机械手动力学的影响.仿真结果表明,浮力产生的力矩对水下机械手动力学的影响较大,而搅水力矩的影响很小.以大臂关节为例分析了不同水阻系数Cd和附加质量力系数Cm对搅水力矩的影响,其中,Cd对搅水力矩的影响较大,而Cm对搅水力矩的影响较小.
参考文献:
[1]DANNIGAN M W,RUSSELL G T.Evaluation and Reduction of the Dynamic Coupling between a Manipulator and an Underwater Vehicle[J].IEEE Journal of Oceanic Engineering,1998,23(3):260-273.
[2]ISHITSUKA M,SAGARA S,ISHII K.Dynamics Analysis and Resolved Acceleration Control of an Autonomous Underwater Vehicle Equipped with a Manipulator[G].In proc.of 2004 Int.Symposium on Underwater Technology,2004:277-281.
[3]MCLAIN T W,ROCK S M.Development and Experimental Validation of an Underwater Manipulator Hydrodynamic Model[J].The International Journal of Robotics Research,1998,17(7):748-759.
[4]ARMENIO V.Dynamic Loads on Submerged Bodies in a Viscous Numerical Wave Tank at Small KC Numbers[J].Ocean Engineering,1998,25(10):881-905.
[5]熊有伦,丁汉,刘恩沧.机器人学[M].北京:机械工业出版社,1995:1-164.
[6]JOHN J,CRAIG.机器人学导论[M].贠超,李成群,陈心颐,等,译.北京:机械工业出版社,2012:131-159.
[7]蔡自兴.机器人学[M].北京:清华大学出版社,2000:51-81.
[8]MCMILLAN S,ORIN D E,MCGHEE R B.Efficient Dynamic Simulation of an Underwater Vehicle with a Robotic Manipulator[J].IEEE Transactions on Systems,Man,and Cybemetics,1995,25(8):1194-1206.
[9]LIN C,CHANG P,LUH J.Formulation and Optimization of Cubic Polynomial Joint Trajectories for Industrial Robots[J].IEEE Trans.On Automatic Control,1983,28(12):1066-1074.
责任编辑:金欣
Hydrodynamic and simulation of underwater manipulator
LI Qi1,ZHU Ya-qiao2
(1. Research and Development Center, CRRC Changchun Railway Vehicles Limited Company, Changchun, Jilin 130009, China;2. Aviation and Aerospace and Automobile College, Tianjin Sino-German Vocational Technology College, Tianjin 300350, China)
Abstract:Based on Morison equation, the writer studies the contribution of buoyancy, water resistance, and additional mass force to manipulator's dynamic. Result shows that buoyancy force is the most prominent. The water resistance and additional mass forces are so little that they can be ignored.The article researches on the boom joints and coefficients of water resistance and additional mass forces to the hydrodynamics in motion. Results show that water resistance coefficients are more prominent than additional mass force coefficients.
Key words:underwater manipulator; hydrodynamic model; trajectory planning
收稿日期:2015-12-08
作者简介:李琪(1989-),女,吉林松原人,中车长春轨道客车股份有限公司助理工程师,硕士;朱雅乔(1989-),男,天津人,天津中德职业技术学院助教,研究方向:特种机器人.
文章编号:1009-4873(2016)02-0017-06
中图分类号:TP241
文献标志码:A
