模糊C均值聚类算法编程实现及应用
2016-06-15马宝秋
马 宝 秋
(石家庄职业技术学院 机电工程系,河北 石家庄 050081)
模糊C均值聚类算法编程实现及应用
马 宝 秋
(石家庄职业技术学院 机电工程系,河北 石家庄050081)
摘要:模糊C均值(Fuzzy C-Means)算法是在K-Means聚类算法的基础上,利用模糊数学的原理进行的改进,讨论了它的数学原理及使用C++语言编程实现的步骤,将其应用于超声图像感兴趣区域(ROI)的检测,取得了可信的结果.
关键词:Fuzzy C-Means;聚类;算法;编程
分类问题广泛地存在于社会和自然科学中.所谓分类,就是把相似或相近的对象分到一组,让在同一个组中的成员对象都有一些相似的属性,在一个组中的各成员对象之间比不在同一组中的成员对象之间具有更多的相似性.聚类(Cluster)分析是解决分类问题的一个重要的统计分析方法[1].聚类时,不关心或者说根本不知道某一类是什么,目标是把相似的东西聚到一起.因此,聚类算法可以开始工作的前提是仅需知道如何计算相似度[1].
聚类方法非常丰富[2-3].根据K-Means聚类算法,每个数据对象都有其权重wji,由wji可构成一个矩阵,该矩阵称为隶属度矩阵,表示每个数据对象属于某个分类的“度”.由K-Means聚类的定义可知,wji不是1就是0,1代表该数据对象属于某一分类,0则相反.因为每一个数据对象只能属于一个分类,所以K-Means聚类的分类划分是一种硬聚类,它把每个数据对象严格地划分到某个类中,具有非此即彼的性质.
但是,由于分类的复杂性,硬聚类划分往往力不从心.如,对于图1所示的蝴蝶型数据,中间的点到底应该归属于左边一组还是右边一组,K-Means聚类算法就无法完成准确的划分.这种无法划分是由于蝴蝶型数据分类问题本身的硬不可分性造成的.对硬划分这是无法避免的[4].

图1 蝴蝶型数据
本文论述的Fuzzy C-Means(FCM)算法是在K-Means硬聚类算法的基础上,利用模糊数学的概念,引入概率的表示方法,对K-Means进行的“软”改进.
1FCM算法介绍
Jim Bezdek提出了基于模糊度m的基本Fuzzy C-Means(FCM)的模糊划分算法[5].FCM的目标函数定义如同K-Means聚类划分,但其权重矩阵W不再是非0即1的二元矩阵,而是应用模糊理论的概念,使用概率的表示方法,它的每一个数据对象不是仅属于某一个聚类,而是以概率的形式表现数据对象属于各个聚类的程度,称之为软聚类划分(Soft Clustering).
FCM的数学表达式为:
(1)
其中,N为数据的总数;K为聚类分类的个数;Ji为第i类聚类分类的目标函数;Xj为第j个数据;Ci为第i个聚类的中心;m为权重指数(也称为模糊度);wji为隶属度,即Xj属于聚类Ci的程度,或者说Xj属于聚类Ci的概率. wji满足以下关系:
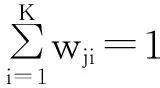
(2)
这里的隶属度wji不再是非0即1,而是一个属于[0,1]的数值.图2是一个具有10个数据、2个聚类的隶属度矩阵.

图2 模糊隶属度矩阵
从图2可以看出,每一行代表一个聚类,每一列上的数值表示该数据对象在每一个聚类中的隶属度,实际也就是属于每一个聚类的概率,即每一列数值之和为1.也就是说,每一个数据对象并不是完全属于某一个聚类,而是通过概率的形式表达该数据对象在某一个聚类中的隶属度.
2FCM算法的实现
2.1FCM算法的实现步骤
根据FCM的数学表达式所表达的算法,按照以下几个步骤即可实现本算法[5-6].
步骤1,设定K为分类个数,W为初始隶属度矩阵,W中的每个数据元素wji采用计算机伪随机给定[0,1]之间的数值,并满足(3)式.
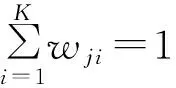
(3)
步骤2,计算每一个聚类的中心点,公式为:
(4)
步骤3,根据(1)式计算第t次和第t-1次迭代的目标函数J(t)和J(t-1),并计算J(t)和J(t-1)之间的差值.当这个差值小于设定的某个容忍误差ε时,可结束迭代运算过程,否则,执行步骤4.
E(t)=‖J(t)-J(t-1)‖<ε
(5)
步骤4,重新计算隶属度矩阵W,公式如(6)式,并返回到步骤2.
(6)
其中,Cs为本次迭代所得的每一个聚类中心.
2.2FCM算法的实现步骤
FCM算法可应用于二维灰度图像的处理,主要是将图像中的像素进行分类.例如,在人体的CT、核磁或超声图像中将人体组织的器官图像区分出来,某一个像素的灰度值与某个器官组织的整体灰度值接近的概率比较大,则其在图像中就代表该器官组织的一个像素,也就是本文所说的感兴趣区域(ROI).
与此相对应,公式(1)中的部分参数的含义变为:N为图像像素的总数,K为图像中分类的数量,Ji为第i个分类的目标函数,Xj为第j个图像像素的灰度值,Ci为第i个分类的像素灰度的中心值.
灰度图像的FCM算法在计算机中实现的步骤如下:
第一步,设定常数,包括需要分类的数目K,最大执行步骤tmax,还有一个很小但大于0的容忍误差ε以及其他需要使用的变量等.
第三步,利用嵌套循环实现算法的迭代.fort=1,2,…,tmax.
(a)forj= 1,2,…,N,计算每一个像素的隶属度,即算出隶属度矩阵.
(b)fori=1,2,…,K,更新每一个聚类分类灰度中心值.
(7)
其中,m为权重指数.
(c)判断迭代是否收敛,若式(5)成立则停止运算,否则进行下一轮迭代.
第四步,若第三步的t循环未到tmax次就结束,则表示聚类分类灰度中心值已不发生变化,误差小于ε,所得到的Ci(i= 1,…,K)即可认为是每个聚类分类的灰度中心值,即已经收敛.若t循环是因为达到tmax而结束,则表示在限定的tmax循环次数内聚类分类的灰度中心值还不稳定,可以通过增大循环次数来解决;当然,也可能是因为所聚类的灰度图像数据是发散的而没有灰度中心值.
3算法实现的注意事项
第一,在具体计算时,算法中权重指数m的取值有很多种,笔者在“基于实时超声影像的软组织形变跟踪技术”课题中,经过多次筛选,取m为2[7].
第二,判断算法收敛的方法不仅仅是利用式(5),还可以通过判断邻近两次迭代聚类中心的变化足够小,即聚类分类灰度中心值的变化小于ε来确定.
E(t)=‖C(t)-C(t-1)‖<ε
(8)
其中,C(t)和C(t-1)分别代表第t次和第t-1次迭代所得到的聚类中心.
第三,一般情况下可以采用计算机随机函数产生K个聚类中心,但是针对具体的问题可以采用其他算法粗略得到一些聚类中心的灰度值,或者直接人工选取.
第四,在二维灰度图像的应用中,通过判断计算得到的每一个图像灰度数据的隶属度,来决定其属于哪一个聚类分类,即通过判断隶属度值wji在哪一个聚类中的值最大来决定该数据的归属.
4FCM算法的应用
笔者通过上述方法在“基于实时超声影像的软组织形变跟踪技术”课题的研究中实现了FuzzyC-Means的聚类算法,并成功地应用于对软组织超声图像ROI的辨别中,所得到的FCM分割效果见图3.本应用中K取值为3,即分为3类.从图3(b)中可以看出,FCM虽然不能得到完美的ROI边缘,但是从目视的角度可以明确地区分出边缘,用于定性对比就已经足够了.
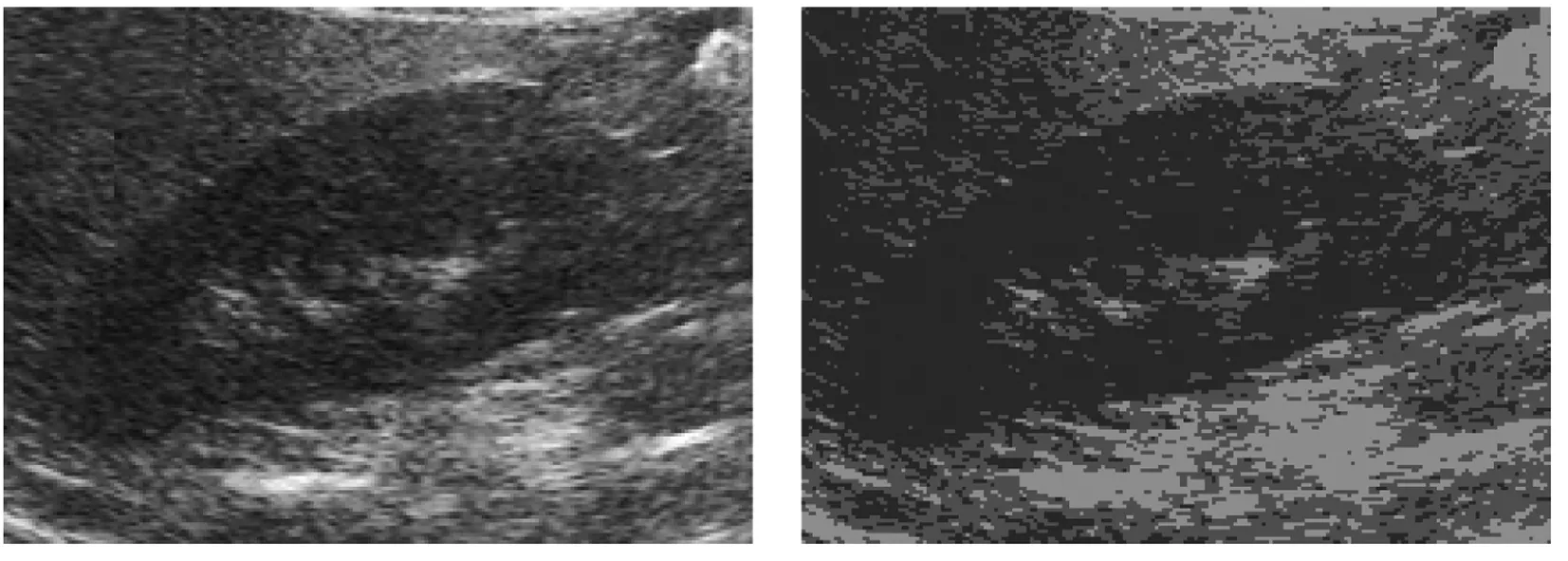
(a)肾脏原始超声图像 (b)去噪后FCM的处理效果
图3FCM分割算法处理效果
5FCM算法总结
FCM算法应用了模糊理论的概念,使得每一个输入数据不再仅归属于某一特定的聚类,而是以其归属的概率来表现它属于各聚类的程度,在运算过程中没有任何先验的知识也可以应用[1].FCM算法大多数情况下能够给出令人满意的结果,在应用中一般作为其他分析算法的预处理步骤.
FCM聚类算法也有其局限性.首先,计算前需确定聚类的数目,因此不能实现自动分类.其次,该算法对初值较敏感.初始聚类中心位置若不是理想的位置,目标函数J容易落入局部解,不能保证全局最优,可能导致分类出来的结果不理想[2].所以在实践应用中,可以多次选取初值进行运算,取其中最好的一次结果即可.再次,目前还没有确定m值的较好方法[8].文献中记载m的取值一般为[1.5,2.5],也有人提出了m的优选方法[9].m值的选择一般是从对分类结果评价的角度来进行的[10],所以m的取值仍有待于进一步研究.第四,运算量大.因为每迭代一次就需要将所有数据计算一遍,其时间复杂度为O(n3),其中n为数据对象的数量,因此,该算法的数值运算量很大,对于大的数据量往往不能进行实时运算.
6结语
本文详细讲述了FCM算法,并使用C++编程实现了本文的算法,并应用于“基于实时超声影像的软组织形变跟踪技术”课题中,实现了对软组织超声图像ROI的前期分类,为后续的图像处理打下了坚实的基础.
参考文献:
[1]李丽丽.模糊C-均值聚类算法及其在图像分割中的应用[D].济南:山东师范大学,2009.
[2]孙吉贵,刘杰,赵连宇.聚类算法研究[J].软件学报,2008,19(1):48-61.
[3]蔡元萃,陈立潮.聚类算法研究综述[J].科技情报开发与经济,2007,17(1):145-146.
[4]BEZDEK J C.Pattern Recognition with Fuzzy Objective Function Algorithms[M].New York:Plenum Press,1981:95-107.
[5]孟宪尧,韩新洁.模糊C-均值聚类算法及其在船舶故障诊断中的应用[J].中国造船,2007,48(4):98-103.
[6]张翡,范虹.基于模糊C均值聚类的医学图像分割研究[J].计算机工程与应用,2014,50(4):144-151.
[7]黄蓉.模糊C-均值聚类算法的若干研究及其在IDS中的应用[D].南京:南京邮电大学,2014.
[8]于剑.论模糊C均值算法的模糊指标[J].计算机学报,2003,26(8):968-973.
[9]高新波,裴继红,谢维信.模糊C-均值聚类算法中加权指数m的研究[J].电子学报,2000,28(4):80-83.
[10]杨燕,靳蕃,KAMEL MOHAMED.聚类有效性评价综述[J].计算机应用研究,2008,25(6):1630-1632.
责任编辑:金欣
Realization of fuzzy C-Means clustering algorithm and its application
MA Bao-qiu
(Department of Mechanics and Electrics, Shijiazhuang Vocational Technology Institute, Shijiazhuang, Hebei 050081, China)
Abstract:Fuzzy C-Means is a type of clustering algorithm that is improved by the principle of fuzzy mathematics in the K-Means algorithm. This paper discusses the mathematical principle of the fuzzy C-means clustering algorithm and the steps of using the C++ language programming. The author has applied it to the detection of the region of interest (ROI) in ultrasound images.
Key words:fuzzy C-Means; clustering; algorithm; programming
收稿日期:2016-03-02
作者简介:马宝秋(1973-),男,河北石家庄人,石家庄职业技术学院讲师.
文章编号:1009-4873(2016)02-0030-04
中图分类号:TP301.6
文献标志码:A
