问题引领,让数学课更有数学味儿——以“6的乘法口诀”为例

◇杨丽君

问题引领,让数学课更有数学味儿
——以“6的乘法口诀”为例

◇杨丽君

课前思考

在日常教学中，如何发展学生的问题意识，提高学生解决问题的能力呢？我们尝试以问题引领课堂，既有教师预设的大问题，更鼓励顺应学生的思维路径，发现学生的真问题，引导学生经历一个从头到尾思考问题的过程。

北师大版教材二年级上册“6的乘法口诀”一课，是在学生初步掌握2～5的乘法口诀的基础上进行教学的。通过前测，我们发现80%的学生能够流利地背诵出6的乘法口诀，其中有20%的学生知道乘法口诀的意义。由此看来，我们的教学活动应以学生原有的知识经验为基础，充分利用知识的迁移规律，引导学生在经历编制乘法口诀的过程中，逐步发现乘法口诀中隐藏的规律。同时，可以引导学生借助点子图、数线等模型以及运用画图等策略，帮助学生直观理解乘法口诀的意义，充分经历、体验自己建构知识的过程。那么，需要思考的是，如何在看似风平浪静的学习中，发现学生的真问题，拓展学生的思维广度呢？

表格里的规律与6有关

课始，我出示教材情境图（如图1），提出问题：看到这么多小贴画，你会想到哪些数学问题？

图1

生：有多少张小贴画？

生：一行有几张？有几行呢？

生：一行有 6张，2行有多少张？3行呢？4行呢？9行呢？

……

鼓励学生根据情境提出数学问题是问题引领的最初环节。面对学生多样的数学问题，如何有效地开展教学，增加学生的参与度呢？我选择了学生提出的“有多少张小贴画”这一问题展开讨论，以聚焦问题，理解意义。

师：今天，我们就来研究“有多少张小贴画”这个问题。你能结合这个表格（如下表），告诉大家有多少张小贴画吗？

（学生填表，然后反馈）

师：在填写表格的过程中，你有什么想法？

生1：我想问个问题，54是怎么填出来的？

师：谁能解决这个问题？

生2：我觉得是数出来的，6张6张地往上数就行了，数9个 6就得出来了。

生3：我同意生2的意见，我发现这些得数之间每次都增加6。

生4：为什么每次都增加6呢？

生2：因为一行有6张小贴画。

生3：因为每增加 1行，就要增加6张小贴画。比如，1行有6张，2行就是12张，增加了6张；3行就是18张……

生4：这样的表格里藏着规律呢，藏的规律就与6有关。

在这个过程中，原本的设计是我要提出引领性的数学问题：“这些得数之间有什么规律吗？”“为什么每次都增加6？”为了使学生从会算、会背到深入思考其中的算理。但在实际教学中，我几乎没有机会开口说话，学生的讨论推进问题的深入，发现表格中的规律与6有关，其实这既是学生对已掌握口诀的再回顾，也是对已掌握口诀意义的建构，是数学味儿加深的开始。

口诀里的秘密原来这样用

接下来，我鼓励学生借助表格与点子图，独立编制口诀。在学生编完口诀，并进行核查后，提出问题 “仔细想想，6的乘法口诀里藏着什么秘密”，让学生在小组里说说自己的发现，并进行全班交流。

师：下面我们来交流一下你发现的6的乘法口诀中的秘密。

生1：我们组发现积都是双数，6、12、18、24……一直到54，都是偶数。

生2：是的，积的个位上是6、2、8、4……都是双数。

生3：我们组发现，得数，也就是积都依次相差6。比如，6和12差 6，12和 18差 6，18和 24差6……

师：真有这样的规律吗？

生4：是啊！乘数中都有6，大家看 1×6、2×6、3×6……另一个乘数还是按照 1、2、3……9，从小到大的顺序排列的！

师：谁听懂他的意思了？

生5：他的意思是说，一个乘数是6不变，另一个乘数每增加1，积就增加6。

这时候，一个学生走上讲台，用红粉笔画出算式里的6，并提出问题：你们知道为什么到6×7、6×8、6×9，口诀就拐弯了吗？

生6：因为乘法口诀把小的数放前面，读起来会朗朗上口！

（全班立即响起赞许的掌声）

讨论与交流6的乘法口诀中的规律，是鼓励学生将识记性知识与乘法的意义理解相结合，增加其思维的深度，为后续多途径表达乘法口诀的意义做准备。

师：如果我忘记了6×7的结果是多少，你有什么好办法来帮助我吗？请你用自己喜欢的符号画一画，用点子图摆一摆，也可以用算式来写一写。

（学生开始独立思考，尝试梳理思路。教师在巡视的过程中，请有不同方法的学生到黑板上呈现自己的方法）

师：很多同学都把自己的想法写在了黑板上，快来看一看，你能读懂谁的方法？又想到什么问题？

师：谁看懂方法1了？

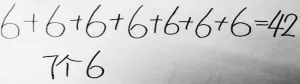
图2 （方法1）

生1：他的意思就是如果您忘记了6×7等于几，您可以想加法，7个6加起来是多少？也可以想：6个 7加起来是多少呢？这样就可以得出42。

师：也就是说6×7既可以表示6个7相加，也可以表示7个6相加。哪种方法表示的是6个7相加？

生2：方法2表示的就是6个7相加。如下图。

图3 （方法2）

生3：也可以画图，用下面的两种方法，数一数、算一算就知道了。

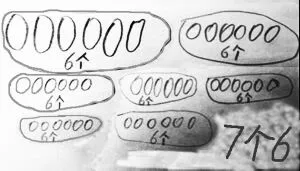
图4 （方法3）

图5 （方法4）

师：通过刚才的交流，你又想到新的问题了吗？

生4：我发现如果您忘记了乘法，就想加法，乘法和加法是一对好朋友。画图，也是可以的。

师：太感谢了！你们真会思考！继续看，方法5你能看懂吗？

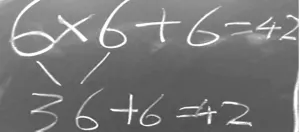
图6 （方法5）

生5：方法5说的是如果您忘记了6×7，就想6×6=36，再加上1个6就是42了。

师：方法6谁能看懂？如下图。

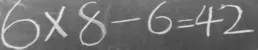
图7 （方法6）

生6：这种方法就是您如果记得6×8=48，再减掉1个6就可以了！大家有问题吗？

生7：为什么要减掉1个6呢？

生6：6×8表示8个6，老师忘记的是7个6，8个6减掉1个6就是7个6。

师：你们是利用口诀前一句与后一句之间的关系来解决问题的，对吗？

生：对！

师：方法7（如下图）是怎么想到的？谁给大家讲讲？

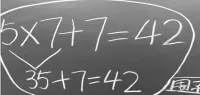
图8 （方法7）

生7：这个方法，是把 6个7，分成了5个7加1个7。

生8：其实还可以把6×7分成2个6加5个6。

生9:7个 6还可以变成 4个6加3个6。

师：我明白了，你们这样一分，就把新知识转化成了旧知识，可真了不起！如图9，这把尺子是做什么用的？

图9

生10：我明白，尺子上不仅有加法、减法，还有乘法口诀呢？一六得六，二六十二……六七四十二！

师：真是太神奇了！那我们看看，这么多方法，哪些方法是好朋友？哪些方法说的是同一件事儿？

生11：方法1和方法3，方法2和方法4，说的都是忘记了乘法，可以想到以前学的加法！

生12：还可以把新知识变成旧知识去解决。如方法5、方法6、方法7都是根据口诀的上一句和下一句之间的关系推出来的。

师：说得真清楚，推理在我们数学的学习中经常用到。点子图、数线，也是我们研究问题的好伙伴。谢谢大家为我出的好点子！

如何把学生的学习引向深入？借助教材中的问题串，我提出了引领性问题：“如果我忘记了6×7的结果是多少，你有什么好的办法吗？”引导学生深入理解乘法的意义，把之前停留在观察、分析、口头描述层面上的口诀引向深入，使学生系统、深入地思考口诀的意义，并尝试着建立起口诀之间的联系。引导学生通过多样化的方式表达自己的思考，将其思维外显化，从而提升学生思维的深度与广度。从“会背”到“会解释”，再到“会表达”，能提高学生不同层次的发展水平。

（作者单位：北京中关村第三小学）