基于AOTF成像光谱精密测量技术的研究

薛 鹏， 王志斌*， 张 瑞， 薛 锐， 赵同林

1. 电子测试技术重点实验室， 山西 太原 030051

2. 中北大学理学院， 山西 太原 030051

3. 山西省光电信息与仪器工程技术研究中心， 山西 太原 030051

基于AOTF成像光谱精密测量技术的研究

薛 鹏1, 2, 3， 王志斌1, 2, 3*， 张 瑞1, 3， 薛 锐2, 3， 赵同林1, 3

1. 电子测试技术重点实验室， 山西 太原 030051

2. 中北大学理学院， 山西 太原 030051

3. 山西省光电信息与仪器工程技术研究中心， 山西 太原 030051

声光可调滤波器(AOTF)作为光谱成像的一种新型分光元件， 在运用其进行成像光谱时， 一般选择入射光垂直于AOTF入射面时所对应的衍射中心波长为CCD的光谱测量波长。 但在实际测量中， 空间目标不同位置的光线总是以不同的角度进入到AOTF， 这样就导致了CCD实际测量的光谱和以光垂直入射时所对应的光谱为测量光谱相比出现误差， 影响了光谱的测量精度。 采用的成像光谱系统的特点是目标光线经前置光学系统、 AOTF和成像透镜后， 聚焦成像于透镜的焦平面上， 实现了目标光在整个系统的一次成像。 此一次成像与传统的二次成像相比， 能够有效的提高光能利用率和成像质量。 由于AOTF的视场角为±3°， 所以通过对AOTF视场角范围内衍射中心波长随入射角度变化的实际规律进行了分析研究， 并对衍射波长随入射角度变化的实际测量值进行了拟合修正， 得到了修正方程。 实验结果表明用修正后的方程进行光谱测量， 其相对误差值可以减小一个数量级。 此方法可为今后提高AOTF成像光谱测量精度奠定基础。

AOTF； 成像光谱； 光谱测量； 误差修正

引 言

声光可调滤波器(acousto-optic tunable filter, AOTF)是利用各向异性介质中的声光衍射原理制造的电调谐滤波器， 这种声光作用可用各向异性介质的反常布拉格衍射原理来解释。 AOTF分为共线和非共线两种类型， 实验所选用的是由材料TeO2制作的非共线[1]的AOTF， 其具有扫描速度快、 结构简单且无活动部件、 调谐范围宽、 衍射效率高等优点[2-3]， 因此目前基于AOTF的成像光谱[4-5]应用广泛。

任何物质都包含自身独特的光谱信息， 利用光谱成像技术可以对不同物体的光谱信息进行识别和分辨[6]。 光谱成像质量是成像光谱最重要的因素， 而光谱测量精度又在成像光谱测量技术中发挥着重要的作用。 在AOTF成像光谱实际研究中， 当光线入射角确定时， 某一驱动频率对应的某一固定的衍射光波长； 所以在一般光谱测量时选择的是以光垂直入射时所对应的这一固定衍射光波长为测量光谱。 但空间目标不同位置的光线不可能全部垂直进入AOTF， 这就导致了AOTF在±3°的视场角范围内光线入射角不同， 从而导致以不同角度入射的入射光其对应衍射光中心波长也发生变化[7]， 使得CCD不同位置探测到不同的光谱信息， 这就与只以光垂直入射时所对应的光谱为CCD测量光谱产生误差。 在追求高精度光谱测量的今天， 这种误差不能忽略。 所以， 为了最大限度的减小这种误差， 实验分别分析了在128和132 MHz的驱动频率下， 让一束平行光在AOTF入射面-3.5°～3.5°(以光垂直入射AOTF时为0°)范围内变化， 记录了一系列衍射中心波长随角度变化的实际数值， 得到了一个开口向上的抛物线方程， 并利用最小二乘法[8]对方程的开口系数进行了修正， 得到了修正后的方程。 用修正后的方程不但可以表示不同频率下衍射中心波长随角度变化的规律， 而且利用此方程进行光谱测量时， 还能大大的减小CCD进行光谱测量的误差， 提高了AOTF成像光谱的测量精度。

1 AOTF成像光谱

1.1 AOTF的工作原理

图1 AOTF的工作原理图

在满足动量匹配的条件下， 衍射光波长λ0与声速va、 声波频率fa、 入射光极角θi之间的关系如式(1)[9]

(1)

其中，no和ne分别为o光和e光的折射率， 当一束平行的复色光垂直入射到AOTF上时， 各种波长的单色光的入射角均为θ， 在声波频率fa确定以后， 由上式即可确定此驱动频率下所对应的衍射光的中心波长。

1.2 AOTF成像光谱光学系统

AOTF的成像光谱光学系统如图2， 空间目标与成像系统相距比较远， 所以目标每点发出的光可以近似的看成是平行光， 不同位置发出的光以不同的入射角度入射到前置光学系统， 平行光经前置光学系统后又以平行光的形式入射到AOTF中。 如空间某一点发出的光以α(-10°≤α≤10°)角入射到前置光学系统， 经前置光学系统后以β(-3°≤β≤3°)入射到AOTF中α>β。 前置光学系统压缩了入射光的入射角度， 从而保证了空间入射光能够进入到AOTF视场角可接受的范围内。 AOTF前后各有一个相互正交的偏振片[10]是为了滤掉0级非衍射光， 只要1级衍射光透射出来， 衍射平行光经成像透镜聚焦成像于CCD上。

图2 AOTF的成像光谱光学系统

从式(1)可知， 当va和fa固定以后， 衍射光的中心波长λ0随着入射光极角θi发生变化， 但实际中由于AOTF声光晶体加工工艺、 出射面光楔等因素的限制， 实际衍射光波长随角度的变化与理论式(1)上有一定的误差， 所以需要进一步实验来分析实际的衍射光波长随角度变化的规律。

2 AOTF成像光谱误差修正

2.1 实验分析

为了研究实际的衍射光中心波长随着入射角度变化的规律， 实验采用ABB公司研发的型号为SQG77000型复色光源(波长范围为400～1 000 nm)、 光阑、 JJY型1′分光仪(最小刻度为1′， 圆盘刻度为360°)、 中国电子科技集团公司第26所研发的LSGDN-3Z型AOTF(波长范围450～950 nm， 频率范围为220～65 MHz， 入射光孔径为8 mm×8 mm， 谱线宽度≤8 nm)、 Ocean optics HR4000-CG-UV-NIR型高分辨率光谱仪(光谱分辨率为0.2 nm@571.10 nm， 波长范围200～1 100 nm)， 光纤、 透镜等， 实验装置如图3。

图3 实验装置图

选取垂直入射为0°入射角， 让ABB光源发出的一束平行光通过转动分光仪来使其在AOTF入射面法线夹角的-3.5°～3.5°的范围内变化， 利用Ocean光谱仪记录下不同角度下衍射中心波长的变化的实际数值。 实验中分光仪每10′取一个值， 入射光分别在驱动频率为128和132 MHz下， 对应的衍射光中心波长随角度变化的实际数值如图4(a)和(b)， 从(a)和(b)可以看出在实际的衍射光波长随角度的变化趋势为开口向上、 对称轴为0的抛物线， 且越偏离垂直入射位置， 其波长变化越大， 即误差也就越大。

从图4(a)和(b)可以看出， 在128和132 MHz驱动频率下衍射光中心波长随角度变化的实际数值满足以开口向上的抛物线方程， 假设该方程为

(2)

其中λ为实际的随角度变化的衍射光波长，β为入射角，λ0(fa)为不同驱动频率下光线垂直入射到AOTF时所对应的衍射光中心波长，a为抛物线开口大小系数， 频率不同， 其开口大小不同。 所以对系数a进行修正可以得到不同频率下衍射波长随角度变化的规律。 表1为当光线垂直入射到AOTF时， 给定不同的驱动频率所对应的各自的衍射光中心波长。

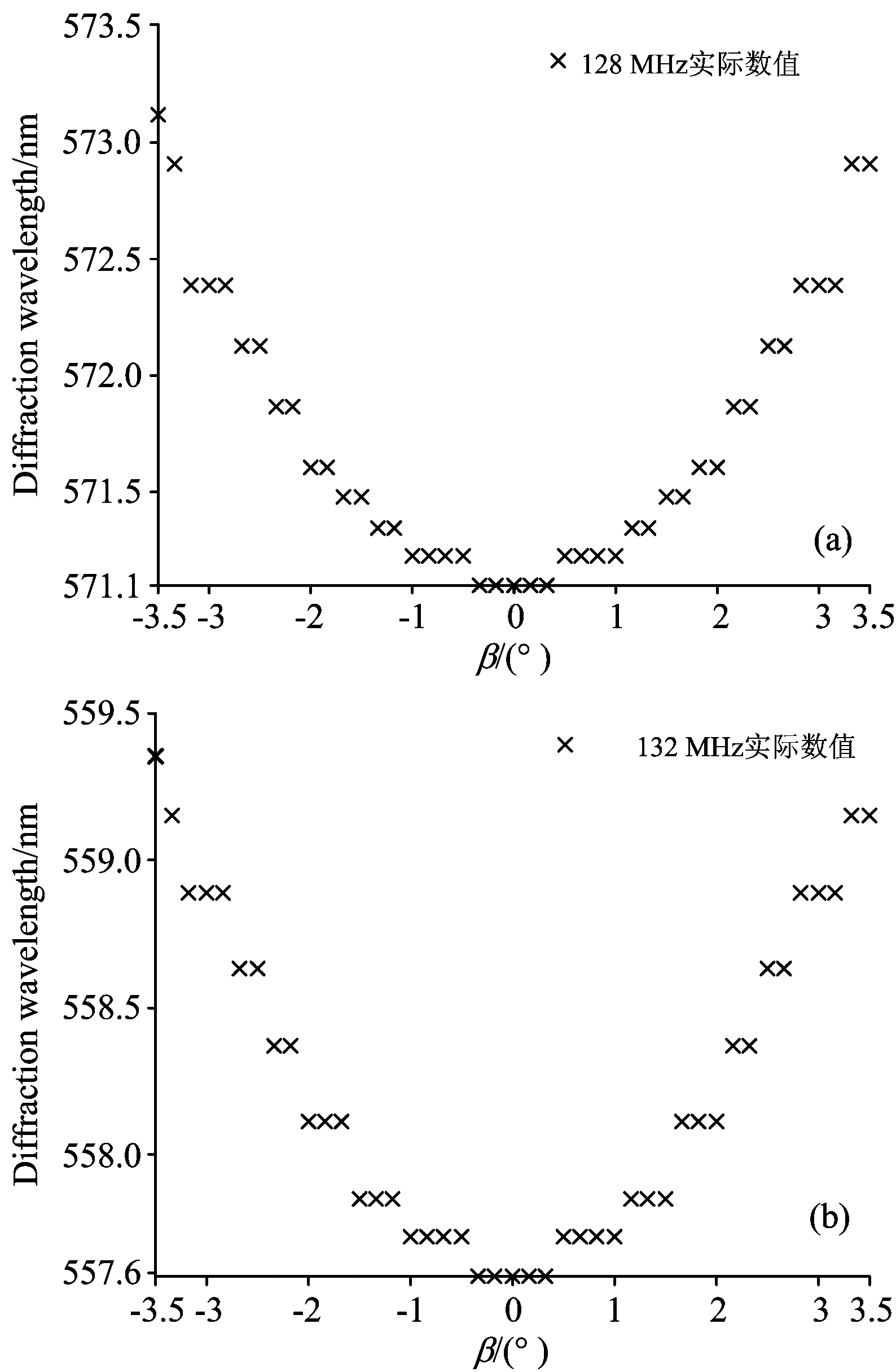
图4 衍射中心波长随角度变化的实际数值

Table 1 The diffraction center wavelength in different driving frequency when the light vertical incidence

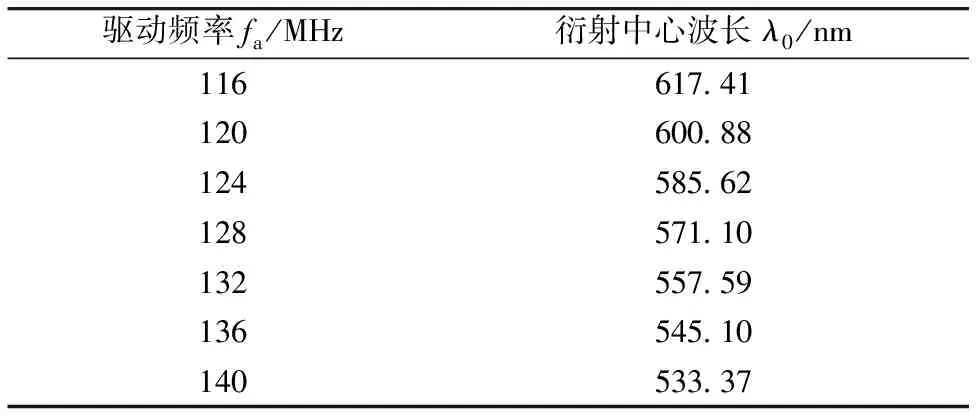
驱动频率fa/MHz衍射中心波长λ0/nm116617 41120600 88124585 62128571 10132557 59136545 10140533 37

2.2 AOTF成像光谱误差修正方法

通过实验发现不同入射角所对应的衍射光波长不同， 对CCD进行光谱测量时， 不同位置记录的光谱信息不同， 这就与一般以光垂直入射时的光谱为CCD的记录光谱时产生误差， 且偏离角度越大， 误差越大。 为了进一步表示不同驱动频率下衍射光波长随入射角变化的规律和减小测量误差， 用最小二乘法对方程(2)的系数a进行处理， 得拟合值与实际测量值偏差的平方和S为

(3)

其中λi为衍射波长的实际数值， 对a取偏导数为零来求得最佳的a值， 即

(4)

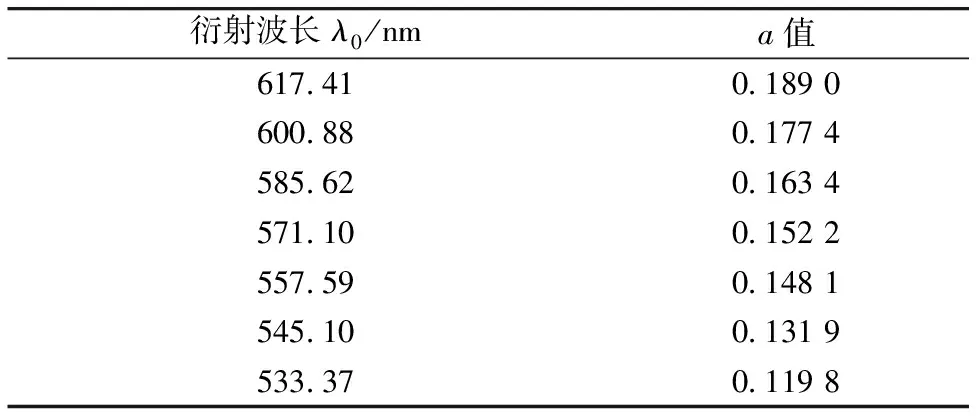
(5)

表2为不同衍射光波长λ0所对应的a值， 用最小二乘直线拟合对系数a值进行数值拟合， 其拟合图形如图5， 则a值随衍射波长λ0变化的直线方程为

a=0.000 802λ0(fa)-0.304 8

(6)

由式(2)和式(6)可得

(7)

图5 数值a随衍射波长λ0的变化

得到的式(7)为衍射光波长λ随入射角度β和驱动频率fa变化的函数关系式。 为了验证式(7)是否可以满足在不同驱动频率下衍射光中心波长随入射角度变化的一般规律， 图6(a)—(d)分别为式(7)在采用其他几种驱动频率下的可行性验证。

从图6可以看出， 修正后的式(7)衍射光波长随角度变化的数值与实际数值几乎能够吻合， 用修正后的方程来表示AOTF的测量光谱， 不仅测量方便， 而且与以光线垂直入射时的光谱为测量值相比， 其误差值大大的减小了。 所以， 修正后的式(7)不仅可以近似的表示在各种不同驱动频率下衍射波长与入射角变化的关系， 而且这种方法最大限度的减小了AOTF成像光谱的测量的误差， 提高了光谱测量的精度。

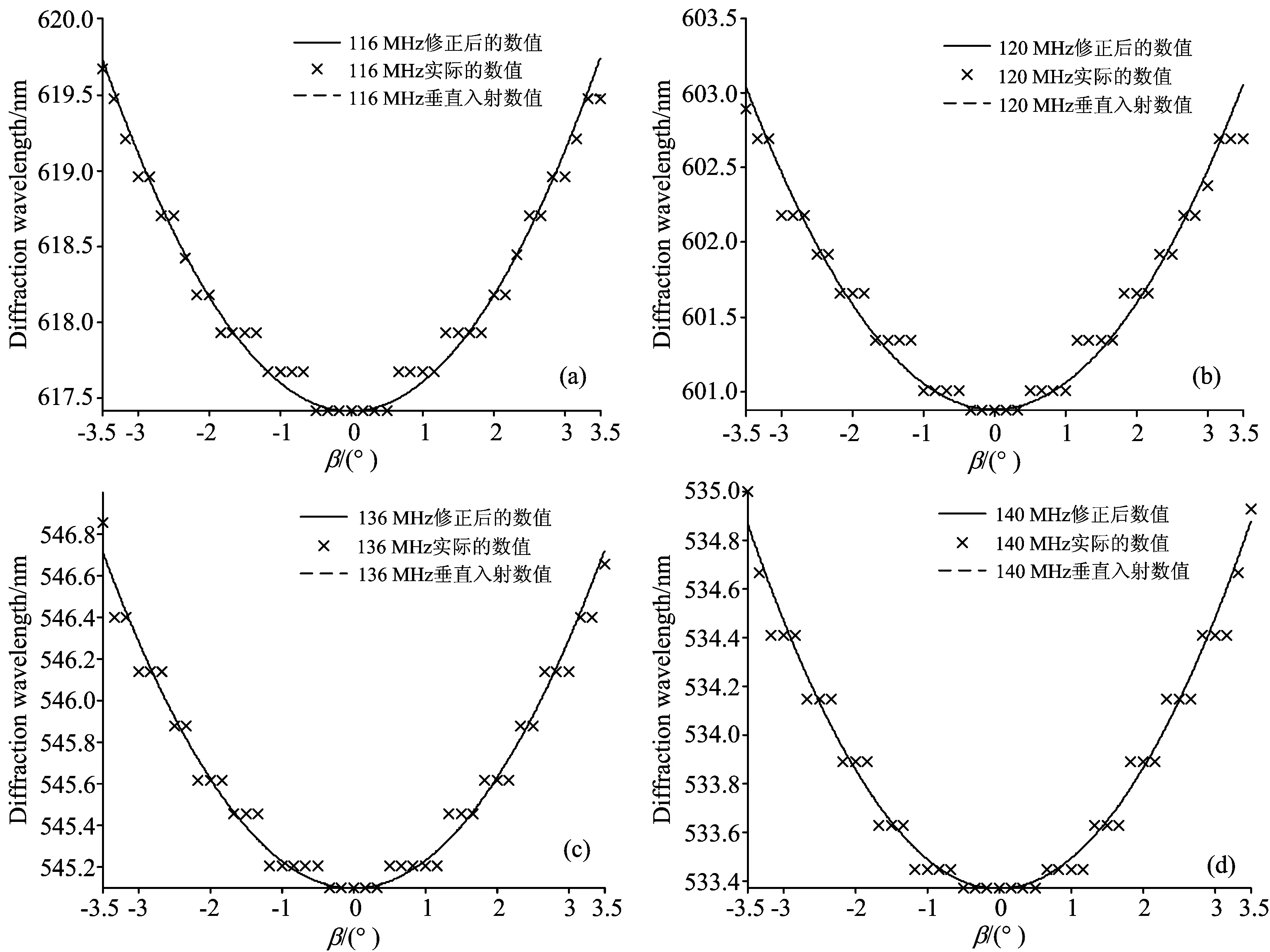
图6 修正后的各数值比较

2.3 相对误差计算

通过对128和132 MHZ驱动频率下衍射光波长随角度变化的实际规律进行分析研究以后， 得到了其变化的趋势方程， 并对趋势方程的系数进行了拟合修正， 得到修正后的方程。 该方程不仅可以满足不同频率下衍射光波长随角度的变化规律， 而且还大大的降低了CCD对AOTF成像光谱的测量误差。 通过对修正前后进行误差计算， 其中以光垂直入射时的光谱为测量光谱的相对误差值远大于以修正后式(7)得到的光谱为测量光谱时的相对误差， 即

(8)

其中λi为衍射波长的实际数值，λ0为垂直入射时的衍射波长，λ为修正后的衍射波长。 其不同频率下实际相对误差值与修正后的相对误差值如表3。

表3 不同衍射光波长下修正前后的相对误差值

Table 3 The relative errors before and after modification in different diffraction wavelength

衍射波长λ0/nm∑49i=1|λi-λ0|/λi∑49i=1|λi-λ|/λi617 411 1×10-31 1×10-4600 881 1×10-31 3×10-4585 621 0×10-31 1×10-4571 101 0×10-30 9×10-4557 591 0×10-30 9×10-4545 100 9×10-31 0×10-4533 370 8×10-30 9×10-4

从表3可以看出， 在不同的衍射波长λ0下， 修正后的误差比没修正以前的误差减小了约一个数量级。 所以对AOTF成像光谱测量进行修正以后， 大大的减小了测量误差， 为今后AOTF成像光谱的精确测量奠定了基础。

3 CCD像元与波长对应关系分析

空间目标的光线进入AOTF后， 只有水平方向不同角度的光线才会发生衍射波长的变化， 竖直方向不受影响， 而CCD每一个像元记录空间目标每一个点的光谱信息。 所以对于M×N像素大小的CCD成像来说， 而只有水平方向不同位置的像元记录不同的衍射光波长， 即记录了不同的光谱信息。 对于单个像元尺寸为d的CCD， 其CCD水平位置任一点像元所记录的光谱与光入射角的关系为

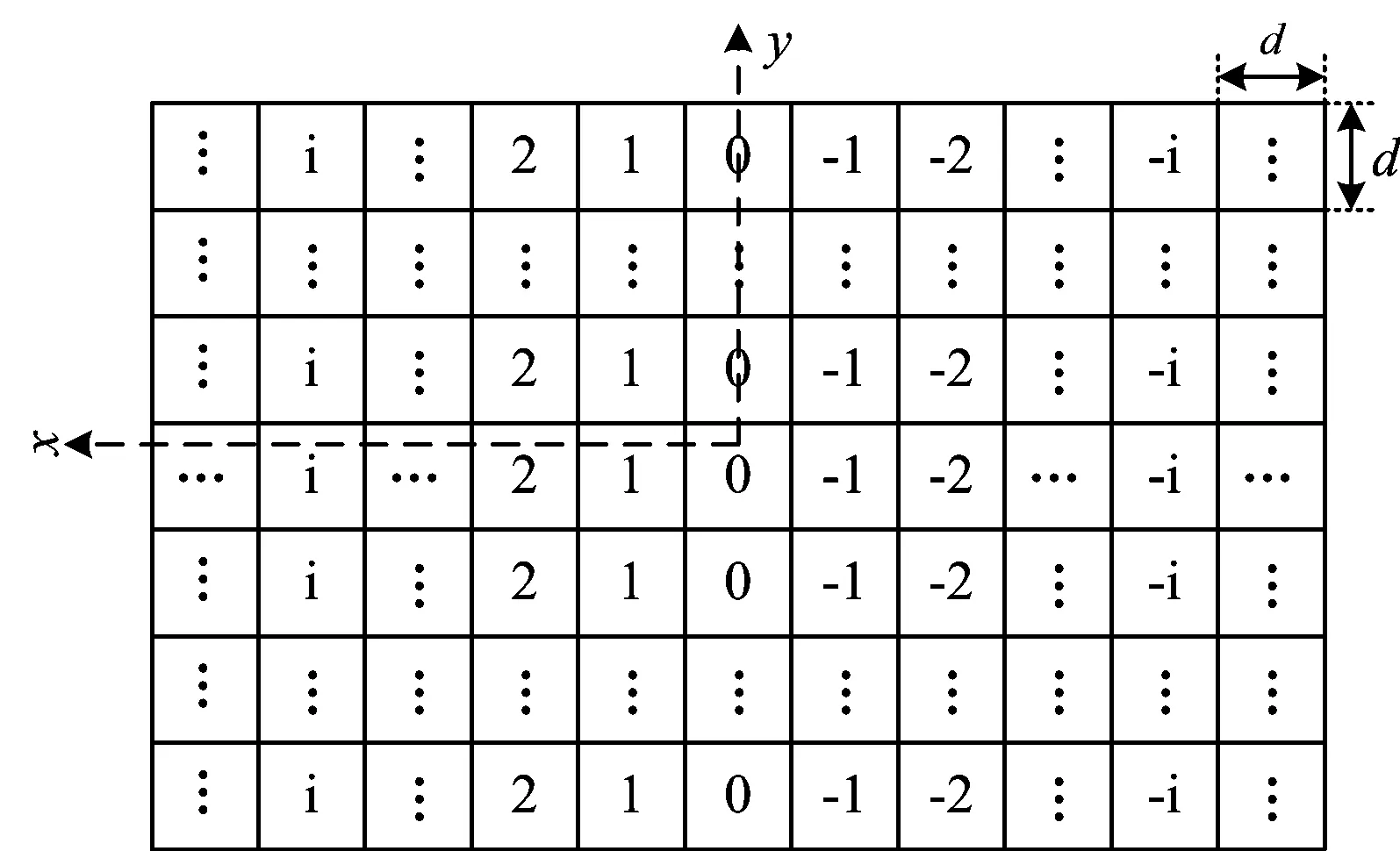
图7 CCD像面

(9)

其中f为成像透镜的焦距，ni为沿x方向距离CCD中心位置的第i个像元， 其CCD像面光谱信息如图7。

4 结 论

通过对一系列不同驱动频率下衍射光中心波长随角度变化的实验数据进行分析处理， 并根据变化规律得到了衍射波长随角度变化的拟合修正方程。 该方程不仅可以用来表示不同频率和不同角度的AOTF的衍射光中心波长， 而且与只以光垂直入射时的光谱为CCD测量光谱相比， 相对误差值降低了一个数量级， 大大的提高了AOTF成像光谱的测量精度。 该测量技术可以为今后AOTF进行光谱测量时提供一个理论基础。

[1] Gass P A, Sambles J R. Opt. Lett., 1991, 16(6): 429.

[2] Perchik A V. Proc. SPIE, 2013， 8888: 88880P.

[3] LIU Ji-fan, MA Yan-hua, ZHANG Lei(刘济帆， 马艳华， 张 雷). Infrared and Laser Engineering(红外与激光工程), 2013, 11(42): 3065.

[4] WANG Yao-li, ZHANG Rui, WANG Zhi-bin(王耀利， 张 瑞， 王志斌). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2015, 35(8): 2363.

[5] JIANG Yi, ZENG Li-bo, WU Qiong-shui(江 益， 曾立波， 吴琼水). Optical Technique(光学技术)， 2005， 31(2)： 193.

[6] Ward Farries M, Pannell C， et al. Proc. SPIE, 2010, 7835: 78350U.

[7] WANG Hao, HUANG Jun-feng, ZHANG Chun-guang(王 号， 黄俊峰， 张春光). Chinese Journal of Lasers(中国激光), 2015, 6(42): 0616003-3.

[8] ZHANG Xu-feng(张旭峰). The Experiment of College Physics(大学物理实验). Beijing: Mechanical Industry Press(北京： 机械工业出版社), 2013. 18.

[9] ZHANG Chun-guang, WANG Hao, QIU Yi-shen(张春光， 王 号， 邱怡申). Journal of Fujian Normal University(福建师范大学学报)， 2011， 27(6)： 45.

[10] LIU Kang, GAO Zhi-fan, WU Qiong-shui(刘 康， 高志帆， 吴琼水). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2015, 35(4): 1135.

The Study of Precision Measurement Technology Based on AOTF Imaging Spectrum

XUE Peng1, 2, 3, WANG Zhi-bin1, 2, 3*, ZHANG Rui1, 3， XUE Rui2, 3， ZHAO Tong-lin1, 3

1. Key Lab of Electronic Testing Technology, North University of China, Taiyuan 030051, China

2. College of Science, North University of China, Taiyuan 030051, China

3. Engineering Technology Research Center of Shanxi Province for Opto-Electronic Information and Instrument, Taiyuan 030051, China

Acousto-Optic Tunable Filter as a new beam splitting elements of spectral imaging. We often regard the diffraction center wavelength which is corresponded with the incident light perpendicular to the incident plane of AOTF as the wavelength of CCD spectral measurement. However, the different positions of target have different incident angles when the incident light enter into the AOTF, which will cause error when the CCD actual spectral measurement is compared with the spectral measurement of vertical incidence. The characteristics of this system we have used is that the target light imaging on the focal plane of CCD by passing the pre optical system， AOTF and the imaging lens, which have achieved the goal that the target light imaging on the whole system only once. Compared with the system of secondary imaging, the system of first imaging can improve the quality of image and the light energy utilization ratio. Because of the field angle of AOTF is ±3°, we analyzed the regular pattern of the diffraction wavelength changing with angle of incidence and obtained the revised spectrum measurement equation by processing the real measured value of diffraction wavelength changing with angle of incidence. The experimental results show that its relative error can be reduced an order of magnitude by using the revised equation to measure the spectrum. This method can lay the foundation for improving the measurement accuracy of AOTF imaging spectral in the future.

AOTF; Imaging spectrum; Spectral measurement; Error correction

Sep. 1, 2015; accepted Dec. 22, 2015)

2015-09-01，

2015-12-22

国家自然科学基金仪器专项基金项目(61127015)， 国际科技合作项目(2013DFR10150)和山西省青年科技研究基金项目(2014021012)资助

薛 鹏， 1991年生， 中北大学理学院硕士研究生 e-mail： xuepeng20062006@126.com *通讯联系人 e-mail： wangzhibin@nuc.edu.cn

O433.1

A

10.3964/j.issn.1000-0593(2016)08-2664-05

*Corresponding author