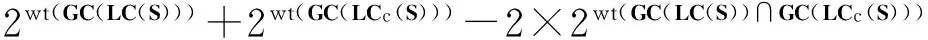二元序列的错误线性复杂度性质

常祖领, 　王　宁

(1.郑州大学 数学与统计学院　河南 郑州 450001; 2.福建师范大学 福建省网络安全与密码技术重点实验室　福建 福州 350007; 3.中原工学院 理学院　河南 郑州 450007)



二元序列的错误线性复杂度性质

常祖领1,2, 王宁3

(1.郑州大学 数学与统计学院河南 郑州 450001; 2.福建师范大学 福建省网络安全与密码技术重点实验室福建 福州 350007; 3.中原工学院 理学院河南 郑州 450007)

摘要：详细研究了二元2的幂次周期序列的错误线性复杂度的性质.利用Games-Chan算法作为基本工具，详细分析了2的幂次周期并且严格点少的二元序列的密码学性质.给出了具有两个严格点的序列的详细性质以及具有三个严格点的序列的结构.

关键词：二元序列； Games-Chan算法； 错误线性复杂度； 严格点

0引言

具有良好伪随机性的二元序列广泛应用于信息安全领域中[1—2].现在已经有很多用来度量序列的密码学性质的准则，二元序列S的线性复杂度，即能够生成该序列的线性移位寄存器的最小长度是最重要的准则之一[2].序列应具有较大的线性复杂度来抵抗根据Berlekamp-Massey算法[3]形成的攻击.对于周期为2n，n>0的二元序列，存在一个Games-Chan算法可以快速地计算出序列的线性复杂度[4]，并且这个算法的复杂度为O(N).

一个好的二元密码序列不仅要有较大的线性复杂度，当改变一些分量的值时，它的线性复杂度也不能降低太多.这就令研究者们引入了一个新的准则来衡量序列的密码学性质，即序列的k-错线性复杂度[5]，而序列的所有k-错线性复杂度以及对应的k组成的集合被称为序列的错误线性复杂度谱[6].文献[5]给出了一个对于任意k>0，可以快速计算二元2n周期序列的k-错线性复杂度的Stamp-Martin算法.文献[6]推广了Stamp-Martin算法能够快速计算出序列的所有k-错线性复杂度，从而求出错误线性复杂度谱.文献[7]给出了一个新的Stamp-Martin算法可以快速计算出为了使得序列的线性复杂度小于某个常数，必须改变原序列的分量值的个数k以及对应的位置.文献[8]中给出了只有两个严格点的二元2n周期序列的准确分类以及计数.文献[9]给出了二元2n周期序列的k-错线性复杂度严格小于线性复杂度时最小的k的确切值.

本文将研究二元2n周期序列的错误线性复杂度谱，特别是谱中某些特别的严格点的性质.对于具有两个严格点的二元序列，将给出这些序列的严格计数结果以及这些序列之间的关系.对于具有3个严格点的序列，将研究这些序列的结构，并说明这些序列其实是2个具有2个严格点的序列的模2和.本文还将给出一些错误线性复杂度谱的性质.

1基本概念

令S=s0,s1,s2,…表示一个二元序列，其中分量si取值于二元域F2={0,1}.如果存在一个正整数N满足si+N=si对所有非负整数i都成立，则称序列S具有周期N.这时设定S=(s0,s1,s2,…,sN-1).序列S的线性复杂度LC(S)定义为满足下面方程的最小正整数L,sj⊕d1sj-1⊕…⊕dLsj-L=0，对所有大于等于L的j都成立，其中系数d1,…,dL属于F2，并且⊕表示模2加.如果S为全零序列则线性复杂度为0，否则LC(S)就是能够生成该序列的线性移位反馈寄存器的最小长度[2].

Games-Chan算法[4]可以快速地计算二元2n周期序列的线性复杂度.

Games-Chan算法：

输入：S=SN=(s0,s1,s2,…,sN-1), N=2n, n>0;

输出：LC, S的线性复杂度.

LC=0; l=2n; i=0

whilel>1do

l=l/2; Si=(s0,s1,s2,…,s2l-1)

L=(s0,s1,…,sl-1), R=(sl,sl+1,…,s2l-1); Bi=L⊕R;

ifBi≠0/*这里0表示零序列

LC=LC+l; Si+1= Bi;

else

Si+1= L;

i=i+1;

endwhile

ifSn≠(0)thenLC=LC+1.

这个算法的某一次循环中，如果Bi≠0，一定有wt(Si-1)≥wt(Si)，这里wt(·)表示序列的汉明重量，即序列一个周期中1的个数.如果Bi=0，一定有wt(Si-1)=2wt(Si).如果序列S是非零序列，则在Games-Chan算法的最后一步中，一定有Sn≠(0)，所以线性复杂度一定会加1.这种情况下序列的线性复杂度可以表示为

LC(S)=a02n-1+a12n-2+…+an-221+an-120+1,ai∈F2,i=0,1,…,n-1,

其中ai=1当且仅当Bi≠0，序列的线性复杂度可以由ai的取值唯一确定.对于上面序列的线性复杂度的表示中，把向量(a0,a1,…,an-1)记为GC(LC(S))，称其为序列S的GC表示[10—11]，就是LC(S)-1的二进制表示.通过序列的线性复杂度LC(S)的GC表示，能很清楚地知道序列的Games-Chan算法的过程.序列的GC表示在本论文中会经常用到.

引理1[9]对于两个二元2n周期序列S1和S2，如果LC(S1)≠LC(S2)，则LC(S1⊕S2)=max{LC(S1), LC(S2)}；如果LC(S1)=LC(S2)，则LC(S1⊕S2)< LC(S1).

在文献[5]中Stamp和Martin定义了N周期二元序列SN=(s0,s1,s2,…,sN-1)的k-错线性复杂度LCk(S)等于在改变最多不超过k个S的分量的情况下能够获得的线性复杂度的最小值，即对于所有的满足0≤wt(EN) ≤k的N周期二元序列E，LCk(S)=minLC(S⊕E).如果一个序列E具有最小重量并且满足LCk(S)=minLC(S⊕E)，就称E为严格错误序列.

k=0时，LC0(S)=LC(S)，记为(0,LC(S)).随着k的增加，序列k-错线性复杂度会逐步降低.对一个可能的错误线性复杂度，取对应的最小的k构成二元组(k,LCk(S)).最后一个二元组应是(wt(S),0).把这些二元组构成的集合称为S的错误线性复杂度谱，而每个二元组称为序列S的错误线性复杂度谱的一个严格点[6].注意(0,LC(S))一定是序列的第1个严格点，而(wt(S),0)一定是最后一个严格点.本文主要研究具有2个或3个严格点的二元2n周期序列，记序列的第二个严格点为(c,LCc(S))，c表示序列的线性复杂度第一次降低时需要改变的分量的最小个数.

2只有两个严格点的序列的性质和计数

一个二元向量a=(a1,…,an), ai∈F2, 定义

对于序列的线性复杂度第一次降低时需要改变的分量的最小个数c，文献[9]和文献[10]给出了下面结果.

推论1令S为二元2n周期序列且LC(S)≠0，则S的每个周期的重量满足

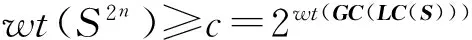
当且仅当S只有两个严格点等号成立.如果序列S的周期重量等于c，即序列S具有线性复杂度LC(S)且具有最小重量，则S仅有两个严格点(0,LC(S))和(c,0).令序列的线性复杂度的GC表示为GC(LC(S))= (a0,a1,…,an-1)，则在序列进行Games-Chan算法中一定会有

wt(Si)=21-aiwt(Si+1),i=0,1,…,n-1.

可以看出只有两个严格点的二元2n周期序列每个周期的重量就等于2b，其中b就是GC(LC(S))中0的个数，根据引理1，就可以直接推出定理1.

下面给出只有两个严格点的二元2n周期序列的个数的精确计数.

定理2只有两个严格点的线性复杂度为LC(S)并且GC(LC(S))=(a0,a1,…,an-1)的二元2n周期序列的个数等于

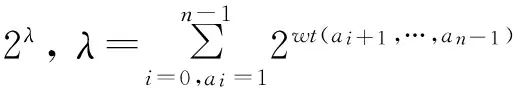
证明在对序列S进行Games-Chan算法时，考虑其中的结果：S0=S,S1, …,Sn=(1).如果an-1=1，则Sn-1有两种可能结果(01)和(10)；而如果an-1=0，则Sn-1只有一种可能(11).对于一般情况，当i从n-2到0时，如果ai=0，则Si左右两半相同且都是Si+1，所以wt(Si)=2wt(Si+1)，Si的可能个数与Si+1的可能个数相等,如果ai=1，则Si左右两半的和等于Si+1，所以wt(Si)=wt(Si+1)，而它们之间的个数关系为

其中N(·)表示序列的个数.根据上面的递归关系，可以证明这个定理.

只有两个严格点的二元2n周期序列具有很重要的应用.这样的序列一定是某个序列的严格错误序列.对于两个向量(或序列)a=(a1,…,an), b=(b1,…,bn),ai,bi∈F2，它们的交为

a∩b=(a1b1,…,anbn).

定理3令S1和S2为两个只有两个严格点的二元2n周期序列，则它们的交序列的周期重量满足

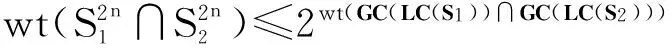
并且上界可达.

证明令这两个序列的线性复杂度的GC表示分别为:

GC(LC(S1))= (a0,…,an-1)，GC(LC(S2))= (b0,…,bn-1).

注意这两个序列都是具有对应线性复杂度的重量最小的序列.对它们分别进行Games-Chan算法，分别得到(S1)0=S1, (S1)1,…, (S1)n; (S2)0=S2, (S2)1,…, (S2)n.显然有(S1)n=(S2)n=(1).如果an-1=bn-1=0，则有(S1)n-1=(S2)n-1=(11)并且有

而如果an-1≠0或者bn-1≠0，则显然有

注意上式中等号是可以达到的.综上，无论何种情况，都有

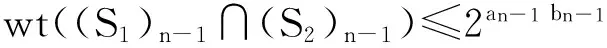
把这个分析推广到一般情形，则对i从n-1到0，当ai=bi=0时有

而当ai≠0或者bi≠0时有

并且式中等号是可以达到的.根据上面的分析可得

并且上界可达.

下面的推论说明任意二元2n周期序列，如果有必要的话，可以通过删除一些序列中的1,而使得最终序列具有同样的线性复杂度并且具有最小重量，即只具有两个严格点.

推论2令S为二元2n周期序列且LC(S)≠0，则存在一个具有同样的线性复杂度并且具有最小重量二元2n周期序列S′满足

S∩S′=S′.

3只有3个严格点的序列的结构

令序列的3个严格点分别是(0,LC(S))，(c,LCc(S))和(wt(S),0)，其中c等于定理1中的结果.下面定理说明这种序列都是2个只有2个严格点的二元2n周期序列的模2和.

定理4令S为二元2n周期序列且只有3个严格点(0,LC(S))，(c,LCc(S))和(wt(S),0)，其中c等于定理1中的结果.则S是两个二元2n周期，线性复杂度分别是LC(S)和LCc(S)的具有最小重量的序列的和，也就是说，这两个对应的序列只有两个严格点.另外，S的周期重量等于

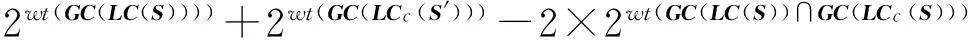
证明根据S的3个严格点和引理1及定理1，存在二元2n周期序列S1只有两个严格点(并且是同线性复杂度情况下重量最小的序列)满足LC(S1)=LC(S)以及LC(S⊕S1)= LCc(S)，此时序列S可以记做S=S1⊕(S⊕S1)=S1⊕S2，若S2不是只有2个严格点，则根据推论2，存在只有两个严格点的二元2n周期序列S′满足与S2有相同的线性复杂度，S2∩S′=S′并且S2≠S′.根据引理1，

LC(S2⊕S′)

所以S2⊕S′≠S1，从而

wt(S1⊕(S2⊕S′))>0，

由此可推出

wt(S1⊕S′)

并且

0≠LC(S⊕(S1⊕S′))< LCc(S).

从而推出序列S的严格点多于3个，引发矛盾.所以S2只有2个严格点.由此推出序列S是2个二元2n周期，线性复杂度分别是LC(S)和LCc(S)的具有最小重量的序列的和.

令S=S1⊕S2.如果

根据定理3，存在一个只有2个严格点线性复杂度等于LC(S2)的二元2n周期序列S′，使得

这样根据公式

wt(S1⊕S2)=wt(S1)+wt(S2)-2wt(S1∩S2),

可推出

wt(S1⊕S′)

再根据引理1

0≠LC(S⊕(S1⊕S′))

这也说明序列S的严格点多于3个，引发矛盾.综合上面分析即可推出S=S1⊕S2的周期重量等于

定理得证.

根据定理4的证明过程可以看出，并不是任意2个只有2个严格点的序列的和就是一个具有3个严格点的序列，还必须要求这2个序列的交的重量达到定理3中的上界才行.另外对于具有3个严格点的序列的3个严格点(0,LC(S)), (c,LCc(S))和(wt(S),0)中的LCc(S)也不是可以任意给定的.如果

根据定理4能够容易地推出如下推论.

推论3 令S是二元2n周期序列且至少有3个严格点(0,LC(S))，(c,LCc(S)), (d,LCd(S)), …, 则有

4结论

本文研究了具有较少严格点的二元2n周期序列的一些密码学性质，而Games-Chan算法是我们的主要工具.对于只有2个严格点的序列，推导出一些有意义的性质，包括它们的计数和交等性质.对于只有3个严格点的序列，本文研究了它们的结构，说明这些序列都是2个只有2个严格点序列的和的形式，并由此推出一些有意义的结果,这些结果在研究二元2n周期序列的密码学性质中有很好的应用价值.

参考文献：

[1]MENEZESAJ,OORSCGOTPC,VANSTONESA.Handbookofappliedcryptography[M].BocaRatonFL:CRCPress, 1996: 176—233.

[2]RUPPELRA.Analysisanddesignofstreamciphers[M].NewYork:Springer-Verlag, 1986: 133—200.

[3]MASSEYJL.ShiftregistersynthesisandBCHdecoding[J].IEEEtransactionsoninformationtheory, 1969, 15(1): 122—127.

[4]GAMESRA,CHANAH.Afastalgorithmfordeterminingthecomplexityofapseudo-randomsequencewithperiod2n[J].IEEEtransactionsoninformationtheory, 1983, 29(1): 144—146.

[5]STAMPM,MARTINCF.Analgorithmforthek-errorlinearcomplexityofbinarysequenceswithperiod2n[J].IEEEtransactionsoninformationtheory, 1993, 39(4): 1398—1401.

[6]LAUDERA,PATERSONK.Computingtheerrorlinearcomplexityspectrumofabinarysequenceofperiod2n[J].IEEEtransactionsoninformationtheory, 2003, 49(1): 273—280.

[7]SALAGEANA.Onthecomputationofthelinearcomplexityandthek-errorlinearcomplexityofbinarysequenceswithperiodapoweroftwo[J].IEEEtransactionsoninformationtheory, 2005, 51(3): 1145—1150.

[8]ETZIONT,KALOUPTSIDISTN,KOLOKOTRONISN,etal.Propertiesoftheerrorlinearcomplexityspectrum[J].IEEEtransactionsoninformationtheory, 2009, 55(10): 4681—4686.

[9]KUROSAWAK,SATOF,KISHIMOTOW.Arelationbetweenlinearcomplexityandk-errorlinearcomplexity[J].IEEEtransactionsoninformationtheory, 2000, 46(2): 694—698.

[10]CHANGZ,WENQ.Onthecryptographicpropertiesofbinary2n-periodicsequences[J].Chinesejournalofelectronics, 2011, 20(2): 307—311.

[11]CHANGZ,WANGX.Onthefirstandseconderrorlinearcomplexityofbinary2n-periodicsequences[J].Chinesejournalofelectronics, 2013, 22(1): 1—6.

(责任编辑：方惠敏)

Properties of Error Linear Complexity of Binary Sequences

CHANG Zuling1,2, WANG Ning3

(1.SchoolofMathematicsandStatistics,ZhengzhouUniversity,Zhengzhou450001,China;2.FujianProvincialKeyLaboratoryofNetworkSecurityandCryptology,FujianNormalUniversity,Fuzhou350007,China;3.CollegeofScience,ZhongyuanUniversityofTechnology,Zhengzhou450007,China)

Abstract:The properties of error linear complexity of binary sequences with period power of 2 were studied. With Games-chan algorithm as the main tool, the cryptographic properties of binary sequences with period power of 2 and few critical points were considered. The properties of sequences with two critical points and the structure of sequences with three critical points were provided.

Key words:Binary sequence; Games-Chan algorithm; error linear complexity; critical point

收稿日期:2015-09-17

基金项目:国家自然科学基金联合基金资助项目(u1301604)；河南省教育厅科学技术研究重点项目(14A110022);福建省网络安全与密码技术重点实验室(福建师范大学)开放课题(15005).

作者简介:常祖领(1976—), 男, 河南新乡人,副教授,博士, 主要从事密码学、编码理论以及序列的研究，E-mail: zuling_chang@zzu.edu.cn.

中图分类号：TN918.1

文献标志码：A

文章编号：1671-6841(2016)01-0032-05

DOI:10.3969/j.issn.1671-6841.201509016

引用文本: 常祖领, 王宁. 二元序列的错误线性复杂度性质[J]. 郑州大学学报(理学版)，2016，48(1)：32—36.