梁方程的一致紧吸引子

王素萍,　绍旭馗

(陇东学院 数学与统计学院　甘肃 庆阳 745000)



梁方程的一致紧吸引子

王素萍,绍旭馗

(陇东学院 数学与统计学院甘肃 庆阳 745000)

摘要：考虑了当外力项h满足条件C* (而非平移紧时)，利用一致条件(C)证明了非自治梁方程在强拓扑空间D(A)×V中一致吸引子的存在性.

关键词：梁方程； 一致条件(C)； 条件C*； 一致吸引子

0引言

文献[1—5]讨论了非线性梁方程强解及强全局吸引子的存在性，文献[6]讨论了梁方程在弱拓扑空间E0=V×H中指数吸引子存在性，在文献[7]中，作者只给出了非线性梁方程在弱拓扑空间E0=V×H中一致吸引子的存在性.假设Ω⊂R2是具有光滑边界∂Ω的有界区域.受以上研究及文献[8]的启发，本文将讨论下面非自治的梁方程:

utt+Δ2u+δut+λu+g(u)=h(x,t), (x,t)∈Ω×R+,

(1)

u(x,t)=Δu(x,t)=0,x∈∂Ω,t∈R+,

(2)

u(x,τ)=uτ(x),ut(x,τ)=pτ(x),x∈Ω.

(3)

在强拓扑空间E1=D(A)×V中一致紧吸引子的存在性.其中u(x,t)描述了桥面在竖直平面内的变形，h(x,t)和g(u)是外力项，δ>0表示黏性阻尼，λ>0.

假设非线性函数g满足下面条件:

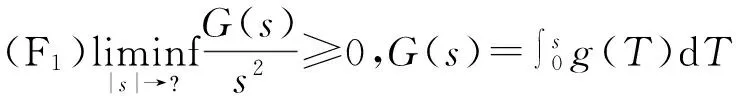
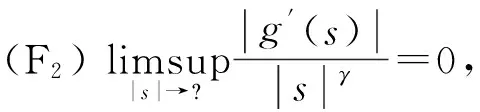
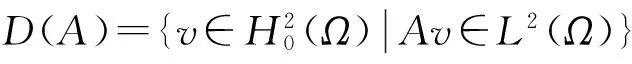
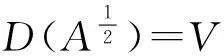
根据Poincare不等式，有

(4)

1 预备知识

定义2[10]过程族{Uσ(t,τ)}，σ∈Σ满足一致(关于σ∈Σ)条件(C)，如果对任意固定τ∈R，B∈B(E)和ε>0，存在t0=t0(τ,B,ε)≥τ和E的有限维子空间Em，使得:

其中dimEm=m和Pm:E→Em是一有界投影，记B(E)是E的所有有界子集的集合.

1)T(r)Σ=Σ,∀r∈R;2) 平移恒等性：Uσ(t+r,τ+r)=UT(r)σ(t,τ), ∀σ∈Σ,t≥τ,τ∈R,r≥0.

定理1[11]在假设I下，过程族{Uσ(t,τ)}，σ∈Σ有紧一致(关于σ∈Σ)吸引子AΣ，它满足AΣ=ω0,Σ(B0)=ωτ,Σ(B0),∀τ∈R如果它有：

1) 一致有界吸收集B0；

2) 满足一致条件(C).而且，如果E是一致凸的Banach空间，则逆也成立.

(5)

为方便起见,引进符号E0=V×H,E1=D(A)×V.

2E1中的一致吸引子

2.1 E1中的一致有界吸收集

用Av=Aut+ε0Au乘以(1)式在H中作内积

λε0‖u‖2+ ((g(u),Av))=(h(t),Av)，

(6)

由Hölder不等式及Young不等式,得

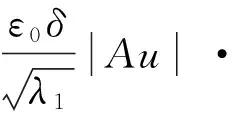
式中：x是d维设计变量，y(x)是目标函数，gi(x)是约束函数。当问题(1)的目标和约束函数值只能通过昂贵仿真得到时，通常借助代理模型以降低优化过程的仿真试验成本。

(7)

假设ε0足够小，使得

(8)

根据(F2)，定理2和Sobolev嵌入定理，有g(u)、g′(u)、g″(u)在L上是一致有界的，即存在K3>0，使得

(9)

结合Holder不等式，Cauchy 不等式有

(10)

结合(7)～(10)式，由(6)式得

(12)

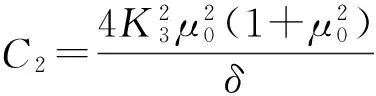
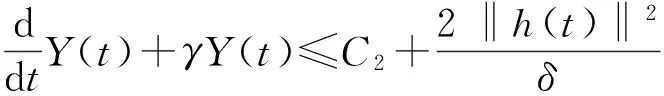
(13)

(14)

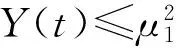
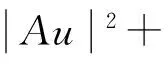
(15)

因此得到E1中的一致吸收集B1.

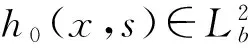
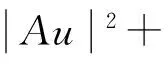
(16)

2.2 E1中的一致吸引子

引理2[1]设g∈C2(R,R),且满足(F2)，则g:D(A)且→V是紧连续的.

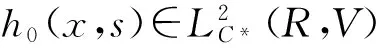
其中B1是E1中的一致(关于h∈H(h0))吸收集.

0<λ1≤λ2≤,…,λi→,i→，

且Aωi=λiωi，∀i∈N.记Gn=span{ω1,ω2,…,ωn},根据引理2，由于g:D(A)且→V是紧连续的，则对任意的ε>0，存在n>0,使得

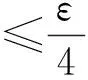
(17)

Qn:D(A)→Gn都是正交投影，对任意的(u,ut)∈E1,作如下分解，

(u,ut)=(u1,u1t)+(u2,u2t)，(u1,u1t)=(Qnu,Qnut).

取0<σ0<1，用Av2=Au2t+σ0Au2与方程(1)相乘，并在H中作内积可得

(18)

假若σ0足够小，使得

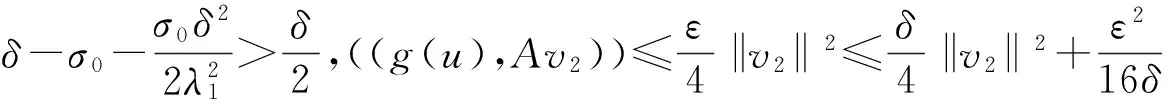
(19)

由(18)～(19)式有

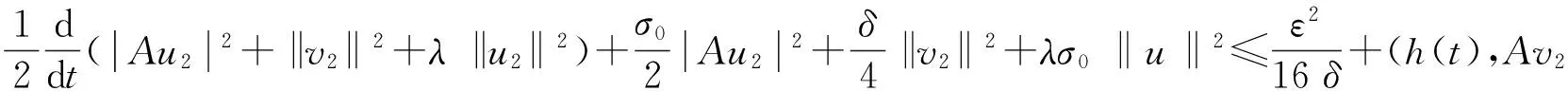
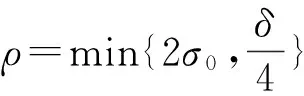
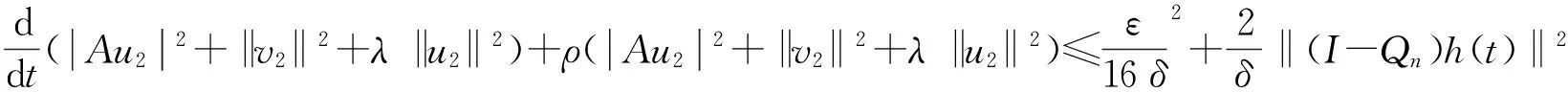
(20)

设

则有

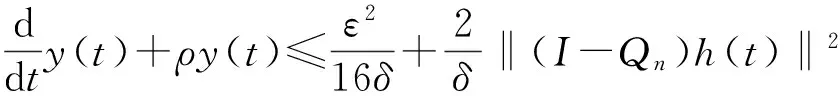
(21)

由Gronwall引理，得

(22)

由引理1，任意的ε1=ε1(ε)>0,存在足够大的n，使得

(23)

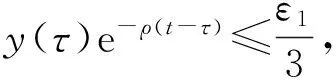
(24)

显然，可取ε1=ε1(ε),使得

(25)

再结合(23)～(25)式，得y(t)≤ε1, ∀t≥t2,h∈H(h0).这表明过程族{Uσ(t,τ)},h∈H(h0)在E1中关于h∈H(h0)满足一致条件(C).证毕.

参考文献：

[1]马巧珍,孙春友，钟承奎. 非线性梁方程强全局吸引子的存在性[J].数学物理学报，2007,27A(5)：941—948.

[2]MA Q Z, ZHONG C K. Existence of strong solutions and global attractors for the suspension bridge equations [J]. Nonlinear Anal, 2007,67:442.

[3]马巧珍，钟承奎. 吊桥方程全局吸引子的存在性[J].四川大学学报(自然科学版)，2006，42(2)：271.

[4]陈小豹，马巧珍.非线性可拉伸梁方程强全局吸引子的存在性[J]，西北师范大学学报(自然科学学报)，2008,44(6)：1—6.

[5] ROBISON J C.Infinite-Dimensional Dynamical Systems:An Introduction to Dissipative Parabolic PDEs and the Theory of Global Attractors[M].New York:Cambridge University Press,2001.

[6]王素萍，马巧珍，邵旭馗. 梁方程的指数吸引子[J].西南大学学报(自然科学版)，2011,33(9)：29—35.

[7]张晓明，姜金萍，董超雨. 非线性梁方程的一致吸引子[J].贵州师范大学学报(自然科学版)，2014,32(5)：76—81.

[8]MA Q Z,WANG S P,CHEN X B.Uniform compact attractors for the coupled suspension bridge equations[J]. Appl Math Comput,2011,217:6604—6615.

[9]CHEPYZHOV V V, VISHIK M I.Attractors for equations of mathematical physics [M].Providence RI：Colloquium Publications American Mathematical Society,2002.

[10]SU S S,WU H Q,ZHONG C K.Atrractors for non-autonomous 2D Navier-stokes equations with normal external forces [J].Discrete Contin Dyn Syst, 2005, 13: 701—709.

[11]MA S,ZHONG C K. The Attractors for weakly damped non-autonomous 2D Navier-stokes equations with normal external forces [J].Discrete Contin Dyn Syst, 2007,18:53—70.

(责任编辑：方惠敏)

Uniform Attractors for Beam Equation

WANG Suping,SHAO Xukui

(SchoolofMathematicalandStatistics,LongdongUniversity,QingYang745000,China)

Abstract:When forcing term only satisfies condition(C*), the existence of uniform attractors for the non-autonomous beam equations was proved in a strong topology space E1=D(A)×V by using the uniform condition (C).

Key words:beam equations; uniform condition(C);condition(C*);uniform attractors

收稿日期:2015-07-24

基金项目:甘肃省高等学校科研项目(2015A-147)；陇东学院青年科技创新项目(XYZK1401)．

作者简介:王素萍 (1980—), 女，甘肃镇原人，副教授，硕士,主要从事无穷维动力系统及偏微分方程的研究，E-mail:shwangsp@163.com.

中图分类号：O175.15

文献标志码：A

文章编号：1671-6841(2016)01-0027-05

DOI:10.3969/j.issn.1671-6841.201507039

引用本文：王素萍,绍旭馗.梁方程的一致紧吸引子[J].郑州大学学报(理学版)，2016,48(1)：27—31.