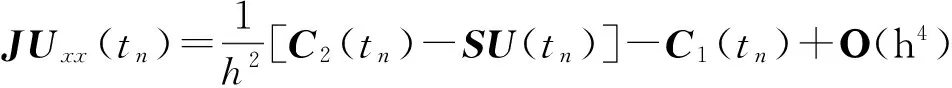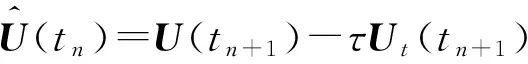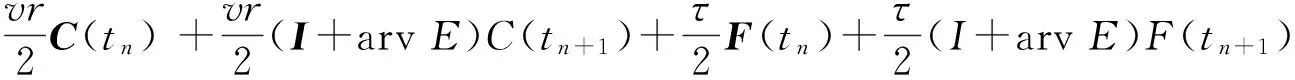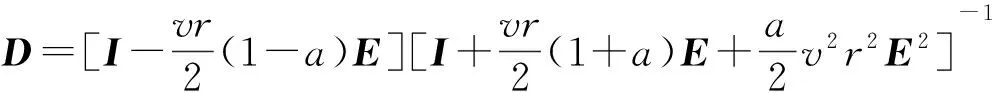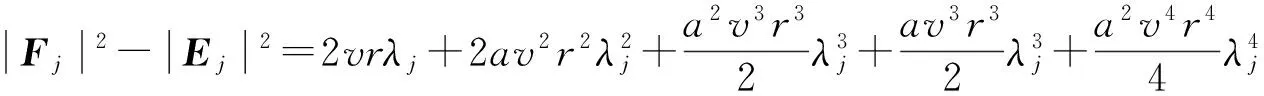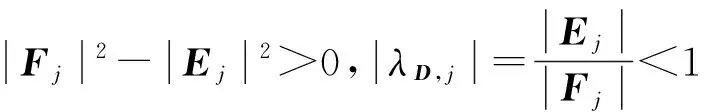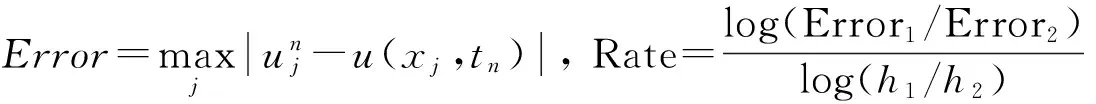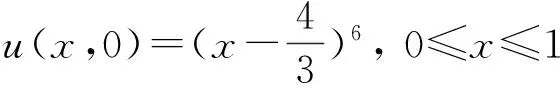求解一维扩散方程的一种高精度紧致差分方法

杨晓佳，　葛永斌

(宁夏大学 数学计算机学院　宁夏 银川 750021)



求解一维扩散方程的一种高精度紧致差分方法

杨晓佳，葛永斌

(宁夏大学 数学计算机学院宁夏 银川 750021)

摘要：针对一维扩散方程，空间采用四阶Padé 公式，时间采用广义的梯形公式，差分离散得到了一种时间二阶、空间四阶精度的隐式紧致差分格式，其截断误差为O(τ2+h4). 通过理论分析证明了此格式是无条件稳定的. 最后通过数值实验验证了格式的精确性和可靠性.

关键词：扩散方程； Padé 逼近； 紧致格式； 广义梯形公式； 稳定性

0引言

扩散方程是一类重要的抛物型微分方程，它在数学、物理、化学等领域都有着广泛的应用.自然环境、工程设备及生物机体中的许多物理现象都可用扩散方程来描述，由于物理问题本身的复杂性，其精确解往往不容易求得，因此研究其数值求解方法具有非常重要的意义.

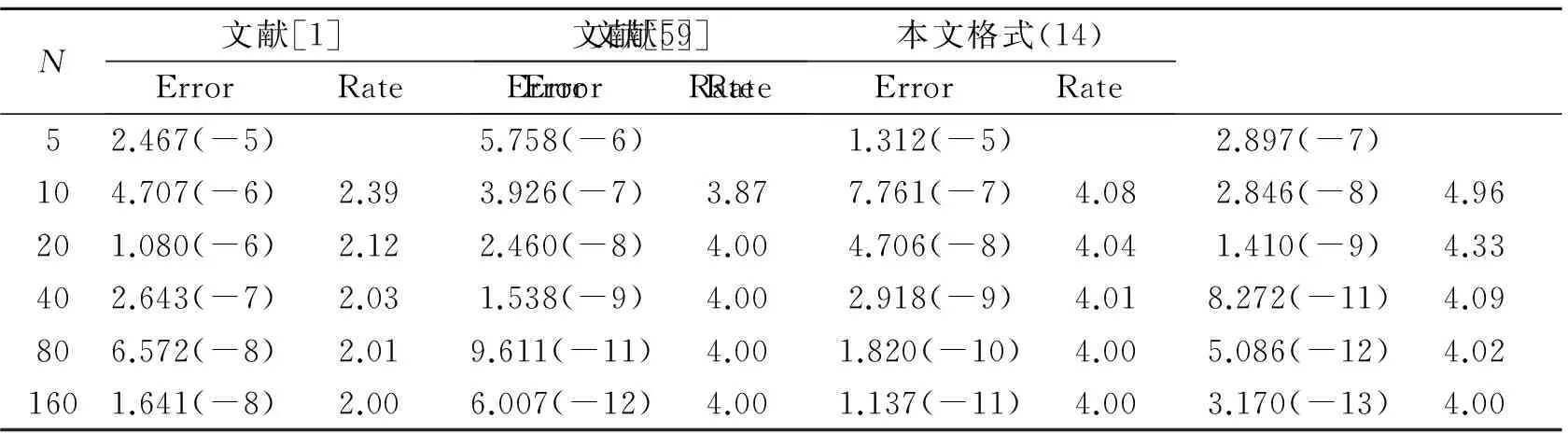
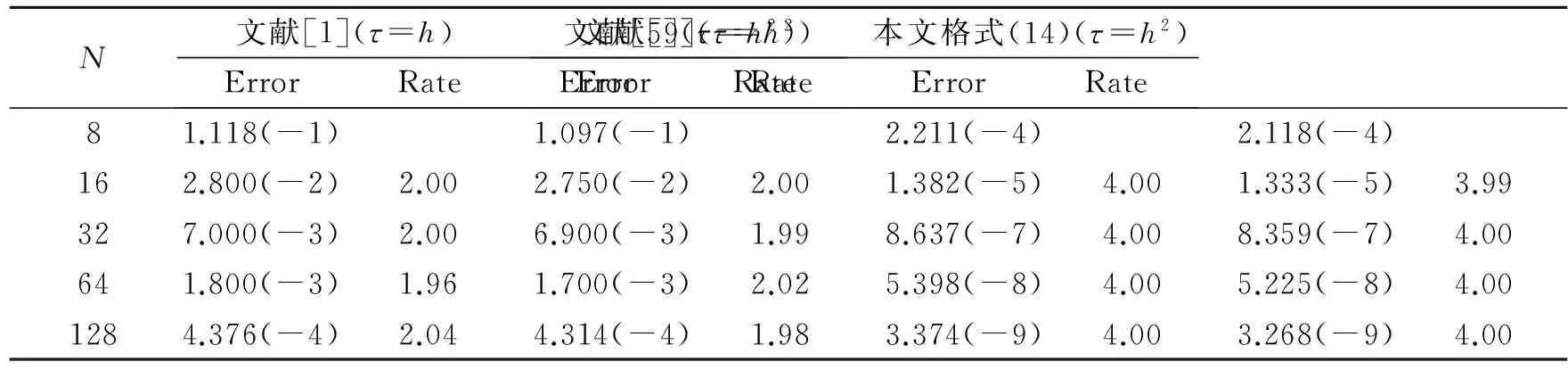
求解该问题的方法已有很多，如有限差分法、有限元法和有限体积法等.在有限差分法研究方面，近年来，已有大量研究工作.如文献[1]针对一维抛物型方程，采用中心差分格式将空间离散，得到一个关于时间t的半离散微分方程，然后采用广义的梯形公式离散微分方程，得到了一个截断误差为O(τ2+h2)的隐式紧致差分格式.文献[2]在离散关于时间t的半离散微分方程时采用了扩展的辛普森公式，得到了一个O(τ4+h2)的隐式紧致差分格式.文献[3]采用含参数差分方程逼近的方法,构造了一维齐次扩散方程的高精度隐格式，随参数选取的不同，格式的截断误差可分别达到O(τ2+h4)和O(τ4+h4)，但是O(τ4+h4)格式是无条件不稳定的. 文献[4]基于泰勒级数展开和待定系数的方法,构造了一维抛物型方程精度为O(τ3+h4)的3层3点显格式，其稳定性条件为r≤1/2(r为网格比)，即格式是条件稳定的.文献[5]利用一阶微商和二阶微商的四阶紧致差分逼近公式，推导出了求解一维扩散方程精度分别为O(τ2+h4)和O(τ4+h4)的两种隐式差分格式，其中O(τ2+h4)格式是2层无条件稳定的，而O(τ4+h4)格式是3层无条件不稳定的. 文献[6]提出了求解一维抛物型方程的一族2层6点隐式格式，格式的截断误差为O(τ2+h4)，并通过Fourier的方法证明了当1/2≤θ≤1(θ为参数)时，格式是无条件稳定的，当0≤θ<1/2，并且r≤1/6(1-2θ)，格式才是稳定的. 文献[7]采用区域分裂的方法，构造了一种求解一维和二维抛物型方程的高精度显格式，其截断误差为O(τ3+h3)，并且通过理论分析的方法证明其格式是无条件稳定的. 文献[8]对空间变量应用中心差分格式和紧致差分格式离散，时间变量采用二级四阶Runge-Kutta方法，构造了求解一维扩散方程的精度为O(τ4+h2)和O(τ4+h4)的两种无条件稳定的隐式差分格式. 文献[9]利用抛物型方程解的一阶偏导数在特殊节点处的一个差分近似式和二阶中心差商近似式，用待定系数法构造了一族隐式差分格式，格式的截断误差为O(τ3+h4)，稳定性条件为r>1/6. 文献[10]针对一维抛物型方程的初边值问题，采用待定系数法和泰勒级数展开的方法构造了一种2层8点隐式差分格式，其格式的截断误差为O(τ3+h5)，稳定性条件为0.001

1差分格式的建立

考虑一维含源项的扩散方程的初边值问题:

ut=vuxx+f(x,t), 00,

(1)

给定初始条件为:

u(x,0)=φ(x), 0≤x≤l,

(2)

给定边界条件为:

u(0,t)=a(t),u(l,t)=b(t),t>0,

(3)

其中：u(x,t)是待求未知函数；v(v>0)为扩散项系数；f(x,t)为非齐次项；a(t),b(t),φ(x)均为已知函数.

考虑在第n时刻的值，对空间内部节点采用四阶精度的Padé公式[11]逼近，则有

(4)

对于空间边界节点的处理，由式(1)与式(3)可得：

(5)

(6)

令

于是有

(7)

略去高阶项，(7)式可变形为

(8)

其中：E=J-1S;C(tn)=J-1[C2(tn)-h2C1(tn)].

由(1)式和(8)式可得

(9)

对时间方向的离散，采用广义梯形公式(GTF(a))[12]，有

(10)

(11)

将(9)式代入(10)式和(11)式可得：

(12)

(13)

将(12)式代入(13)式,整理可得

(14)

式(14)即为所构造的差分格式,通过对空间的离散过程不难发现，其具有四阶精度. 另外，由文献[1]的研究结论可知，时间具有二阶精度，因此本文所构造的差分格式(14)的截断误差为O(τ2+h4).

2稳定性分析

下面分析上述差分格式(14)的稳定性，假定边界条件精确满足，且右端项f无误差存在.

引理 1假设λ和x∈RN-1(x≠0)分别是矩阵J-1S的特征值和特征向量(J和S如上文定义)，则λ是实数且有λ>0.

证明由于λ和x分别是矩阵J-1S的特征值和特征向量，那么J-1Sx=λx⟹λxTJx=xTSx,令x=(x1,x2,…,xN-1)T,那么

所以xTSx>0， 而

则xTSx>0,由λxTJx=xTSx⟹λ>0，且λ为实数.

定理 1格式(14)是无条件稳定的.

证明令λj(j=1,2,…,N-1)是矩阵E的任意特征值，由引理1可知λj>0. 令

那么矩阵D的任意特征值为

记

则有

那么

因此，格式(14)是无条件稳定的.

3数值算例

为了验证本文所提格式的精确性和可靠性，现考虑如下4个带有精确解的问题，分别采用文献[1,2，5，9]和本文格式(14)进行了计算，给出了不同时刻、不同时间步长、不同空间步长以及不同网格比r的最大绝对误差及收敛阶，其中最大绝对误差及收敛阶定义如下：

Error1和Error2分别为空间网格步长为h1和h2时的最大绝对误差.

算例1[5]

ut=uxx, 00,

u(x,0)=sin(πx), 0≤x≤1,

u(0,t)=u(1,t)=0,t>0,

问题的精确解为u(x,t)=e-π2tsin(πx).

算例2[5]

ut=uxx+e-π2tsin(πx), 00,

u(x,0)=0, 0≤x≤1,

u(0,t)=u(1,t)=0,t>0,

问题的精确解为u(x,t)=te-π2tsin(πx).

算例3

算例4[1]

表1给出了问题1在t=1时对不同N的最大绝对误差及收敛阶，当问题1采用文献[1]和本文格式(14)计算时，均取a=0.3.从表1可以看出，文献[1]只有二阶精度，并且其最大绝对误差比本文格式的大几个数量级，而文献[5,9]和本文格式均具有四阶精度，但本文格式的最大绝对误差较文献[5,9]的最大绝对误差要小. 表2给出了N=32时，当网格比r分别为0.8、3.2、12.8、51.2时的最大绝对误差，可以看出格式(14)是稳定的，这与本文的理论分析结果是一致的. 表3给出了问题2在t=0.25时，对不同N的最大绝对误差及收敛阶，用文献[1]的方法和本文格式计算时，均取a=0.7.从表中的数值结果可以看出，本文格式比文献[1]和文献[5]的计算结果更为精确，并且当网格数逐渐增大时，本文格式的最大绝对误差要比文献[1]中的最大绝对误差小几个数量级. 表4给出了问题3的计算结果，该问题的边界是关于时间t的函数，从表4中的计算结果可以看出，在推导本文格式的过程中对边界条件的处理方法是切实可行的.对于该问题，用文献[1]的方法和本文格式计算时，均取a=0.2. 表5给出了当N=32时，问题4在t=5时，文献[1]、文献[2]、文献[5]和本文格式的数值解和精确解，在计算过程中，文献[1]和本文格式中取a=1/3，同样可以看出本文格式的计算结果较其他3个格式的计算结果更为精确. 表6给出了问题4当N=32时，当网格比r分别为0.8、3.2、12.8、51.2时的最大绝对误差，从表中的数值结果同样可知计算均是稳定的，这与本文的理论分析结果是一致的.

表1　问题1，当τ=h2,t=1时对不同N的最大绝对误差及收敛阶

表2　问题1，当N=32，t=0.5时对不同的r最大绝对误差

表3　问题2，在t=0.25时对不同N的最大绝对误差及收敛阶

表4　问题3，在t=1时对不同N的最大绝对误差及收敛阶

表5　问题4，当N=32,τ=h2，t=5时的数值解和精确解

表6　问题4 当N=32，t=1时对不同r的最大绝对误差

4结论

本文针对一维扩散方程提出了一种新的隐式高精度紧致差分格式，格式的截断误差为O(τ2+h4).通过理论分析证明了格式是无条件稳定的. 通过数值实验将本文格式与其他文献中的格式进行了比较，表明本文格式的计算结果更为精确，并且其精度和稳定性与理论分析结果相一致，从而验证了本文格式的精确性与可靠性. 虽然本文方法只是针对一维问题的，但是本文的方法可以直接推广到二维和三维，关于此方面的研究，我们将另文报道.

参考文献：

[1]CHAWLA M M, Al-ZANAIDI M A, EVANS D J. Generalized trapezoidal formulas for parabolic equations[J]. International journal of computer mathematics,1999,70(30)：429—443.

[2]SALLAM S, NAIM A M, ABDEL-AZIZ M R. Unconditionally stable C1-cubic spline collocation method for solving parabolic equations[J]. International journal of computer mathematics,2004,81(7): 813—821.

[3]周顺兴. 解抛物型偏微分方程的高精度差分格式[J]. 计算数学,1982,4(2): 204—213.

[4]马明书. 一维抛物型方程的一个新的高精度显式差分格式[J]. 数值计算与计算机应用,2001,22(2): 156—160.

[5]葛永斌, 田振夫, 詹咏,等. 求解扩散方程的一种高精度隐式差分方法[J]. 上海理工大学学报,2005,27(2): 107—112.

[6]詹涌强. 求解抛物型方程的一族六点隐式差分格式[J]. 安徽大学学报(自然科学版),2012,36(4): 26—29.

[7]WEN R H, SHAO H Z. Domain decomposition schemes with high-order accuracy and unconditional stability[J]. Applied mathematics and computation,2013,219(11): 6170—6181.

[8]开依沙尔热合曼, 努尔买买提黑力力. 求解扩散方程的二级四阶隐式Runge-Kutta方法[J]. 湖北大学学报(自然科学版), 2014, 36(5): 476—480.

[9]詹涌强, 张传林. 解抛物型方程的一族高精度隐式差分格式[J]. 应用数学和力学, 2014, 35(7): 790—797.

[10]周敏, 高学军, 董超. 解抛物型方程的八点隐式差分格式[J]. 广东工业大学学报(自然科学版), 2014, 31(4): 71—78.

[11]LELE S K. Compact finite difference schemes with spectral-like resolution[J]. Journal of computational physics,1992,103(1): 16—42.

[12]CHAWLA M M, Al-ZANAIDI M A, EVANS D J. A class of generalized trapezoidal formulas for the numercal integration of y′=f(x,y)[J]. International journal of computer mathematics, 1996, 62(1/2):131—142.

(责任编辑：方惠敏)

A High-order Compact Difference Method for the One-dimensional Diffusion Equation

YANG Xiaojia , GE Yongbin

(CollegeofMathematicsandComputerScience,NingxiaUniversity,Yinchuan750021,China)

Abstract:For the one dimensional diffusion equation, a high-order compact difference scheme was constructed by using the fourth-order Padé formula for space discretization and the generalized trapezoidal formula for time discretization, and the truncation error of the scheme was O(τ2+h4). The unconditional stability of the scheme was analyzed by theoritical method. Numerical experiments were carried out to verify the accuracy and the reliability of the present method.

Key words:diffusion equation; Padé approximation; compact scheme; generalized trapezoidal formula ; stability

收稿日期:2015-06-28

基金项目:国家自然科学基金资助项目(11361045, 11161036)；宁夏高等学校科学技术研究项目(NGY2013019).

作者简介:杨晓佳(1988—)，女，宁夏吴忠人，硕士研究生，主要从事偏微分方程数值解法研究，E-mail：yang_xiaoj@sina.com；通信作者：葛永斌(1975—)，男，宁夏吴忠人，教授，博士生导师，主要从事偏微分方程数值解法研究，E-mail：gyb@nxu.edu.cn.

中图分类号：O241.82

文献标志码：A

文章编号：1671-6841(2016)01-0010-07

DOI:10.3969/j.issn.1671-6841.201506013

引用本文：杨晓佳，葛永斌. 求解一维扩散方程的一种高精度紧致差分方法[J]. 郑州大学学报(理学版)，2016，48(1)：10—16.