基于AHP法对单兵火箭弹弹丸炸点精度影响因素的分析改进

丁　玮,洪　黎,宋　彬

(1.南京理工大学，南京　210094；2.中航工业航空动力控制系统研究所，江苏 无锡　214161)



基于AHP法对单兵火箭弹弹丸炸点精度影响因素的分析改进

丁玮1,洪黎2,宋彬1

(1.南京理工大学，南京210094；2.中航工业航空动力控制系统研究所，江苏 无锡214161)

摘要：单兵火箭弹的炸点精度在很大程度上决定了其毁伤效果，因此对炸点精度的研究至关重要。炸点精度受整个武器系统的影响，所以只有从武器系统角度才能对弹丸炸点精度作全面分析。从系统角度分析了影响弹丸炸点定距精度的一些因素，并对主要影响因素利用AHP法建立了基于武器系统的弹丸炸点精度分配模型，计算出各影响因素的精度权重，同时以炸点定距精度系统指标±10 m为例进行了各影响因素的精度分配。最后对炸点精度影响因素进行了仿真分析，并结合武器系统精度分配结果对不满足系统精度分配指标的影响因素提出相应的改进措施，从而使系统炸点精度得到进一步提高。

关键词：AHP法；定距精度；精度权重；仿真

进入21世纪以来，由于世界形势和作战对象的变化，反恐战争、特种部队作战、地区性局部冲突己经成为重要的战争形式。单兵火箭弹由于体积小、质量轻、携带方便，非常适合这些作战模式[1-3]。

单兵火箭弹在爆炸威力一定的条件下，它的爆炸效果主要由单兵火箭弹的炸点精度决定，而影响单兵火箭弹炸点精度因素包括初速、 射角、 地面温度、 风向与风速等等，因而要想对单兵火箭弹的炸点精度进行更好的改进，必须要从武器系统的角度出发，这样才能使弹丸炸点精度得到更加全面的分析。因此本研究首先较为全面地分析并总结出其中一些对弹丸炸点精度造成影响的因素，利用AHP法建立弹丸炸点精度分配模型，对影响弹丸精度的主要因素进行仿真分析，将仿真结果与精度分配模型进行对比，对没有达到系统精度分配指标的影响因素提出相应的整改方案。

1炸点精度影响因素

炸点精度是单兵火箭弹对目标命中能力的度量。炸点精度又称定距误差，它用目标或瞄准点到弹着点的矢径表示，它是一随机变量。炸点精度由定距准确度和定距密集度组成[4]。下面分别从定距准确度和定距密集度两个方面分别对影响炸点精度的因素进行分析。

1.1定距准确度的影响因素

武器系统的定距准确度用平均弹着点与瞄准点的偏差度量，它是定距精度的重要组成部分，用目标到平均弹着点的矢径表示，由一系列系统误差引起[5]。

影响定距准确度的因素包括发射筒与目标的几何系统误差，气象、弹药和武器系统的系统误差，它主要来源于测量误差、弹道准备误差、气象准备误差等，具体参见表1所示。

表1　定距准确度各误差因素

测地误差和目标位置误差可以做到很小，是可以控制的，在此不作考虑；弹道准备误差主要可体现在发射筒对弹丸的初速上；气象准备误差即弹道环境包括温度、湿度、风速、气压是不可控的，需要对其进行分析，甚至进行相应修正；技术准备误差主要涉及瞄具系统误差；其他误差主要体现在引信误差，包括测速误差以及修正方法的系统误差等。因此可从弹丸初速、气象因素(包括温度、湿度、风速、气压等)、激光瞄具、引信等方面来计算和分析弹丸定距准确度。

1.2定距密集度的影响因素

定距密集度是火箭弹的重要战术技术性能参数，也是定距精度的重要组成部分，它用平均弹着点到弹着点的矢径表示，是由一系列微小随机误差引起的，影响定距密集度的因素众多，各影响因素如表2所示。

火药性能、装药结构、点火传火、药室、筒身、弹重、弹炮摩擦、膛压等可综合反映在发射筒对弹丸射角、初速、章动的影响上，即体现在发射筒的精度；装定射击诸元、瞄准的微小差异主要体现在激光瞄具的精度上；测速误差以及修正方法误差，装定误差、电池激活误差、定时误差、发火电路误差是引信定距精度的6个因素；气象方面的气温、气压、风速、风向的微小变化同样给定距密集度带来影响；其他一些微小随机变化，可反映在弹丸章动和弹形、质量、转动惯量等参数上，因此可从发射筒、激光瞄具、引信、气象环境、弹丸这5个方面的分析和计算弹丸的定距密集度。

表2　定距密集度各影响因素

2基于AHP法各影响因素的精度分配

从上面影响因素分析知，单兵火箭弹炸点定距精度主要受发射筒、弹丸、引信、激光瞄具和气象环境等方面的影响，考虑到这些因素的可控性和控制的难易程度使用AHP法对它们进行精度指标分配。

2.1AHP法的基本步骤

AHP法的基本流程是首先对问题进行分析，了解问题所包含因素之间的关联关系和隶属关系，根据各因素的关系建立层次结构模型，依据判断矩阵规则建立该层次的判断矩阵，进而使用一致矩阵法对建立的判断矩阵进行一致性检验，如果不通过一致性检验，需重新修正判断矩阵，直到通过一致性检验。通过一致性检验后，最终使用单层次权重分配计算方法对该层次的所有因素进行权重分配[6-10]。

其中一致性检验方法为：首先求出待检验矩阵的最大特征量λ，再根据式(1)求出一致性指标CI，然后根据矩阵维数查表3得到随机一致性指标RI，通过式(2)求得一致性比率CR，若CR<0.1时，认为待检验矩阵的不一致程度在容许范围之内，有满意的一致性，通过一致性检验，否则，不通过一致性检验[11-12]。

(1)

(2)

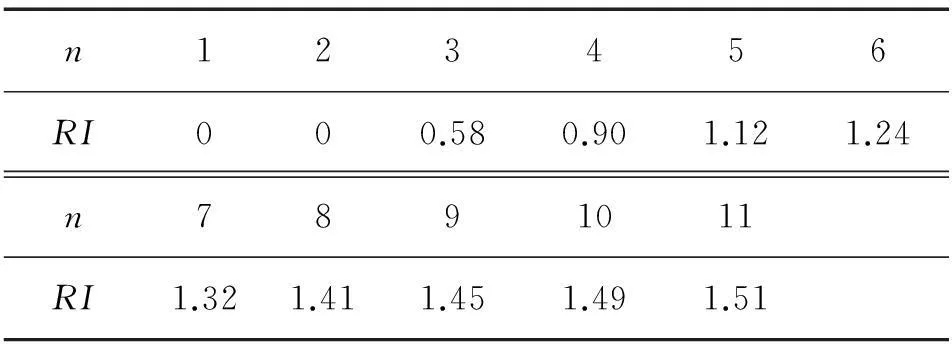
表3　随机一致性指标 RI

其次单层次权重分配计算方法为：首先构造单层次的判断矩阵A，根据式(3)由判断矩阵A计算出中间矩阵B，进而根据式(2)计算出最优传递矩阵C，再进而由矩阵C根据式(3)计算出拟优一致矩阵d，根据方根法求出矩阵d的特征向量和特征值，找到最大特征值所对应特征向量的列，将此列值均除以此列所有值的和，求得的结果即为对应的权重值[13]。

(3)

(4)

(5)

2.2建立层次结构模型

根据精度因素建立结构模型，如图1所示，弹丸引信的定距精度A与引信C1、激光瞄具C2、炮管C3、弹丸C4、气象环境C55个方面有关，首先对A-C建立第一层次关系；然后对这5个方面的内部各因素分别建立第二层次关系，其中影响定距精度的引信方面因素有：测速误差、测速修正误差、计时误差、电池激活误差、装定误差、发火电路误差，即构成引信(C1)层；影响定距精度的激光瞄具方面因素有探测器灵敏度、信号发生电路带宽、逻辑控制电路处理速度，即构成激光瞄具(C2)层；影响定距精度的炮管方面的因素有：射角误差、初速误差、章动，即构成炮管(C3)层；影响定距精度的弹丸方面的因素有：弹形、质量、章动、转动惯量，即构成弹丸(C4)层；影响定距精度的气象环境方面的因素有：空气压力、空气湿度、温度、风速等，即构成气象环境(C5)层[14]。而本研究中所讨论的单兵火箭弹具有自测速功能，因此高低温变化对初速跳动的影响很小，基本不对炸点精度造成误差，所以温度在此对系统造成的直接影响可不予考虑。

图1　迫击炮、弹及基本药管作用原理示意图

2.3构造判断矩阵并计算

在确定各层次各因素之间的权重时，如果只是定性的结果，则常常不容易被别人接受，因而Santy等人提出一致矩阵法，即：

演出前，我在心里默念着，一定要唱好每一句歌词，记得每一个调度，做好每一个动作，不能出现意外和失误。经过努力，这一切我们真的全都做到了！

1)不把所有因素放在一起比较，而是两两相互比较；

2)采用相对尺度，以尽可能减少性质不同的诸因素相互比较的困难，以提高准确度。

判断矩阵的元素Aij用Santy的1～9标度方法给出，具体含义如表4所示。

表4　1～9尺度Aij的含义

下面以第一层次为例，即定距精度(A)-5个方面(C)层，构造判断矩阵，其余层次判断矩阵构造方法与之一致，故不再赘述。

建立判断矩阵A0，相对于引信精度、激光瞄具精度、炮管精度、气象环境精度，弹丸精度最易控制，所以以其作为比较标准。而从控制难度来说依次为引信层、激光瞄具层、炮管层、气象环境层、弹丸层。

计算得到最大特征量为5.009 3，根据式(1)求得一致性指标CI为0.002 325，通过查表3知随机一致性指标RI为1.12，那么一致性比率CR=0.002 325/1.12=0.002 1<0.1，所以通过一致性检验。

WC1=0.428 4，WC2=0.246 8，WC3=0.063 4，

WC4=0.130 7，WC5=0.130 7。

2.4精度分配

依次将其余层次的判断矩阵按上述方法构造出，并将各分配的权重结果整理如图2所示[14]。

进一步根据两层权重结果计算得到5个方面具体影响因素占整个系统精度的权重，并将结果整理成表5，由于环境因素中的几个因素权重大小视具体情况而定，在此作为一个整体考虑，不作具体分配。

假设弹丸精度为±10 m进行分配举例，分配结果如表6所示。

图2　精度分配权重

系统精度AC1C2C3C4C50.42840.24680.06340.13070.1307P1P2P3P4P5P6P7P8P9P10P11P12P13P14P15P160.53310.18320.10900.05820.05820.05820.53960.29700.16340.59170.33320.07510.57350.30230.06210.0621P17～P19

表6　系统精度为±10 m时精度分配

3各影响因素对弹丸炸点精度的影响分析

由于本单兵火箭弹为微旋弹，所以章动变化、转动惯量变化对炸点的影响可以忽略，在此不作考虑。现有激光瞄具在600 m位置处精度可达到±2 m[15]，可满足系统分配指标，在此不作分析，而引信中电池激活误差、装定误差、发火电路的作用时间误差近似认为为0，所以对炸点的影响可以忽略，同样不作分析。

在其他参数为标准条件下，将射程分析至600 m，分别对测速、计时、测速修正、射角、弹形系数、质量变化、空气压力、温度、风速这些影响因素在各自的变化下分别进行了仿真分析，并将仿真数据整合统一成表7所示。

表7　各影响因素在各自变化下定距点的定距精度

对比表6和表7知:测速精度、计时、测速修正、射角、弹性系数、弹丸质量、湿度这些影响因素在各自的变化范围内对定距精度所造成的误差均满足系统分配指标要求，故不再做进一步研究；而空气压力和风速的变化对系统所造成的射程误差则超出了系统分配指标，因此需要对这两个影响因素进行修正，以提高系统炸点精度。针对空气压力这一影响因素，可在本文中所研究的单兵火箭弹的弹箭头部加装阻力环装置，便可利用弹载控制系统和探测系统实现弹箭向预定弹道上逼近，从而减小散布，大幅度提高弹箭射击精度，继而达到提高系统定距精度的目的[16]；对于风速这一影响因素，可在该单兵火箭弹上安装智能风速修正测控系统。该系统由风速检测和智能控制两部分组成。风速检测是在风杯风速仪的基础上利用光电传感器进行检测，光电传感器排列成半圆形阵列，机械装置指针的不同指向使光电传感器阵列输出不同的电压信号。智能控制部分采用灰色预测算法对测量结果进行智能处理以及灰色预测，借助 PID 控制算法对火箭弹炮瞄准系统进行延时控制，修正了火箭弹在横风作用情况下的落点偏差，并使火箭弹发射系统的瞄准修正时间大大缩短，从而改善火箭弹发射系统的性能[17]。

4试验验证

为考察上述理论分析结论的正误，针对某单兵火箭弹进行了靶场动态试验，重点分析按上述精度分配方法设计下，弹丸炸点精度能否满足系统指标要求。

4.1试验过程

图3为试验场景布置示意图。首先激光测距机测得目标距离，将目标信息传输给装定器，装定器将目标信息经过处理后装定给待发射弹丸的引信，同时在传输信息之前将能量传输给引信电容电源存储起来，弹丸发射后，一方面引信经过测速磁铁时进行弹载自主测速，进而根据测得的速度和经过装定器处理后的目标信息，依照上述选定的测速修正方法对引信的作用时间进行修正，从而得到修正后的引信作用时间，另一方面当弹丸经过天幕靶时，天幕靶将弹丸的炮口速度测量并且记录下来，最终引信根据修正后的作用时间引爆弹丸。同时，测风仪将弹丸发射时刻的风速和风向记录下来，以便于对引信炸点定距精度进行分析。

图3　试验场景布置示意图

4.2试验结果分析

空炸试验结果如表8和表9所示：由于试验时风速风向变化不大，故在此不考虑风速对弹丸精度的影响。试验共发射10发火箭弹，10发弹丸均定距在400 m位置处空炸，5发未测速修正弹丸结果如表8所示，5发加测速修正弹丸结果如表9所示。

通过上面试验结果可看出：5发未测速修正引信炸点均值396.44 m，标准差为12.34，总体散布在±5 m范围的概率为0.34；5发测速修正引信炸点均值399.48 m，标准差为2.25，总体散布在±5 m范围的概率为0.97，说明测速修正引信系统炸点精度较高，能够满足系统指标±10 m的要求。试验结果表明：文中精度分配与改进措施有效，能够满足系统对炸点精度的要求。

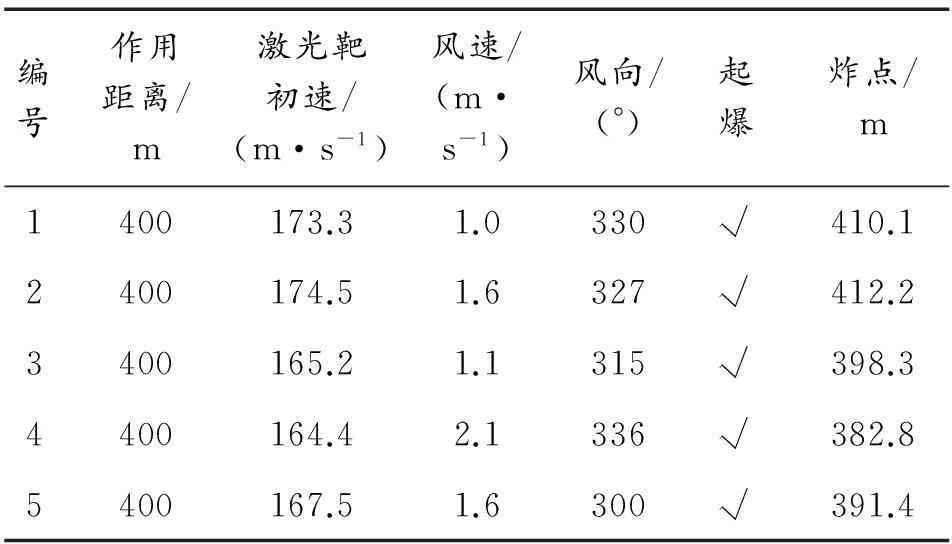
表8　未测速修正弹丸试验结果

表9　测速修正弹丸试验结果

5结论

本研究主要介绍了单兵火箭弹基于AHP分析方法，从系统角度出发对武器系统各影响因素进行了精度分配，同时将各影响因素对弹丸炸点精度的影响进行了仿真分析，把仿真结果和系统分配指标进行比较，对没有达到系统精度分配指标要求的一些影响因素进行更深层次的研究，并给出相应的改进方案，使得弹丸炸点精度得到进一步的提高。本文的研究成果对于提高单兵火箭弹弹丸炸点精度具有非常重要的意义,可使单兵火箭弹在实际作战中的命中率得到很大的提高。

参考文献：

[1]贠来峰,芮筱亭,陈涛.一种平衡抛射单兵反装甲武器发射装药低温发射安全性分析[J].兵工学报,2010(4):429-433.

[2]贠来峰,芮筱亭,冯可华.平衡抛射武器内弹道性能研究[J].南京理工大学学报(自然科学版),2009(2):258-261.

[3]隋高山.单兵火箭新型发射原理初步研究[D].南京：南京理工大学,2009.

[4]郭锡福.远程火炮武器系统射击精度分析[M].北京：国防工业出版社，2004.

[5]刘利生，吴斌，吴正容，等.外弹道测量精度分析与评定[M].北京：国防工业出版社，2009.

[6]李金芳.基于AHP/DEA的20 kV中压配电方案研究及评估[D].北京:华北电力大学，2009.

[7]许树柏.层次分析法原理[M].天津：天津大学出版社，2003.

[8]岳麓，潘郁.动态层次分析法在客户关系管理系统中的应用[J].南京工业大学学报，2004,26(5)：81-86.

[9]张管飞，陈进宝.基于AHP 的导弹武器系统效能模糊综合评估[J].四川兵工学报，2011,32(1):58-61.

[10]黄世国.基于模糊层次分析法的建筑企业安全管理评价[J].重庆工学院学报(自然科学)，2009,23(3):52-55.

[11]王敬，陈志武.武器系统综合能力的 AHP 群决策评价[J].火力与指挥控制，2012,37(10):182-184.

[12]李国友，张成，刘宪臣.导弹部队信息作战能力的模糊综合评估[J].战术导弹技术，2007(4):36-39.

[13]陈达，贾慧，李海涛.基于AHP的航空导弹武器系统效能分析[J].仪器仪表用户杂志，2007,14(1):101-102.

[14]马少杰.小口径空炸引信炸点精度和可靠性分析技术研究[D].南京:南京理工大学，2006.

[15]崔鹏，史学舜，陈坤峰，等.基于光电延时法的激光测距精度测试系统[J].宇航计测技术，2011,31(1):57-61.

[16]王中原,史金光.一维弹道修正弹气动布局与修正能力研究[J].南京理工大学学报(自然科学版),2008(3):333-336.

[17]童敏明,黄艳,徐剑坤.火箭炮射向的智能风速修正测控系统[J].火炮发射与控制学报,2007(2):52-55.

(责任编辑周江川)

本文引用格式：丁玮,洪黎,宋彬.基于AHP法对单兵火箭弹弹丸炸点精度影响因素的分析改进[J].兵器装备工程学报，2016(5):29-35.

Citation format:DING Wei，HONG Li，SONG Bin.Analysis and Improvement of Factors Affecting the Accuracy of Burst Point of an Individual Rocket Based on AHP Method[J].Journal of Ordnance Equipment Engineering,2016(5):29-35.

Analysis and Improvement of Factors Affecting the Accuracy of Burst Point of an Individual Rocket Based on AHP Method

DING Wei1，HONG Li2，SONG Bin1

(1.Nanjing University of Science and Technology,Nanjing,210094,China; 2.AVIC Aviation Motor Control System Institute,Wuxi 214161,China)

Abstract:The accuracy of burst point of an individual rocket determines the damage effect largely,so its study is very important.The accuracy of burst point is affected by the whole weapon system,so only from the perspective of the weapon system,can we make a comprehensive analysis of the accuracy of burst point.First of all,this paper not only analyzed some factors affecting the accuracy of burst point from the perspective of system,but also established the accuracy allocation model of projectile burst point on weapon system and calculated the weight of each factor by using AHP method,in addition,this paper gave the accuracy allocation by the example of a ±10 m.Finally,the influencing factors of the accuracy of burst point were analyzed in the simulation,and this paper put forward a number of corresponding improving measures to some factors which can’t meet the requirements of the system,so as to make the accuracy of burst point of the system better.

Key words:AHP method; distance precision; precision weight; simulation

doi:【装备理论与装备技术】10.11809/scbgxb2016.05.008

收稿日期：2015-11-09；修回日期：2015-12-10

作者简介：丁玮(1990—),男,硕士研究生,主要从事通信与电子工程研究。

中图分类号：TJ415

文献标识码：A

文章编号：2096-2304(2016)05-0029-07