一种基于谱分析的非带限卫星信号信噪比估计算法

易　辉，侯孝民，马　宏，吴　涛

(装备学院，北京　101416)



一种基于谱分析的非带限卫星信号信噪比估计算法

易辉，侯孝民，马宏，吴涛

(装备学院，北京101416)

摘要：为了实现对非带限卫星信号信噪比的快速高精度估计，分析了传统的基于谱分析的信噪比估计算法的对非带限卫星信号估计不准的原因，提出了一种新的基于谱分析的信噪比估计算法；该方法利用主瓣范围内信号功率与信号总功率之比和主瓣范围内噪声功率与噪声总功率之比求得信号功率和噪声功率，从而得出信噪比；对BPSK和QPSK信号的仿真结果表明：新算法性能稳定，可有效提高估计精度，在-10～10 dB的范围内，估计的偏差和均方根误差基本都小于0.5 dB；提出的新的基于谱分析的信噪比估计算法可用于各种调制方式，计算复杂度小，可以满足对非带限卫星信号信噪比估计的需求。

关键词：信噪比估计；谱分析；非带限；卫星信号

信噪比(SNR，Signal to Noise Ratio)是衡量卫星通信信号品质的重要指标之一。对于某一种调制方式，信噪比与误码率有着直接对应的关系[1]，通过估计接收信号的信噪比，可以有效监测接收信号的信号品质，为信号解调提供重要参考依据。此外，在通信系统中，很多环节都需要信噪比的先验知识优化通信性能，如自适应调制系统中调制和编码方式的选择，移动通信网络中的越区切换、码分多址系统中的功率控制[2-3]等等。

根据是否需要辅助数据，信噪比估计算法可以分为数据辅助类算法(DA:Data-aided)和非数据辅助类算法(NDA:Non Data-aided)两类。DA估计算法准确性较高，但是需要牺牲信道传输效率为代价。NDA方法在系统正常传输信息数据的同时进行信噪比估计，不影响信息传输效率，适用范围较广。

常用的信噪比估计算法有最大似然估计法(ML)[4-5]、分离符号矩算法(SSME)[6-7]、二阶矩四阶矩估计算法(M2M4)[8-9]、子空间估计算法[10-11]和基于功率谱的估计算法[3,12]。最大似然估计法精度高，但需要周期地发送训练序列，运算复杂，是一种DA算法；分离符号矩算法只能对判决域信号进行处理，是一种NDA算法；二阶矩四阶矩估计算法是基于统计量的NDA算法，其估计随着观测数据的增加会越来越接近真实值；子空间估计算法在高信噪比的情况下性能较好，在低信噪比情况下性能下降，且其运算量较大，是一种NDA算法；基于谱分析的估计算法可以用FFT快速实现，运算量少，复杂度低，且不需要辅助数据，是一种NDA算法，在工程上应用广泛。

卫星通信通常呈现出信噪比低，数据量大的特点，要实现对接收卫星信号的实时监测和准确估计，基于谱分析的信噪比估计算法是一种可选方案。但是，对于非带限的卫星信号，传统的基于谱分析的估计算法存在缺陷。文章通过分析传统算法的不足，提出一种新算法，通过利用主瓣范围内信号功率与信号总功率之比和主瓣范围内噪声功率与噪声总功率之比来求得信号功率和噪声功率，从而改善了基于谱分析的信噪比估计算法对非带限卫星信号信噪比估计的性能。

1传统的基于谱分析的信噪比估计算法

传统的基于谱分析的信噪比估计算法[2,3,12]对白噪声信道下的带限信号有较好的适用性。白噪声信道下的接收信号中，噪声功率谱均匀分布在整个观测频带内，而带限信号的功率谱只在有限的频带范围内存在。利用这一特性，先对接收到的时域信号进行功率谱估计，根据功率谱估计出信号的频带范围，将信号范围外的功率谱当作噪声谱，计算信号范围外的噪声谱的均值作为噪声功率谱密度的估计值。然后用噪声功率谱密度乘以观测带宽得到噪声功率，用接收信号总功率减去噪声功率得到信号功率，两者相比就可以得到SNR估计值。

假设以 fS采样率对接收信号进行采样，得接收信号

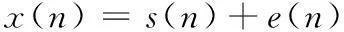
(1)

其中，S(N)为发送信号，E(N)为方差为σ2的零均值白噪声。对离散信号x(N)进行功率谱估计，得到接收信号的功率谱

(2)

其中，Px(f)表示接收信号的功率谱，PS(f)表示信号的功率谱，PE(f)表示噪声功率谱。由于正负功率谱对称，因此只需计算正半轴。

假设接收信号功率谱的正半轴如图 1所示，虚线以下表示理想白噪声的功率谱，虚线以上表示带限信号的功率谱。经过估计得到带限信号频带范围为[fL,fH]，根据信号频带范围外的功率谱可以估计出噪声功率谱密度：

(3)

从而可以估计出信噪比：

(4)

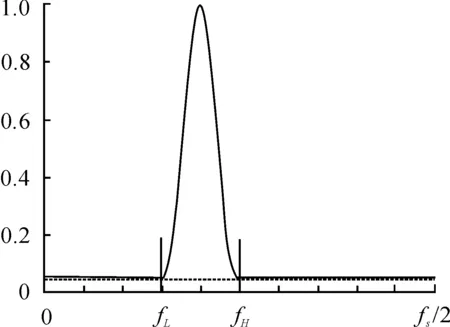
图1　带限信号功率谱图

基于谱分析的估计算法的关键在于估计信号的频带范围。文献[2]中提出了一种利用平均功率谱密度单调性求频带范围的方法，在频带边缘下降陡峭时效果较好，在频带边缘下降缓慢时会带来误差。对于带限信号，求出有误差的频带范围后，将频带范围适当放宽就可以较好地将信号限制在估计的频带范围内，从而估计带外的噪声功率谱密度。对于非带限信号，为了准确估计带外的噪声功率谱密度，需要准确地估计信号的频带范围，而非带限信号的旁瓣相对主瓣较小，幅度下降也比较缓慢，再用上述方法估计频带范围时会带来较大误差。此外，这种方法较为复杂，计算量较大。

对于非带限信号，另一种简单的做法是将信号的主瓣(无噪声情况下的第一过零点)作为信号的频带范围，把主瓣外的旁瓣信号当成噪声处理，这是一种有偏估计。这种做法虽然简单，但也会像文献[2]方法那样带来误差，甚至误差会超过文献[2]。这种做法在信噪比较低时，可以对接收信号的信噪比进行近似估计，但是当信噪比较高时，将会带来较大的误差。

通过分析可以发现，传统算法之所以对非带限信号估计性能不好，是因为在计算噪声功率谱密度的时候，没有准确估计信号频带范围，将部分信号功率当作了噪声功率进行计算，这就导致估计出来的噪声功率偏大，而信号功率偏小，最终导致信噪比估计值比真实值偏小。

2新的基于谱分析的信噪比估计算法

针对传统的基于谱分析的估计算法对非带限信号估计不准的问题，提出一种新的基于谱分析的信噪比估计算法。假设信号S(N)为非带限信号，理想的接收信号x(N)的功率谱如图2所示，虚线以下表示理想白噪声的功率谱，虚线以上表示信号的功率谱。

图2　非带限信号功率谱图

同样，对于接收信号先做功率谱估计，得到功率谱 Px(f)，由功率谱估计信号主瓣的频带范围[fL,fH]。在确定信号主瓣频带范围时，方法是通过对功率谱做差分得功率谱差分图，如图3所示。搜索功率谱差分图的最大值，向负方向遍历，求得第一零点的横坐标作为 fL；搜索功率谱差分图的最小值，向正方向遍历，求得第一零点的横坐标作为 fH；这种方法求出的是功率谱图的第一凹点，也就是无噪声情况下的第一过零点。

图3　非带限信号功率谱差分图

在此基础上，计算出信号主瓣频带范围内信号与噪声的功率之和：

(5)

用接收信号的总功率减去信号主瓣频带范围内信号与噪声的功率之和，得到主瓣频带范围外信号与噪声的功率之和：

(6)

于是，可列出如下方程组：

(7)

其中，PS表示信号功率；PN表示噪声功率；λ为信号主瓣频带范围与总的观测带宽之比，也就是主瓣频带范围内噪声功率与噪声总功率的比值；η为无噪声条件下信号的主瓣功率与信号总功率之比值，该比值只与信号的码元波形有关，可根据不同码元的功率谱计算。如，码元波形为矩形脉冲的信号主瓣功率与信号总功率之比约为0.902 8。而在通信系统中，信号的码元波形一般为已知条件。

解方程组，可得信噪比估计值：

(8)

新算法的本质是利用信号主瓣范围内与主瓣范围外的功率之比和噪声主瓣范围内与主瓣范围外功率之比来求得信号功率和噪声功率。新算法通过方程组求解信号功率和噪声功率，避免了因信号频带范围估计不准确而带来误差的问题，在功率谱估计理想的情况下，可以准确求出信号和噪声功率，不存在信号功率和噪声功率划分不清的问题，因而是一种无偏估计。即便噪声不理想导致估计频带范围存在一定的偏差，由于是在第一过零点附近，带内信号功率和带外信号功率的比值也不会偏离真实值太多，而噪声功率的比值并不会因频带范围估计不准受到影响，因此新算法对频带范围的估计误差有一定的容忍性。

新算法也可用于处理带限信号。用新算法处理带限信号时，η取1即可，这种情况下，新算法与传统算法是等效的。因此，传统算法可以看作是新算法的一种特殊情况。

算法步骤归纳如下：

3仿真分析

本节主要针对BPSK和QPSK等常用非带限卫星信号进行仿真验证，分析算法随信噪比变化的趋势以及适用的信噪比范围。仿真中主要用估计均值和均方根误差评价算法的估计性能。信噪比估计均值由下式计算得到：

(9)

(10)

在对新算法仿真的同时，仿真了传统的基于谱分析的信噪比估计算法(取主瓣作为频带范围)的性能作为对比。仿真条件：1.4 Mbps的码元速率，码元波形为矩形脉冲，载波为7 MHz，采样速率56 MHz，数据长度为4 096个采样点。进行500次蒙特卡洛仿真。

图4和图5为信噪比估计的均值图。从图中可以看出，正如前面所分析的那样，传统的基于谱分析的估计算法在信噪比较高时算法性能严重下降；而新的谱分析估计算法在-15～25 dB求得的均值都优于传统算法，一直在真值附近摆动，且在-12～13 dB估计值的均值偏离真值不超过0.5 dB。

图4　BPSK信号信噪比估计均值

图5　QPSK信号信噪比估计均值

图6和图 7为信噪比估计均方根误差曲线图。从中可以看出，当信噪比低于-10 dB时，传统算法和新算法的均方根误差都急速下降，这是因为当信噪比过低时，信号频带边界的判断会因噪声影响而呈现出随机性，导致均方根误差过大。当信噪比大于0 dB时，传统算法的均方根误差开始增大，而新算法由于更好的分辨了噪声能量和信号能量，在信噪比大于10 dB时，均方根误差才开始呈现明显增大。新的基于谱分析的信噪比估计算法在-10～10 dB均方根误差都基本小于0.5 dB。

综上，可以看出，新的基于谱分析的信噪比估计算法在估计均值和均方根误差性能上都较传统算法有较大的提升。无论在信噪比较低还是较高的情况下，算法的估计精度都得到了提高，在-10～10 dB能稳定精确地估计信号的信噪比，估计精度可达0.5 dB。算法对于BPSK和QPSK两种信号的估计性能基本一致。

图6　BPSK信号信噪比估计均方根误差曲线

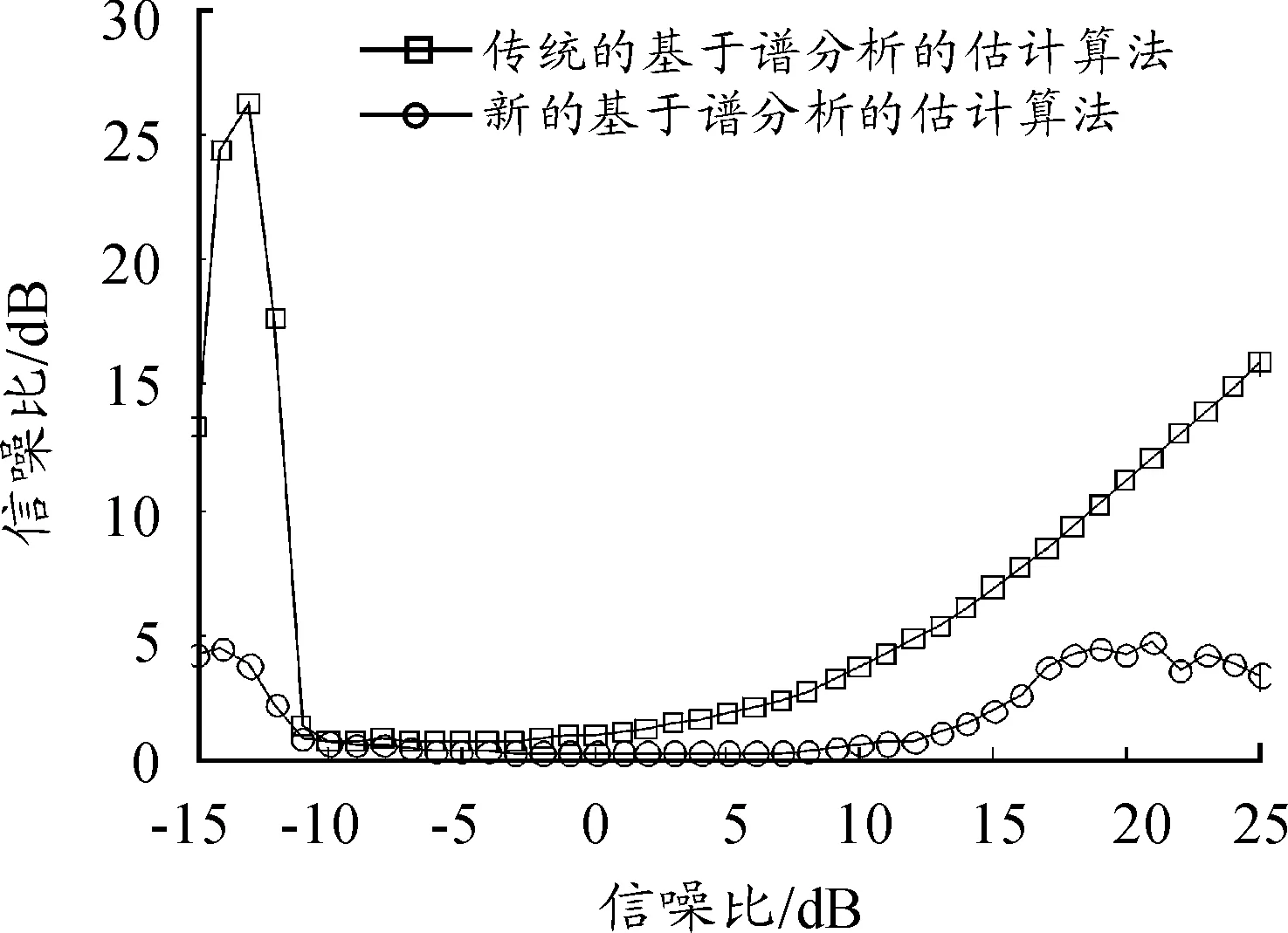
图7　QPSK信号信噪比估计均方根误差曲线

4小结

论文介绍了基于谱分析的信噪比估计算法的原理，分析了算法存在的缺陷及其对非带限信号的不适用性，通过分析产生导致这种现象的原因，提出了一种新算法。新算法通过细致区分功率谱估计图中的噪声功率和信号功率，改善了基于谱分析的信噪比估计算法的性能。且算法适用于各种不同的调制方式，计算量小，满足了对非带限卫星信号信噪比估计的需求。仿真结果验证了新算法的正确性。

参考文献：

[1]樊昌信，曹丽娜.通信原理[M].国防工业出版社,2010:212-213.

[2]彭耿，黄知涛，陆凤波，等.中频通信信号信噪比的快速盲估计[J].电子与信息学报，2010(1):102-106.

[3]张金成，彭华，赵国庆.信噪比估计算法研究[J].信息工程大学学报，2011(5):535-543.

[4]KERR R B.On Signal and Noise Level Estimation in a Coherent PCM Channel[J].IEEE Transactions on Aerospace and Electronic Systems.1966,AES-2(4):450-454.

[5]孟庆萍，周新力，田伟.基于先验信息辅助的8PSK信号信噪比估计[J].北京邮电大学学报，2012(4):94-98.

[6]SIMON M K,MILEANT A.SNR estimation for the baseband assembly[R].The Telecommunications and Data Acquisition Progress Report 42-85,January-March 1986.1986:118-126.

[7]SIMON M,DOLINAR S.Improving signal-to-noise ratio estimation for autonomous receivers[J].The Interplanetary Network Progress Report，2004,42:159.

[8]BENEDICT T,SOONG T.The joint estimation of signal and noise from the sum envelope[J].IEEE Transactions on Information Theory，1967,13(3):447-454.

[9]MATZNER R.An SNR estimation algorithm for complex baseband signals using higher order statistics[J].Facta Universitatis (Nis)，1993,6(1):41-52.

[10]ANDERSIN M,MANDAYAM N B,YATES R D.Subspace based estimation of the signal to interference ratio for TDMA cellular systems[J].Wireless Networks，1998,4(3):241-247.

[11]詹亚锋，曹志刚，马正新.无线数字通信的盲信噪比估计[J].清华大学学报(自然科学版)，2003,43(7):957-960.

[12]陈璐，毕大平，徐梁昊.时域重叠多输入/输出雷达信号分离算法[J].探测与控制学报，2015(5)：51-56.

[13]胡冰舟，张蓉，雷维嘉，等.一种基于平均周期图的频域信噪比估计算法[J].电讯技术，2014(10):1385-1390.

(责任编辑杨继森)

本文引用格式：易辉，侯孝民，马宏，等.一种基于谱分析的非带限卫星信号信噪比估计算法[J].兵器装备工程学报，2016(5):104-107.

Citation format:YI Hui,HOU Xiao-min,MA Hong,et al.An SNR Estimator Based on Spectrum Analysis for Non-Band-Limited Satellite Signals[J].Journal of Ordnance Equipment Engineering,2016(5):104-107.

An SNR Estimator Based on Spectrum Analysis for Non-Band-Limited Satellite Signals

YI Hui,HOU Xiao-min,MA Hong,WU Tao

(Equipment Academy,Beijing 101416,China)

Abstract:In order to estimate the SNR (Signal to Noise Ratio)of non-band-limited satellite signals in high precision,a new SNR estimator based on spectrum analysis was proposed after an investigation of the traditional SNR estimator based on spectrum analysis.The new estimator utilized the ratio of signal power in main lobe to total signal power and the ratio of noise power in main lobe to total noise power to calculate signal power and noise power,and then got the SNR.Simulations for BPSK (Binary Phase Shift Keying)and QPSK(Quadrature Phase Shift Keying)signals indicate that the new estimator is stable and can improve the estimation precision effectively.The bias and root mean square error of the new estimator are almost less than 0.5 dB when the true SNR range is from -10 dB to 10 dB.The new estimator can be used to different modulations.It has low complexity and can satisfy the SNR estimation demand of non-band-limited satellite signals.

Key words:SNR estimation; spectrum analysis; non-band-limited; satellite signal

doi:【信息科学与控制工程】10.11809/scbgxb2016.05.025

收稿日期：2015-10-25；修回日期：2015-11-29

作者简介：易辉(1991—)，男，硕士研究生，主要从事测控与通信技术研究。

中图分类号：TN571

文献标识码：A

文章编号：2096-2304(2016)05-0104-05