高速永磁同步电机电枢电流谐波分析

于吉坤，　李立毅，　杜鹏程，　张江鹏

(哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001)



高速永磁同步电机电枢电流谐波分析

于吉坤，李立毅，杜鹏程，张江鹏

(哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001)

摘要:在高速永磁同步电机谐波分析中，主要有解析和仿真两种方法。解析法则适用于连续系统，而仿真法适用于离散系统的，但两种方法之间关联性问题研究相对较少，针对此问题，提出一种基于空间矢量脉宽调制(SVPWM)技术电枢电流谐波解析法和仿真法内在关联的分析方法。根据连续函数和离散函数的傅里叶级数公式，分析了这两种方法在谐波计算中偏差的分布规律。分析结果表明，采样频率和负载是离散电枢谐波计算的主要影响因素，随着采样频率的升高电枢电流谐波呈现振荡阻尼衰减的特性，并收敛于连续系统的解析值，而负载则能降低振荡幅值和提高收敛速度。构建了基于DSP的永磁同步电机系统实验平台，实验结果验证了该分析方法的有效性。

关键词:高速永磁同步电机；空间矢量脉宽调制；电枢电流；谐波分析；离散傅里叶变换

0引言

由于采用磁能积高的稀土永磁材料作励磁，与传统的电机相比，高速永磁电机具有更高的功率密度，更高的可靠性，以及更小的尺寸比等优势，近年来引起业界极大兴趣和广泛研究[1-2]。这种类型的电机有许多工业应用，如压缩机，真空泵，涡轮发电机，飞轮储能系统，钻孔工具，摩擦焊接设备等。在这些高速工业单元中，省去了变速箱中间环节，应用直接与电机的转轴连接，不仅缩小了设备体积，而且提高了设备的传动效率和系统可靠性[3-4]。

高速永磁电机磁路中串联的稀土钴和钕铁硼永磁材料导磁性能很弱，相对磁导率约为1，另外，高速永磁电机电路通入电流频率很高，减少了电枢匝数，降低高速永磁电机的电感值。在高速电机驱动控制系统中，主电路广泛使用电压源型PWM逆变电路，电枢电压在正负母线频繁切换，与反电势的压差降落在小电感绕组电路中，会产生丰富的谐波电枢电流，引入额外的电磁损耗和机械振动等问题，而这些问题又多以电流谐波作为理论分析出发点[5]。目前谐波分析主要有仿真法[6-10]和解析法[11-12]两种方法，仿真法适用性很强，谐波含量直观清晰，但与电机系统参数之间的关系不够明确，解析法以数学表达式的形式建立起与电机系统参数之间的联系，能够深刻的揭示谐波随参数变化规律，但推导复杂，仅少数PWM调制方式的电枢电流谐波能得到完美的解析解，在简化解析计算中也多以电压谐波分析为主[13-14]。目前有关电机电压和电流谐波分析中，多以离散仿真方法验证解析方法，而对于两种方法之间的关系研究的很少，尚未见诸他刊。

本文以SVPWM调制技术的高速永磁同步电机系统为例，研究高速电枢电流在实际连续时间系统与在仿真和实验测试离散时间系统的谐波计算方法的问题，揭示两种系统中谐波分析结果的内在联系和区别。连续系统中电枢电流谐波解析算法可以作为其他谐波损耗和振动的理论基础，又能为离散系统离散的电枢电流谐波准确计算提供指导。

1SVPWM工作原理

在变压变频调速系统中，永磁同步电机通常由电压型三相桥式PWM逆变电路供电，如图1所示，图中，电容C假想中性点O接地，三相桥臂组成半桥拓扑形式，桥臂与电机相绕组一一对应连接，每相电阻绕组等效为电阻R、电感L和反电势e串联等效电路图，三相绕组星接，其中性点用N表示。

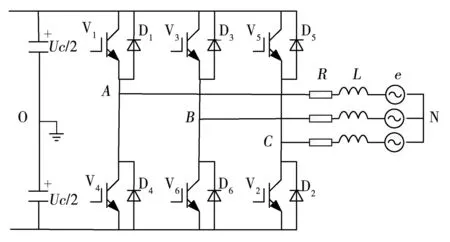
图1　三相桥式PWM逆变电路Fig.1　Three phase bridge PWM inverter circuit

每相桥臂由互补导通的功率开关器件组成，当上桥臂器件导通时用数字1表示，而下桥臂器件导通时用数字0表示，三相桥臂开关器件共有8种工作状态，分别是100、110、010、011、001、101、000、111，并分别用8个矢量U1～U8表示，它们共同组成了图2所示电压空间矢量六边形，公式形式如式(1)所示。

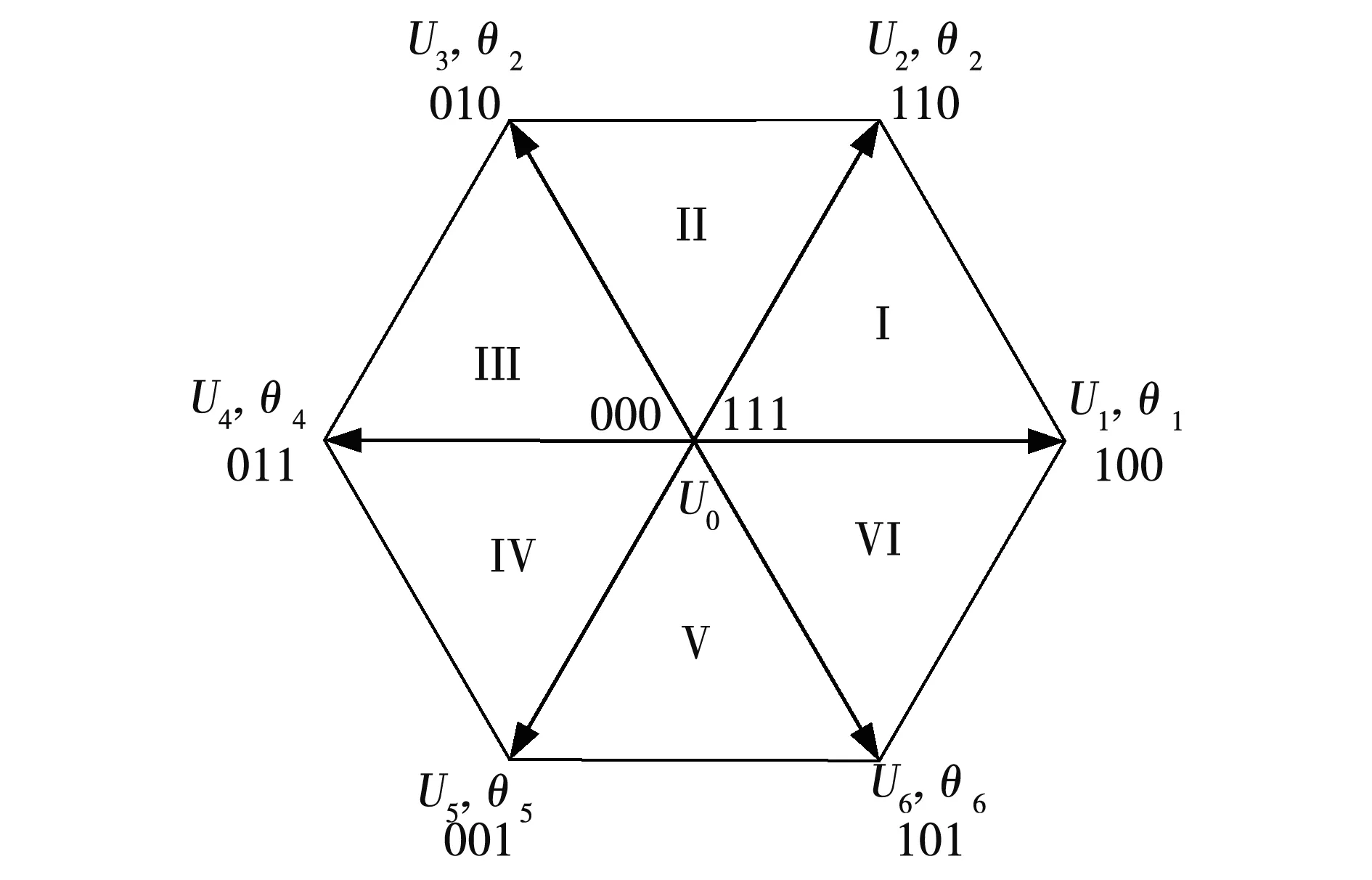
图2　电压空间矢量六边形Fig.2　Hexagonal voltage space vector

(1)

式中：s(s=1,2,3,……)为扇区号，Us、θs为合成电压矢量的幅值、相角。

根据矢量合成法则，可根据前面所述6个非零电压空间矢量获得所需幅值和相位的电压空间矢量，如图3所示。通常根据目标矢量所在的扇区，表示为相邻的矢量线性组合，见式(2)。将式(1)代入式(2)，就可以求解出相邻矢量作用时间，如式(3)所示，一般相邻矢量作用时间和小于扇区时间Tc，剩余时间T0就作为零矢量作用时间即式(4)。

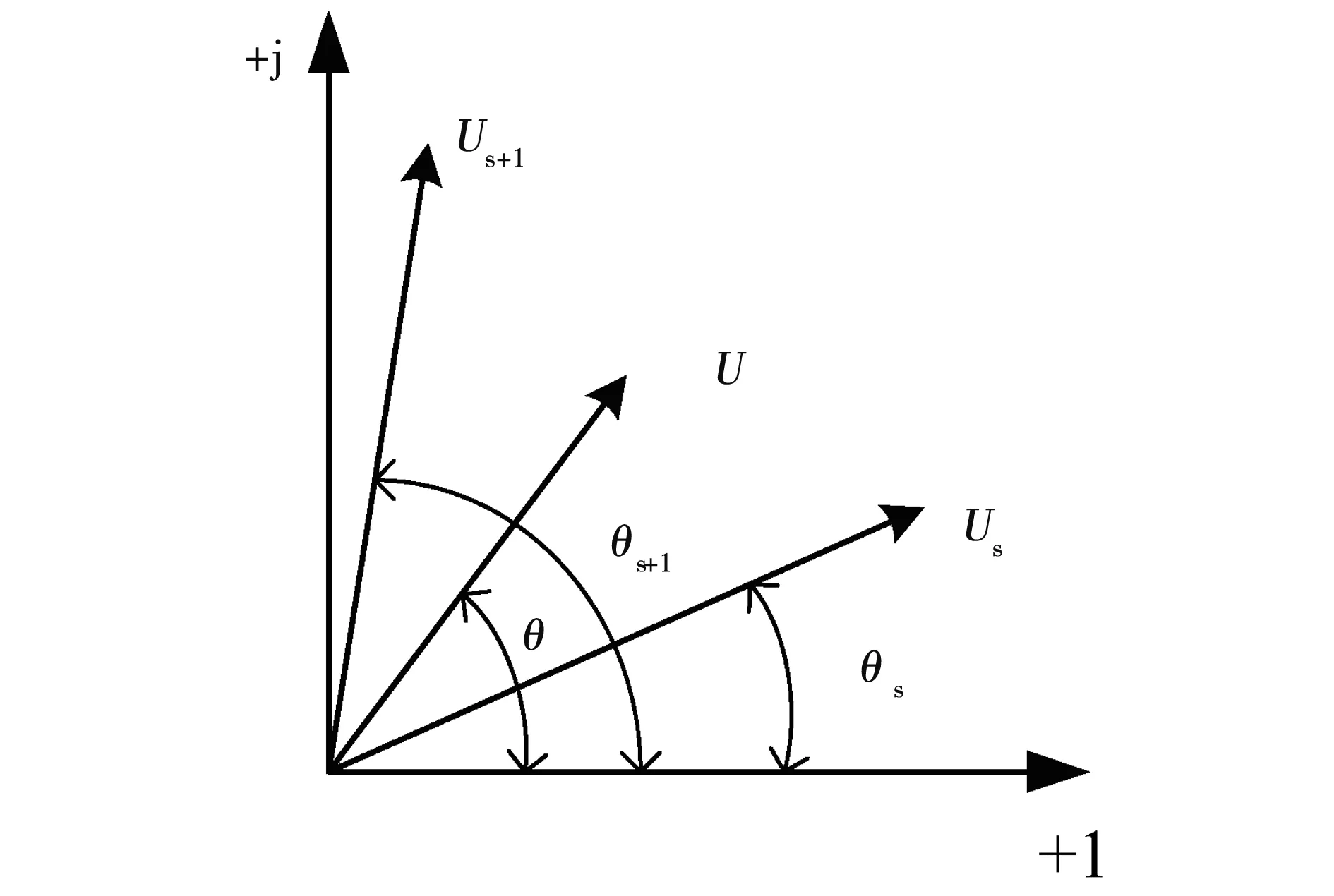
图3　空间电压矢量的线性组合Fig.3　The linear combination of space voltage vector

(2)

(3)

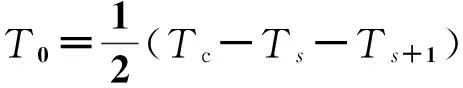
(4)

表1列出了任意目标矢量在相应扇区合成所需的非零相邻矢量及相应的作用时间，作用时间与目标矢量幅值和相位直接相关，其中M表示调制比，是目标矢量幅值U与电容电压UC之半的比值。

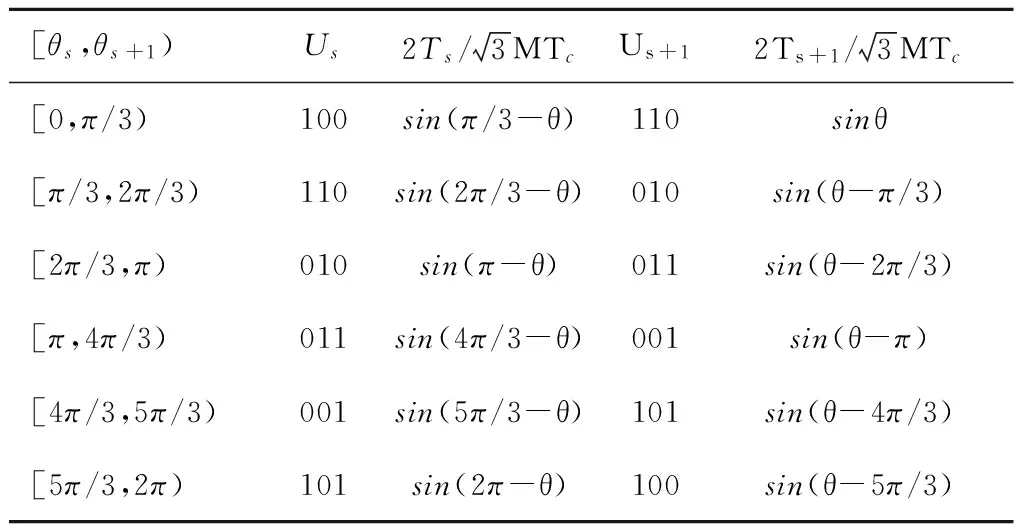
表1　目标矢量所需的非零相邻矢量及其作用时间

以A相桥臂为例，根据表1信息，就可以得出每个扇区内A相高电平作用时间T和占空比D，见表2。为降低器件通断损耗，常插入零矢量，以确保每次工作状态切换时只改变一个桥臂器件通断状态，从表2中可以看出每个扇区内切换时都有零矢量作用时间，或是000，或是111，它们各占零矢量时间T0的二分之一。

表2　A相高电平时间及其占空比

2谐波分析

电机稳态工作时，三相绕组电压空间合成矢量以同步角频率ω1匀速旋转且重复循环，因此，施加在绕组上电压、电流和磁链是连续时间周期函数曲线，统一用f(t)表示，周期函数就可以表示为三角函数的傅里叶级数的形式，其余弦系数an和正弦系数bn表达式为：

(5)

式中：T1为同步输出周期，满足T1=2π/ω1。

然而，在实际永磁同步电机控制系统中，六拍阶梯波的逆变电路是不能使电机平滑运转的，需对扇区细致划分，划分以开关周期为单位，每个开关周期内都有一个PWM脉冲，如图4所示，给出第k个开关周期内PWM脉冲的通断时序，通断时间分别用t2k和t2k-1表示，据此可得到每个开关周期内PWM脉冲通断时刻的表达式(6)。

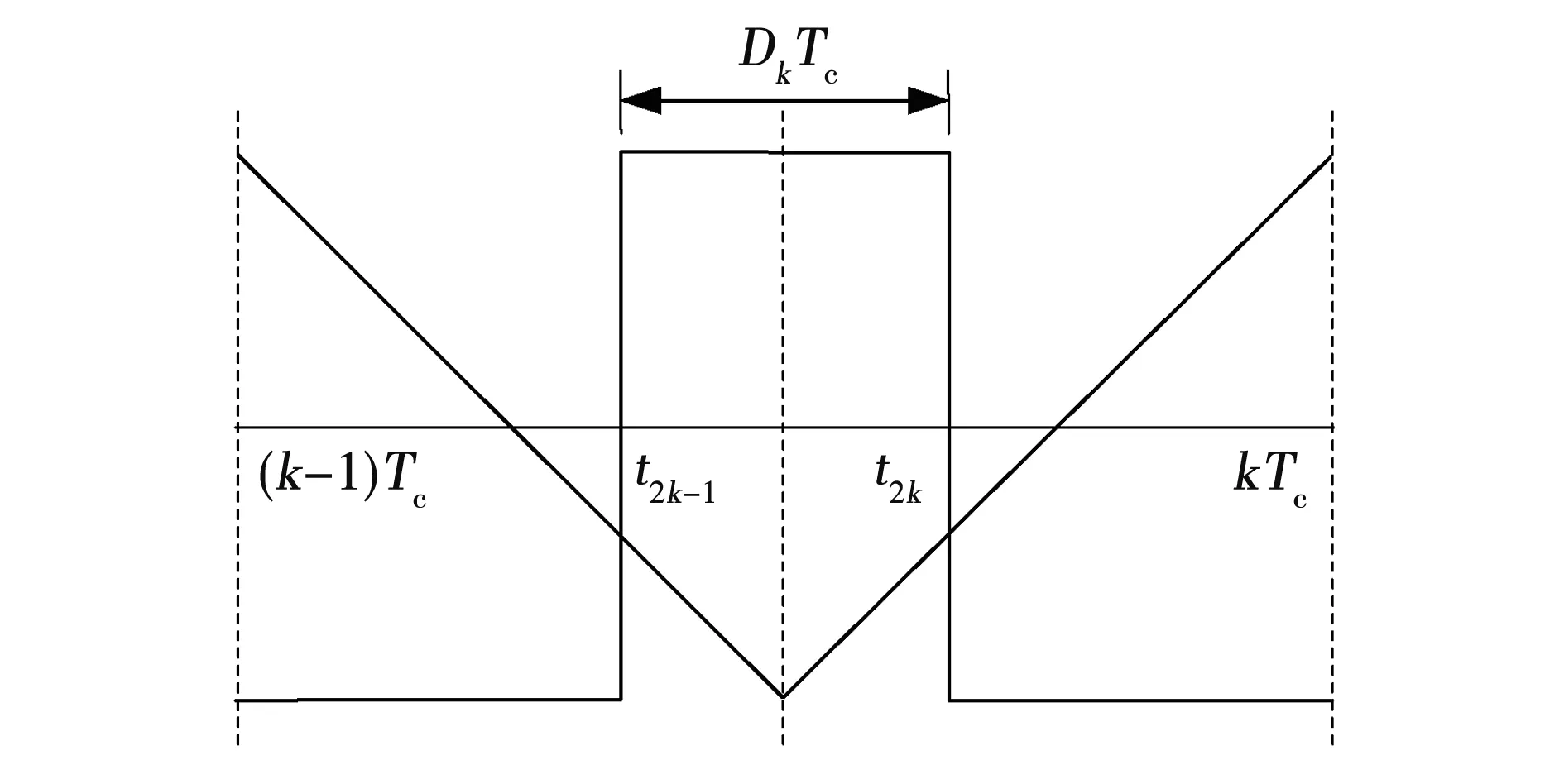
图4　第k个开关周期内PWM脉冲通断时序Fig.4　　　　On-off time sequence of PWM pulse in　　　 the kth switching period

(6)

经推导可得到周期变化相电压PWM傅里叶级数系数表达式

(7)

式中：anu为相电压余弦系数，bnu为相电压正弦系数，Nc为载波比。特别地，当n为3的整数倍时，anu和bnu均为零。进一步地，将式(7)代入永磁同步电机电压平衡方程式就可以推导出，电枢绕组电流谐波系数表达式

(8)

式中：ani为相电压余弦系数，bni为相电压正弦系数，an(u-e)为相电压与相反电势之差的余弦系数，bn(u-e)为相电压与相反电势之差正弦系数。

表3列出了本文所用系统的电机模型参数和控制参数，采用转子磁场定向矢量控制方式，根据电枢电流谐波解析表达式，分别绘制了电机空载和负载时前60次的频谱图。从频谱图中可以看出，主要谐波集中在载波比倍次附近，如Nc±2、2Nc±1、3Nc±2，除此之外，还在幅值较高的低次谐波如2次和4次。表4列出空载和负载时基波、低次谐波(2次和4次)、载波比倍次谐波(13次、29次和43次)具体解析结果，从表中数据对比来看，在本系统参数情况下，负载对电枢电流谐波幅值影响较小。

表3　仿真系统及实验系统所使用电机及控制的参数

图5　载波比Nc=15时电流谐波解析结果Fig.5　　　　Analytical results of the current harmonics　　　 with carrier ratio Nc=15

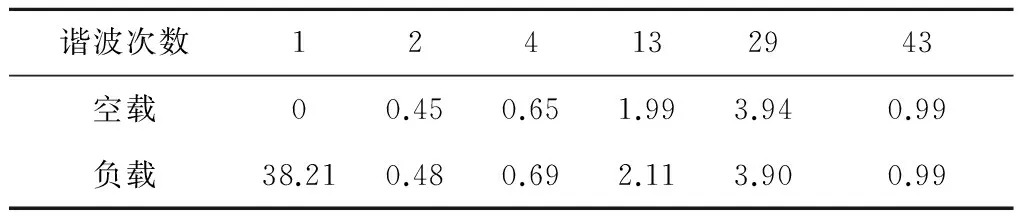
谐波次数124132943空载00.450.651.993.940.99负载38.210.480.692.113.900.99

3仿真结果

在Matlab/SIMULINK环境中对所提出的电枢电流谐波计算方法进行了仿真分析，仿真系统所用的电机模型参数和控制参数见表2。以时间间隔为Tsam=1 μs即采样频率fsam=1 MHz为例，图6绘制了空载和负载情况下电压和电流的仿真波形。

由于仿真得到的电压和电流波形不再是时间连续的周期函数波形，就不能按照式(5)傅里叶级数展开，此时需要根据离散傅里叶变换(DFT)处理，式(9)给出了DFT正向和逆向变换公式，通过复数指数形式，将实数域离散点x变换到复数域离散点X。

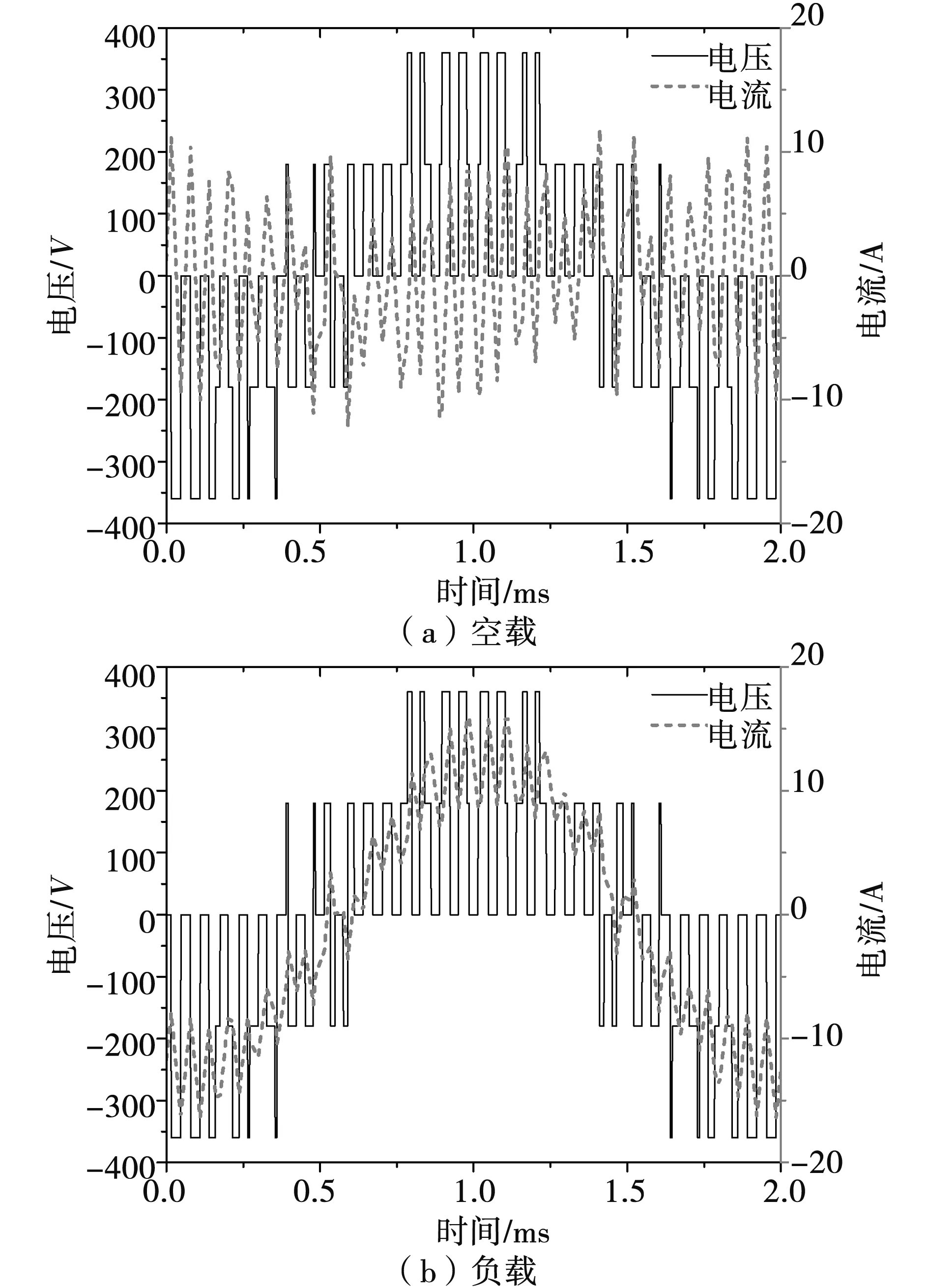
图6　PWM电压供电时电流波形仿真结果Fig.6　　　　Simulation results of the current waveform　　　 with PWM voltage excitation

(9)

离散周期函数尽管不能表示成无穷级数的形式，仍然可以按照其形式对式(9)逆向DFT公式整理，得

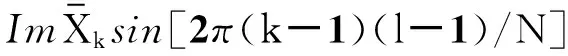
(10)

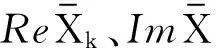
(11)

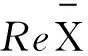
(12)

在仿真系统中样本数N取一个同步输出周期内采样点的个数Nsam，即Nsam=T1/Tsam，图6所用的为Nsam=1 876，这样就可以计算出离散周期数据的谐波幅值，改变Nsam就可以得出不同采样频率时各次谐波幅值。为此，着重对幅值较高的低次谐波(1、2、4)和高次谐波(13、29、43)进行仿真计算，仿真结果见图7和图8。

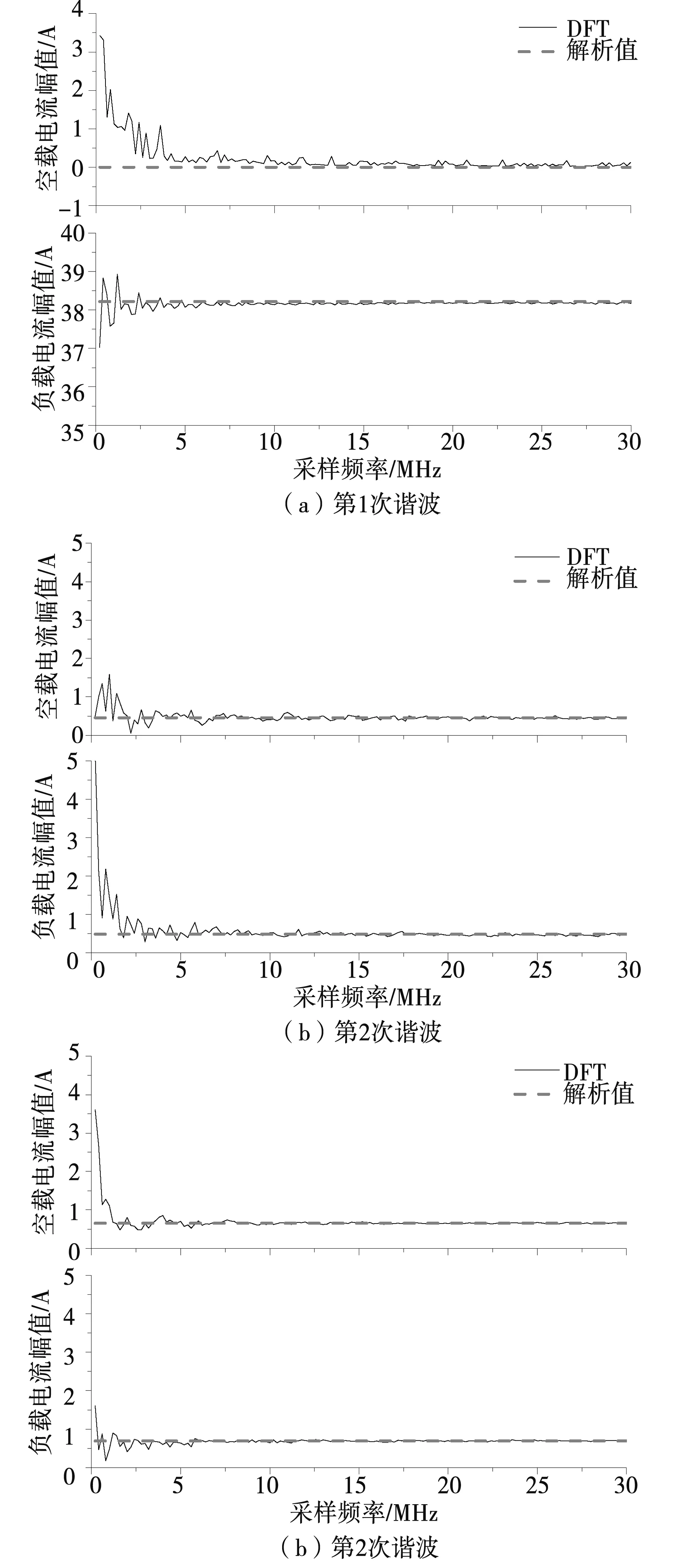
图7　低次谐波电流幅值仿真结果Fig.7　　　　Simulation results of the low order 　　　harmonics current amplitude

图8　高次谐波电流幅值仿真结果Fig.8　　　　Simulation results of the high order 　　　harmonics current amplitude

从图7和图8可以看出，各次谐波幅值随采样率振荡变化，采样率越低，仿真DFT值越振荡幅度越大，采样率越高，仿真DFT值越趋近收敛于解析值，采样率对低次谐波比对高次谐波影响更为剧烈。采样率越高离散时间系统越接近连续时间系统，另外，随着负载的加入，各次谐波幅值振荡幅值减小，收敛速度加快。从收敛角度讲，仿真计算结果也验证了所提出的电枢电流谐波计算方法的正确性。

4实验结果

为了验证算法以及仿真结果的正确性，实验研究在实验室永磁同步伺服电机系统上进行，图9为实验系统平台的实物图。控制器逆变电路如图1所示，功率开关器件为IGBT，核心控制单元为TMS320F2808，其他实验系统参数见表2，采用转子磁场定向的矢量控制控制策略和SVPWM调制方式。用泰克Tektronix TPS2014和横河Yokogawa DLM2054示波器观测记录相电流，用涡电流测功机Magtrol 2WB115施加负载。

图9　实验系统实物图Fig.9　Photograph of experimental System

针对采样率对离散时间数据DFT谐波幅值的影响，使用具有不同采样能力的示波器对相电流进行记录，用泰克示波器记录1 MHz低采样频率时的相电流波形数据，用横河示波器记录25 MHz高采样频率时的相电流波形数据，他们记录的时间间隔分别是1 μs和40 ns，在一个输出周期1.875 ms中，两种示波器能记录到的数据点数分别为1 876和46 876。将记录的数据分为低采样频率和高采样数据两组，分别与仿真结果的对应采样频率进行对比。

图10、图11是1 MHz采样频率时空载和负载实测波形。图12、图13是25 MHz采样频率时空载和负载实测波形为便于与仿真结果对比，对实测离散数据也进行了DFT处理，并绘制了电枢电流谐波频谱图。实验波形与仿真波形较为吻合，谐波频谱也较为一致。

图10　采样频率fsam=1 MHz时空载实验结果Fig.10　　　　Experimental results of no load with 　　　sampling frequency fsam=1 MHz

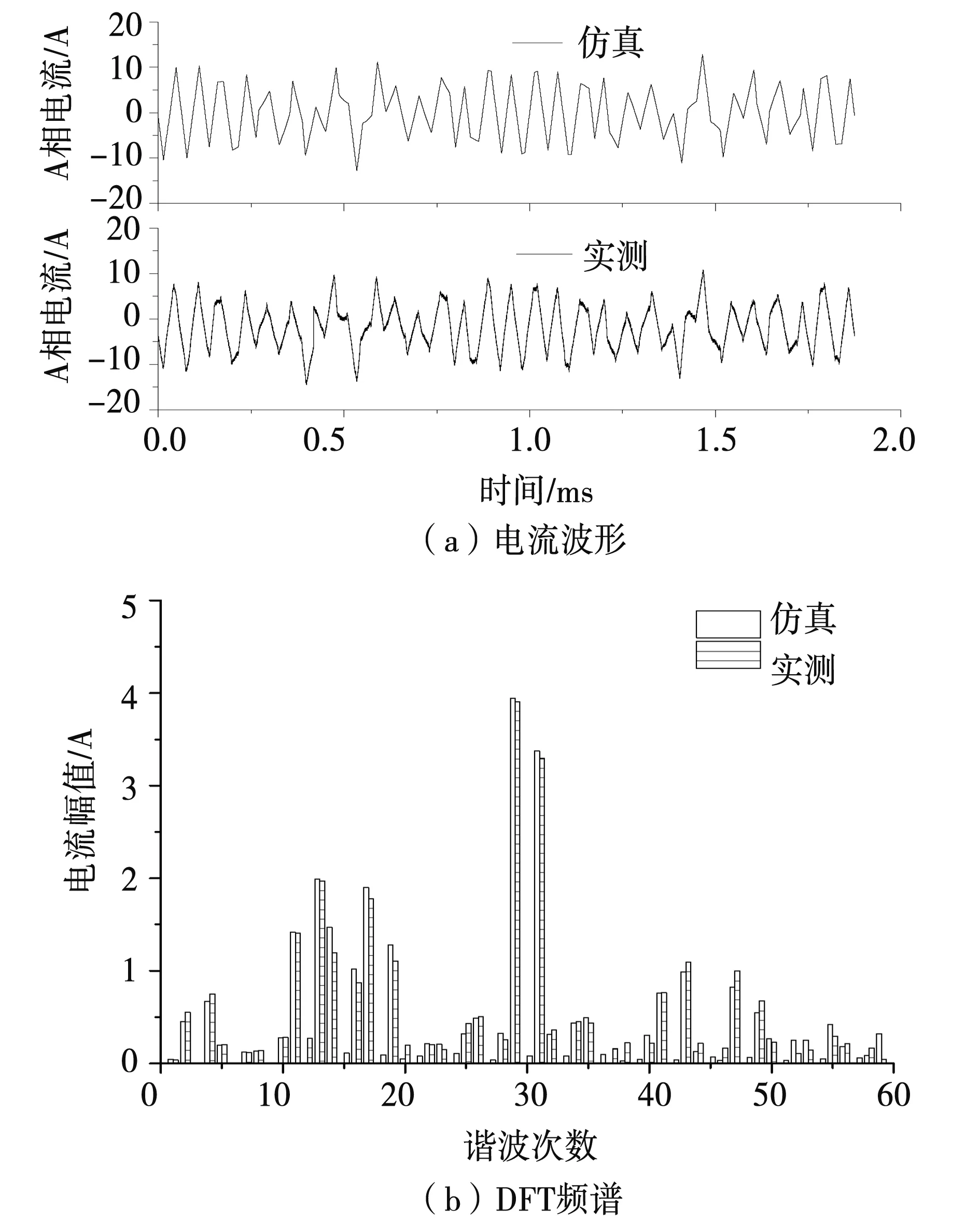
图12　采样频率fsam=25 MHz时空载实验结果Fig.12　　　　Experimental results of no load with 　　　sampling frequency fsam=25 MHz

图13　采样频率fsam=25 MHz时负载实验结果Fig.13　　　　Experimental results of full load with 　　　sampling frequency fsam=25 MHz

表5、表6分别是1 MHz和25 MHz采样频率时，较高幅值的谐波，结合表3，就可以发现与仿真结果一致的规律，低次谐波与解析结果偏差大，高次谐波与解析结果偏差小，增大采样频率，可提高离散数据DFT谐波幅值的计算精度，另外，负载时的仿真和实测值更接近于理论解析值，证实了前面的连续系统和离散系统在电枢电流谐波计算中所作的理论分析。

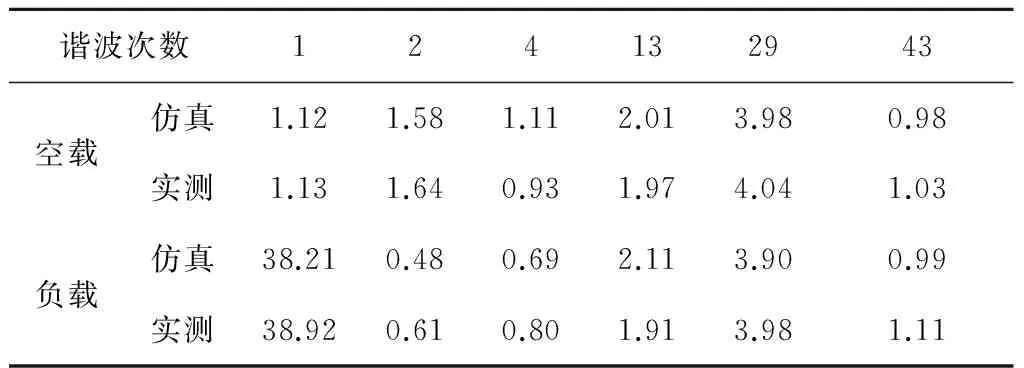
表5　采样频率fsam=1 MHz时电流计算值和实验值比较

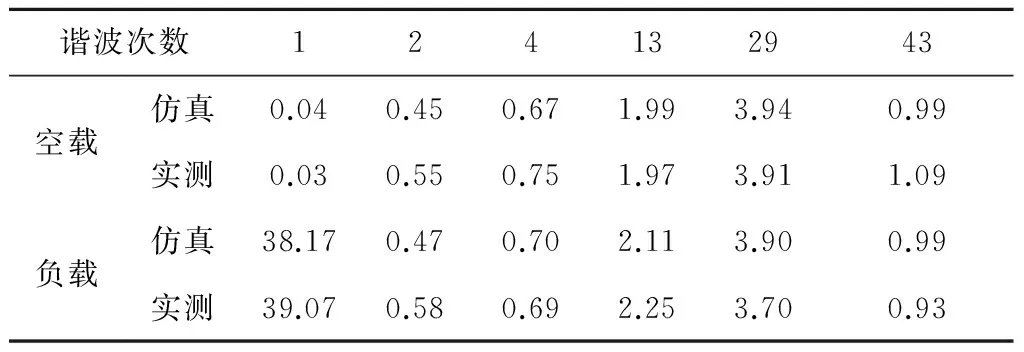
表6　　　　采样频率fsam=25 MHz时电流计算值和实验值比较

5结论

本文对高速永磁同步电流电枢电流谐波进行解析计算，通过周期连续时间SVPWM电压脉冲序列的傅里叶无穷级数，结合永磁同步电机电压平衡方程，推导出电枢电流谐波计算公式。考虑到数据采集离散性特点，仿真和实验结果需经离散傅里叶变换(DFT)得到谐波频谱。仿真结果表明采样率和负载是离散数据谐波的主要影响因素，随着采样频率的升高电枢电流谐波呈现振荡阻尼衰减的特性，并收敛于所提方法的解析值，而负载则能降低振荡幅值和提高收敛速度，通过仿真验证了所提方法的正确性，在基于DSP的永磁同步电机系统实验平台上得出的实验结果与仿真结果基本吻合，验证了所提方法及其与离散系统谐波计算之间规律关系的有效性。

参 考 文 献:

[1]王继强, 王凤翔, 鲍文博,等. 高速永磁电机转子设计与强度分析[J]. 中国电机工程学报, 2005, 25(15): 140-145.

WANG Jiqiang, WANG Fengxiang, BAO Wenbo, et al. Rotor design and strength analysis of high speed permanent magnet machine[J]. Proceedings of the CSEE, 2005, 25(15): 140-145.

[2]吴震宇, 曲荣海, 李健,等. 表贴式高速永磁电机多场耦合转子设计[J]. 电机与控制学报, 2016, 20(2): 98-103.

WU Zhenyu, QU Ronghai,LI Jian,et al. Multi-field coupling rotor design for surface-mounted high-speed permanent magnet machine[J]. Electric Machines and Control, 2016, 20(2): 98-103.

[3]KOLONDZOVSKI Z. Power limits of high-speed permanent-magnet electrical machines for compressor applications. IEEE Transactions on Energy Conversion, 2011. 26(1): 73-82.

[4]于吉坤. 宽弱磁调速范围永磁同步主轴电机的研究[D]. 哈尔滨：哈尔滨工业大学，2011.

[5]李立毅, 于吉坤, 曹继伟, 等. 基于PWM逆变电路供电的永磁同步电机电压和电流的谐波通用型新算法[J]. 中国电机工程学报, 2015, 35(23): 6203-6213.

LI Liyi, YU Jikun, CAO Jiwei, et al. A Universal and New Harmonic Algorithm of Voltage and Current of Permanent Magnet Synchronous Motors Supplied By PWM Inverter[J]. Proceedings of the CSEE, 2015, 35(23): 6203-6213.

[6]周明磊, 游小杰, 王琛琛, 等. 电流谐波最小 PWM 开关角的计算及谐波特性分析[J]. 中国电机工程学报, 2014, 34(15): 2362-2370.

ZHOU Minglei, YOU Xiaojie, WANG Chenchen, et al. Switching angle calculation and harmonic analysis of current harmonic minimum PWM[J]. Proceedings of the CSEE, 2014, 34(15):2362-2370.

[7]HAVA A, CETIN N. A generalized scalar PWM approach with easy implementation features for three-phase three-wire voltage-source inverters[J]．IEEE Transactions on Power Electronics, 2011, 24(5): 1385-1395.

[8]KANCHAN R S, BAIJU M R, MOHAPATRA K K, et al. Space vector PWM signal generation for multilevel inverters using only the sampled amplitudes of reference phase voltages[J]. IEE Proceedings of Electric Power Applications, 2005, 152(2): 297-309.

[9]BIERHOFF M, FUCHS F. DC-link harmonics of three-phase voltage-source converters influenced by the pulse width modulation strategy-an analysis[J]．IEEE Transactions on Industrial Electronics, 2008, 55(5): 2085-2092.

[10]CARRARA G, GARDELLA S, MARCHESONI M. A new multilevel PWM method: a theoretical analysis[J]. IEEE Trans on Power Electronics, 1992, 7(3):497-505.

[11]MCGRATH B P, HOLMES D G. An analytical technique for the determination of spectral components of multilevel carrier-based PWM methods[J]. IEEE Transactions on Industrial Electronics. 2002, 49(4): 847-857.

[12]陈瑶, 童亦斌, 金新民. 基于PWM整流器的SVPWM谐波分析新算法[J]. 中国电机工程学报, 2007, 27(13): 76-80.

CHEN Yao, TONG Yibin, JIN Xinmin. A novel algorithm of SVPWM harmonic analysis based on PWM rectifier[J]. Proceedings of the CSEE, 2007, 27(13): 76-80.

[13]吴晓新, 柳巍, 阮毅, 等．一种SVPWM过调制算法及其在两电平逆变器中的应用[J].电机与控制学报,2015,19(1):76-81.

WU Xiaoxin, LIU Wei, RUAN Yi, et al．SVPWM over-modulation algorithm and its applicationin two-level inverter[J]. Electric Machines and Control, 2015, 19(1): 76-81.

[14]朱建林, 张建华, 郭有贵，等. 过调制矩阵变换器的电压传输特性及谐波分析[J]. 中国电机工程学报, 2007,27(10): 110-113.

ZHU Jianlin, ZHANG Jianhua, GUO Yougui, et al. Voltage transfer characteristic and Harmonic analysis of matrix converter under over modulation[J]. Proceedings of the CSEE, 2007,27(10): 110-113.

(编辑：张楠)

Harmonic analysis of armature current for high speed permanent magnet synchronous motor

YU Ji-kun,LI Li-yi,DU Peng-cheng,ZHANG Jiang-peng

(School of Electrical Engineering and Automation, Harbin Institute of Technology, Harbin 150001, China)

Abstract:There are two methods in harmonic analysis of the high speed permanent magnet synchronous motor, and they are analytical method and simulation method. The analytical method is suitable for continuous systems, and the simulation method for discrete system.As the relevance of these two methods has been rarely studied, one correlation analysis method was proposed, which is based on the space vector pulse width modulation (SVPWM) technology. From Fourier series of the continuous function and the discrete function,the deviation distribution law between these two methods in the harmonic calculation was analyzed. The analysis results show that the main influence factors of discrete harmonic calculation of armature are sampling frequency and load condition.The armature current harmonics oscillate damping attenuation with increase in sampling frequency and converge to the analytical results of the continuous system. The oscillation amplitude is reduced and the convergence speed is improved by load. The permanent magnet synchronous motor system experiment platform based on DSP is constructed, and it is confirmed that the correlation analysis method is effective.

Keywords:high speed permanent magnet synchronous motor; space vector pulse width modulation (SVPWM); armature current; harmonic analysis; discrete fourier transform (DFT)

收稿日期:2014-11-06

基金项目：国家杰出青年科学基金(51225702)

作者简介：于吉坤(1987—)，男，博士研究生，研究方向为高速永磁电机的本体设计与特性分析；李立毅(1969—)，男，博士，教授，博士生导师，研究方向为特种电机及其控制；杜鹏程(1988—)，男，博士研究生，研究方向为高速永磁电机的驱动控制；张江鹏(1985—)，男，博士研究生，研究方向为高效率永磁电机的本体设计与特性分析。

通讯作者:李立毅

DOI:10.15938/j.emc.2016.05.005

中图分类号:TM 355

文献标志码:A

文章编号:1007-449X(2016)05-0028-09