A Riemann-Hilbert Approach to the Harry-Dym Equation on the Line∗

Yu XIAO Engui FAN

1 Introduction

The following nonlinear partial differential equation

is known as the Harry-Dym equation(see[1]).This equation was obtained by Harry Dym and Martin Kruskal as an evolution equation solvable by a spectral problem based on the string equation instead of the Schrödinger equation.The Harry-Dym equation plays an important role in the study of the Saffman-Taylor problem which describes the motion of a two-dimensional interface between a viscous and a nonviscousfluid(see[2]).The Harry-Dym equation shares many of the properties typical of the soliton equations.It is a completely integrable equation which can be solved by the inverse scattering transform(see[3]).It has a bi-Hamiltonian structure(see[4]),an in finite number of conservation laws and in finitely many symmetries(see[5]),and has reciprocal Backlund transformations to the KdV equation(see[6]).The Harry-Dym equation has been solved by different methods such as the inversing scattering method(see[3]),the B¨acklund transformation technique(see[7]),and the straightforward method(see[8]).Especially,Wadati obtained the one-cusp soliton solution(see[3])

by using inverse scattering transformation.

The main aim of this paper is to develop the inversing scattering method,based on a Riemann-Hilbert problem for solving nonlinear integrable systems,which has further developed and applied many equations with initial value problems on the line(see[9–11])and initial boundary value problems on the half line(see[12–17]).In this paper,we consider the initial value problem of the Harry-Dym equation

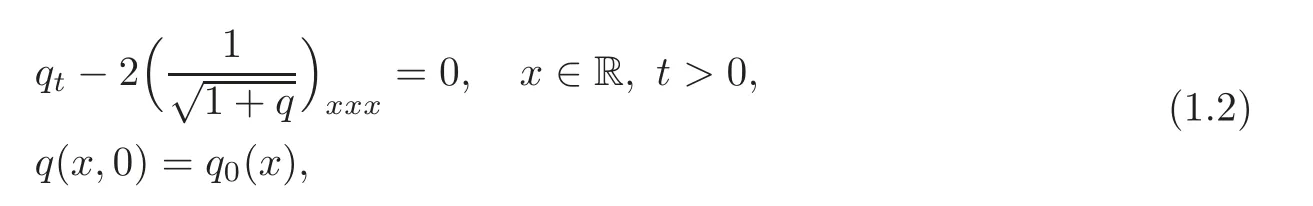
where the q0(x)is a smoothly real-valued function and decays as|x|→ ∞.The organization of the paper is as follows.In the following Section 2,we perform the spectral analysis of the associated Lax pair for the Harry-Dym equation.In Section 3,we formulate the main Riemann-Hilbert problem associated with the initial value problem(1.2).In Section 4,we obtain the one-cusp soliton solution in terms of the Riemann-Hilbert problem,which has a similar,but not the same,form constructed by the inverse scattering method(see[3]).

2 Spectral Analysis

2.1 A Lax pair

In general,the matrix Riemann-Hilbert problem is defined in the λ plane and has explicit(x,t)dependence,while for the Harry-Dym equation(1.2),we need to construct a new matrix Riemann-Hilbert problem with explicit(y,t)dependence,where y(x,t)is a function unknown from the initial value condition.For this purpose,we make a transformation

and(1.2)can be expressed by

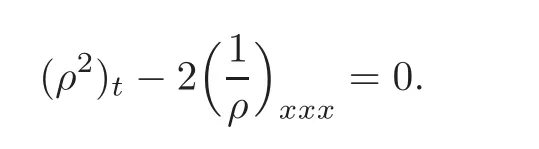
Then the initial value problem(1.2)is transformed into

It was shown that(1.2)admits the following Lax pair(see[3]):

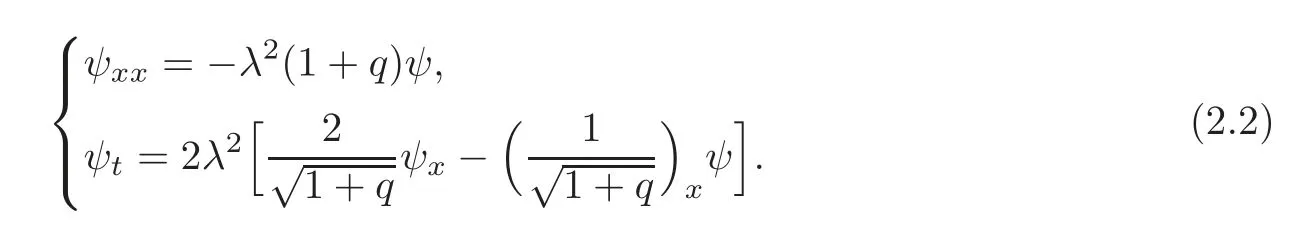
Making a transformation then the Lax pair(2.2)can be written in the matrix form

where

Further,by the gauge transformations

we have

where

It is clear that as|x|→ ∞,U(x,t)→ 0 and V(x,t,λ)→ 0.We define a real-valued function y(x,t)by

It is obvious that

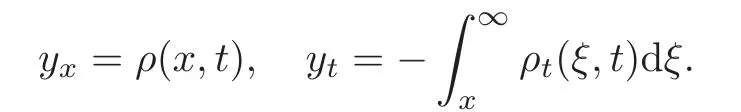
The conservation law

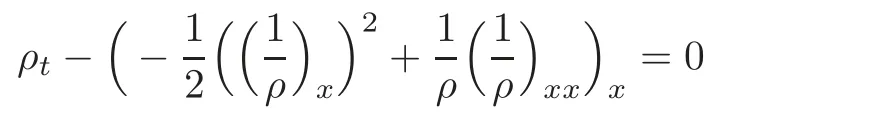
implies that

Extending the column vector φ to be a 2×2 matrix and letting

then μ solves

which can be written in the full derivative form

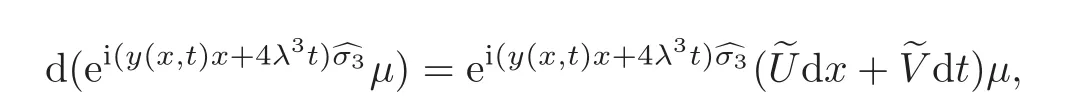
where

and[σ3,μ]= σ3μ − μσ3.As|x| → ∞,→ 0.The lax pair in(2.5)is very convenient for dedicated solutions via the integral Volterra equation,which is also what we study in the following paper.

Remark 2.1 By the representation of M,N and U,V in(2.3)and(2.4)respectively,wefind that ψx,ψtand φx,φthave no singularity in λ =0.Therefore,φ has no real singularity in λ=0.

2.2 Eigenfunctions

We define two eigenfunctions μ±of(2.5)as the solutions of the following two Volterra integral equations in the(x,t)plane:

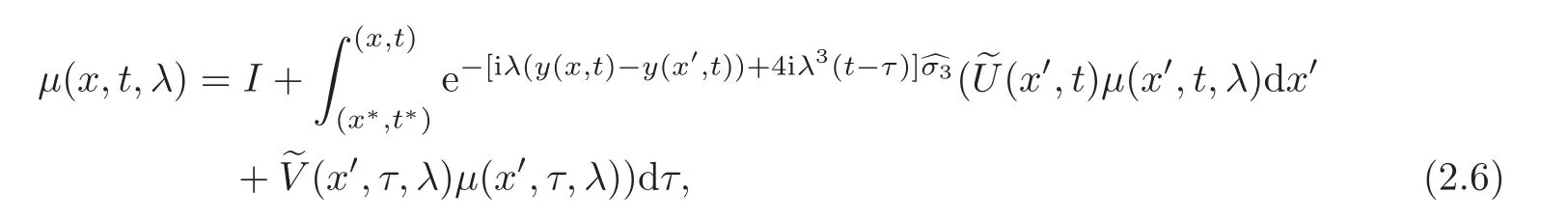
where I is a 2×2 identity matrix,andacts on a 2×2 matrix A bySince the integrated expression is independent of the path of integration,we choose the particular initial points of integration to be parallel to the x-axis and obtain that for μ+and μ−,

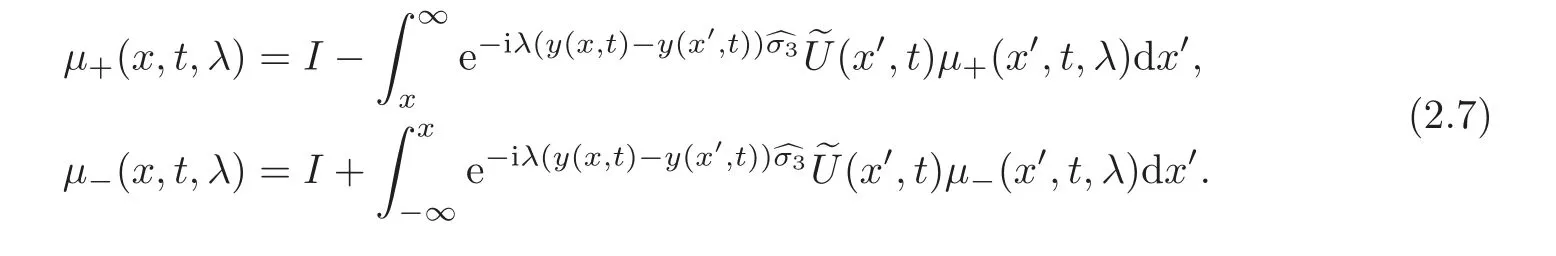
De fine the following sets:

Since for any fixed t,yx=ρ(x,t)>0,y(x,t)is an increasing function of x for fixed t.As x−x?<0,y(x,t)−y(x?,t)<0;as x−x?>0,y(x,t)−y(x?,t)>0.We can deduce that the second column vectors of μ+and μ−are bounded and analytic for λ ∈ C provided that λ belongs to D1and D2,respectively.We denote these vectors with superscripts(1),(2)to indicate the domains of their boundedness.Then

For any x and t,the following conditions are satisfied:

2.3 Spectral functions

For λ ∈ R,the eigenfunctions μ+,μ−being the solution of the system of differential equations(2.5)are related by a matrix independent of(x,t).We define the spectral function by

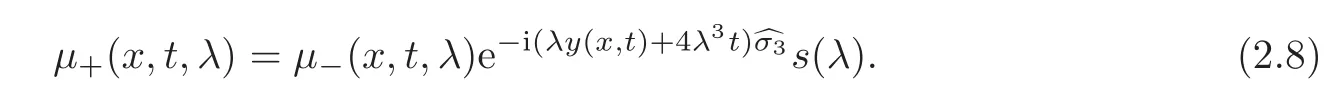
From(2.5),we get

Sincethe μ±(x,t,λ)have the relations:

The spectral function s(λ)can be written as

From the(2.9),det(s(λ))=1.Equations(2.8)–(2.9)imply that a(λ)and b(λ)have the following properties:

(1)a(λ)is analytic in D1and continuous for λ ∈

(2)b(λ)is continuous for λ ∈ R.

(3)

(4)a(λ)=1+O,λ→∞,λ∈D1.

(5)b(λ)=O??,λ→∞,λ∈R.

2.4 Residue conditions

We assume that a(λ)has N simple zerosin the upper half plane.These eigenvalues are purely imaginary.The second column of(2.8)is

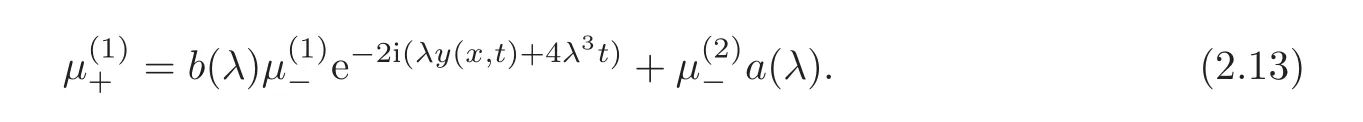
For(2.9)and(2.13),it yields

where we have used that both sides are well defined and analytic in D1to extend the above relation toHence,if a(λj)=0,the,are linearly dependent vectors for each x and t,i.e.,there exist constants bj?=0 such that

Recalling the symmetries in(2.10),wefind

Consequently,the residues

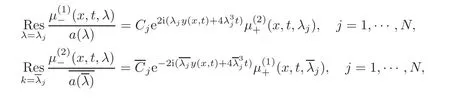
where

Remark 2.2 There is the relation of μ±that the s(λ)is the scattering matrix for the one-dimensional Schödinger equation:

via the Liouville transformation:

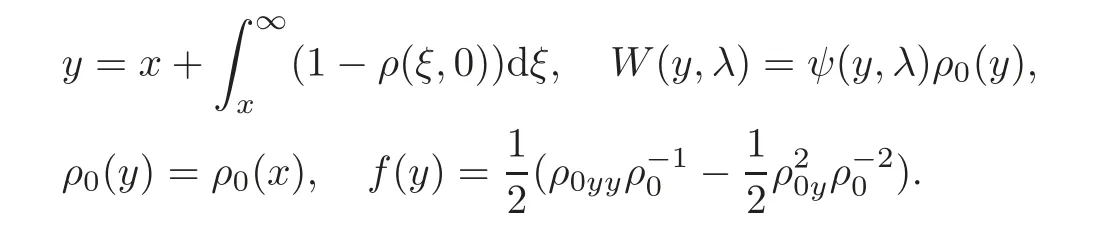
Therefore,in terms of the spectral problem of the Schrödinger equation,we deduce that a(λ)has only pure imaginary part of simple poles in the upper plane.

3 The Riemann-Hilbert Problem

3.1 A Riemann-Hilbert problem for(x,t)

We now solve the initial value problem for(2.1)on the line,and the solution can be expressed in terms of a 2×2 matrix Riemann-Hilbert problem.Let M(x,t,λ)be defined by

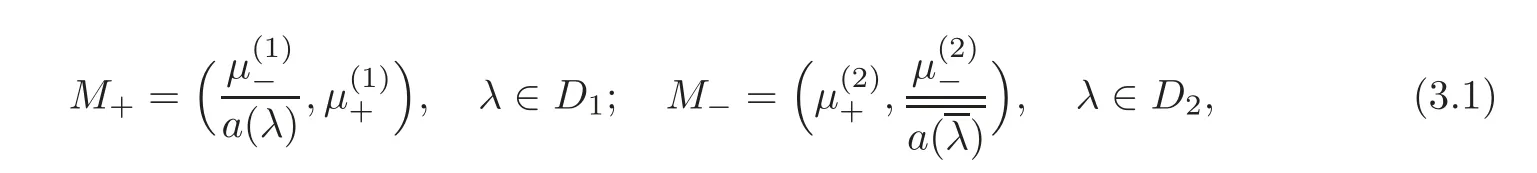
and let the M satisfy the jump condition:

where

These definitions imply

and

This contour of the Riemann-Hilbert problem is the real axis.

The jump matrix J(x,t,λ),and the spectral a(λ)and b(λ)are dependent on the y(x,t),while y(x,t)doesn’t involve initial data.Therefore,this Riemann-Hilbert problem can not be formulated in terms of initial data alone.In order to overcome this problem,we will reconstruct a new jump matrix by changing

where y is a new scale.Then we can transform this Riemann-Hilbert problem into the Riemann-Hilbert problem parametrized by(y,t).

3.2 A Riemann-Hilbert problem for(y,t)

Theorem 3.1 Let q0(x),x∈R be a smooth function and decay as|x|→ ∞.Moreover 1+q0(x)>0.Define the,ρ0and y0(x)as follows:

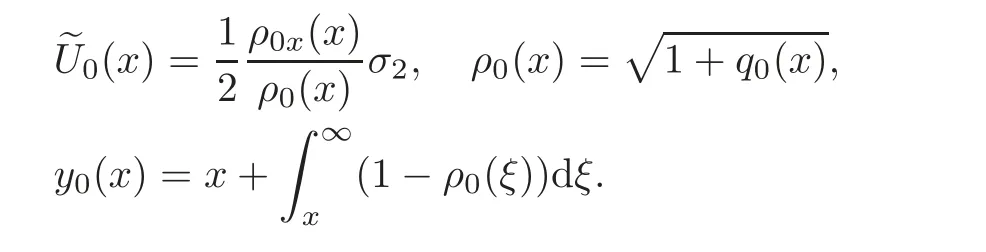
Let μ+(x,0,λ)and μ−(x,0,λ)be the unique solution of the Volterra linear integral equation(2.5)evaluated at t=0 withDe fine a(λ),b(λ),Cjby

and

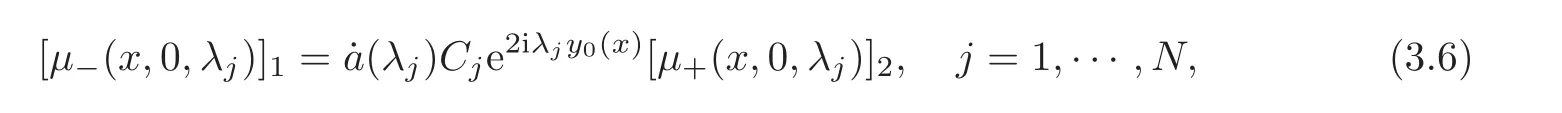
here and here after([A]1[A]2)denotes the first(second)column of a 2×2 matrix A.We assume that a(λ)has N simple zerosin the upper half plane and is pure imaginary.Then

(1)a(λ)is defined for k ∈and analytic in D1.

(2)b(λ)is defined for λ ∈ R.

(4)a(λ)=1+O,λ→∞,λ∈D1.

(5)b(λ)=O??,λ→∞,λ∈R.

Suppose that there exists a uniquely solution q(x,t)of(1.2)with initial data q0(x)such thathas sufficient smoothness and decays for t>0.Then q(x,t)is given in the parametric form by

and the function x(y,t)is defined by

where m(y,t)and M(y,t,λ)is the unique solution of the following Riemann-Hilbert problem:

(1)

is a sectionally meromorphic function.

(2)

where J(y)(y,t,λ)is defined by

(3)

(4)The possible simple poles of the first column of M+(y,t,λ)occur at λ = λj,j=1,···,N,and the possible simple poles of the second column of M−(y,t,λ)occur at λ =,j=1,···,N.The associated residues are given by

Proof Assume that μ(x,t)is the solution of equation(2.5),and its asymptotic expansion is

into the x-part of(2.5),where μ(1)(x,t), μ(2)(x,t)and μ(3)(x,t)are 2×2 matrices,dependent on x,t.By considering the terms of O(1),We get

By construction of the new Riemann-Hilbert problem about(y,t,λ),we can deduce that

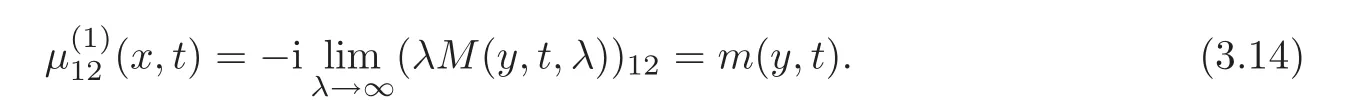
Then

(3.13)can be expressed in terms of y=y(x,t).Indeed,using=ρ,then(3.15)becomes

As|y|→ ∞,ρ(y,t)→ 1,by the evaluation of(3.16),we get

Therefore

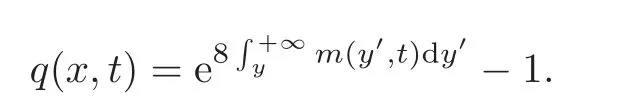
As|x|→ ∞,|y|→∞ and=ρ>0,

Remark 3.1 It follows from the symmetries(2.10)that the solution M(y,t,λ)of the Riemann-Hilbert problem in Theorem 3.1 has the symmetries:

4 Soliton Solution

The solitons correspond to the spectral data{a(λ),b(λ),Cj}for which b(λ)vanishes identically.In this case,the jump matrix J(y)(y,t,λ)in the(3.9)is the identity matrix and the Riemann-Hilbert problem of Theorem 3.1 consists of finding a meromorphic function M(y,t,λ)satisfying(3.10)and the residue conditions(3.11)–(3.12).From(3.10)–(3.11),we get

For the symmetries(3.17),(4.1)can be written as

Letbecomes

Solving this algebraic system for M12(y,t,λj),M22(y,t,λj),n=1,···,N,and substituting them into(4.1)provide an explicit expression for the[M(y,t,λ)]1.In terms of the symmetries(3.17),we can get M12(y,t,λ),which solves the Riemann-Hilbert problem.Then

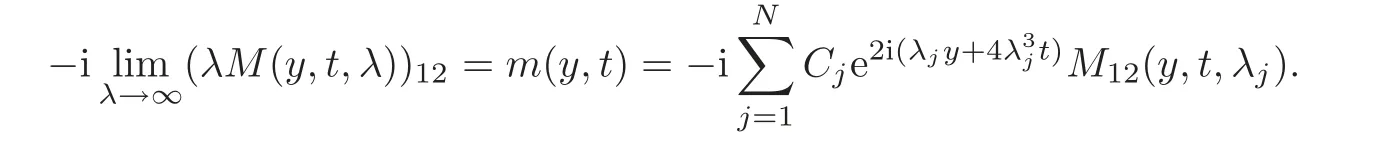
Therefore,the N soliton solution q(x,t)is expressed by the(3.7).

4.1 The one-soliton solution

In this section,we derive an explicit formula for the one-soliton solution,which arises when a(λ)has a pure imaginary λ1of simple zero.Letting N=1 in(4.3),from the the symmetries of(2.10),we can deduce thatand thenSince the b1is a real constant,wefind that C1=−C1,and thus C1is pure imaginary.Making use of the symmetries of(3.17),we can obtain

Then

Substituting this result into(4.3),we get

Let λ1=iε, ε >0,and in order to conveniently study the properties of the one soliton solution,we choose C1= ±2iε.When C1= −2iε,substituting both parameters into(4.4),it comes into being that

Then

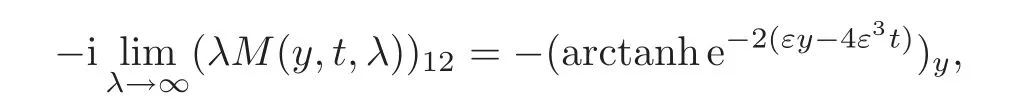
where the arctanhx is the inverse function of tanhx.Furthermore,

The solution q(x,t)in(3.7)can be transformed into

Letting α(y,t)=earctanhe−2(εy−4ε3t),wefind that Lnα(y,t)=arctanhe−2(εy−4ε3t),and then

i.e.,

We deduce

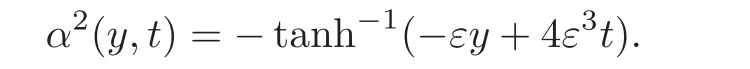
(4.7)can be written as

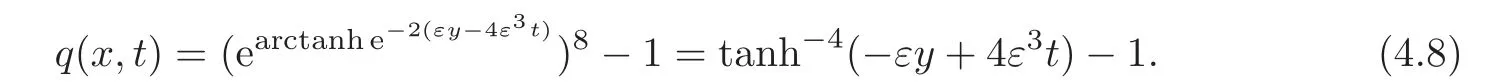
Substituting y with x,(4.8)becomes

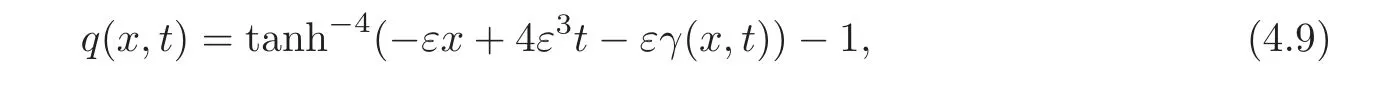
whereThen(4.9)can be varied as(1+q(x,t)−1=cosh2(−εx+4ε3t−εγ(x,t)),and hence the one soliton solution q(x,t)has a singularity at the peak of the soliton,the so-called cusp soliton.

When λ1=iε and C1=2iε,the corresponding one soliton solution q(x,t)of(1.2)can be expressed as

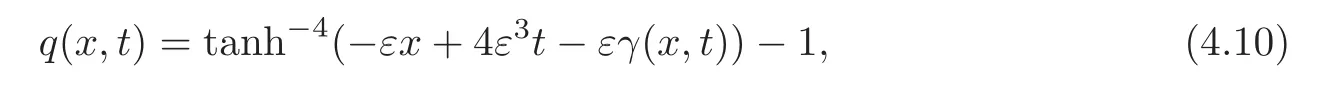
where

Remark 4.1 In this paper,we use the Riemann-Hilbert approach to obtain the solution q(x,t)of(1.2)expressed by(4.9)–(4.10).While[3]applies the inverse scattering method to get the solution q(x,t).If ε= κ (κ in[3],to the one soliton solution,when C1= −2iε,the expression of the solution in both papers is similar,identical with −εx+4ε3t in the

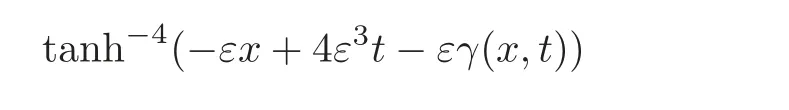
and κx−4κ3t in the tanh−4(κx−4κ3t−κx0+ε+)in[3]).There is a different point about the expression of the one soliton solution in the two papers,i.e.,one is dependent of the−εγ(x,t)of x and the other is−κx0+ε+of x.

[1]Hereman,W.,Banerjee,P.P.and Chatterjee,M.R.,Derivation and implicit solution of the Harry-Dym equation and its connections with the Korteweg-de Vries equation,J.Phys.A:Mat.Gen.,22,1989,241–255.

[2]Kadanoff,L.P.,Exact solutions for the Saffman-Taylor problem with surface tension,Phys.Rev.Lett.,65,1990,2986–1990.

[3]Wadati,M.and Yoshi,H.,Ichikawa and Toru Shinizu,Cusp soliton of a new integrable nonlinear evolution equation,Proc.Theor.Phys.,64,1980,1959–1967.

[4]Magri,F.,A geometrical approach to the nonlinear solvable equations,Nonlinear Evolution Equations and Dynamical Systems Lecture Notes in Physics,120,1980,233–263.

[5]Leo,M.,Leo,R.A.,Soliani,G.,et al.,Lie-Backlund symmetries for the Harry-Dym equation,Phys.Rev.D.,26,1980,1406–1407.

[6]Rogers,C.and Nucci,M.C.,On reciprocal Backlund transformations and the Korteweg-de Vries hierarchy,Phys.Scr.,33,1986,289–292.

[7]Leo,M.,Leo,R.A.,Soliani,G.and Solombrino,L.,On the isospectral-eigenvalue problem and the recursion operator of the Harry-Dym equation,Phys.Scr.,38,1983,45–51.

[8]Banerjeet,P.P.,Daoudt,F.and Hereman,W.,A straightforward method for finding implicit solitary wave solutions of nonlinear evolution and wave equations,J.Phys.A:Math.Gen.,23,1990,521–536.

[9]Lenells,J.and Fokas,A.S.,On a novel integrable generalization of the nonlinear Schrödinger equation,Nonlinearity,22,2009,11–27.

[10]Boutet de Monvel,A.and Shepelsky,D.,Riemann-Hilbert problem in the inverse scattering for the Camassa-Holm equation on the line,Math.Sci.Res.Inst.Publ.,55,2008,53–75.

[11]Boutet de Monvel,A.and Shepelsky,D.,A Riemann-Hilbert approach for the Degasperis-Procesi equation,Nonlinearity,26 2013,2081–2107.

[12]Fokas,A.S.,A unified transform method for solving linear and certain nonlinear PDEs,Proc.Roy.Soc.Lond.A,453,1997,1411–1443.

[13]Fokas,A.S.,On the integrability of linear and nonlinear partial differential equations,J.Math.Phys.,41,2000,4188–4237.

[14]Fokas,A.S.,A Unified Approach to Boundary Value Problem,CBMS-NSF Reginal Conference Series in Applied Mathematics,SIAM,2008.

[15]Lenells,J.and Fokas,A.S.,An integrable generalization of the nonlinear Schrödinger equation on the half-line and solitons,Inver.Prob.,25,2009,1–12.

[16]Fokas,A.S.and Lenells,J.,Explicit soliton asymptotics for the Korteweg-de Vries equation on the half-line,Nonlinearity,23,2010,937–976.

[17]Lenells,J.,An integrable generalization of the sineCGordon equation on the half-line,IMA J.Appl.Math.,76,2011,554–572.