Orientable Small Covers over a Product Space∗
2016-06-09DantingWANGYanyingWANGYanhongDING
Danting WANGYanying WANGYanhong DING
1 Introduction
The geometry of toric varieties is one of the fascinating topics in algebraic geometry and has found applications in many branches of mathematical sciences.From a combinatorial viewpoint,it is known that there is a one-to-one correspondence between fans in Rnand toric varieties of complex dimension n.Given an n-polytope Pnwith vertices in the integer lattice Zn,a fan is generated by the set of normal vectors corresponding to faces of codimension 1 of Pn.According to the above correspondence between fans and toric varieties,there is a toric variety MPassociated to the fan.Let Tndenote a torus(S1)n.It turns out that as a topological space,MP=Tn×Pn/∼for some equivalent relation∼.The torus Tnnaturally acts on MP,and Pnis the orbit space.Inspired by the above identification space description of a toric variety,Davis and Januszkiewicz introduced a topological counterpart,namely,the study of small covers and quasitoric manifolds in[5].
A small cover(see[5])is a closed manifold Mnwith a locally standard(Z2)n-action such that its orbit space is a simple convex polytope Pn,where Z2denotes the cyclic group of order 2.For instance,the real projective space RPnwith a natural(Z2)n-action is a small cover over an n-simplex.This makes the research on the equivariant topology of small covers possible through the combinatorial structure of the orbit space.
In[7],LÜ and Masuda showed that the equivariant homeomorphism class of a small cover over a simple convex polytope Pnagrees with the equivalent class of its corresponding char-acteristic functions under the action of the automorphism group of face poset(i.e.,a partially ordered set by inclusion)of Pn.This finding also holds true for orientable small covers by the orientability condition(see Theorem 2.2).However,it is a hard task to obtain general formulas for calculating the number of equivariant homeomorphism classes of(orientable)small covers over an arbitrary simple convex polytope.
In recent years,several studies have attempted to calculate the number of equivalent classes of all small covers over a specific polytope.Garrison and Scott used a computer program to calculate the number of homeomorphism classes of all small covers over a dodecahedron(see[6]).Cai,Chen and LÜ calculated the number of equivariant homeomorphism classes of small covers over prisms(see[2]).However,little is known about orientable small covers.Choi calculated the number of D-J equivalent classes of orientable small covers over cubes(see[4]).Chen and Wang calculated the number of equivariant homeomorphism classes of orientable small covers over a product of at most three simplices(see[3]).From[9],we know the existence of orientable small covers over the polytope Δn1× Δn2×P(m),where Δnidenotes a simplex of dimension niand P(m)an m-gon.The objective of this paper is to determine the number of D-J equivalent classes and equivariant homeomorphism classes of all orientable small covers over Δn1×Δn2×P(m),where n1is odd.
This paper is organized as follows.In Section 2,we review the fundamental knowledge on small covers and list several known theorems.In Section 3,we calculate the number of D-J equivalent classes of the orientable small covers over the product space and the number of orientable characteristic functions corresponding to orientable small covers.In Section 4 we obtain a formula for calculating the number of equivariant homeomorphism classes of all orientable small covers over the product space.
2 Preliminaries
The standard action of(Z2)non Rnis that

and the orbit space is={(x1,···,xn)∈ Rn|xi≥ 0,1 ≤ i≤ n}.
A convex polytope Pnof dimension n is said to be simple if every vertex of Pnis the intersection of exactly n facets(i.e.,faces of dimension(n−1))(see[10]).An n-dimensional closed manifold Mnis said to be a small cover if it admits a(Z2)n-action such that the action is locally isomorphic to a standard action of(Z2)non Rnand the orbit space Mn/(Z2)nis a simple convex polytope of dimension n(see[5]).
Let Pnbe a simple convex polytope of dimension n and F(Pn)={F1,···,Fl}be the set of facets of Pn.Suppose that π :Mn→Pnis a small cover over Pn.Then there are l connected submanifolds π−1(F1),···,π−1(Fl).Each submanifold π−1(Fi)is fixed pointwise by a subgroup Z2(Fi)of rank 1 in(Z2)n,so that each facet Ficorresponds to a subgroup Z2(Fi)of rank 1.Obviously,the subgroup Z2(Fi)actually agrees with an element νiin(Z2)nas a vector space.For each face F of codimension u of Pn,since Pnis simple,there are u facets Fi1,···,Fiusuch that F=Fi1∩ ···∩ Fiu.Then,the corresponding submanifolds π−1(Fi1),···,π−1(Fiu)intersect transversally in the(n − u)-dimensional submanifold π−1(F),and the isotropy subgroup Z2(F)of π−1(F)is generated by Z2(Fi1),···,Z2(Fiu)(or is determined by νi1,···,νiuin(Z2)n),and has rank u.Thus,this gives a function(see[5]):

which is defined by λ(Fi)= νi.This function satisfies the non-singularity condition:λ(Fi1),···,λ(Fiu)are linearly independent in(Z2)nas a vector space whenever the intersection Fi1∩ ···∩Fiuis non-empty.We call λ,which satisfies the non-singularity condition,a characteristic function on Pn.
In fact,Davis and Januszkiewicz[5]also gave a reconstruction process of a small cover using a characteristic function λ :F(Pn)→ (Z2)n.Let Z2(Fi)be the subgroup of(Z2)ngenerated by λ(Fi).Given a point p ∈ Pn,we denote the minimal face containing p in its relative interior by F(p).Assuming that F(p)=Fi1∩ ···∩ Fiuandthen Z2(F(p))is a subgroup of rank u in(Z2)n.Let M(λ)denote Pn×(Z2)n/∼,where(p,g)∼ (q,h)if p=q and g−1h ∈ Z2(F(p)).The free action of(Z2)non Pn× (Z2)ndescends to an action on M(λ)with quotient Pn.Thus,M(λ)is a small cover over Pn.
Two small covers M1and M2over Pnare said to be weakly equivariantly homeomorphic if there is an automorphism ϕ:(Z2)n→(Z2)nand a homeomorphism f:M1→M2such that f(t·x)= ϕ(t)·f(x)for every t∈ (Z2)nand x ∈ M1.If ϕ is an identity,then M1and M2are equivariantly homeomorphic.Following[5],two small covers M1and M2over Pnare said to be Davis-Januszkiewicz equivalent(or simply,D-J equivalent)if there is a weakly equivariant homeomorphism f:M1→M2covering the identity on Pn.
By Λ(Pn),we denote the set of characteristic functions on Pn.We have the following result.
Theorem 2.1(see[5])All small covers over Pnare given by{M(λ)|λ ∈ Λ(Pn)},i.e.,for each small cover Mnover Pn,there is a characteristic function λ with an equivariant homeomorphism M(λ)→ Mncovering the identity on Pn.
Nakayama and Nishimura gave an orientability condition for a small cover in[9].
Theorem 2.2(see[9])For a basis{e1,···,en}of(Z2)n,a homomorphism ε:(Z2)n→Z2={0,1}is defined by ε(ei)=1(i=1,···,n).A small cover M(λ)over a simple convex polytope Pnis orientable if and only if there exists a basis{e1,···,en}of(Z2)nsuch that the image of ελ is{1}.
From Theorem 2.2,we know that a small cover M(λ)over Pnis orientable if and only if there exists a basis{e1,···,en}of(Z2)nsuch that λ(Fi)=ei1+ei2+ ···+ei2hi+1,1 ≤i1 In order to classify orientable small covers over Pnup to D-J equivalence,by O(Pn)we denote the set of orientable characteristic functions on Pn,and consider a free action of GL(n,Z2)on O(Pn)defined by the correspondence σ × λ ?→ σ ◦ λ.We assume that F1,···,Fnof F(Pn)meet at one vertex p of Pn.Let e1,···,enbe the standard basis of(Z2)nand B(Pn)={λ ∈ O(Pn)|λ(Fi)=ei,i=1,···,n}.Then B(Pn)is the orbit space of O(Pn)under the action of GL(n,Z2).In fact,for λ∈B(Pn)and n+1≤i≤l,we have λ(Fi)=ei1+ei2+ ···+ei2hi+1,1 ≤ i1 Lemma 2.1 |O(Pn)|=|B(Pn)|×|GL(n,Z2)|. It is easy to check that two orientable small covers M(λ1)and M(λ2)over Pnare D-J equivalent if and only if there is σ ∈ GL(n,Z2)such that λ1= σ ◦ λ2.Thus the number of D-J equivalent classes of orientable small covers over Pnis|B(Pn)|=|O(Pn)|/|GL(n,Z2)|.From[1],we know For calculating the number of equivariant homeomorphism classes of orientable small covers over a simple convex polytope Pn,we consider a poset consisting of faces of Pn(i.e.,a partially ordered set by inclusion).An automorphism of F(Pn)is a bijection from F(Pn)to itself that preserves the poset structure of all faces of Pn.By Aut(F(Pn)),we denote the group of automorphisms of F(Pn).We define a right action of Aut(F(Pn))on O(Pn)by λ ×h?→ λ ◦h,where λ ∈ O(Pn)and h ∈ Aut(F(Pn)).By improving the classifying result on unoriented small covers in[7],we have the following theorem. Theorem 2.3 Two orientable small covers over an n-dimensional simple convex polytope Pnare equivariantly homeomorphic if and only if there is h ∈ Aut(F(Pn))such that λ1= λ2◦h,where λ1and λ2are their corresponding orientable characteristic functions on Pn. Proof It is proven true by combining Lemma 5.4 in[7]with Theorem 2.2. According to Theorem 2.3,the number of equivariant homeomorphism classes of orientable small covers over Pnis equal to the number of orbits of O(Pn)under the action of Aut(F(Pn)).The famous Burnside Lemma is very useful in enumerating the number of orbits. Lemma 2.2(Burnside Lemma)Let G be a finite group acting on a set X.Then the number of orbits under the action of G equals To determine the number of the orbits of O(Pn)under the action of Aut(F(Pn)),the Burnside Lemma suggests that the structure of Aut(F(Pn))should be understood. Here we shall particularly be concerned with the case Pn= Δn1×Δn2×P(m),where Δnidenotes a simplex of dimension niand P(m)an m-gon.In this case,by O(n1,n2,m),B(n1,n2,m),F(n1,n2,m)and Aut(F(n1,n2,m)),we denote O(Δn1×Δn2×P(m)),B(Δn1×Δn2×P(m)),F(Δn1×Δn2×P(m))and Aut(F(Δn1×Δn2×P(m)))respectively.Then we have the following lemma. Lemma 2.3(see[8])The automorphism group Aut(F(n1,n2,m))is isomorphic to where Dmis the dihedral group of order 2m and Sn+1is the symmetric group on n+1 symbols. Let{a1,···,an1,an1+1}be the set of facets of Δn1×Δn2×P(m)corresponding to F(Δn1)×Δn2×P(m),{b1,···,bn2,bn2+1}the set of facets corresponding to Δn1×F(Δn2)×P(m),and{c1,c2,···,cm}the set of facets corresponding to Δn1×Δn2×F(P(m))in their general order.Then F(n1,n2,m)={a1,···,an1,an1+1}∪{b1,···,bn2,bn2+1}∪{c1,c2,···,cm}.Without loss of generality,we assume that a1,···,an1,b1,···,bn2,c1and c2are facets of Δn1×Δn2×P(m)which meet at a vertex.Let e1,e2,···,en1+n2+2be the standard basis of(Z2)n1+n2+2.By definition, Let fi(n1,n2,m)be the recursive functions which are listed in Appendix 1.Now we arrive at the first main result. Theorem 3.1 Let n1,n2and m be positive integers,with n1odd,n1≥2,n2≥1,n1≥n2and m≥3.Then the number of D-J equivalent classes of orientable small covers over Δn1×Δn2×P(m)is where I1={1,2,···,24}and I2={8,12,17,19}. Proof By the non-singularity condition of orientable characteristic functions,we have where εi,δj=0 or 1,i=1,···,n2+2,j=1,···,n1+2,and withγi,θj,μp=0 or 1. The calculation of|B(n1,n2,m)|is divided into eight cases.Write Then|B(n1,n2,m)|Now we calculate|Bi(n1,n2,m)|(1≤i≤8). Case 1 Calculation (1) According to the non-singularity condition and the orientability condition of characteristic functions,the number ofδi=1 is even forn2odd,the number ofδi=1 is odd forn2even,and the coefficients inλ(cm)andλ(cm−1)are listed in Table 1. Table 1 Set Ifλthen the values ofλrestricted tocm−1have 2n1+n2−1possible choices and the values ofλrestricted tocmhave 2n1+n2possible choices.So,we obtain a recursive equation Ifλ∈thenλ(cm−1)has 2n1+n2−1possible values.We have|(n1,n2,m)|=2n1+n2−1|B11(n1,n2,m−1)|.So Sinceλ(bn2+1)has 2n1−1possible values,a direct computation shows that|B11(n1,n2,3)|=(2n1+n2−1)·2n1−1=22n1+n2−2,|B11(n1,n2,4)|=3·22n1+2n2−2·2n1−1=3·23n1+2n2−3.So A similar argument shows that the number ofδi=1 is odd forn2odd,the number ofδi=1 is even forn2even,and the coefficients inλ(cm)andλ(cm−1)are listed in Table 2. Table 2 Similarly,we have that the number ofδi=1 is odd forn2odd and the number ofδi=1 is even forn2even.The coefficientsγiandθjappear in Table 3. Table 3 The number ofδi=1 is even forn2odd and the number ofδi=1 is odd forn2even.The coefficientsγiandθjare in Table 4. Table 4 Thusf4(n1,n2,m). Case 2 Calculation of|B2(n1,n2,m)|. Ifn2is even,then Ifn2is odd,we consider the values ofλ(cm)andλ(cm−1)listed in Table 5. Table 5 We get|B21(n1,n2,m)|=2n1+n2−1|B21(n1,n2,m−1)|+22n1+2n2−1|B21(n1,n2,m−2)|,|B21(n1,n2,3)|=2n1+2n2−2−2n1+n2−1and|B21(n1,n2,4)|=3·22n1+3n2−3−3·22n1+2n2−2.Sof5(n1,n2,m)=|B21(n1,n2,m)|. (2) Ifn2is odd,then|B22(n1,n2,m)|=0.Ifn2is even,we consider the values ofλ(cm)andλ(cm−1)in Table 6. Table 6 Ifn2is odd,then|B23(n1,n2,m)|=0.Ifn2is even,we consider the values ofλ(cm)andλ(cm−1)in Table 7. Ifn2is even,then|B24(n1,n2,m)|=0.Ifn2is odd,thenλ(cm)=en1+n2+2,λ(cm−1)=en1+n2+1.Thus|B24(n1,n2,m)|=|B24(n1,n2,m−2)|,|B24(n1,n2,3)|=0 and|B24(n1,n2,4)|=2n2−1−1.Sof8(n1,n2,m)=|B24(n1,n2,m)|. Thusf8(n1,n2,m). Case 3 Calculation of|B3(n1,n2,m)|. Becausen1is odd,|B3(n1,n2,m)|=0. Case 4 Calculation of|B4(n1,n2,m)|. Ifn2is even,then|B41(n1,n2,m)|=0.Ifn2is odd,thenλ(cm)andλ(cm−1)have the possible values in Table 8. Table 8 Sof9(n1,n2,m)=|B41(n1,n2,m)|. Ifn2is odd,then|B42(n1,n2,m)|=0.Ifn2is even,thenλ(cm)andλ(cm−1)have the possible values in Table 9. Table 9 We get|B42(n1,n2,m)|=2n1+n2|B42(n1,n2,m−2)|,|B42(n1,n2,3)|=2n1+2n2−2and|B42(n1,n2,4)|=2n1+2n2−1.Sof10(n1,n2,m)=|B42(n1,n2,m)|. Table 10 Ifn2is odd,then|B43(n1,n2,m)|=0.Ifn2is even,thenλ(cm)andλ(cm−1)have the possible values in Table 10. We have|B43(n1,n2,m)|=2n2|B43(n1,n2,m−2)|,|B43(n1,n2,3)|=0 and|B43(n1,n2,4)|=22n2−1.Sof11(n1,n2,m)=|B43(n1,n2,m)|. Ifn2is even,then|B44(n1,n2,m)|=0.Ifn2is odd,thenλ(cm)=en1+n2+2,λ(cm−1)=en1+n2+1.We have|B44(n1,n2,m)|=|B44(n1,n2,m−2)|,|B44(n1,n2,3)|=0 and|B44(n1,n2,4)|=2n2−1.Sof12(n1,n2,m)=|B44(n1,n2,m)|. Thusf12(n1,n2,m). Case 5 Calculation of|B5(n1,n2,m)|. Becausen1is odd,|B5(n1,n2,m)|=0. Case 6 Calculation of|B6(n1,n2,m)|. In this case,the number ofεi=1 is odd. Ifn2is even,then|B61(n1,n2,m)|=0.Ifn2is odd,thenλ(cm)andλ(cm−1)have the possible values in Table 11. Table 11 Leten1+n2+1+en1+n2+2(∃θi?=0,1≤i≤n1),and(n1,n2,m)=B61(n1,n2,m)(n1,n2,m).We have|(n1,n2,m)|=2n1+2n2−1|B61(n1,n2,m−2)|and|(n1,n2,m)|=2n2−1|B61(n1,n2,m−1)|.Then|B61(n1,n2,m)|=2n2−1|B61(n1,n2,m−1)|+2n1+2n2−1|B61(n1,n2,m−2)|,|B61(n1,n2,3)|=22n2−2and|B61(n1,n2,4)|=2n1+3n2−2+23n2−3.Sof13(n1,n2,m)=|B61(n1,n2,m)|. Table 12 (2) Ifn2is odd,then|B62(n1,n2,m)|=0.Ifn2is even,thenλ(cm)andλ(cm−1)have the possible values in Table 12. We get|B62(n1,n2,m)|=2n2|B62(n1,n2,m−2)|,|B62(n1,n2,3)|=22n2−2and|B62(n1,n2,4)|=22n2−1.Sof14(n1,n2,m)=|B62(n1,n2,m)|. Ifn2is odd,then|B63(n1,n2,m)|=0.Ifn2is even,thenλ(cm)andλ(cm−1)have the possible values in Table 13. Table 13 We have|B63(n1,n2,m)|=2n1+n2|B63(n1,n2,m−2)|,|B63(n1,n2,3)|=0 and|B63(n1,n2,4)|=2n1+2n2−1.Sof15(n1,n2,m)=|B43(n1,n2,m)|. Ifn2is even,then|B64(n1,n2,m)|=0.Ifn2is odd,thenλ(cm)=en1+n2+2,λ(cm−1)=en1+n2+1.So,|B64(n1,n2,m)|=|B64(n1,n2,m−2)|,|B64(n1,n2,3)|=0 and|B64(n1,n2,4)|=2n2−1.By definition,f12(n1,n2,m)=|B64(n1,n2,m)|. Thus|+f12(n1,n2,m). Case 7 Calculation of|B7(n1,n2,m)|. Ifn2is even,then|B71(n1,n2,m)|=0.Ifn2is odd,thenλ(cm)andλ(cm−1)have the possible values in Table 14. Table 14 Leten1+n2+2(∃θi?=0,1≤i≤n1),and(n1,n2,m)=B71(n1,n2,m)(n1,n2,m).We have|(n1,n2,m)|=2n1+2n2−1|B71(n1,n2,m−2)|and|n1,n2,m)|=2n2−1|B71(n1,n2,m−1)|.Then|B71(n1,n2,m)|=2n2−1|B71(n1,n2,m−1)|+2n1+2n2−1|B71(n1,n2,m−2)|,|B71(n1,n2,3)|=2n2−1,and|B71(n1,n2,4)|=2n1+2n2−2+22n2−1.Sof16(n1,n2,m)=|B71(n1,n2,m)|. The number ofδi=1 is even forn2odd,and the number ofδi=1 is odd forn2even.λ(cm)=en1+n2+2,λ(cm−1)=en1+n2+1.We have|B72(n1,n2,m)|=|B72(n1,n2,m−2)|and|B72(n1,n2,3)|=0.Note that|B72(n1,n2,4)|=2n1−1−1 forn2odd,and|B72(n1,n2,4)|=2n1−1forn2even.Sof17(n1,n2,m)=|B72(n1,n2,m)|. Ifn2is odd,then|B73(n1,n2,m)|=0.Ifn2is even,thenλ(cm)andλ(cm−1)have the possible values in Table 15. Table 15 We have|B73(n1,n2,m)|=2n2|B73(n1,n2,m−2)|,|B73(n1,n2,3)|=2n2−1and|B73(n1,n2,4)|=2n2.Sof18(n1,n2,m)=|B73(n1,n2,m)|. The number ofδi=1 is odd forn2odd,and the number ofδi=1 is even forn2even.λ(cm)=en1+n2+2,λ(cm−1)=en1+n2+1.So,|B74(n1,n2,m)|=|B74(n1,n2,m−2)|,and|B74(n1,n2,3)|=0.Note that|B74(n1,n2,4)|=2n1−1forn2odd,and|B74(n1,n2,4)|=2n1−1−1 forn2even.Sof19(n1,n2,m)=|B74(n1,n2,m)|. Ifn2is odd,then|B75(n1,n2,m)|=0.Ifn2is even,thenλ(cm)andλ(cm−1)have the possible values in Table 16.We have|B75(n1,n2,m)|=2n2|B75(n1,n2,m−2)|,|B75(n1,n2,3)|=0,and|B75(n1,n2,4)|=2n2.Sof20(n1,n2,m)=|B75(n1,n2,m)|. Table 16 The number ofδi=1 is odd forn2odd,and the number ofδi=1 is even forn2even.λ(cm)=en1+n2+2,λ(cm−1)=en1+n2+1.We have|B76(n1,n2,m)|=|B76(n1,n2,m−2)|and|B76(n1,n2,3)|=0.Note that|B76(n1,n2,4)|=2n1−1forn2odd,and|B76(n1,n2,4)|=2n1−1−1 forn2even.By definition,f19(n1,n2,m)=|B76(n1,n2,m)|. Ifn2is even,then|B77(n1,n2,m)|=0.Ifn2is odd,thenλ(cm)=en1+n2+2,λ(cm−1)=en1+n2+1.So|B77(n1,n2,m)|=|B77(n1,n2,m−2)|,|B77(n1,n2,3)|=0,and|B77(n1,n2,4)|=1.Sof21(n1,n2,m)=|B77(n1,n2,m)|. The number ofδi=1 is even forn2odd,and the number ofδi=1 is odd forn2even.λ(cm)=en1+n2+2,λ(cm−1)=en1+n2+1.So,|B78(n1,n2,m)|=|B78(n1,n2,m−2)|and|B78(n1,n2,3)|=0.Note that|B78(n1,n2,4)|=2n1−1−1 forn2odd,and|B78(n1,n2,4)|=2n1−1forn2even.By definition,f17(n1,n2,m)=|B78(n1,n2,m)|. So,2f19(n1,n2,m)+f20(n1,n2,m)+f21(n1,n2,m). Case 8 Calculation of|B8(n1,n2,m)|. The number ofεi=1 is even. Ifn2is even,then|B81(n1,n2,m)|=0.Ifn2is odd,thenλ(cm)andλ(cm−1)have the possible values in Table 17. Table 17 Leten1+n2+2(∃θi?=0,1≤i≤n1)and(n1,n2,m)=B81(n1,n2,m)(n1,n2,m).We have(n1,n2,m)|=2n1+2n2−1|B81(n1,n2,m−2)|and|(n1,n2,m)|=2n2−1|B81(n1,n2,m−1)|.Thus|B81(n1,n2,m)|=2n2−1|B81(n1,n2,m−1)|+2n1+2n2−1|B81(n1,n2,m−2)|,|B81(n1, Ifn2is odd,then|B82(n1,n2,m)|=0.Ifn2is even,thenλ(cm)andλ(cm−1)have the possible values in Table 18. Table 18 We have|B82(n1,n2,m)|=2n2|B82(n1,n2,m−2)|,|B82(n1,n2,3)|=22n2−2−2n2−1and|B82(n1,n2,4)|=22n2−1−2n2.Sof23(n1,n2,m)=|B82(n1,n2,m)|. Ifn2is odd,then|B83(n1,n2,m)|=0.Ifn2is even,thenλ(cm)andλ(cm−1)have the possible values in Table 19. Table 19 Then|B83(n1,n2,m)|=2n2|B83(n1,n2,m−2)|,|B83(n1,n2,3)|=0 and|B83(n1,n2,4)|=22n2−1−2n2.Sof24(n1,n2,m)=|B83(n1,n2,m)|. Ifn2is even,then|B84(n1,n2,m)|=0.Ifn2is odd,thenλ(cm)=en1+n2+2,λ(cm−1)=en1+n2+1.We have|B84(n1,n2,m)|=|B84(n1,n2,m−2)|,|B84(n1,n2,3)|=0 and|B84(n1,n2,4)|=2n2−1−1.By definition,f8(n1,n2,m)=|B84(n1,n2,m)|. So,f8(n1,n2,m). whereI1={1,2,···,24}andI2={8,12,17,19}. The proof is completed. Remark 3.1 A direct calculation shows that|B(3,1,3)|=106. Theorem 3.2Suppose n1is odd,n1≥2,n2≥1,n1≥n2and m≥3.Then the number of orientable characteristic functions onΔn1×Δn2×P(m)is where I1={1,2,···,24}and I2={8,12,17,19}. Proof By Lemma 2.1 and Theorem 3.1,we have whereI1={1,2,···,24}andI2={8,12,17,19}. In this section,we determine the number of equivariant homeomorphism classes of all orientable small covers over Δn1×Δn2×P(m),which is denoted byEo(n1,n2,m). Letϕdenote the Euler’s totient function,that is,ϕ(1)=1 andϕ(N)for a positive integerN(N≥2)is the number of positive integers both less thanNand coprime toN.Recursive functions fi(n1,n2,m),gi(n1,m)and ki(n1,n2,m)are listed in the appendixes.Then we have the following theorem. Theorem 4.1 Suppose that n1is odd,n1≥2,n2≥1,m≥3 and n1≥n2,then the number of equivariant homeomorphism classes of orientable small covers over Δn1×Δn2×P(m)is (1)for n1>2,n2=1 and m=3 or n1≥2,n2=1 and m>4, where I1={1,2,···,24},I2={5,8,9,12,13,16,17,19,22}and I3={2,3,4}; (2)for n1≥2,n2=1 and m=4, where I1={1,2,···,24},I2={5,8,9,12,13,16,17,19,22}and I3={2,3,4}; (3)for n1>n2=2 and m>3 or n1>n2>2 and m≥3, where I1={1,2,···,24}and I2={8,12,17,19}; (4)for n1>n2=2 and m=3 or n1=n2>2 and m≥3, where I1={1,2,···,24}and I2={8,12,17,19}. Proof According to Theorem 2.3,Lemma 2.1 and Burnside Lemma,we have where Og={λ∈O(n1,n2,m)|λ=λ◦g}. In order to determine|Og|for g∈Aut(F(n1,n2,m)),we exhibit a system of generators of the group Aut(F(n1,n2,m)). Let x,y,si(i=1,···,n1),tj(j=1,···,n2)and zk(k=1,2,3,4)be the elememts of Aut(F(n1,n2,m))with the following properties: (1)x(ci)=ci+1(i=1,2,···,m − 1),x(cm)=c1,x(aj)=aj(j=1,2,···,n1+1)and x(bk)=bk(k=1,2,···,n2+1). (2)y(ci)=cm+1−i(i=1,2,···,m),y(cm)=c1,y(aj)=aj(j=1,2,···,n1+1)and y(bk)=bk(k=1,2,···,n2+1). (3)si(a1)=ai+1,si(ai+1)=a1,si(ap)=ap(p?=1,i+1),i=1,···,n1,si(bj)=bj(j=1,···,n2+1)and si(ck)=ck(k=1,···,m). (4)ti(b1)=bi+1,ti(bi+1)=b1,ti(bq)=bq(q?=1,i+1),i=1,···,n2,ti(aj)=aj(j=1,···,n1+1)and ti(ck)=ck(k=1,···,m). (5)z1(ai)=bi,z1(bi)=ai(i=1,···,n1+1)and z1(ck)=ck(k=1,···,m)if n1=n2. (6)z2(bi)=ci,z2(ci)=bi,and z2(ak)=ak(k=1,···,n1+1)if n2=2 and m=3. (7)z3(ai)=ci,z3(ci)=ai(i=1,2,3)and z3(bi)=bi(i=1,2)if n1=2,n2=1 and m=3. (8)z4(b1)=c1,z4(c1)=b1,z4(b2)=c3,z4(c3)=b2,z4(c2)=c2,z4(c4)=c4and z4(ak)=ak(k=1,···,n1+1)for n1≥ 2,n2=1 and m=4. Every g ∈ Aut(F(n1,n2,m))can be expressed in the form xuyv(?zi)w(?si)α(?tj)β,u ∈ Zm,v,w,α and β ∈ Z2.The calculation of|Og|is divided into the following cases. Case 1 n1>2,n2=1,and m=3 or n1≥2,n2=1 and m>4. According to Lemma 2.3,Aut(F(n1,n2,m))=Sn1+1×Z2×Dmand g∈Aut(F(n1,n2,m))can be written in the formwhere u ∈ Zm,v,w and α ∈ Z2. Subcase 1.1 g=xu. Let k=gcd(u,m)(i.e.,the greatest common divisor of u and m).Then all facets in F(n1,n2,m)are divided into k orbits under the action of g and each orbit containsfacets.This means k?=1.An argument similar to that of|Bi(n1,n2,m)|shows that|Og|=|O(n1,1,k)|where I1={1,2,···,24}and I2={8,12,17,19}.For every k>1,there are exactly ϕautomorphisms of the form xu,each of which divides all facets in F(n1,n2,m)into k orbits.Thus where I1={1,2,···,24}and I2={8,12,17,19}. Subcase 1.2 g=xut1. In this case,λ(b1)= λ(b2)for λ ∈ Og.An argument similar to that of|Bi(n1,n2,m)|shows Subcase 1.3 g=xuy,xuyt1,where m is odd,or u and m are even. If λ ∈ Og,then λ restricted to some adjacent facets has the same value,which contradicts the non-singularity condition.So|Og|=0. Subcase 1.4 g=xuy,where u is odd and m is even. Because|Og1|=|Og2|for g1,g2∈ Og,suppose g=xm−1y(i.e.,g=yx).Similarly to the proof of Theorem 3.1,let Xi(n1,1,m)={λ |λ ∈ Bi(n1,1,m),λ(cj)= λ(cm−j),m is even,and j=1,···,m − 1},where i=1,···,8.It is easy to show|X2(n1,1,m)|=|X3(n1,1,m)|=|X5(n1,1,m)|=|X8(n1,1,m)|=0. (1)Calculation of|X1(n1,1,m)|. Let X1i(n1,1,m)={λ |λ ∈ B1i(n1,1,m),λ(cj)= λ(cm−j),j=1,···,m−1},i=1,2,3,4.We have|X11(n1,1,m)|=2n1|X11(n1,1,m−2)|+22n1+1|X11(n1,1,m−4)|.|X11(n1,1,8)|=24n1+2,|X11(n1,1,6)|=23n1+1.So g1(n1,m)=|X11(n1,1,m)|. Similarly,|X12(n1,1,m)|=2n1−1|X12(n1,1,m−2)|+22n1|X12(n1,1,m−4)|.|X12(n1,1,8)|=24n1,|X12(n1,1,6)|=23n1.So g2(n1,m)=|X12(n1,1,m)|. |X13(n1,1,m)|=2n1−1|X13(n1,1,m−2)|+22n1|X13(n1,1,m−4)|.|X13(n1,1,8)|=3·24n1−1,|X13(n1,1,6)|=23n1.So g3(n1,m)=|X13(n1,1,m)|. |X14(n1,1,m)|=2n1−1|X14(n1,1,m−2)|+22n1|X14(n1,1,m−4)|.|X14(n1,1,8)|=3·24n1−2,|X14(n1,1,6)|=23n1−1.So g4(n1,m)=|X14(n1,1,m)|. (2)Calculation of|X4(n1,1,m)|. Let X4i(n1,1,m)={λ |λ ∈ B4i(n1,1,m),λ(cj)= λ(cm−j),j=1,···,m−1},i=1,2,3,4.Then So (3)Calculation of|X6(n1,1,m)|. Let X6i(n1,1,m)={λ |λ ∈ B6i(n1,1,m),λ(cj)= λ(cm−j),j=1,···,m−1},i=1,2,3,4.Then So|X6(n1,1,m)|=|X64(n1,1,m)|=g5(n1,m). (4)Calculation of|X7(n1,1,m)|. Let X7i(n1,1,m)={λ |λ ∈ B7i(n1,1,m),λ(cj)= λ(cm−j),j=1,···,m−1},i=1,···,8.Then By Burnside Lemma, Subcase 1.5 g=xuyt1,where u is odd and m is even. If λ ∈ Og,then λ(b1)= λ(b2).A similar argument as in subcase 1.4 shows Subcase 1.6 By the non-singularity condition,|Og|=0. From Burnside Lemma and|Aut(F(n1,n2,m))|=(n1+1)!4m,we get where I1={1,2,···,24},I2={5,8,9,12,13,16,17,19,22}and I3={2,3,4}. Case 2 n1≥2,n2=1 and m=4. According to Lemma 2.3,Aut(F(n1,1,4))=Sn1+1×(Z2)3×S3.g∈Aut(F(n1,1,4))can be written in the form,where u ∈ Zm,v,α,β and γ ∈ Z2. Subcase 2.1where α =1 or γ =1. By the non-singularity condition,|Og|=0. Subcase 2.2 The calculation is similar to the subcases 1.1–1.5.We omit the details.So where I1={1,2,···,24},I2={5,8,9,12,13,16,17,19,22}and I3={2,3,4}. Case 3 n1>n2>2 and m≥3,or n1>n2=2 and m>3. According to Lemma 2.3,Aut(F(n1,n2,m))=Sn1+1×Sn2+1×Dm.g∈Aut(F(n1,n2,m))can be written in the formwhere u ∈ Zm,v,α and β ∈ Z2. Subcase 3.1 g=xu. By an argument similar to that of the subcase 1.1,we have where I1={1,2,···,24}and I2={8,12,17,19}. Subcase 3.2 g=xuy,where m is odd,or u and m are both even. By the non-singularity condition,|Og|=0. Subcase 3.3 g=xuy,where u is odd and m is even. Without loss of generality,suppose g=xm−1y(i.e.,g=yx).Similar to the discussion in the subcase 1.4,let Xi(n1,n2,m)={λ |λ ∈ Bi(n1,n2,m),λ(cj)= λ(cm−j),j=1,···,m−1},where i=1,···,8.It is easy to show|X3(n1,n2,m)|=|X5(n1,n2,m)|=0. (1)Calculation of|X1(n1,n2,m)|. Let X1i(n1,n2,m)={λ | λ ∈ B1i(n1,n2,m),λ(cj)= λ(cm−j),j=1,···,m − 1},i=1,2,3,4.We have the following result. where I1={1,2,···,24}and I2={8,12,17,19}. By Burnside Lemma, where I1={1,2,···,24}and I2={8,12,17,19}. Subcase 3.4 g=where α =1 or β =1. By the non-singularity condition,|Og|=0. From Burnside Lemma,we get where I1={1,2,···,24}and I2={8,12,17,19}. Case 4 n1>n2=2 and m=3 or n1=n2>2 and m≥3. According to Lemma 2.3,Aut(F(n1,n2,m))=Sn1+1×Sn2+1×Z2×Dm.g∈Aut(F(n1,n2,m))can be written in the formwhere u ∈ Zm,v,α,β and γ ∈ Z2. Subcase 4.1 g=where α =1 or β =1 or γ =1. By the non-singularity condition,|Og|=0. Subcase 4.2 g=xu,xuy. The calculation is similar to the subcases 3.1–3.3.We omit the details.So where I1={1,2,···,24}and I2={8,12,17,19}. The proof is completed. Remark 4.1 A direct calculation shows that Eo(3,1,3)=8679444480. Appendix 1 Suppose that n1is odd,n1≥2,n2≥1,n1≥n2and m≥2.We list recursive functions fias follows: Appendix 2 Suppose positive integers n1≥2 and m≥3.We list recursive functions gi. Form odd,gi(n1,m)=0(1≤i≤7).For m even,giis defined as follows: Appendix 3 Suppose positive integers n1≥2,n2≥1 and m≥3.We list recursive functions ki. For m odd,ki(n1,n2,m)=0(1≤i≤24).For m even,kiis defined as follows: AcknowledgementThe authors would like to thank the referees for their very careful reading of the manuscript and valuable comments. [1]Alperin,J.L.and Bell,R.B.,Groups and Representations,Springer-Verlag,Berlin,1995. [2]Cai,M.,Chen,X.and LÜ,Z.,Small covers over prisms,Topology Appl.,154,2007,2228–2234. [3]Chen,Y.and Wang,Y.,Small covers over a product of simplices,Filomat,27,2013,777–787. [4]Choi,S.,The number of orientable small covers over cubes,Proc.Japan Acad.,Ser.A,86,2010,97–100. [5]Davis,M.and Januszkiewicz,T.,Convex polytopes,Coxeter orbifolds and torus actions,Duke Math.J.,62,1991,417–451. [6]Garrison,A.and Scott,R.,Small covers of the dodecahedron and the 120-cell,Proc.Amer.Math.Soc.,131,2003,963–971. [7]LÜ,Z.and Masuda,M.,Equivariant classification of 2-torus manifolds,Colloq.Math.,115,2009,171–188. [8]Meng,Y.,On closed manifolds and moment-angle complex in toric topology,Dissertation,Hebei Normal Univ.,2012. [9]Nakayama,H.and Nishimura,Y.,The orientability of small covers and coloring simple polytopes,Osaka J.Math.,42,2005,243–256. [10]Ziegler,G.M.,Lectures on Polytopes,Springer-Verlag,Berlin,1994.
3 D-J Equivalent Classes and Orientable Characteristic Functions






















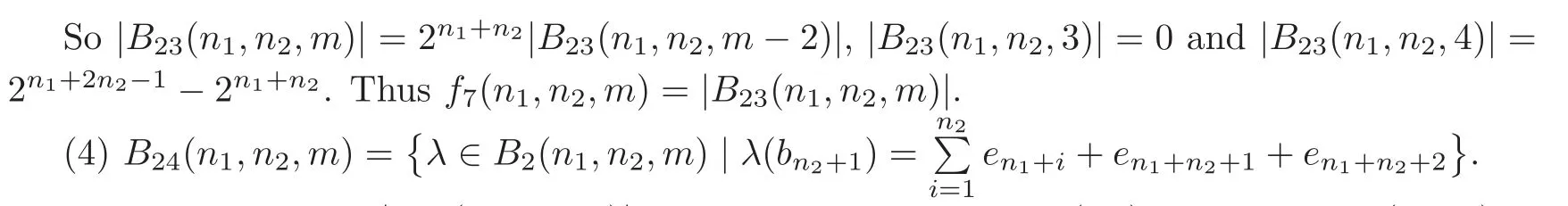

















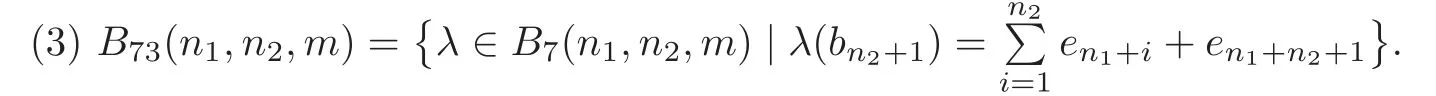


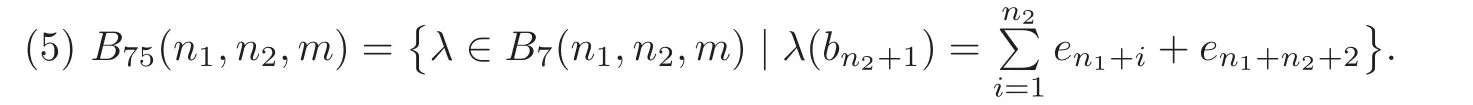










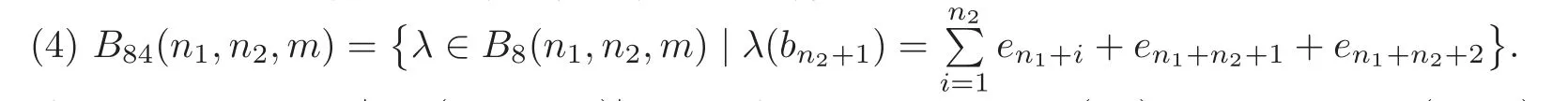



4 Equivariant Homeomorphism Classes



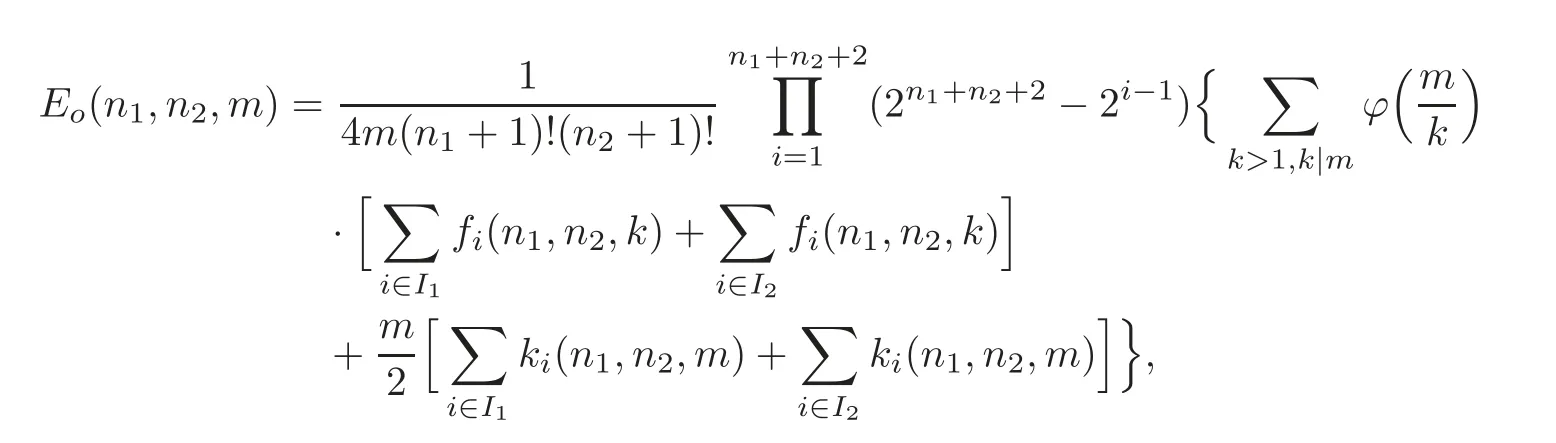
























杂志排行
Chinese Annals of Mathematics,Series B的其它文章
- Musical Isomorphisms and Problems of Lifts∗
- Canonical Metrics on Generalized Cartan-Hartogs Domains∗
- The(∗∗)-Haagerup Property for C∗-Algebras∗
- A Riemann-Hilbert Approach to the Harry-Dym Equation on the Line∗
- Embedding Generalized Petersen Graph in Books∗
- The Expansion of a Wedge of Gas into Vacuum with Small Angle in Two-Dimensional Isothermal Flow∗
